Original Article
, Volume: 13( 4)Temperature Dependent Dehydration Kinetics and Effective Diffusivity of Spinach Leaves
- *Correspondence:
- Prasad K
Department of Food Engineering and Technology, Sant Longowal Institute of Engineering and Technology, Longowal-148 106, Punjab, India
Tel: +91 1672- 253250; E-mail: profkprasad@gmail.com
Received Date: April 19, 2017 Accepted Date: July 02, 2017 Published Date: July 06, 2017
Citation: Prasad K, Ankita P. Temperature Dependent Dehydration Kinetics and Effective Diffusivity of Spinach Leaves. Biotechnol Ind J. 2017;13(4):142.
Abstract
The drying of spinach leaves was investigated in a laboratory dryer maintained at different isothermal temperatures ranging from 50°C to 90°C with an interval of 10°C. The effect of blanching and dehydration temperature on drying time and drying rate was studied. It was found that the dehydration kinetics of spinach leaves is temperature dependent and blanching has affected the dehydration characteristics. To an extent of 60% shortening of drying time has been found to yield the dehydrated leaves when dried at 80°C as compared to 50°C. Double stage drying of fresh spinach leaf is suggested with one hour initial drying at 80°C with the finishing the dehydration with 60°C further to obtain the quality dehydrated produce. Fitting of basic dehydration model confirmed the applicability of Page model in predicting the dehydration kinetics effectively. Effective moisture diffusivity was found to be temperature dependent and varied in the range 1.380 × 10-11 to 4.720 × 10-10 m2/s and 2.204 × 10-11 to 4.303 × 10-10 m2/s over considered dehydration range of temperature for untreated and blanched spinach leaves, respectively. The temperature dependence effective moisture diffusivity in form of activation energy was found to be 39.74 kJ/mol for untreated and 19.23 kJ/mol for blanched spinach.
Keywords
Spinach; Dehydration; Kinetics; Diffusivity; Model fitting
Introduction
Spinach (Spinacia oleracea L) is an herbaceous, annual and widely cultivated winter leafy vegetable. It is commonly known as Palak in India. The premium quality spinach leaves are basically harvested before the emergence of floral stalk. Leaves after harvesting still respire and transpire. Like most of the leaves, the spinach leaf is also thin, dorsi-ventral flattened like a thin slab thus having ample of exposed surface area per unit volume available for the transpiration, which results in rapid loss of leaf crispiness, depending on the extent of available environmental stress. Therefore, suggested to chill the spinach leaves immediately upon harvesting and store preferably more than 95% relative humidity. Otherwise, reduction in moisture leads to loss of leaf turgidity and acceptability thereof. Thus, most of the agricultural produce sold in the fresh form in India fetches low return to the farmers. As vegetable, spinach is low in calories and fat; good source of fiber with rich source of minerals (iron, calcium, magnesium, phosphorus, sodium, zinc and potassium) and vitamins (Vitamins A, B-complex, C and E) [1,2]. Moreover, this nutritious leafy vegetable is highly seasonal in nature and available at cheaper rate during the glut season. Inadequate processing and handling facilities in India witnessed the huge loss of fresh vegetables and in the tune of 5-50% or even higher [3]. Dehydration is thus a suitable alternative as post-harvest management especially in the developing countries like India, where the existence of poorly established facilities of cold chain [4-6]. Over 20% of the world perishable crops are being dehydrated to improve the shelf life and to promote the food security [7,8].
Chlorophyll is the derivative of dihydroporphyrin, chelated with centrally located magnesium atom responsible for green coloration and photosynthesis of leaves. The activation of chlorophyllase enzyme is found to be temperature dependent (60 - 82.2°C) to convert chlorophyll into chlorophylidine a bright green pigment [9], which is relatively more thermal resistant. The subsequent reductions in moisture content during the process of dehydration especially during the falling rate period raises the temperature and reduces moisture content further and arrests the mobility of reacting entities and thus arrest further conversion of chlorophyll as well as phyllin to maintain the green color intact. Further, prolonged exposure to higher temperature favours the formation of brown discolouration of leaves through non enzymatic pathway [10]. Blanching, a preprocessing unit operation, one of the mild heat treatment provided to vegetable in order to inactivate the responsible enzymes deteriorating the quality. Other associated benefits of blanching are retention and fixation of color, softening the vegetative tissues; texture modification; removal of objectionable flavor and removal of occluded air to facilitate the quality retention in processed foods prepared by applying different preservation principles. The loss of soluble solids in hot water blanching restricts its wider application. Steam blanching thus proves to be the effective method of blanching but softening of leaf like material further limit the use mainly due to separation and spreading of blanched leaves for thin layer drying to get uniform dehydration and dehydrated product characteristics. Although research findings prove the rapid initial dehydration rate of blanched vegetables but results in higher shrinkage with more moisture in final dehydrated mass then counterpart.
Dehydration is a classical and complex processing technique employing simultaneous heat and mass transfer to get solid food product with extended shelf life. Data of moisture loss with respect to time has been found important to describe the inherent phenomenon during the drying kinetics study. The process of moisture migration in form of molecule, liquid and vapor is basically controlled by diffusion phenomenon. The vegetable leaves are generally dried at 80°C until the moisture content goes below 6.5% [11]. The in-depth process understanding thus help in depicting the applicability of transcendental model to engineer the dehydration process with the improved process efficiency as well as process setting for quality produce. Thus, the present study was planned to determine the applicability of basic dehydration model in predicting the dehydration process leading to obtain a quality dehydrated product with efficient process.
Transcendental dehydration models
Dehydration is a multifaceted unit operation involves moisture exchange through molecular or surface diffusion and capillary, Knudsen or, hydrodynamic flow [12,13]. Effective diffusivity reflects the combined phenomena of all and is defined using Fick’s second law (Eqn. 1)
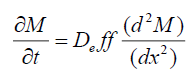 (1)
(1)
Where, M is the moisture concentration (kg moisture/kg dry matter), t is the time (sec), x is the diffusion path (m) and Deff is the effective moisture diffusivity (m2/s). Fick’s second law of diffusion considers heterogeneity into account while predicting effective moisture diffusivity during dehydration process. The solution of differential equation for different regular shaped objects in form of concentration-time-location is available. This law is applicable to predict the uniform distribution of moisture, unidirectional mass transfer, diffusion dependent moisture movement within the solid, surface moisture reaches equilibrium to surrounding air instantly, resistance to the mass transfer at surface is negligible compared to internal resistance, shrinkage of material is negligible and constant diffusion coefficient [14,15].
The drying kinetics of spinach leaves was assessed using basic dehydration models for the time dependent data of dimensionless moisture ratio (MR). The moisture ratio was calculated (Eqn. 2) as:
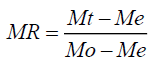 (2)
(2)
Where, Mo, Me and Mt are the initial, equilibrium and moisture at any time t on dry weight basis, respectively. The solution of Fick’s equation for an infinite slab could be obtained as Eqn. 3 or Eqn. 4:
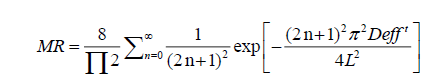 (3)
(3)
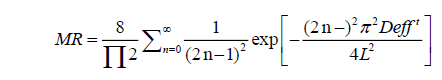 (4)
(4)
Where, MR is dimensionless moisture ratio, Me is the equilibrium moisture content, M0 is the initial moisture content, Mt is moisture content on dry basis (kg moisture per kg of dry matter) at any time t and L is the half thickness, considering the diffusion from both sides of the flat surface. When, 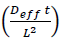 is greater than 0.2, the values of exponential terms decrease rapidly and first three terms (Eqn. 5) provide the value of effective diffusivity to a reasonable accuracy [16].
is greater than 0.2, the values of exponential terms decrease rapidly and first three terms (Eqn. 5) provide the value of effective diffusivity to a reasonable accuracy [16].
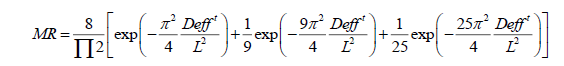 (5)
(5)
For long drying time and for unaccomplished moisture ratios less than 0.6, often first term is considered to be the effective in predicting the dehydration process with good accuracy for the materials of slab geometry. Thus the simplified form of the above series could be represented as (Eqn. 6):
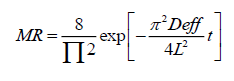 (6)
(6)
The above diffusivity equation based on Ficks theory can be correlated directly with the Henderson and Pabis model (Eqn. 7)
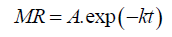 (7)
(7)
Where, A is the shape factor and k is a coefficient known as drying rate constant.
An exponential model, which is analogues to Newton’s law of cooling, often used to predict the dehydration rate constant based on first order kinetics (Eqn. 8) for the drying behavior of biological materials.
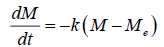 (8)
(8)
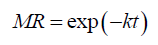 (9)
(9)
The value of A is considered to be 1 in the exponential, Newton or Lewis model (Eqn. 9), which tends to underestimate the dehydration phenomenon during early stage of dehydration and overestimate during the later stage of dehydration. To overcome with these shortcomings the dimensionless exponent (n) is applied to the time term as empirical modification in the exponential or Lewis model forms Page model (Eqn. 10) for the better fit to the dehydration curve.
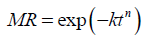 (10)
(10)
The equilibrium moisture content (Me) is comparatively extremely small as compared to the initial moisture content (M0), simplifying MR as M/M0 introduces a maximum of 15% estimated error. These simple semi empirical transcendental models are generally applied to express the relationships between the dehydration constant and the characteristic dimension of the dehydrating sample and applied dehydration temperature in describing the thin layer dehydration behavior.
The overall drying rate (DR) was estimated using the Eqn. 11
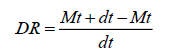 (11)
(11)
where, Mt is moisture content at any time, t, Mo is initial moisture content, Me is equilibrium moisture content, Mt+dt moisture content at t+dt (kg moisture/kg dry matter) and t is the drying time (min).
Materials and Methods
Fresh spinach (Spinacia oleracea) leaves (variety Palak RNG - All Green Akshit) were harvested manually during early morning from the farm nearby Sunam (Punjab) and taken to the laboratory within 45 minutes of harvesting [17]. The fresh and undamaged leaves were sorted and thoroughly washed in running tap water twice to remove the dirt and surface impurities if any. The sorted and prepared spinach leaves were divided in two lots to assess the effect of blanching as pretreatment on dehydration kinetics. The average initial moisture content of leaves was 91.81 ± 1.04% with the surface area to volume ratio as 37.80 × 103 m-1 and leaf thickness as 0.03 × 10-2 m.
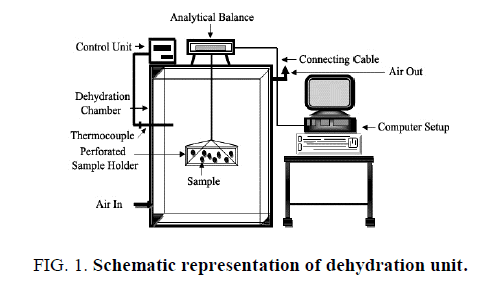
Two minutes blanching in a developed precision steam blancher was provided to prepared leaves for getting the effective and reproducible blanched leaves [18]. The drying kinetics of treated and untreated leaves were deliberated with a modified convective hot air dryer at isothermal drying temperatures of 50 to 90°C with an uniform 10°C interval with having an average temperature fluctuation of ± 1°C (Figure. 1). Approximately, 100g samples were uniformly spread on a square flat perforated non corrosive metal basket (0.30 × 0.30 m2) in a single layer having 95% opening with the sharp edge type contact to make the least contact with the bottom surface of the leaves and place inside the drier after stabilizing the desired drying conditions (Figure. 1). The dehydration process was considered to be convective type for thin infinite slab spinach and heat and mass transfer was considered to be from both the sides of the leaves. The dehydrated leaves so obtained after three hours of drying was cooled and kept in an air tight opaque glass jar and stored at 4 ± 2°C for further experimental use. Drying tests were replicated three times to verify the process.
Experimental setup
The used modified drying system contained number of units and accessories attached to it for effective drying operation e.g. inbuilt thermostat control unit with digital temperature display for effective maintenance of dehydration temperature, additionally attached thermocouple to sense the temperature online, weighing assembly connected with computer to get the online data to the accuracy of third decimal place (Figure. 1). In order to suspend the sample freely in the hot air stream to record its moisture loss continuously, a wire and hook type arrangement was found effective. The weighing balance assembly was attached to the computer interfaced with the developed software program to mark the weight of the sample uninterrupted at every second during entire isothermal dehydration. The dehydration process was carried out during entire dehydration duration without any intervention. The dehydration process was further continued in order to get the equilibrium moisture content.
Statistical analysis
The moisture ratio data was then fitted to the selected basic dehydration models. The parameters in each model were estimated by using Levenberg–Marquardt procedure of non-linear least square regression analysis. Along with the values of the model parameters, the corresponding statistical information is also presented along with the evaluated quality of estimation. These parameters can be calculated as follows:
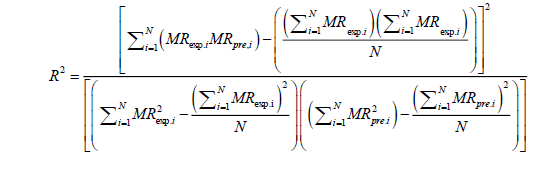 (12)
(12)
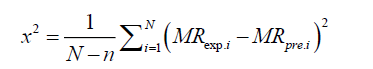 (13)
(13)
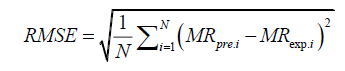 (14)
(14)
where, MRexp,i is the ith experimentally observed moisture ratio, MRpre,i the ith predicted moisture ratio, N the number of observations, and n is the number of constants in the model [19]. Adequacy of fitted model was assessed in terms of coefficient of multiple determination (R2) chi-square (χ2) and root mean square error (RMSE) to ascertain the quality fit with a condition of higher R2 value and lower χ2 and RMSE values [20-25].
Results and Discussion
Drying characteristics
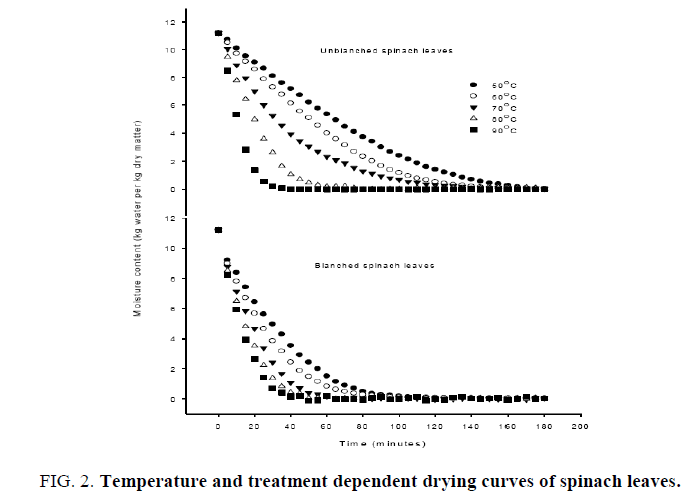
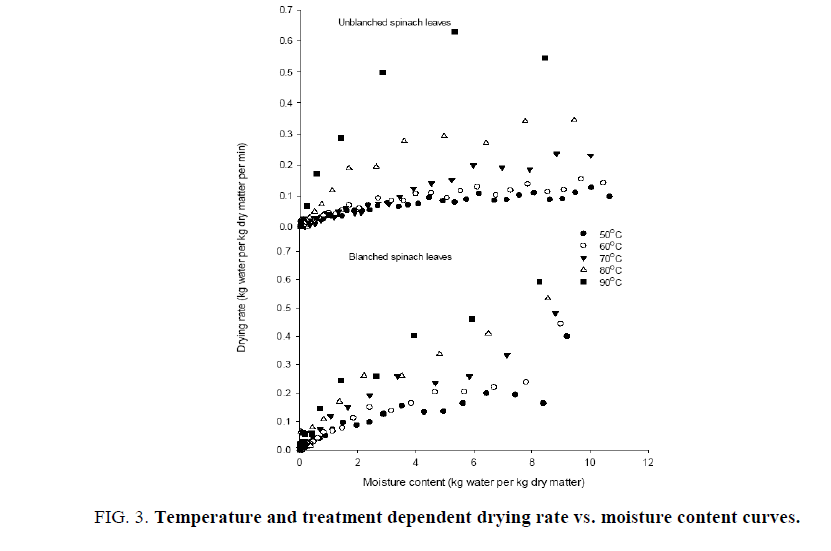
The drying curves presented in Figure. 2 show the effect of isothermal dehydration temperature from 50°C to 90°C with an interval of 10°C on change in the moisture content with respect to time of three hours duration (Figure. 2). The obtained characteristic drying curves for spinach leaves are similar to the dehydration of most fruits and vegetables, which reflect the change in the moisture content is temperature dependent. The initial moisture content of either the raw or unbalanced spinach reduced exponentially in the similar trend but the reduction in moisture of blanched samples was found to be at faster rate as compared to untreated spinach. The heat treatment during blanching affects the integrity of soft plant tissues and thus reduces the barrier of moisture movement, thereby accelerating the moisture loss. The found trend is in agreement with the reported work on other vegetable [26]. With the increase in the drying temperature the drying time has been found to be reduced considerably. The drying time for the unblanched spinach leaves were 175, 160, 150, 70 and 45 min at 50°C, 60°C, 70°C, 80°C and 90°C, respectively. However, the drying time for the blanched spinach leaves were 120, 100, 80, 65 and 40 minutes at 50°C, 60°C, 70°C, 80°C and 90°C, respectively. Figures. 3 and 4 reflects that 60 min exposure to dehydrating leaves are sufficient to get the benefits of higher dehydration rate of blanched leaves as the difference in the moisture content leveled off thereafter. Considering this, the drying time shows a drastic reduction (60%) at higher temperature (80°C) due to increased driving force created due to generated difference in partial vapour pressure between drying leaves and surroundings [27]. This has resulted in an increased moisture transfer rate at higher temperature with the quality dehydrated leaves keeping the dehydration temperature up to 80°C [17,28]. Such an influence of drying air temperature on drying rate was considered as initial dehydration duration for one hour to harness the benefits of higher drying rate and the dehydrating product temperature to be near the wet bulb temperature to get the quality dehydrated produce. Similarity in the reduction of drying time at higher dehydration temperature and less drying time for the blanched samples were observed elsewhere for other vegetables [27,29].
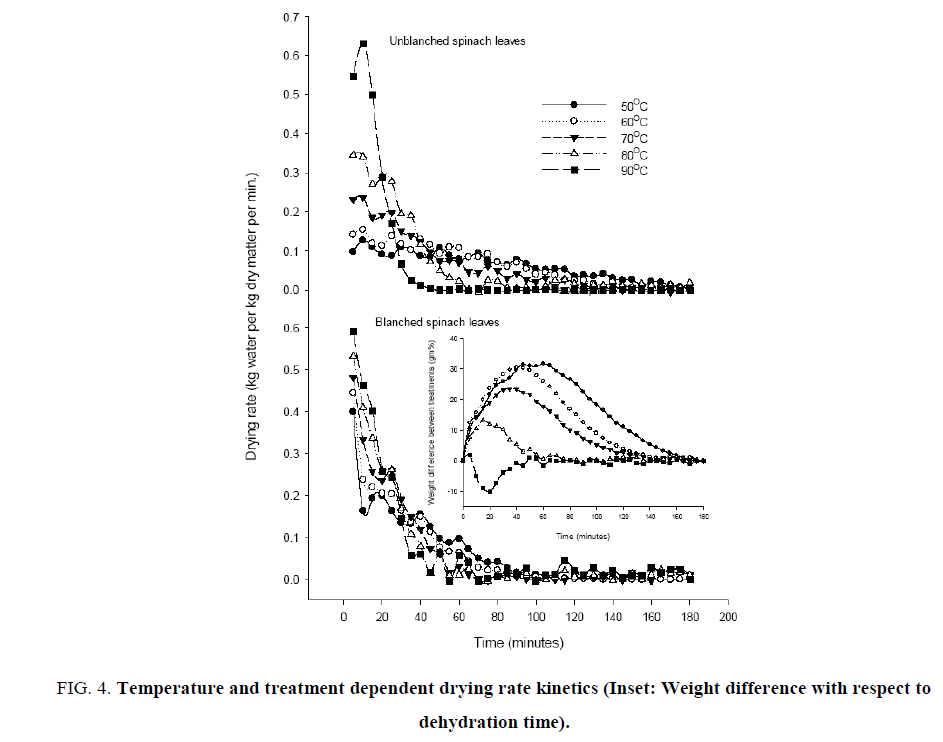
Figure 4: Temperature and treatment dependent drying rate kinetics (Inset: Weight difference with respect to dehydration time).
Drying rate
Isothermal temperature dependent drying rate as function of moisture content for untreated and blanched spinach leaves are shown in Figure. 3. At the initial stage of drying process, drying rate was very high but it became extremely low as the moisture content approached equilibrium (Figure. 3) or drying led to finishing stage (Figure. 4). It is evident that increase in the drying rate during initial adjustment phase leads to the constant drying rate for variable period depending on the exposed dehydration temperature (Figure. 4). Drying of leaves was then followed the falling rate period at all the dehydration temperatures, which reflects the mechanism of diffusion dominates the moisture transfer. Similar results were obtained for green bean [30], okra [31] and red chilli [32]. It is obvious from Figure. 3 and Figure. 4 that increasing the drying temperature caused increase in the drying rate and thereby the decreased drying time. The effect of drying air temperature was most dramatic in decreasing the moisture rapidly with increased temperature. The drying temperature of 60°C during later stage in the double stage dehydration thus be effective as finishing temperature for unblanched spinach samples. Several researchers reported considerable increase in drying rates when higher temperatures were used for drying various vegetables, such as carrot [33-36], eggplant [26] and pumpkin slices [37].
Modeling of drying curve
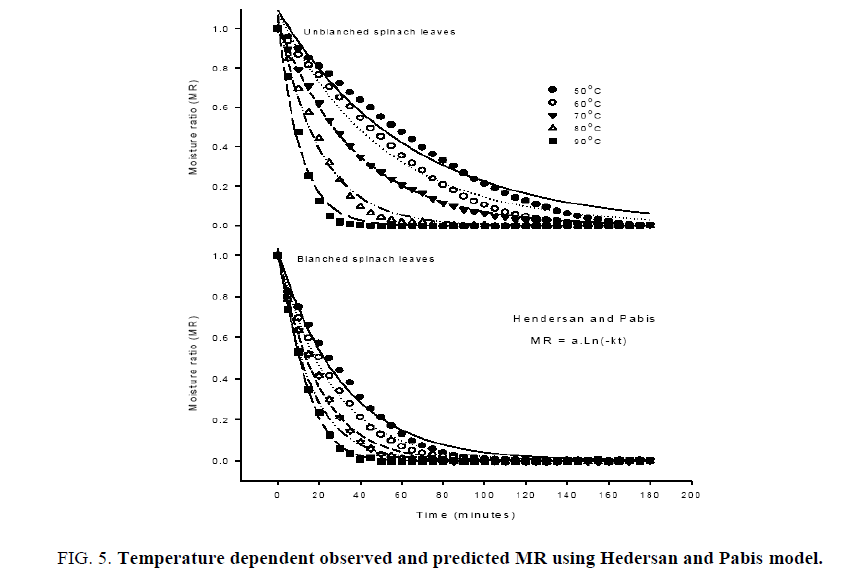
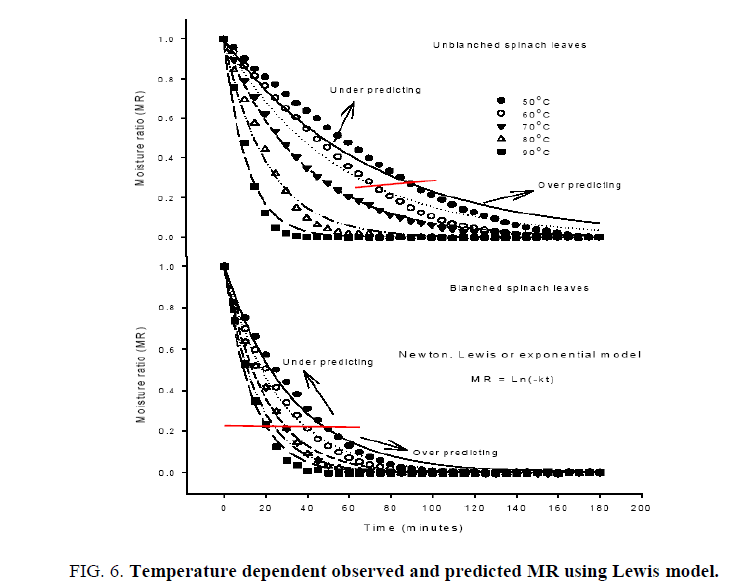
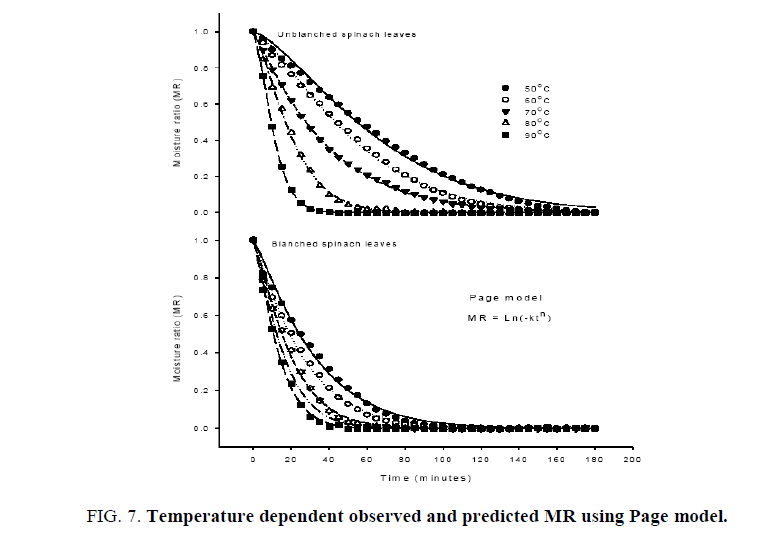
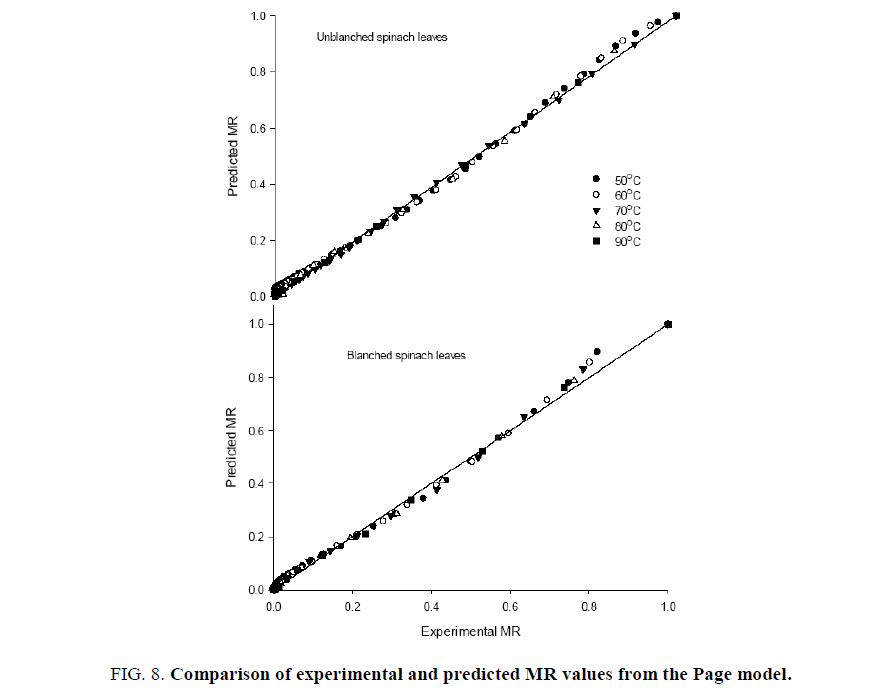
The average moisture content was converted to dimensional moisture ratio for fitting of commonly used semi empirical transcendental models to represent the dehydration behavior of biomaterials. The initial moisture content (M0) is assumed to be as the critical moisture content as per the fitting requirement of models. The dehydration model parameters along with the statistical analyses undertaken on Henderson and Pabis (Eqn. 7), exponential, Lewis or Newton (Eqn. 9) and Page (Eqn. 10) models are shown in Tables 1 and 2. The applicability of fitted models was assessed based on higher R2 values, which was found at least 0.975, 0.965 and 0.9995 for the Hendersan and Pabis, Lewis and Page models, respectively (Table 2). The lower values of R2 for Hendersan and Pabis model and Lewis model with the underestimating the dehydration process during the initial phase of dehydration and over predicting in later stage especially at lower dehydration temperatures (Figures. 5 and 6) restricts their effectiveness as compared to Page model (Figure. 7). The applicability of Page model for the effectiveness was further verified by plotting the experimented data with calculated data (Figure. 8) and reflects the reproducibility. The least values of chi-square (χ2) and root mean square error (RMSE) further confirm the possibility of model in predicting the dehydration process effectively [37,38].
| Type of sample | Temperature (°C) |
Model parameters | ||
|---|---|---|---|---|
| Lewis model | Henderson and Pabis model | Page model | ||
| Unblanched | 50 | k=0.0146 | a=1.0948, k=0.0159 | k=0.0027, n=1.3890 |
| 60 | k=0.0187 | a=1.0909, k=0.0203 | k=0.0041, n=1.3642 | |
| 70 | k=0.0262 | a=1.0312, k=0.0270 | k=0.0184, n=1.0912 | |
| 80 | k=0.0475 | a=1.0681, k=0.0503 | k=0.0156, n=1.3415 | |
| 90 | k=0.0885 | a=1.0586, k=0.0927 | k=0.0250, n=1.4828 | |
| Blanched | 50 | k=0.0314 | a=1.0252, k=0.0321 | k=0.0170, n=1.1646 |
| 60 | k=0.0386 | a=1.0160, k=0.0392 | k=0.0257, n=1.1159 | |
| 70 | k=0.0512 | a=1.0331, k=0.0527 | k=0.0266, n=1.2023 | |
| 80 | k=0.0627 | a=1.0337, k=0.0646 | k=0.0341, n=1.2022 | |
| 90 | k=0.0746 | a=1.0394, k=0.0771 | k=0.0353, n=1.2636 | |
Table 1. Dehydration model parameters.
| Temperature (°C) |
Type of sample |
Model name | Statistical parameters | ||
|---|---|---|---|---|---|
| R2 | χ2 | RMSE | |||
| 50 | Unblanch | Henderson and Pabis | 0.9751 | 0.0025 | 0.0497 |
| Lewis | 0.9653 | 0.0034 | 0.0587 | ||
| Page | 0.9957 | 0.0004 | 0.0206 | ||
| Blanch | Henderson and Pabis | 0.9902 | 0.0007 | 0.0271 | |
| Lewis | 0.9897 | 0.0008 | 0.0278 | ||
| Page | 0.9949 | 0.0004 | 0.0196 | ||
| 60 | Unblanch | Henderson and Pabis | 0.9801 | 0.0020 | 0.0443 |
| Lewis | 0.9725 | 0.0027 | 0.0521 | ||
| Page | 0.9969 | 0.0003 | 0.0168 | ||
| Blanch | Henderson and Pabis | 0.9947 | 0.0004 | 0.0189 | |
| Lewis | 0.9945 | 0.0004 | 0.0193 | ||
| Page | 0.9970 | 0.0002 | 0.0140 | ||
| 70 | Unblanch | Henderson and Pabis | 0.9983 | 0.0001 | 0.0118 |
| Lewis | 0.9974 | 0.0002 | 0.0142 | ||
| Page | 0.9995 | 0.0000 | 0.0066 | ||
| Blanch | Henderson and Pabis | 0.9921 | 0.0005 | 0.0215 | |
| Lewis | 0.9913 | 0.0005 | 0.0226 | ||
| Page | 0.9969 | 0.0002 | 0.0134 | ||
| 80 | Unblanch | Henderson and Pabis | 0.9889 | 0.0008 | 0.0278 |
| Lewis | 0.9855 | 0.0010 | 0.0315 | ||
| Page | 0.9989 | 0.0001 | 0.0091 | ||
| Blanch | Henderson and Pabis | 0.9944 | 0.0003 | 0.0176 | |
| Lewis | 0.9935 | 0.0004 | 0.0190 | ||
| Page | 0.9987 | 0.0001 | 0.0087 | ||
| 90 | Unblanch | Henderson and Pabis | 0.9856 | 0.0007 | 0.0261 |
| Lewis | 0.9830 | 0.0008 | 0.0283 | ||
| Page | 1.0000 | 0.0000 | 0.0023 | ||
| Blanch | Henderson and Pabis | 0.9927 | 0.0001 | 0.0080 | |
| Lewis | 0.9915 | 0.0004 | 0.0199 | ||
| Page | 0.9990 | 0.0001 | 0.0080 | ||
Table 2. Statistical parameters of fitted models.
Drying rate constant
The value of drying rate constant (k) has been found to increase with the increase in drying temperature for all the fitted models (TABLE 1). Increase in the value of k at higher temperature may be attributed to temperature dependent faster removal of moisture, which reflects the dependence of this parameter on the temperature used for dehydration. The insignificant change in the value of Hendersan and Pabis model empirical constant (a) of and dimensionless exponent (n) of Page model reflects least dependency on temperature alone (TABLE 1).
Effective moisture diffusivity and activation energy
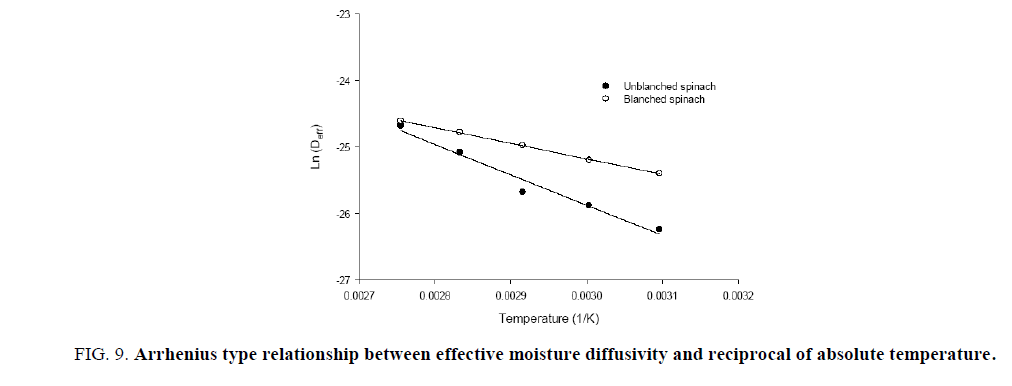
The drying process of spinach leaves was found to have taken place in falling rate period with short initial adjustment phase. The average effective moisture diffusivity, (Deff) was calculated by taking the arithmetic mean of the effective moisture diffusivities that were estimated at various levels of moisture contents during the course of drying. The average moisture diffusivity (Deff) increased with increase in temperature and the increase is more in case of blanched sample (Figure. 9). This higher moisture evaporation rate influences higher rate of moisture diffusion from the internal regions of the leaves to the surface which increases the diffusion coefficients. Blanching although softens leaf tissues to remove air from internal cellular mass spaces and permit better diffusion [39] also due to loss of tissues cell integrity accelerates shrinkage and form lumps and resist diffusion to proceed effectively. Deff found to vary in the range 1.380 × 10-11 to 4.720 ×10-10 m2/s and 2.204 × 10-11 to 4.303 × 10-10 m2/s for the untreated and blanched leaf samples, respectively. Similar variations were observed elsewhere during drying of amaranth leaves [40], red pepper slices [41], micro wave treated mint leaves [42], vacuum drying of pumpkin [43].
Figure 9: Arrhenius type relationship between effective moisture diffusivity and reciprocal of absolute temperature.
The temperature dependence of effective diffusivity could be expressed using the Arrhenius type equation [44].
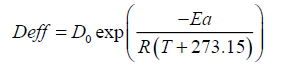 (15)
(15)
Where D0 is the Arrhenius factor (m2/s), Ea is the activation energy for the moisture diffusion (kJ/mol), R is the universal gas constant (kJ/ mol), and T is drying air temperature (°C).
The activation energy (Ea) was calculated from the slope of the plot ln (Deff) versus the reciprocal of temperature, 1/(T+273.15) from FIG. 9.
The lower activation energy of blanched leaves due to mentioned reasons elsewhere is an indication that less energy is required for evaporation of moisture during dehydration as compared to untreated leaves. The activation energies were found to be 39.74 kJ/mol and 19.23 kJ/mol and moisture diffusivity was found 5.107 × 10-6 m2/s and 1.204 × 10-8 m2/s for untreated and blanched spinach leaves, respectively. The activation energy value is comparable to that of 34.35 kJ/mol for spinach leaves, 35.05 kJ/mol for dill leaves, 62.96 kJ/mol for mint leaves, 43.92 kJ/mol, for parsley leaves and pepper 39.70kJ/mol [ 15,38]. The values of activation energy are generally within the range of 12 to 110 kJ/mol for food materials [45].
Conclusion
Effect of blanching spinach leaves on dehydration kinetics was studied between 50°C and 90°C. Increase in drying rate was observed with increase in dehydration temperature led to reduce drying time. To an extent of 60% shortening of drying time has been found to yield the dehydrated leaves when dried at 80°C as compared to 50°C. The double stage dehydration keeping 80°C for 1 hour as initial temperature and finishing with 60°C may not only save the energy and time but also help in production of quality product with the unblanched spinach. The Fitting of basic dehydration model confirmed the applicability of Page model in predicting the dehydration kinetics effectively. Effective moisture diffusivity was found to be temperature dependent and varied in the range 1.380 × 10-11 to 4.720 × 10-10 m2/s and 2.204 ×10-11 to 4.303 ×10-10 m2/s over considered dehydration range of temperature for untreated and blanched spinach leaves, respectively. The temperature dependence effective moisture diffusivity in form of activation energy was found to be 39.74 kJ/mol for untreated and 19.23 kJ/mol for blanched spinach.
Acknowledgement
First author is thankful to Mr. Lokesh Kumar of Starcom Information Technology Limited, Bangalore for providing the key to use Sigma Plot software to accomplish the project.
References
- Salunkhe DK, Kadam SS. Handbook of vegetable science and technology. Madison avenue publishers, New York, 2005.
- Nisha P, Singhal R, Pandit AA. Study on the degradation kinetics of visual green colour in spinach (Spinacea oleracea L.) and the effect of salt therein. J Food Eng. 2004;64:135-42.
- Chakraverty A, Singh RP. Postharvest technology and food process engineering. CRC Press, Boca Raton, FL, 2014.
- Singh Y, Yadav P, Kumar D, et al. Drying: An approach towards food preservation. In: Emerging science and technology for food, agriculture and environment. In: Kumar S, et al. (Ed). Agrobios (International) Publishers, Jodhpur, India, 2013.
- Prasad K, Nath N, Nanjundaswamy AM. Dehydration behaviour of plain and fortified mango pulps in the preparation of bars. J Trop Agric and Fd Sci. 2002;30:83-8.
- Prasad K. Dehydration behaviour of plain and fortified banana pulps in the preparation of bars. J Dairy Foods Home Sci. 2010;29:37-41.
- Grabowski S, Marcottre M, Ramaswamy HS. Drying of fruits, vegetables, and spices. Marcel Dekker, New York, 2003.
- Souraki B, Andre A, Mowlac D. Mathematical modeling of microwave-assisted inert medium fluidized bed drying of cylindrical carrot samples. Chem Eng Prog. 2009;48:296-305.
- Von Elbe JH, Schwartz SJ. Food chemistry. Marcel Dekker Inc., New York, 1996.
- Ankita, Prasad K. Characterization of dehydrated functional fractional radish leaf powder. Der Pharmacia Lettre. 2015;71:269-79.
- Cai T, Chen F, Qi J. Dehydrated oriental mushrooms, leafy vegetables and food preparation herbs and condiments. Marcel Dekker, New York, 2004.
- Mujumdar AS. Handbook of industrial drying. CRC Press, Boca Raton FL, 2015.
- Sharma G, Prasad S. Drying of garlic (Allium sativum) cloves by microwave-hot air combination. J. Food Eng. 2001;50:99-105.
- Crank J. The mathematics of diffusion. Oxford University Press, Glasgow, 1975.
- Domyaz I. Thin layer drying behavior of mint leaves. J Food Eng. 2006;74: 370-5.
- Das H. Food processing operation analysis. Asian Book Pvt. Ltd., New Delhi, 2005.
- Ankita, Prasad K. Characterization of dehydrated functional fractional spinach powder. Biotechnol Ind J. 2015;11:426-35.
- Prasad K, Singh Y. In 19th International Drying Symposium (IDS 2014) Lyon, France, 2014.
- Ankita, Prasad K. Chemical and physical characterization of dehydrated functional fenugreek leaf powder. Chem Asian J. 2015;27:3697-703.
- Badwaik LS, Prasad K, Seth D. Optimization of ingredient levels for the development of peanut based fiber rich pasta. J. Food Sci Technol. 2014;51:2713-9.
- Prasad K, Vairagar PR. Instant chickpea splits: Optimization using Response Surface Methodology. Lambert Academic Publishing, Germany, 2014.
- Prasad K, Singh Y. Rice based vegetable supplemented functional instant soup mix: Development and optimization. Scholars’ Press, Germany, 2014.
- Sridhar V, Prasad K, Choi S, et al. Optimization of physical and mechanical properties of rubber compounds by response surface methodological approach. J Appl Polym Sci Symp. 2001;82:997-1005.
- Prasad K, Sharma HK. Compositional optimization of whey based mango beverage using response surface methodology. Egyptian J Dairy Sci. 2001;30:75-81.
- Prasad K, Vairagar PR, Bera MB. Temperature dependent hydration kinetics of Cicer arietinum splits. Food Res Int. 2010;43:483-8.
- Ertekin C, Yaldiz O. Drying of eggplant and selection of a suitable thin layer drying model. J Food Eng. 2004;63:349-59.
- Kaleemullah S, Kailappan R. Monolayer moisture, free energy change and fractionation of bound water of red chillies. J Stored Prod Res. 2007;43:104-10.
- Ankita, Prasad K. Studies on spinach powder as affected by dehydration temperature and process of blanching. IJAFST. 2013;4:309-16.
- Giri SK, Prasad S. Drying kinetics and rehydration characteristics of microwave - vacuum and convective hot-air dried mushrooms. J Food Eng. 2007;78:512-21.
- Rosello C, Simal S, Sanjuan N, et al. Nonisotropic mass transfer model for green bean drying. J Agric Food Chem. 1997;45:337-42.
- Gogus F, Maskan M. Water adsorption and drying characteristics of okra (Hibiscus esculentus L.). Drying Technol. 1999;17:883-94.
- Gupta P, Ahmed J, Shivhare US, et al. Drying characteristics of red chilli. Drying Technol. 2002;20:1975-87.
- Prabhanjan DG, Ramaswamy HS, Raghavan GSV. Microwave-assisted convective air drying of thin layer carrots. . J Food Eng. 1995;25:283-93.
- Haq Ru, Kumar P, Prasad K. Hot air convective dehydration characteristics of Daucus carota var. Nantes. Cogent Food Agric. 2015;1:1096184.
- Haq Ru, Kumar P, Prasad K. Influence of Drying Kinetics on Moisture Diffusivity, Carotene Degradation and Nonenzymatic Browning of Pretreated and Untreated Carrot Shreds. J Food Process Preserv 2016;41:12785.
- Haq Ru, Prasad K. Antioxidant activity, phenolic, carotenoid and color changes in packaged fresh carrots stored under refrigeration temperature. Journal of Food Measurement and Characterization. 2017;1-8.
- Doymaz I. The kinetics of forced convective air-drying of pumpkin slices. J Food Eng. 2007;79:243-8.
- Vega A, Fito P, Andre A, et al. Mathematical modeling of hot-air drying kinetics of red bell pepper (var. Lamuyo). J Food Eng. 2007;79:1460-6.
- Ritirut W, Siripatana C. The influence of blanching on mass transfer characteristics during osmotic dehydration of bilimbi fruit. KKU Engineering Journal. 2009;36:151-63.
- Akonor PT, Amankwah EA. Thin layer drying kinetics of solar-dried Amaranthus hybridus and Xanthosoma sagittifolium leaves. J Food Process Technol. 2012;3:42585.
- Akpinar E, Bicer Y, Yildiz C. Thin layer drying of red pepper. J Food Eng. 2003;59:99-104.
- Ozbek B, Dadali G. Thin-layer drying characteristics and modelling of mint leaves undergoing microwave treatment. J Food Eng. 2007;83:541-9.
- Arevalo-Pinedo A, Murr F. Kinetics of vacuum drying of pumpkin (Cucurbita maxima): Modelling with shrinkage. J Food Eng. 2000;76:562-7.
- Akgun NA, Doymaz I. Modeling of olive cake thin layer drying process. J Food Eng. 2005;68:455-61.
- Mwithiga G, Olwal JO. The drying kinetics of kale (Brassica oleracea) in a convective hot air dryer. J Food Eng. 2005;71:373-8.