Original Article
, Volume: 12( 2)Modified Fractional-Order Activated Sludge Model (MFASM) for Aerobic Microbial Growth in Wastewater
- *Correspondence:
- El-Seddik Department of Civil Engineering, Environmental and Sanitary Engineering Division, Institute of Aviation Engineering and Technology (IAET), Giza, Egypt
Tel: +201097931177; +201223623360; E-mail: mostafa.elseddik@iaet.edu.eg
Received Date: September 05, 2017 Accepted Date: September 08, 2017 Published Date: September 13, 2017
Citation: Mostafa M, El-Seddik. Modified Fractional-Order Activated Sludge Model (MFASM) for Aerobic Microbial Growth in Wastewater. Inorg Chem Ind J. 2017;12(2):117
Abstract
This paper presents a modified fractional-order activated sludge model (MFASM) for substrate degradation and nutrient removal. The modified model is based on Activated Sludge Model 1 (ASM1) for bacterial growth incorporated with the hereditary growth of microorganisms in a couple of pH value acclimatizing proton translocation theory for substrate dissociation. A novel modification is accomplished in the ASM to obtain the extra degree of freedom for biomass concentration through fractional order derivatives based on Grünwauld-Letinkov numerical technique. A significant decline in Chemical Oxygen Demand (COD) and NH4-N removal efficiency from 85% to 60% can be obtained as the biomass fractional order fluctuates between 0.9 and 0.1. Also, the specific growth rate of bacteria can be simulated over long time periods to reveal the history of accumulated biomass in activated sludge process. Moreover, the integer order model of ASM can be indicated at fractional order of 1. In this regard, the MFASM is strictly investigated to reveal the influence of both pH value and heterotrophic biomass deterioration on effluent COD. Furthermore, the simulated results are examined for the long term interaction of autotrophs in nitrification process.
Keywords
Biomass growth; COD; Fractional model; Modified ASM1; Nitrification
Introduction
In the past centuries, derivatives and integrals were only considered by the mathematicians as integer order systems known as classical calculus. Although the birth of classical calculus is related Leibniz and Newton, the early stages of fractional calculus can be attributed to Leibniz alone. In 1695, Fractional derivative was firstly recognized in a letter from Leibniz to L’Hospital in an explanation request for non-integer derivatives. Fractional derivatives didn’t come to end by the death of Leibniz in 1716. Factorials generalization was then accomplished by [1] to express the Gamma function for fractional order derivatives. Consecutively, a book was presented by [2] to exhibit a detailed definition for the fractional derivatives. In a couple of years, Lacroix could generalize the integer derivatives into fractional ones with development continued by [3], the year that Niels Abel managed to solve a problem in physics by implementation of integral equation. A basic study of fractional calculus was firstly revealed by [4] after Abel’s physical application for fractional operators. Liouville presented two definitions for fractional calculus. However some restrictions related to ignorance of historical terms could be found. Beyond the historical reason, the use of complementary function was considered to be another deficiency regarding Liouville definition of fractional order. Later on, more modifications were introduced in order to face the previous limitations and reach accurate definitions for fractional order derivative and integral. The complementary function was developed by [5] to exhibit more trusted definition for fractional calculus based on generalized Taylor series. However, the existence of infinity arbitrary constants in the developed complementary function was still a limitation. On the other hand, Grünwald-Letinkov [6,7] showed an accurate definition for fractional order derivatives based on integer derivatives. In 1927, more developments were accomplished for fractional derivative based on Grünwald-Letinkov. In 1974, fractional calculus applications were firstly revealed in a conference in New Haven to show the role of fractional order systems in different fields. Consecutively, fractional calculus has strictly revealed a source of manufacture in control systems, medical improvement, biochemical analyses, biological investigation, and mechanical and physical areas [8-11]. Grünwald-Letinkov formula has been used till today in several numerical methods to show the effect of fractional orders on the design and control of circuits where the historical terms are considered in simpler function.
Several activated sludge models ignored the historical response of biomass in substrate degradation [12-14]. The former activated sludge model only considers the specific growth rate of bacteria on short term periods [15,16]. Even the impact of biomass fluctuation on treatment process can’t be recognized in the previous activated sludge models. The aim of this work is to extract the extra degree of freedom of biomass concentration in the activated sludge systems. Accordingly, modified fractional-order activated sludge model (MFASM) is established to explore the microorganism’s behavior on periodically long terms and to investigate the influence of pH value on substrate dissociation. The modified model is based on the fractional order derivative of ASM1 and proton translocation theory [17,18]. Grünwald-Letinkov numerical technique [19] is applied in Matlab software to simulate the mass balance equations of MFASM. A novel alternation is accomplished by long term biomass-substrate interaction coupled with hydrolysis of unionized organic substrates. A significant decline in the effluent COD is associated with the change of biomass concentration in the activated sludge process. Moreover, both COD removal and nitrification process can be simulated at various pH values and different fractional orders. In addition, the MFASM is examined at various influent COD where simulation results illustrate the influence of pH value on specific growth rate of heterotrophic aerobic and anoxic bacteria. Furthermore, an impressive reduction in NH4-N can be achieved by the extra degree of freedom of autotrophic nitrifiers.
Materials and Methods
Description of the MFASM model
The ASM1 is modified to incorporate the hereditary effect of biomass with proton translocation theory. The modified model considers the unionized substrate molecules as the sole available substrate for heterotrophic and autotrophic microorganisms. The logic behind this hypothesis is that proton the gradient between the inside and outside of the cell membrane should be kept constant to maintain a constant pH during substrate degradation. According to the proton translocation theory, proton pumps are activated during the respiration cycle to generate energy needs for the viable cell. Therefore only unionized weak acids are free to be transported through the membrane and utilized as a substrate by the aerobic microorganisms. Figure 1(a) shows the hydrolysis process of unionized organic substrates in the MFASM. The complex substrate organics (CS ) dissociate into less molecular compounds under the effect of pH value. The unionized substrate molecules (CHS ) are directly utilized by bacteria in the growth process, whereas the dissolved oxygen (DO) is consumed by bacteria in the feast period to increase the biomass concentration (CX ) under the bacterial kinetics as shown in Figure 1(b). In this regard, substrate biodegradation can be attributed to short term specific growth rate of bacteria (µS ) whereas the long term bacterial growth rate (µ1 ) is proposed for biomass conversion to its impacts (CXβ ). Several values of the fractional order (β) varying between are considered for biomass rate of change while a predominant order close to is used for substrate rate of change. The kinetic parameters of ASM1 are shown in Table 1 at 600 mg/l as COD and 100 mg/l as NH4-N [12,20,21]. Grünwald-Letinkov numerical technique is applied to simulate the modified model based on [19]. The biomass and substrate mass balance equations for the modified model are:
Figure 1: Schematic block diagram for proton translocation in activated sludge and (b) Schematic block diagram for bacterial kinetics in the MFASM.
| Symbol | IAWQ model parameters | Value | Reference |
|---|---|---|---|
| CSIH | Initial soluble COD concentration (g/m3) | 600 | Current study |
| CSIN | Initial NH4-N concentration (g/m3) | 100 | |
| CXiH | Initial heterotrophic biomass concentration (kg/m3) | 60 | |
| CXiN | Initial autotrophic biomass concentration (kg/m3) | 3 | |
| CNO3 | Nitrate concentration (g/m3) | 40 | |
| CO3 | Dissolved oxygen concentration (g/m3) | 5 | |
| HRT | Hydraulic retention time (hr) | 8 | |
| KO2H | Oxygen half saturation coefficient for heterotrophs (gO2m-3) | 0.8 | [12,15] |
| K02A | Oxygen half saturation coefficient for Autotrophs (gO2m-3) | 2 | [12] |
| Kno | Nitrate half saturation coefficient (gO3m-3) | 1.7 | [15] |
| KS | Monod half-saturation coefficient for heterotrophs (gCOD m-3) | 61 | [22] |
| KA | Dissociation constant | 0.0001 | [18] |
| Kno | Monod half-saturation constant for nitrifiers (gNH3 m-3) | 1.49 | [20,22] |
| KdH | Decay rate for heterotrophs (d-1) | 0.067 | [12] |
| KdA | Decay rate for autotrophic bacteria (d-1) | 0.035 | [22] |
| µH max | Max. aerobic heterotrophic rate of growth (d-1) | 6.4 | [15,23] |
| µA max | Max. autotrophic rate of growth (d-1) | 0.62 | [21,22] |
| ?gr | Anoxic growth factor for heterotrophs (d-1) | 0.18 | [15] |
| YH | Yield coefficient for heterotrophs | 0.45 | [12] |
| YA | Yield coefficient for autotrophs (nitrifiers) | 0.07 | [20] |
Table 1. Kinetic and stoichiometric constants of ASM1 for substrate biodegradation and nitrification and denitrification process at 20°C.
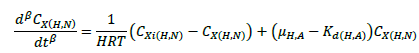 (1)
(1)
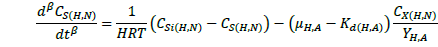 (2)
(2)
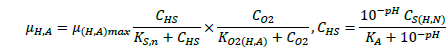 (3)
(3)
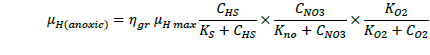 (4)
(4)
Results and Discussion
Influence of pH on microbial growth rate
The influence of proton translocation on both COD removal and nitrification process is discussed for the modified model at integer order of β = 1.0 Figure 2 shows the role of pH value in the dissociation of unionized organic substrate and microbial growth rate. An increase in the effluent COD from 0.05 to 0.3 kg/m3 is achieved by increasing pH value from 6 to 8 for influent COD of 0.6 kg/m3 and heterotrophic biomass concentration (CHX) of 60 kg/m3. The simulated results demonstrate that higher effluent COD is attributed to the pH value [18]. Also, a decline in the COD removal efficiency is recognized as a result of a minor decrement in the specific growth rate of heterotrophic anoxic bacteria from 0.0004 hr-1 to about 0.0001 hr-1 pH varying from 6 to 8 Moreover, the simulated results show that the effluent NH4-N increases from 0.01 to 0.05 kg/m3 as pH fluctuates from for influent NH4-N of 0.1 kg/m3 and nitrifier concentration (CXN) of 3 kg/m3. Although the maximum specific growth rate of nitrifying bacteria increases at pH of 8 [21], a decline in effluent NH4-N occurs at the same pH. The reason behind that is the significant influence of pH value on the dissociation of unionized organic substrate which affects the microbial growth rate.
Figure 2: The influence of pH value on COD removal by heterotrophic aerobic and anoxic bacteria and NH4-N removal at integer order model.
Simulation results of the modified model
The influence of biomass deterioration on the treatment process can be revealed by varying the fractional order in the MFASM at pH of 7 as shown in Figure 3. The simulated results strictly demonstrate that a decline in (CXH) from 60 to 10 kg/m3 is accomplished by reducing β from 0.9 to 0.1. Accordingly, both COD and NH4-N removal efficiency decrease from 85% to 60% over long term period where β reaches low values. Figure 3 also indicates that the extra degree of freedom of biomass concentration can be the predominant effect on the substrate degradation [18]. The biomass concentration decreases as a result of the increase in specific growth rate of bacteria and thus the substrate concentration increases. This may owe to that the decline in biomass concentration is much higher than the increase in microbial growth rate. In this regard, the MFASM can generalize the impact of activated sludge microorganisms on the treatment process. The simulated results of MFASM can be strictly displayed for heterotrophs and autotrophs as shown in Figure 4(a)-4(b). Several fractional orders can be admitted to show the gradual decline in (CXH) till about 10 kg/m3 as indicated in Figure 4(a) where the typical values of MLSS and MLVSS [22,23] can be approached at COD of 600 mg/l. However, the increment in the influent COD may be a limitation for MLSS and MLVSS. Moreover, a significant decline in COD till about 600 mg/l is associated with aerobic heterotrophic growth on influent COD of 600 mg/l at 8 hr operation as obtained in Figure 4(b).
Figure 3: The simulation results of heterotrophic biomass concentration, COD removal by heterotrophic aerobic bacteria and nitrification process for MFASM.
Consecutively, Figure 4(c) shows that CXN deteriorates from 3 kg/m3 to about 0.5 kg/m3 at low fractional orders that significantly affect the nitrification process. Accordingly, the effluent NH4-N can be obtained in the range of 20 to 50 mg/l in MFASM at 8 hr operation for influent NH4-N of 100 mg/l as revealed in Figure 4(d). It is evident from results that the impressive decrement in ammonia nitrogen is relevant to CXN in MFASM. Also, the performance of activated sludge wastewater treatment plants can be related to the flexibility provided by modified model.
Conclusion
The microbial growth of heterotrophs and autotrophs could be strictly investigated on periodically long terms through MFASM that leads to a significant decline in both COD and NH4-N removal from 80% to 60% by varying β from0.9 to 0.1. Extra degree of freedom could be obtained for biomass concentration where heterotrophs deteriorated from 60 kg/m3 to 10 kg/m3 at influent COD of 600 mg/l. Also, a decrement in nitrifiers from 3 kg/m3 to 0.5 kg/m3 could be reached at influent NH4-N of 100 mg/l. On the other hand, higher effluent COD could be attributed to low microbial growth of anoxic heterotrophs at NO3 of 40 mg/l. Moreover, a significant influence of pH value on dissociation of unionized substrate could be indicated by varying pH between 6 and 8. The substrate removal efficiency could be enhanced at pH fluctuating between 6 and 7 for influent COD of 600 mg/l. The nitrification process could be also promoted at pH= 6 - 7 for influent NH4-N of 100 mg/l although maximum specific growth rate of nitrifiers occurs at pH of 8. The reason behind that may owe to the role of pH value in the proton translocation theory that associate microbial growth rate with the hydrolysis and dissociation of unionized organic substrates influencing substrate degradation.
Acknowledgements
The author acknowledges the International Association on Water Quality (IAWQ) for the technical perspectives of establishing the Activated Sludge Model No. 1 (ASM1) provided with available values for kinetic and stoichiometric parameters.
References
- Euler L. De progressionibus transcendendibus seu quarum termini generales algebraicae dari nequent. Comm Acad Sci Petropolitanae. 1738;5:36-57.
- Laplace PS. Théorie analytique des probabilités, Imprimeur-Libraire pour les Mathématiques, Paris, 1820, pp:85-156.
- Fourier JB. J Théorie analytique de la chaleur. Didot, Paris, 1822. p:561-62.
- Liouville J. Mémoire sur le calcul des différentielles à indices quelconques. J l'Ecole Roy Polytéchn. 1832; 13:71-162.
- Riemann B. Versuch einer allgemeinen Auffassung der Integration und Differentiation, in Gesammelte Mathematische Werke und Wissenschaftlicher. Leibzig; Teubner, 1876.
- Grünwald AK. Ueber “begrenzte” Derivationen und deren Anwendung. Z Angew Math and Phys. 1867; 12:441-80.
- Letnikov AV. Theory of differentiation with an arbitrary index (Russian). Moscow Matem Sbornik. 1868;3:1-66.
- Ortigueira M, Machado J. Special issue on fractional calculus applications in signals and systems. Signal Process.2006;86.
- Jesus I, Machado J, Cunha J. Fractional electrical impedances in botanical elements. J Vib Control. 2008; 14:1389-402.
- Radwan AG, Elwakil AS, Soliman AM. Fractional-order sinusoidal oscillators: Design procedure and practical examples. IEEE Trans Circuits Syst I. 2008;55:2051-63.
- Ionescu C, De Keyser R. Relations between fractional-order model parameters and lung pathology in chronic obstructive pulmonary disease. IEEE Trans Biomed Eng. 2009;56:978-87.
- Henze, M, Gujer W, Mino T, et al. Activated sludge models ASM1, ASM2, ASM2-d and ASM3. IWA publishing, Scientific and Technical Report series, London, UK, 2000.
- Boltz JP, Morgenroth E, Brockmann D, et al. Systematic evaluation of biofilm models for engineering practice: Components and critical assumptions. Water Sci Technol. 2011;64:930-44.
- Mostafa NG, Galal MM, Radwan AG, et al. Comparison and database development of four recent ASM3 model extensions. ASCE J Environ Eng. 2016.
- Sriwiriyarat T. Mathematical modeling and evaluation of IFAS wastewater treatment processes for biological nitrogen and phosphorus removal (Doctoral dissertation). Civil and Environmental Engineering Department, Virginia Polytechnic Institute and State University. 2002.
- Baalbaki Z, Torfs E, Maere T, et al. Dynamic modelling of solids in a full-scale activated sludge plant preceded by CEPT as a preliminary step for micropollutant removal modelling. Bioprocess Biosys Eng. 2017; 40:499-510.
- Ruiz G, Jeison D, Chamy R. Nitrification with high nitrite accumulation for the treatment of wastewater with high ammonia concentration. Water Res. 2003;37:1371-77.
- El-Seddik MM, Galal MM, Radwan AG, et al. Modified kinetic-hydraulic UASB reactor model for treatment of wastewater containing biodegradable organic substrates. Water Sci Technol. 2016;73,1560-71.
- Petras I. Fractional-order nonlinear systems: Modeling, analysis and simulation. Springer Science & Business Media. 2011.
- Van Haandel AC. Nitrification and denitrification kinetics in the activated sludge process. (Doctoral dissertation), University of Cape Town. 1981.
- Blackburne R, Vadivelu VM, Yuan Z et al. Determination of growth rate and yield of nitrifying bacteria by measuring carbon dioxide uptake rate. Water Environ Res. 2007;79:2437-45.
- Mardani SH, Mirbagheri A, Amin MM et al. Determination of biokinetic coefficients for activated sludge processes on municipal wastewater. Iran J Environ Health Sci Eng. 2011;8:25-34.
- Gujer W, Henze M, Mino T, et al. The activated sludge model No. 2: Biological phosphorus removal. Water Sci Technol. 1995;31:1-11.