Short commentary
, Volume: 14( 3)Influence of Acoustic Vibrations on the Kinetics and Mechanism of FirstOrder Chemical Reactions in Nano-structured Liquid Phase
- *Correspondence:
- Kulagina TP, Institute of Problems of Chemical Physics RAS, Semenov prospect, Chernogolovka, Moscow region, 142432, Russia, Tel: +74965221879; E-Mail: tan@icp.ac.ru
Received: November 08, 2018; Accepted: November 22, 2018; Published: December 02, 2018
Citation: Kulagina TP, Smirnov LP, Chegodaev NA. Influence of Acoustic Vibrations on the Kinetics and Mechanism of First-Order Chemical Reactions in Nano-structured Liquid Phase. Org Chem Ind J. 2018;15(1):132
Abstract
Introduction
As is known [1-3], acoustic vibrations (10-100 Hz) may affect the kinetics of chemical reactions in some specific conditions [1-3]. In this work, we modeled the impact of acoustic vibrations on the rate of first or second-order liquid-phase reactions with due regard for the formation of associates.
The scheme of the first-order reaction yielding product B from monomers A1 and dimers A2 can be written [1,4] as:
Mathematical Model
A1 → B, k1 (1)
A2 → B + A1, k2 (2)
2A1↔ A2, k (3)
Where K is the equilibrium constant.
Accordingly, the expression for reaction rate w acquires the form [1]:
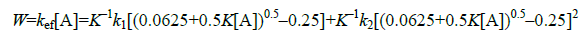 (4)
(4)
The strain/compression waves induced in the solution by acoustic waves of frequency ν affect the equilibrium constant Kν(t) for dissociation of the associates. According to Chegodaev NA et al., and Kulagina TP et al. [4,5], the latter can be written in the form:
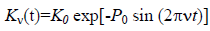 , (5)
, (5)
Where K0 is the equilibrium constant without the external action, P0 is the amplitude of applied field.
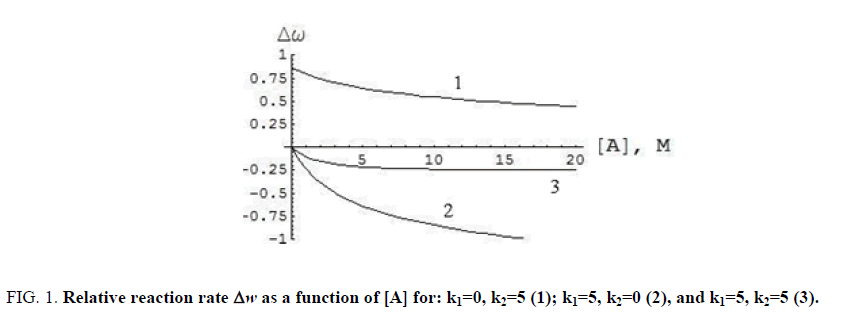
Rate constant w was found to depend on k1, k2, and monomer/dimer ratio (FIG. 1). The influence of acoustic wave with angular frequency ω=2πv was calculated from formula (5) under the assumption that equilibrium constant Kν(t) can be used as averaged value Kav:
Figure 1: Relative reaction rate Δw as a function of [A] for: k1=0, k2=5 (1); k1=5, k2=0 (2), and k1=5, k2=5 (3).
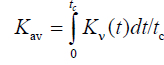 , (6)
, (6)
Where tc=(2πν)-1 is the period of action. The dependence of relative reaction rate Δw on [A] is exemplified in FIG. 1. Here Δw=(w-wν)/w, where wν is reaction rate (4) at K0=0.2, K=Kav (6), ω=18.84 s-1, and P0=15.
As follows from FIG. 1, the reaction kinetics is defined by the reactivity of monomers and dimers. The reaction rate increases when the reactivity of dimers is higher than that of monomers, and vice versa. From FIG. 1 it is visible that the reaction does not depend on a ratio of rate constants k1 and k2 and also reaches an extreme value at high concentrations. The influence of mechanical action depends on its amplitude and is independent of its frequency. The connection of chemical reaction rate and concentration of reagents with parameters of wave mechanical influence (amplitude, oscillation frequency) also depends on the kinetic scheme of reaction and supra-molecular structure of reagents (quantity and type of associates).
This work was financially supported by FASO (grant 0089-2014-0021).
References
- Smirnov LP, Kulagina TP. Features of the kinetics of chemical reactions in a nanostructured liquid. Russ J Phys Chem B. 2017;11:786-97.
- Kononov LO. Chemical reactivity and solution structure: on the way to a paradigm shift? RSC Adv. 2015;5:46718-34.
- Ganiev RF, Fomin VN, Malyukova EB, et al.; Wave Treatment of Latex-Based Disperse Systems. Dokl Chem. 2005;403:164-67.
- Chegodaev NA, Kulagina TP, Smirnov LP. Influence of acoustic vibrations on the kinetics and mechanism of first-order chemical reactions in nanostructured liquid phase, paper presented at Fourth International Scientific Conference, PFUR, Moscow, Russia. 2017;2111.
- Kulagina TP, Smirnov LP, Andrianova ZS. Mathematical simulation of low-frequency mechanical action on bimolecular reaction kinetics in a structured liquid. J Phys Chem B. 2018;12:657-62.