Original Article
, Volume: 17( 2)General Properties of the Balances 2âÂÂf (O)-f (H) Related to Electrolytic Systems
- *Correspondence:
- Tadeusz Micha?owski, CHASP, Department of Analytical Chemistry, Cracow University of Technology, Warszawska, Poland, Tel: +48126282035; E-mail: michalot@o2.pl
Received: November 16, 2017; Accepted: December 04, 2017; Published: December 09, 2017
Citation: Micha?owska-Kaczmarczyk AM, Spórna-Kucab A, Micha?owski T. General Properties of the Balances 2?f (O) – f (H) Related to Electrolytic Systems. Anal Chem Ind J. 2017;17(2):124
Abstract
The fundamental property of electrolytic systems, involved with linear combination 2∙f (O) – f (H) of elemental balances: f (H) for H and f (O) for O, is presented in terms of the Generalized Approach to Electrolytic Systems (GATES). The balance 2∙f (O) – f (H) is: (a) linearly dependent on charge balance (ChB) and other elemental and/or core balances f (Yj) (Yj ≠ H, O) related to a non-redox system, or (b) linearly independent on these balances, when related to a redox system. This dependency/independency property of 2∙f (O) – f (H) is the general criterion distinguishing between non-redox and redox systems, of any degree of complexity. It clearly explains why the balances: f (H) and f (O and then 2∙f (O) – f (H) are not formulated for non-redox systems. For a redox system, 2∙f (O) – f (H) is the primary form of Generalized Electron Balance (GEB), formulated according to Approach II to GEB and considered as the fundamental/indispensable equation needed for resolution of electrolytic redox systems according to GATES/GEB principles. These general properties are proved in the related examples and extended on other systems. The paper provides simple regularities that enable to check the dependency/independency criterion and formulate the GEB for redox systems.
Keywords
Redox and non-redox electrolytic systems; Linear combination
Introduction
Any electrolytic system is a kind of thermodynamic system, perceived as the macroscopic part of the universe selected for observation and experimentation [1]. For modeling purposes, we assume a closed system, separated from the environment by diathermal walls, preventing any exchange of a matter between the system and its environment, but allowing the exchange of heat between them. A temperature change occurring in the system as a result of exo- or endothermic transformations may influence the equilibrium constants values and, therefore, the system must be kept under isothermal conditions, ensured by diathermal walls during quasistatic processes occurring therein.
Thermodynamics of electrolytic systems embodies fundamental principles/laws. In order to balance a particular electrolytic system, we use two physical laws of conservation, namely: law of charge conservation and law of conservation of particular elements/cores. Law of charge conservation is expressed by charge balance (ChB). The law of elements/cores conservation interrelate particular elements/cores in components forming a system and the species formed in the system in the balances: f (H)for Y1=H, f (O) for Y2=O and f (Yk) for Yk ≠ H, O, i.e., k=3,…, K. A core is a cluster of different atoms with definedchemical formula, structure and external charge that is unchanged in the system considered [2]; e.g. C2O4-2 and CO3-2 aredifferent cores, non-transformable in the system presented in Example 3.1, but transformable (C2O4-2 → CO3-2) in the systempresented in Example 3.2.
The charge and elemental balances are interrelated, but the effects of this interrelation look differently for non-redox and redox systems; the difference lies in linear dependence or independence of 2?f (O)-f (H) from ChB and f (Yk) for k=3,…, K. Obviously, such independency or dependency regularities occur also between the balances when expressed in terms of molar concentrations [mol/L] and denoted, per analogism, as CHB, 2?F (O)–F (H) and F (Yk) (k=3,…, K).
The balance 2?f (O)–f (H) is then a keystone differentiating between non-redox and redox electrolytic systems, of any degree of complexity [2-4]. When related to a redox system, 2?f (O)–f (H) is the primary form of the Generalized Electron Balance (GEB), 2?f (O)–f (H)=pr-GEB, formulated according to Approach II to GEB within the Generalized Approach to Electrolytic Systems (GATES), introduced/formulated (1992) by Michalowski [3]. The GEB is put in context with GATES; the resulting software is denoted as GATES/GEB [2-25].
The GEB is perceived as the law of matter conservation, as the law of Nature and the GATES/GEB is the best possible thermodynamic approach to redox systems. The GEB was discovered by Michalowski and formulated in totally mature forms: first as the Approach I (1992) [26-35] and then as the Approach II (2006) [2-25,36-48] to GEB. It should emphatically be stressed that both Approaches are equivalent, from a formal point of view.
∴ Approach II to GEB ↔ Approach I to GEB
In the Approach I to GEB, the knowledge of oxidation numbers is required, whereas in the Approach II to GEB the knowledge of oxidation numbers is not needed. Also the oxidizing and reducing components and species in a redox system are not explicitly specified/indicated; in other words, such a necessity does not exist there. This is a paramount advantage of the Approach II to GEB, especially in relation to complex chemical compounds and complex species formed in electrolytic systems, after dissolution of (mixtures of) these compounds in a properly chosen solvent, e.g. water.
Any prior knowledge of oxidation numbers for elements in components forming the redox system and in the species of the static or dynamic redox system thus formed is not required. The proper linear combination of f12=2?f (O)–f (H) with charge balance f0=ChB and other elemental and/or core balances fk=f (Yk) (k=3,…, K) expressed in terms of numbers of particular units: N0j for components forming a system and Ni for species formed in the system; it gives the identity 0=0 for non-redox systems. For a redox system, the proper linear combination of f12=2?f (O)–f (H) with f0=ChB and other elemental and/or core balances fk=f (Yk) (k=3,…, K) gives the simplest/shortest form of GEB.
In further discussion, we refer to chemical compounds, with defined chemical composition, formed from the elements, whose atoms/nuclei do not subject to radioactive (α, β-, β+) transformations/decay. Specific chemical compounds are used as components of an electrolytic system. After mixing these components, a mixture of defined species is formed.
We write the corresponding balances in a compact, unified form. For this purpose, we apply first the following notations: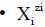 for the species as hydrates
for the species as hydrates 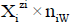 in aqueous (W=H2O) media, or
in aqueous (W=H2O) media, or 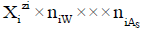 in S-solvent media [19-23], where zi=0, ± 1, ± 2,… is a charge, expressed in terms of elementary charge units, e=F/NA (F=Faraday’s constant, NA=Avogadro’s number); ni=( ≥ 0) is a mean number of H2O molecules attached to
in S-solvent media [19-23], where zi=0, ± 1, ± 2,… is a charge, expressed in terms of elementary charge units, e=F/NA (F=Faraday’s constant, NA=Avogadro’s number); ni=( ≥ 0) is a mean number of H2O molecules attached to 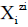 in aqueous media; niAS ≥ 0 (s=1,…, S)-mean number of As molecules attached to
in aqueous media; niAS ≥ 0 (s=1,…, S)-mean number of As molecules attached to  in S-solvent media;
in S-solvent media;
• The  ’s with different numbers of H2O molecules involved, e.g. H+1, H3O+1, H9O4+1 ; H4IO6-1, IO4-1 ; H2BO3-1, B(OH)4-1 ;AlO2-1, Al(OH)4-1 are also considered equivalently, i.e., as the same species, in this medium. Naturally, free water particles and water bound in hydrates, are included in the balances for f (H) and f (O);
’s with different numbers of H2O molecules involved, e.g. H+1, H3O+1, H9O4+1 ; H4IO6-1, IO4-1 ; H2BO3-1, B(OH)4-1 ;AlO2-1, Al(OH)4-1 are also considered equivalently, i.e., as the same species, in this medium. Naturally, free water particles and water bound in hydrates, are included in the balances for f (H) and f (O);
• J–number of kinds of different components forming the system, N0j-number of molecules of a component of j-th kind; 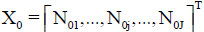 – vector of components;
– vector of components;
• I–number of different kinds of species formed in the system; Ni-number of the species of i-th kind: 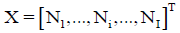 -vector of the species; N1–number of free W=H2O molecules; N2-number of H+1?n2W ions; N3-number of OH-1?n3W ions;
-vector of the species; N1–number of free W=H2O molecules; N2-number of H+1?n2W ions; N3-number of OH-1?n3W ions;
In this paper, the general regularities inherent in a proper choice of multipliers in the linear combinations are indicated. The term "proper" is used herein in terms of intended purposes. The first aim is to demonstrate here a linear relationship between the balances related to a non-redox system.
The second aim is to achieve the simplest/purposeful form of GEB on the basis of equations relating to a redox system. The primary objective is here to demonstrate that none combination of linear equations relating to a redox system is reducible to identity; this is also intended to demonstrate the equivalence between the Approaches I and II to GEB. The Approach I to GEB can be perceived in terms of ‘card game’ (FIG. 1 ), with electron-active elements as ‘players’, electron-non-active elements-as ‘fans’ and electrons-as ‘money’ [38].
The GEB obtained according to Approach I does not involve the species composed only of electron-non-active elements (‘fans’). The identity comes down to the cancellation of all the components of the equation obtained after formulating a linear combination of 2?f (O)–f (H) with the output equations related to ‘fan-elements’ or ‘fan-cores’. In 2?f (O)–f (H), all components involved with water molecules are cancelled, i.e. those involved with water as components (e.g. N06 in Example 3.1), as species (N1) and those in hydrates (ni) of the respective species.
Generalizing Notation and Linear Combination
The ChB has the common form 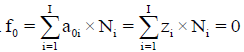 i.e., a0i=zi, related to the species
i.e., a0i=zi, related to the species 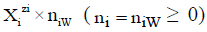 in aqueous (W=H2O) media, or to the species
in aqueous (W=H2O) media, or to the species 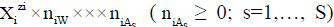 values in S-solvent media. Thus the components form a system; the species
values in S-solvent media. Thus the components form a system; the species 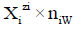 enter the system thus formed. Molar concentration of the species
enter the system thus formed. Molar concentration of the species 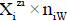 equals to
equals to 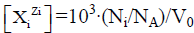 for a static system (V0), or
for a static system (V0), or 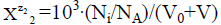 a dynamic D+T system.
a dynamic D+T system.
The ni=niW values are virtually unknown–even for 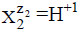 [40] in aqueous media and depend on ionic strength (I, mol/L) of the solution. The elemental/core balances: f (H), f (O) and f (Yk) (k=3,…, K) are written as follows:
[40] in aqueous media and depend on ionic strength (I, mol/L) of the solution. The elemental/core balances: f (H), f (O) and f (Yk) (k=3,…, K) are written as follows:
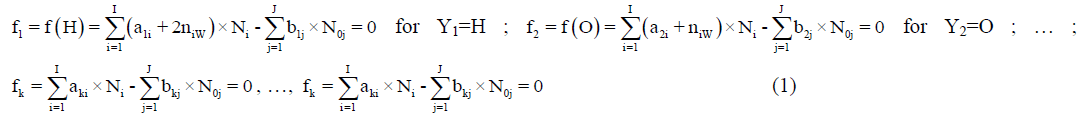
Where, aki and bkj are the numbers of atoms of k-th element/core in i-th species and j-th component, resp. Then the balance
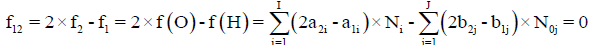 (2)
(2)
is formulated. The linear combination,
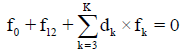
Is the sum of K balances: f0, f12, f3,…, fK. In these balances, the terms involved with water, i.e., N1, N0j (for j related to H2O as the component) and ni=niW are not involved. For the convenience of linear combination (avoiding possible/simple mistakes), we can apply the equivalent relations:
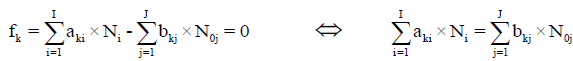
For elements with negative oxidation numbers, or
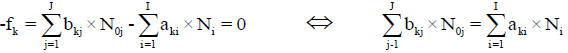
For elements with positive oxidation numbers.
All the balances considered below are presented explicitly, to check the validity of the reasoning and accept it without reservations. The paper is illustrated with plots related to some dynamic systems, where volume V [mL] of T is considered as a parameter of such systems, used in calculation procedure and realized according to iterative computer programs, e.g. MATLAB [3].
Methods
Non-redox systems
Example 1: V0 mL of a solution is obtained after mixing N01 molecules of H2C2O4 ?2H2O, N02 molecules of NaHCO3, N03 molecules of Na2CO3, N04 molecules of CH3COONa, N05 molecules of HCl and N06 molecules of H2O. The solution contains the following species: H2O (N1), H+1 (N2, n2), OH-1 (N3, n3), H2C2O4 (N4, n4), HC2O4-1 (N5, n5), C2O4-2 (N6, n6), H2CO3 (N7,n7), HCO3-1 (N8, n8), CO3-2 (N9, n9), Na+1 (N10, n10), CH3COOH (N11, n11), CH3COO-1 (N12, n12), Cl-1 (N13, n13). The ChB (Equation 4), elemental (equations 5-8) and core (equations 9-11) balances in the closed system are as follows:
f0=ChB
N2–N3–N5–2N6–N8–2N9+N10–N12–N13=0 (4)
f1=f (H)
2N1+N2 (1+2n2)+N3 (1+2n3)+N4 (2+2n4)+N5 (1+2n5)+2N6n6+N7 (2+2n7)+N8 (1+2n8)+2N9n9+2N10n10 +N11 (4+2n11)+N12 (3+2n12)+2N13n13=6N01+N02+3N04+N05+2N06 (5)
f2=f (O)
N1+N2n2+N3 (1+n3)+N4 (4+n4)+N5 (4+n5)+N6 (4+n6)+N7 (3+n7)+N8 (3+n8)+N9 (3+n9)+N10n10 +N11 (2+n11)+N12 (2+n12)+N13n13=6N01+3N02+3N03+2N04+N06 (6)
–f3=-f (Na)
N02+2N03+N04=N10 (7)
f4=f (Cl)
N13=N05 (8)
–f5=-f (C2O4)
N01=N4+N5+N6 (9)
–f6=-f (CO3)
N02+N03=N7+N8+N9 (10)
–f7=-f (C2H3O2)
N04=N11+N12 (11)
From equations 4–11, we obtain the linear combinations:
f12=2·f (O)–f (H)
– N2+N3+6N4+7N5+8N6+4N7+5N8+6N9+N13=6N01+5N02+6N03+N04–N05 (12)
2·f (O)–f (H)+ChB–f (Na)+f (Cl)–6·f (C2O4)– 4·f (CO3)– 0·f (C2H3O2)=0 (13)
0=0 (13a)
i.e., Equation 13 can be considered as identity, 0=0 (relation 13a), i.e., all numbers, related to components and species, on the left and right sides of the linear combination (13) are cancelled; it can be rewritten as follows:
(+1)·f (H)+(–2) · f (O)+(+1)·f (Na)+(–1)?f (Cl)+2·(+3)·f (C2O4)+1·(+4)·f (CO3) +2·(0) · f (C2H3O2)–ChB=0 (14)
From Equation 14 we see that the multipliers of the corresponding balances are the oxidation numbers of elements in the elemental balances, or the oxidation numbers (in round brackets) for elements ≠ H, O, multiplied by the numbers of atoms ≠ H, O of these elements in the corresponding cores.
It should be noticed that the oxidation number of C in CH3COOH (=C2H4O2=C2 (H2O)2) and in CH3COO-1 is equal zero (0); 2?x+3?(+1)+2?(–2)=–1 ? x=0; then the core balance f (C2H3O2) does not enter the linear combination of the balances.
Within the elemental balance for carbon C, i.e.,
F (C)=2?f (C2O4)+f (CO3)+2?f (C2H3O) 2N4+2N5+2N6+N7+N8+N9+2N11+2N12=2N01+N02+N03+2N04 (15)
We have the species with different oxidation degrees of C: +3, +4 and 0. Then the linear combination of 2·f (O)–f (H)+ChB–f (Na)+f (Cl) with f (C) does not give the identity, 0=0. Note that oxalate, carbonate and acetate species are not mutually transformable in this (non-redox) system and then the balances for f (C2O4), f (CO3) and f (C2H3O) can be presented separately (equations 9–11).
When applying the relations: 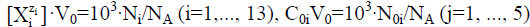 from equations 7–11 we have the balances expressed in terms of molar concentrations:
from equations 7–11 we have the balances expressed in terms of molar concentrations:
[Na+1]=C02+2C03+C04; [Cl-1]=C05; [H2C2O4]+[HC2O4-1]+[C2O4-2]=C01
[H2CO3]+[HCO3-1]+[CO3-2]=C02+C03; [CH3COOH]+[CH3COO-1]=C04
Involved in the identity relation
(+1)·F (H)+(–2)·F (O)+(+1)·F (Na)+(–1)?F (Cl)+2·(+3)·F (C2O4)+1·(+4)·F (CO3) +2·0·F (C2H3O)–CHB=0 (16)
From the identity (13) we obtain,
2·f (O)–f (H)=f (Na)–f (Cl)+6·f (C2O4)+4·f (CO3)+0·f (C2H3O)–ChB (17)
i.e., 2·f (O)–f (H) is the linear combination of ChB and elemental and core balances for elements/cores ≠ H, O. Analogously, from the identity (16) we have
2·F (O)–F (H)=F (Na)–F (Cl)+6·F (C2O4)+4·F (CO3)–CHB (18)
Example 2: In complexonometric (EDTA) titration of zinc [19], the titrant D is composed of N01 molecules of ZnSO4·7H2O, N02 molecules of NHM3, N03 molecules of NH4Cl, N04 molecules of NaH2In=C20H12N3O7SNa, N05 molecules of H2O and the titrant T is composed of N06 molecules of EDTA=Na2H2L·2H2O=C10H14N2O8Na2·2H2O and N07 molecules of H2O, at defined point of titration (V mL of T added). In the system in question, the following species are formed:
H2O (N1), H+1 (N2, n2), OH-1 (N3, n3), HSO4-1 (N4, n4), SO4-2 (N5, n5), Cl-1 (N6, n6), Na+1 (N7, n7), NH4+1 (n8, N8), NHM3 (n9, N9), Zn+2 (N10, n10), ZnOH+1 (N11, n11), soluble complex Zn(OH)2 (N12, n12), Zn(OH)3-1 (N13, n13), Zn(OH)4-2 (N14, n14), ZnNHM3+2 (N15, n15), Zn(NHM3)2+2 (N16, n16), Zn(NHM3)3+2 (N17, n17), Zn(NHM3)4+2 (N18, n18), ZnCl+1 (N19, n19); ZnSO4 (N20, n20), C20H13N3O7S (N21, n21), C20H12N3O7S-1 (N22, n22), C20H11N3O7S-2 (N23, n23), C20H10N3O7S-3 (N24, n24), C20H10N3O7SZn-1(N25, n25), (C20H10N3O7S)2Zn-4 (N26, n26), C10H18N2O8+2 (H6L+2) (N27, n27), C10H17N2O8+1 (H5L+1) (N28, n28), C10H16N2O8 (H4L) (N29, n29), C10H15N2O8-1 (H3L-1) (N30, n30), C10H14N2O82- (H2L-2) (N31, n31), C10H13N2O8-3 (HL-3) (N32, n32), C10H12N2O8-4 (L-4) (N33, n33), C10H13N2O8Zn-1 (ZnHL-1) (N34, N34), C10H12N2O8Zn-2 (ZnL-2) (N35, n35), C10H13N2O9Zn-3 (ZnOHL-3) (N36, n36).
These species are arranged in the following balances:
f0=ChB
N2–N3–N4–2N5–N6+N7+N8+2N10+N11–N13–2N14+2n15+2N16+2N17+2N18+N19–N22–2N23 –3N24–N25–4N26+2N27+N28–N30–2N31–3N32–4N33–N34–2N35–3N36=0 (19)
f1=f (H)
2N1+N2(1+2n2)+N3(1+2n3)+N4(1+2n4)+2N5n5+2N6n6+2N7n7+N8(4+2n8)+N9(3+2n9)+2N10n10 +N11(1+2n11)+N12(2+2n12)+N13(3+2n13)+N14(4+2N14)+N15(3+2n15)+N16(6+2n16)+N17(9+2n17) +N18(12+2n18)+2N19n19+2n20n20+N21(13+2n21)+N22(12+2n22)+N23(11+2n23)+N24(10+2n24) +N25(10+2n25)+N26(20+2n26)+N27(18+2n27)+N28(17+2n28)+N29(16+2n29)+N30(15+2n30) +N31(14+2n31)+N32(13+2n32)+N33(12+2n33)+N34(13+2N34)+N35(12+2n35)+N36(13+2n36) =14N01+3N02+4N03+12N04+2N05+18N06+2N07
f2=f (O)
N1+N2n2+N3(1+n3)+N4(4+n4)+N5(4+n5)+N6n6+N7n7+N8n8+N9n9+N10n10+N11(1+n11)+N12(2+n12) +N13(3+n13)+N14(4+n14)+n15n15+N16n16+N17n17+N18n18+N19n19+N20(4+n20)+N21(7+n21)+N22(7+n22) +N23 (7+n23)+N24 (7+n24)+N25 (7+n25)+N26 (14+n26)+N27 (8+n27)+N28 (8+n28)+N29 (8+n29)+N30 (8+n30) +N31 (8+n31)+N32 (8+n32)+N33 (8+n33)+N34 (8+N34)+N35 (8+n35)+N36 (9+n36) =11N01+7N04+N05+10N06+N07
f12=2·f (O)–f (H)
–N2+N3+7N4+8N5–4N8–3N9+N11+2N12+3N13+4N14–3n15–6N16–9N17–12N18+8n20+N21 +2N22+3N23+4N24+4N25+8N26–2N27–N31+N30+2N31+3N32+4N33+3N34+4N35+5N36 =8N01–3N02–4N03+2N04+2N06 (20)
f3=f (Cl)
N6+N21=N03 (21)
– f4=-f (Na)
N04+2N06=N7 (22)
– f5=-f (SO4)
N01=N4+N5+N20 (23)
f6=f (NHM3)
N8+N9+N16+2N17+3N18+4N19=N02+N03 (24)
– f7=-f (Zn)
N01=N10+N11+N12+N13+N14+N15+N16+N17+N18+N19+N20+N21+N22+N34+N35+N36 (25)
f8=f (C20H12N3O7S)
N21+N22+N23+N24+N25+2N26=N04 (26)
f9=f (C10H12N2O8)
N27+N28+N29+N30+N31+N32+N33+N34+N35+N36=N06 (27)
Then we have, by turns,
2·f (O)–f (H)+ChB+f (Cl)–f (Na)–6·f (SO4)+3·f (NHM3)–2·f (Zn)–f (C20H10N3O7S) – 0·f (C10H12N2O8)=0 (28)
(+1)?f (H)+(–2)·f (O)+(–1)·f (Cl)+(+1)·f (Na)+(+6)·f (SO4)+(–3)·f (NHM3)+(+2)·f (Zn)+(+1)·f (C20H10N3O7S) +0·f (C10H12N2O8)–ChB=0 (29)
Since the terms related to components and species on the left side of the equations 28 and 29 are cancelled, it follows that the relations: 28 and then 29 express the identity, 0=0, that testifies about linear dependence between the balances, i.e., Equation 29 is linearly dependent on other balances in the system:
2·f (O)–f (H)=–f (Cl)+f (Na)+6·f (SO4)–3·f (NHM3)+2·f (Zn)+f (C20H10N3O7S) (30)
From Equation 29 we see that the multipliers of the equations for the corresponding simple ions are equal to the oxidation numbers: +1 for H+1, –1 for Cl-1, +1 for Na+1. The multipliers for f (O), f (SO4) and f (NHM3) are equal to oxidation numbers: –2 for O, +6 for S in SO4-2 and –3 for N in NHM3. As refers to H3In=C20H13N3O7S=C20N3S(H2O)6OH, we have x–2+1=0), i.e. x=1 for C20N3S. For C10N2 in H4L=C10H16N2O8=C10N2(H2O)8 we have x=0.
Equations 23, 24, 26, 27 are specified separately, according to different “cores”: SO4-2, NHM3, C20H10N3O7S-3 and C10H12N2O8-4. Note that N enters the compounds and species in equations 26, 27; S enters the compounds and species in equations 23, 26; C enters the compounds and species in equations 26, 27. However, none transformations occur between the “cores” of the species that belong to different core balances. Generalizing, for any non-redox system, there are some numbers/multipliers for the relevant equations that reduce the sum received to the identity, 0=0.
Referring again to Equation 26, related to the species involved with erio T, one can write the elemental balances: 20N23+20N24+20N25+20N26+20N27+40N28=20N04 (for C), 3N23+3N24+3N25+3N26+3N27+6N28=3N04 (for N), N23+N24+N25+N26+N27 +2N28=N04 (for S) and 7N23+7N24+7N25+7N26+7N27+14N28=7N04 (for O). All the equations are equivalent to equation 26, because the “core” C20H10N3O7S is unchanged in reactions occurred during the titration. Similarly, the species involved with EDTA (Equation 27), fulfill the relations: 10N29+10N31+10N32+10N33+10N34+10N35+10N36+10N37+10N38+10N39=10N06 (for C) and 3N29+3N31+3N32+3N33+3N34+3N35+3N36+3N37+3N38+3N39=3N06 (for N); both equations are equivalent to Equation 27.
Redox systems
Example 3.1: V0 mL of D composed of FeSO4?7H2O (N01 molecules), H2SO4 (N03 molecules) and H2O (N05 molecules) is titrated with V mL of T composed of KMnO4 (N06 molecules) and H2O (N08 molecules). In V0+V mL of the D+T mixture thus formed we have the following species: H2O (N1), H+1 (N2, n2), OH-1 (N3, n3), HSO4-1 (N4, n4), SO4-2 (N5, n5), K+1 (N6, n6), Mn+2 (N7, n7), MnOH+1 (N8, n8), MnSO4 (N9, n9), Mn+3 (N10, n10), MnOH+2 (N11, n11), MnO4-2 (N12, n12), MnO4-1 (N13, n13), Fe+2 (N14, n14), FeOH+1 (N15, n15), FeSO4 (N16, n16), Fe+3 (N17, n17), FeOH+2 (N18, n18), Fe(OH)2+1 (N19, n19), Fe2(OH)2+4 (N20, n20), FeSO4+1 (N21, n21), Fe(SO4)2-1 (N22, n22).
It is also assumed here that the solution is sufficiently acidified with H2SO4, to prevent formation of MnO2 precipitate in the system; the same remark is also obligatory in Example 3.2 (below). The balances for this system are as follows:
f0=ChB
N2–N3–N4–2N5+N6+2N7+N8+3N10+2N11–2N12–N13+2N14+N15+3N17+2N18+N19 +4n20+N21–N22=0 (31)
f1=f (H)
2N1+N2 (1+2n2)+N3 (1+2n3)+N4 (1+2n4)+2N5n5+2N6n6+2N7n7+N8 (1+2n8)+2N19n9+2N10n10 +N11 (1+2n11)+2N12n12+2N13n13+2N14N14+N15 (1+2n15)+2N16n16+2N17n17+N18 (1+2n18)+N19 (2+2n19) +N20 (2+2n20)+2n21n21+2N22n22=14N01+2N03+2N05+2N08
f2=f (O)
N1+N2n2+N3 (1+n3)+N4 (4+n4)+N5 (4+n5)+N6n6 +N7n7+N8 (1+n8)+N9 (4+n9)+N10n10+N11 (1+n11) +N12 (4+n12)+N13 (4+n13)+N14N14+N15 (1+n15)+N16 (4+n16)+N17n17+N18 (1+n18)+N19 (2+n19)+N20 (2+n20) +N21 (4+n21)+N22 (8+n22)=11N01+4N03+N05+4N06+N08
f12=2?f (O)–f (H)
–N2+N3+7N4+8N5+N8+8N9+N11+8N12+8N13+N15+8N16+N18+2N19+2n20+8n21+16N22 =8N01+6N03+8N06 (32)
– f3=-f (K): N06=N6 (33)
– f4=-f(S)=-f (SO4): N01+N03=N4+N5+N9+N16+N21+2N22 (34)
f5=f (Fe): N14+N15+N16+N17+N18+N19+2n20+N21+N22=N01 (35)
f6=f (Mn): N7+N8+N9+N10+N11+N12+N21=N06 (36)
The linear combination, composed from balances for electron-non-active elements (‘fans’ [2,5,39]), has the form
2?f (O)–f (H)+ChB–f (K)–6?f (SO4)=0 (37)
2(N14+N15+N16)+3(N17+N18+N19+2n20+N21+N22)+2(N7+N8+N9)+3(N10+N11)+6N12+7N13 =2N01+7N06 (37a)
The simplest form is represented by the balance:
2?f (O)– f (H)+ChB–f (K)–6?f (S)–3?f (Fe)–2?f (Mn)=0 (38)
N10+N11+4N12+5N13–(N14+N15+N16)=5N06–N01 (38a)
As we see, Equation 38a, as the simplest form of the linear combination related to this system, is different from identity 0=0. Multiplying equations 38 and 38a by –1, we have:
(+1)?f (K)+(+6) ?f (SO4)+(+3)?f (Fe)+(+2)?f (Mn)+(–2)?f (O)+(+1)?f (H)–ChB=0 (39)
N14+N15+N16–(5N13+4N12+N10+N11)=N01–5N06 (39a)
Applying the relations:
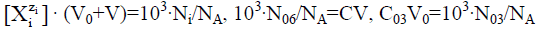 (40)
(40)
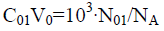 (40a)
(40a)
We reconsider it as the titration of V0 mL of FeSO4 (C01)+H2SO4 (C03)+CO2 (C04) solution as D with V mL of KMnO4 (C)+CO2 (C1) solution as T. Then from Equation 39a we have [11,30]
[Fe+2]+[FeOH+1]+[FeSO4]-(5[MnO4-1]+4[MnO4-2]+[Mn+3]+[MnOH+2])=(C01V0-5CV)/(V0+V) (41)
It is the simplest/shortest form of GEB related to this system, expressed in terms of concentrations. It is obtained from linear combination of the balances as specified in Equation 39, where the multipliers applied are equal to the oxidation numbers of the corresponding elements in the species present in this system.
Denoting atomic numbers of Fe and Mn by ZFe=26 and ZMn=25, from equations 35, 36 and 37a we get the balance
ZFe ?f (Fe)+ZMn ?f (Mn)-(2?f (O)-f (H)+ChB+f (K)+6?f (S))=0 (42)
(ZFe–2)(N14+N15+N16)+(ZFe–3) (N17+N18+N19+2n20+N21+N22)+(ZMn–2) (N7+N8+N9)+ (ZMn–3)(N10+N11)+(ZMn–6) N12+(ZMn–7) N13=(ZFe–2) N01+(ZMn–7) N06 (42a)
Then, from equations 42a, 40, 40a one obtains the relation
(ZFe–2)([Fe+2]+[FeOH+1]+[FeSO4])+(ZFe–3)([Fe+3]+[FeOH+2]+[Fe(OH)2+1]+2[Fe2(OH)2+4]+[FeSO4+1]+[ Fe(SO4)2-1])+(ZMn–2)([Mn+2]+[MnOH+1]+[MnSO4])+(ZMn–3)([Mn+3]+[MnOH+2])+(ZMn–6)[MnO42-]+(ZMn–7)[MnO4-]=(ZFe–2)C01V0+(ZFe–7)CV)/(V0+V)
Identical with GEB obtained immediately according to Approach I to GEB. From equations 33-36, 40, 40a we have the balances:
[H+1]-[OH-1]-[HSO4-1]-2[SO4-2]+[K+1]+2[Mn+2]+[MnOH+1]+3[Mn+3]+2[MnOH+2]-2[MnO4-1]+2[Fe+2]+[FeOH+1]+3[Fe+3]+2[FeOH+2]+[Fe (OH)2+1]+4[Fe2(OH)2+4] [FeSO4+1]-[Fe(SO4)2-1]=0 (32a)
[K+1]=CV/(V0+V) (33a)
[HSO4-1]+[SO4-2]+[MnSO4]+[FeSO4]+[FeSO41]+2[Fe (SO4)2-1]=(C01+C03) V0/(V0+V) (34a)
[Fe+2]+[FeOH+1]+[FeSO4]+[Fe+3]+[FeOH+2]+[Fe (OH)2+1]+2[Fe2(OH)2+4]+[FeSO4+1]+[Fe(SO4)2-1]=C01V0/(V0+V) (35a)
[Mn+2]+[MnOH+1]+[MnSO4]+[Mn+3]+[MnOH+2]+[MnO4-2]+[MnO4-1]=CV/(V0+V) (36a)
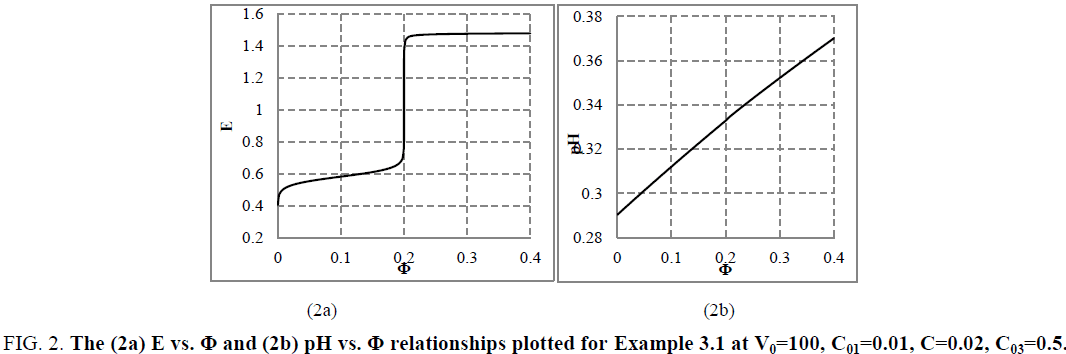
The relation (33a) is considered as equality (from mathematical viewpoint), because-for defined C, V0 and V values-it is a number and enters, as such, the CHB (Equation 32a). The GEB (Equation 41 or Equation 43), CHB (Equation 32a) and k=3 concentration balances (equations 34a, 35a, 36a) form a set of 2+k=5 independent balances with 5 independent scalar variables forming the vector x=[E, pH, pSO4, pFe3, pMn2]T, where E-potential, pH=–log[H+1], pSO4=–log[SO4-2], pFe2=–log[Fe+2], pMn2=–log[Mn+2]. Other species inherent in the system are expressed by these variables in terms of the related equilibrium constants, collected in [11]. On the basis of calculations related to this system we obtain the curves: E=E (Φ) (FIG. 2a ) and pH=pH (Φ) (FIG. 2b ), where [11].
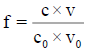
Figure 2: The (2a) E vs. Φ and (2b) pH vs. Φ relationships plotted for Example 3.1 at V0=100, C01=0.01, C=0.02, C03=0.5.
Example 3.2: V0 mL of titrant D, composed of N02 molecules of H2C2O4·2H2O, N03 molecules of H2SO4, N04 molecules of CO2 and N05 molecules of H2O, is titrated with V mL of titrant T composed of KMnO4 (N06), CO2 (N07), H2O (N08). In this mixture, the following species are formed: H2O (N1); H+1 (N2, n2), OH-1 (N3, n3), HSO4-1 (N4, n4), SO4-2 (N5, n5); K+1 (N6, n6),Mn+2 (N7, n7), MnOH+1 (N8, n8), MnSO4 (N9, n9), Mn+3 (N10, n10), MnOH+2 (N11, n11), MnO4-2 (N12, n12), MnO4-1 (N13, n13),H2C2O4 (N23, n23), HC2O4-1 (N24, n24), C2O4-2 (N25, n25); H2CO3 (N26, n26), HCO3-1 (N27, n27), CO3-2 (N28, n28), MnC2O4 (N29,n29), Mn (C2O4)2-2(N30,n30),Mn(C2O4)3-4(N31,n31),MnC2O4+1(N32,n32),Mn(C2O4)2-1(N33,n33),Mn(C2O4)3-3(N34, N34),MnC2O4 (N35, n35) (precipitate).
Applying the notations: 40 and
C02V0=103?N02/NA (40b)
We reconsider it as the titration of V0 mL of H2C2O4 (C02)+H2SO4 (C03)+CO2 (C04) solution as D with V mL of KMnO4 (C)+CO2 (C1) solution as T.
It is assumed here that CO2 in D and T originate from air, on the step of preparation of the related solutions, before titration. On the step of titration, CO2 is formed as the product of reaction 2MnO4-1+5H2C2O4+6H+1=2Mn+2+10CO2+8H2O. Formodeling purposes it is assumed that all CO2 is retained in the liquid phase, under the influence of externally applied pressure; in this phase CO2 is transformed in the forms of carbonic acid, mainly: H2CO3. Consequently, only the liquid phase (in general: the condensed phases) is included within the limits of this system. Admission of removing the excess of CO2 from the liquid phase invalidates the assumption of a closed system, which involves also the admission of H2O evaporation from the solution. The species in the closed system are involved in the following elemental balances:
f0=ChB
N2-N3-N4-2N5+N6+2N7+N8+3N10+2N11-2N12-N13-N24-2N25-N27-2N28-2N30-4N31 +N32-N33-3N34=0 (45)
f1=f (H)
2N1+N2 (1+2n2)+N3 (1+2n3)+N4 (1+2n4)+2N5n5+2N6n6+2N7n7+N8(1+2n8)+2N9n9+2N10n10 +N11 (1+2n11)+2N12n12+2N13n13+N23 (2+2n23)+N24 (1+2n24)+2N25n25+N26 (2+2n26)+N27(1+2n27)+2N28n28+2N29n29+2N30n30+2N31n31+2N32n32+2N33n33+2N34N34+2N35n35=6N02+2N03+2N05+2N08
f2=f (O)
N1+N2n2+N3 (1+n3)+N4 (4+n4)+N5 (4+n5)+N6n6+N7n7+N8 (1+n8)+N9 (4+n9)+N10n10 +N11 (1+n11)+N12 (4+n12)+N13 (4+n13)+N23 (4+n23)+N24 (4+n24)+N25 (4+n25)+N26 (3+n26)+N27 (3+n27) +N28 (3+n28)+N29 (4+n29)+N30 (8+n30)+N31 (12+n31)+N32 (4+n32)+N33 (8+n33)+N34 (12+N34)+N35 (4+n35) =6N02+4N03+2N04+N05+4N06+2N07+N08
f12=2?f (O)-f (H)
–N2+N3+7N4+8N5+N8+8N9+N11+8N12+8N13+6N23+7N24+8N25+4N26+5N27+6N28+8N29 +16N30+24N31+8N32+16N33+24N34+8N35=6N02+6N03+4N04+8N06+4N07 (46)
–f3=– f (K)
N06=N6 (47)
–f4=– f (SO4)
N03=N4+N5+N9 (48)
2?f (O)-f (H)+ChB-f (K)-6?f (SO4)
2N7+2N8+2N9+3N10+3N11+6N12+7N13+6N23+6N24+6N25+4N26+4N27+4N28+8N29+14N30 +20N31+9N32+15N33+21N34+8N35=6N02+4N04+7N06+4N07 (49)
–f5=– f (Mn)
N06=N7+N8+N9+N10+N11+N12+N13+N29+N30+N31+N32+N33+N34+N35 (50)
–f6=– f (C)
2N02+N04+N07=2N23+2N24+2N25+N26+N27+N28+2N29+4N30+6N31+2N32+4N33 +6N34+2N35 (51)
The linear combination
2?f (O)-f (H)+ChB-f (K)-6?f (SO4)-2?f (Mn)-4?f (C)=0 (52)
Can be transformed as follows:
N10+N11+4N12+5N13-2N23-2N24-2N25-2N29-4N30-6N31-N32-3N33-5N34-2N35=5N06-2N02 → 2(N23+N24+N25+N29+N35)+4N30+6N31+N32+3N33+5N34-(5N13+4N12+N10+N11)=2N02-5N06 → 2([H2C2O4]+[HC2O4-1]+[C2O4-2]+[MnC2O4]+[MnC2O4])+4[Mn C2O4)2-2]+6[Mn(C2O4)3-4]+[MnC2O4+1]+3[Mn (C2O4)2-1]+5[Mn (C2O4)3-3]-(5[MnO4-1]+4[MnO4-2]+[Mn+3]+[MnOH+2]) =(2C02V0-5CV)/(V0+V) (53)
Where, equations 40 and 40b are applied. Equation 52 can be rewritten as follows:
(+1)?f (H)+(–2) ?f (O)+(+1) ?f (K)+(+6) ?f (SO4)+(+2) ?f (Mn)+(+4) ?f (C)-ChB=0 (52a)
(+1)?F (H)+(–2) ?F (O)+(+1) ?F (K)+(+6) ?F (SO4)+(+2) ?F (Mn)+(+4) ?F (C)-CHB=0 (52b)
As we see, the receipt of the simplest form of GEB (Equation 53) requires the use of the multipliers at the corresponding balances (equations, equality) according to the rules assumed previously. Equation 53, as the simplest form of GEB for this redox system, is different from identity, 0=0. Eq. 50b is completed by Equation 33a, and:
[H+1]-[OH-1]-[HSO4-1]-2[SO4-2]+[K+1]+2[Mn+2]+[MnOH+1]+3[Mn+3]+2[MnOH+2]-2[MnO4-2] – [MnO4-1]-[HC2O4-1]-2[C2O4-2]-[HCO3-1]-2[CO3-2]-2[Mn(C2O4)2-2]-4[Mn(C2O4)3-4] +[MnC2O4+1]-[Mn (C2O4)2-1]-3[Mn(C2O4)3-3]=0 (45a)
[HSO4-1]+[SO4-2]+[MnSO4]=C03V0/(V0+V) (47a)
[Mn+2]+[MnOH+1]+[MnSO4]+[Mn+3]+[MnOH+2]+[MnO4-2]+[MnO4-1]+[MnC2O4]+[Mn(C2O4)2-2]+[Mn(C2O4)3-4]+[MnC2O4+1]+[Mn(C2O4)2-1]+[Mn(C2O4)3-3]+[MnC2O4]=CV/(V0+V) (49a)
2([H2C2O4]+[HC2O4-1]+[C2O4-2])+[H2CO3]+[HCO3-1]+[CO3-2]+2[MnC2O4]+4[Mn(C2O4)2-2] +6[Mn(C2O4)3-4]+2[MnC2O4+1]+4[Mn(C2O4)2-1]+6[Mn(C2O4)3-3]+2[MnC2O4] =(2C02V0+C04V0+C1V)/(V0+V) (50a)
Applying ZC=6 and ZMn=25, from (48)-(50) we obtain, by turns,
ZC?f (C)+ZMn? f (Mn)-(2?f (O)-f (H)+ChB-f (K)-6?f (SO4))=0 (53)
(ZMn-2)? (N7+N8+N9)+(ZMn-3) ? (N10+N11)+(ZMn-6)?N12+(ZMn-7)?N13+2(ZC-3)(N23+N24+N25) +(ZC-4) (N26+N27+N28)+(2ZC+ZMn-8) (N29+N35)+(4ZC+ZMn-14) N30+(6ZC+ZMn-20) N31+(2ZC+ZMn-9) N32 +(4ZC+ZMn-15) N33+(6ZC+ZMn-21) N34=2(ZC-3) N02+(ZC-4) (N04+N07)+(ZMn-7) N06 → (ZMn-2)? (N7+N8+N9)+(ZMn-3) ? (N10+N11)+(ZMn-6) ?N12+(ZMn-7) ? N13+2(ZC-3) (N23+N24+N25) +(ZC-4) (N26+N27+N28)+((ZMn-2)+2(ZC-3)) (N29+N35)+((ZMn-2) +4(ZC-3)) N30+((ZMn-2)+6(ZC-3)) N31 +((ZMn-3) +2(ZC-3)) N32+((ZMn-3) +4(ZC-3)) N33+((ZMn-3) +6(ZC-3)) N34 =2(ZC-3) N02+(ZC-4) (N04+N07)+(ZMn-7) N06
(ZMn-2)?([Mn+2]+[MnOH+1]+[MnSO4])+(ZMn-3)?([Mn+3]+[MnOH+2])+(ZMn-6)?[MnO4-2] +(ZMn-7)?[MnO4-1]+2(ZC-3)([H2C2O4]+[HC2O4-1]+[C2O4-2])+(ZC-4)([H2CO3]+[HCO3-1]+[CO3-2]) +((ZMn-2)+2(ZC-3)) ([MnC2O4]+[MnC2O4])+((ZMn-2)+4(ZC-3)) [Mn(C2O4)2-2] +((ZMn-2)+6(ZC-3)) [Mn(C2O4)3-4]+((ZMn-3)+2(ZC-3))[MnC2O4+1]+((ZMn-3)+4(ZC-3))[Mn(C2O4)2-1] +((ZMn-3)+6(ZC-3)) [Mn(C2O4)3-3]=(2(ZC-3)C02V0+(ZC-4)(C04V0+C1V)+C1V)+(ZMn-7)CV)/(V0+V)(54)
Equation 54 is identical with the GEB obtained for this system immediately according to Approach I to GEB, i.e., it testifies about equivalency of both Approaches (I and II) to GEB.
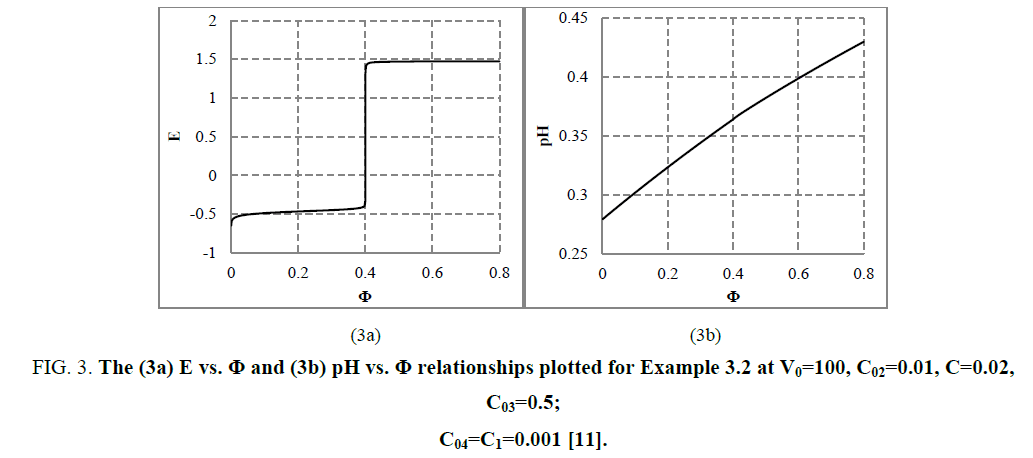
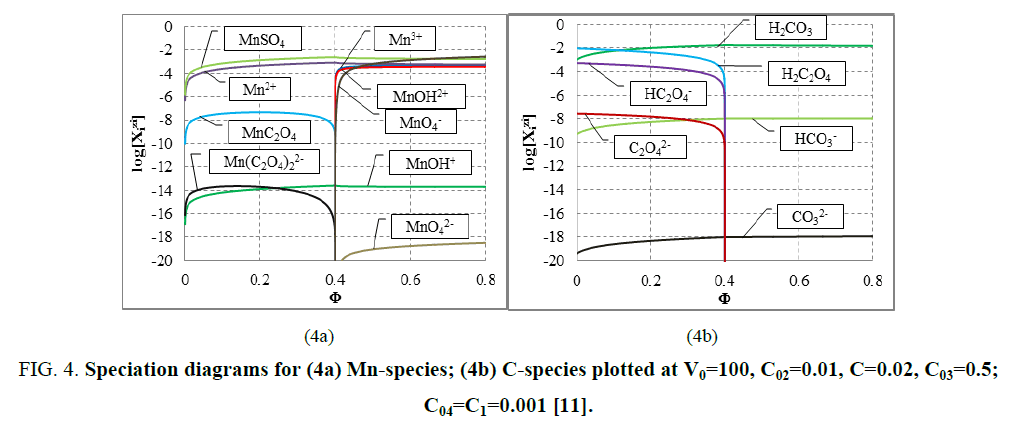
The E=E (Φ) and pH=Ph (Φ) plots and the speciation curves are presented in FIG. 3a,3b and FIG. 4a,4b , respectively.
Figure 3: The (3a) E vs. Φ and (3b) pH vs. Φ relationships plotted for Example 3.2 at V0=100, C02=0.01, C=0.02, C03=0.5; C04=C1=0.001 [11].
Figure 4: Speciation diagrams for (4a) Mn-species; (4b) C-species plotted at V0=100, C02=0.01, C=0.02, C03=0.5; C04=C1=0.001 [11].
Interrelations between concentrations of the species in balances presented in Examples 3.1, 3.2 were formulated on the basis of equilibrium constants, collected in [11].
The relations for equivalence volumes (Veq): CVeq=0.2?C0V0 for iron and CVeq=0.4?C02V0 for oxalate agree exactly with Φ-values where potential E jumps (FIG. 2a , 3a ) and abrupt changes in concentrations of some species occur (FIG. 4a,4b ).
Results and Discussion
Some remarks on the oxidation number and stoichiometry concepts
The oxidation number (ON), known also as oxidation state (OS), indicates the degree of oxidation of an atom in a chemical compound or a species. The semantic divagations between ON and OS still appear in [50]. The esoteric (but less scientific) ‘climate’ of OS reflects quite accurately the contents of the link [51], where the OS: (a) is defined as the charge of an atom that might be imagined to have when electrons are counted according to an agreed-upon set of well-defined, easy to follow rules (specified therein) [52]; (b) does not represent the real charge on the atom; (c) is the hypothetical charge that an atom would have if all bonds with atoms of different elements were 100% ionic, with no covalent component, i.e., after ionic approximation of bonds used: “The OS of a bonded atom equals its charge”, as is stated in [53,54]. The sign of the ionic approximation is commonly obtained on the basis of electronegativity’s of other atoms in the compound or species [55]. The more electronegative element acquires the negative charge and the less electronegative one acquires the positive charge. Consequently, it is stated that the assignment of electrons between atoms in calculating the oxidation state is purely formalism [51].
In the relevant definition, the specifying term "formal" is frequently used. In the dictionary of synonyms for "formal", one can find its optional meanings [56]: authentic, true, existing, concrete, undeniable, proven, licensed, approved, legal, legalized, legally approved, nominal. This term has also unambiguous connotations with “formal” potentials, perceived as a kind of conditional equilibrium constants (in the Ringworm sense) [57], where all side (unknown, in principle) reactions are involved, see critical remarks in [10]. In this context, it should be necessarily recalled that normal (not formal) potentials are used in GATES/GEB.
In essence, the oxidation number is a contractual concept, often awkward in interpretation, especially in relation to organic compounds. Here is revealed the great advantage of the Approach II to GEB, especially in relation to complex organic species, e.g. pigments (anti-oxidants) [58-62]. It should be recalled again that oxidation degree is-in essence-a contractual term that can be perceived within GATES/GEB as a derivative concept; for example, the Fe oxidation degree (+2, +3) in nitroprusside anion, Fe(NO)(CN)5-2, was not resolved for decades. The stoichiometry is also derivative concept in terms ofGATES and GATES/GEB.
As were stated above, the more extensive (but very simple!) derivation of GEB according to Approach II has an advantage over the Approach I to GEB that the Approach II does not require knowledge of oxidation degrees of elements in complex organic species. For practical needs, it is sufficient to apply GEB obtained on the basis of pr-GEB. Further linear combinations presented in the text were done only to prove the equivalency of the Approaches I and II to GEB.
The procedure involved with formulation of 2?f (O)-f (H) enables to formulate ON in chemical compounds and species both for non-redox and redox systems. The ON values for simple ions and according to Approach II to GEB, treats the valence of elements in chemical compounds and species as a derivable (not primary) concept.
In the fourteenth century, William of Ockham has formulated the parsimony (economy of thinking) principle that”entities should not be multiplied unnecessarily'' (“Pluralitas non est ponenda sine neccesitate''), known briefly as “Ockham’s razor”.
In reference to science, it means that simpler theories are generally better than more complex ones. GATES, based on fundamental rules of the matter conservation, acts according to the Ockham razor principle.
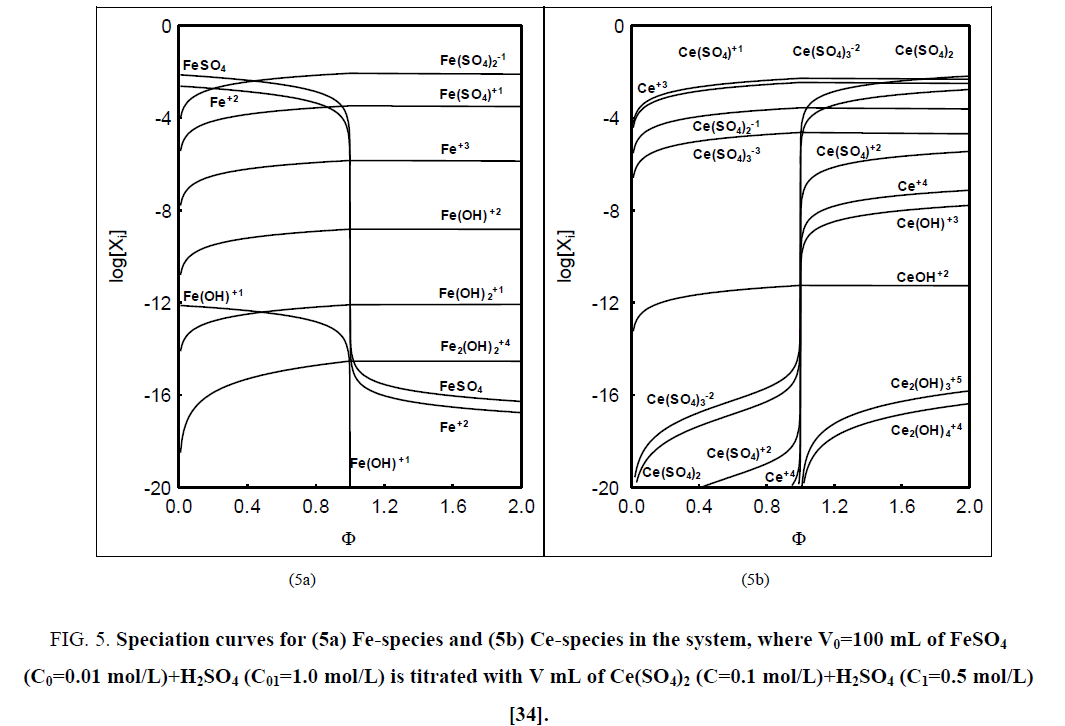
Referring to the balancing of electrolytic systems one can state that there is an important reason justifying the balancing of numbers (N0i, Ni) of entities (components, species), not masses of these entities; it is involved mainly with isotopic effects. The current practice observed in the relevant chemical literature issued hitherto indicates that the concept of a chemical reaction is treated by other authors equivalently with the notation of stoichiometric reaction, as stated in [9]. What's more, it is commonly stated elsewhere, that the equation of chemical reaction reflects the mass conservation principle. However, the reaction notation involves a few, frequently minor species of the system; e.g. in the system where (acidified, H2SO4) solution of FeSO4 is titrated with (acidified, H2SO4) solution of Ce (SO4)2 we have 29 species [34], whereas in the reaction notation Fe+2+Ce+4=Fe+3+Ce+3 there are involved only 4 minor species of the system (see FIG. 5a, 5b ). The value of the fraction titrated (Equation 44) at the equivalence (eq) point, Φ=Φeq=1, does not correspond to [Ce+3]=[Fe+3], see remarks in [34].
Figure 5: Speciation curves for (5a) Fe-species and (5b) Ce-species in the system, where V0=100 mL of FeSO4 (C0=0.01 mol/L)+H2SO4 (C01=1.0 mol/L) is titrated with V mL of Ce(SO4)2 (C=0.1 mol/L)+H2SO4 (C1=0.5 mol/L) [34].
Final comments
The generalized electron balance (GEB) concept, applied for electrolytic redox systems within GATES/GEB, is fully compatible with charge (ChB) and elemental/core balances f (Yg) and enables to resolve the electrolytic (mono- or/and two-phase) redox systems of any degree of complexity, within the scope of generalized approach to electrolytic redox systems (GATES/GEB). In any redox system, ChB, GEB and concentration balance(s) form the set of linearly independent algebraic equations. In other words, GEB is fully compatible balance in this set of balances.
GATES is the thermodynamic approach to equilibrium and metastable systems and gives the possibility to involve all physicochemical knowledge on the systems tested in the algorithm applied for calculation purposes. Possibilities of GATES/GEB are far greater than the actual physicochemical knowledge related to the system in question is offered.
The advantages of GATES were illustrated on examples of redox and non-redox systems presented in authors’ papers cited therein. GATES should be perceived as the unrivalled tool applicable, among others: (a) in mathematical modeling of the systems, (b) in choice of optimal a priori conditions of chemical analyses and (c) in gaining chemical information invisible in real experiments, in general. Furthermore, GATES is the basis for generalized equivalence mass (GEM) concept [16], considered as the advantageous alternative against the recommended/obligatory equivalence mass (EM) concept suggested by IUPAC and based on the chemical reaction notation. According to GATES, any chemical reaction notation is only a basis to formulate the related expression for equilibrium constant according to mass action law.
Within GATES one can resolve/simulate electrolytic systems of any degree of complexity, with use of all admissible physicochemical knowledge involved in it. One can follow the reactions in non-equilibrium systems [42] and pathways inaccessible in metastable systems [3-62]. In calculations, the metastable state is realized through omission of potential products in the related balances, whereas ‘unlocking’ a reaction pathway in metastable state is based on insertion of possible (from equilibrium viewpoint) products in the related balances. The interference effects, of different kind, can be also tested.
The electrolytic systems where all four kinds of basic (acid-base, redox, complexation, precipitation) chemical reactions occur simultaneously or sequentially were resolved according to GATES/GEB [3-44]. One can provide some examples, e.g. one in [27], where the fifth kind of equilibria, namely liquid-liquid extraction, is also involved. What is more, each kind of basic reaction, e.g. complexation, can be represented by different ligands. Four-step analytical process, where the four kinds of reactions are involved, was presented in [11,25].
This way, GATES/GEB provides a new, profound thermodynamic analysis of mono-, two- and three-phase (solution+solid phase+liquid-liquid) systems, of any degree of complexity. It is the new, advantageous alternative against other approaches known hitherto, represented e.g. by Pourbaix diagrams. All the principles realised within GATES can briefly be termed as an “escape into algebra”, where the “rachitic” chemical reaction equations are superseded by the firm system of algebraic equations [39]. The superiority of mathematical over purely chemical inferences is an indisputable matter. This conviction is the leading leitmotiv for GATES. The calculation procedure appears none problems when an effective, iterative computer program, e.g. MATLAB [3], be applied.
Conclusion
The GATES/GEB, presented in the review articles issued recently, is perceived as the cornerstone of scientific approach to electrolytic redox systems. GATES and GATES/GEB in particular, relies on the fact that the chemistry involved is predictable on the basis of knowledge on physicochemical properties of the species involved in the system in question. Referring to the motto put at the start of this paper, the physicochemical data obtained from the independent experiments form the stones embedded in a solid construction created by the set of compatible balances. The complete set of independent equilibrium constants interrelate concentrations of the species in the related equations.
References
- Gokcen NA, Reddy RG. Thermodynamics. 2nd ed. Plenum Press, New York. 1996.
- Micha?owska-Kaczmarczyk AM, Micha?owski T. Comparative balancing of non-redox and redox electrolytic systems and its consequences. Am J Analyt Chem. 2013;4(10):46-53.
- Micha?owski T. Application of GATES and MATLAB for resolution of equilibrium, metastable and non-equilibrium electrolytic systems. In: Applications of MATLAB in Science and Engineering. InTech. 2011.
- Micha?owski T, Micha?owska-Kaczmarczyk AM, Toporek M. Formulation of general criterion distinguishing between non-redox and redox systems. Electrochimica Acta. 2013;112:199-211.
- Micha?owski T, Toporek M, Micha?owska-Kaczmarczyk AM, et al. New trends in studies on electrolytic redox systems. Electrochimica Acta. 2013;109:519-31.
- Micha?owska-Kaczmarczyk AM, Toporek M, Micha?owski T. Speciation diagrams in dynamic iodide+dichromate system. Electrochimica Acta. 2015;155:217-27.
- Toporek M, Micha?owska-Kaczmarczyk AM, Micha?owski T. Symproportionation vs. disproportionation in bromine redox systems. Electrochimica Acta. 2015;171:176-87.
- Micha?owska-Kaczmarczyk AM, Micha?owski T, Toporek M. Formulation of dynamic redox systems according to GATES/GEB principles. Int J Electrochem Sci. 2016;11:2560-78.
- Micha?owska-Kaczmarczyk AM, Asuero AG, Micha?owski T. “Why not stoichiometry” vs. “Stoichiometry: Why not?” Part I: General Context. Crit Rev Anal Chem. 2015;45(2):166-88.
- Micha?owska-Kaczmarczyk AM, Micha?owski T, Toporek M, et al. “Why not stoichiometry” vs. “Stoichiometry: Why not?” Part III: Extension of GATES/GEB on Complex Dynamic Redox Systems. Crit Rev Anal Chem. 2015;45(4):348-66.
- Micha?owski T, Ponikvar-Svet M, Asuero AG, et al. Thermodynamic and kinetic effects involved in the pH titration of As (III) with iodine in a buffered malonate system. J Solution Chem. 2012;41(3):436-46.
- Micha?owski T, Pietrzyk A. The generalized electron balance concept. Derivation based on elementary rules of the matter conservation. Chemometrics: Methods and applications. Kraków. 2006:415-22.
- Micha?owski T, Pietrzyk A. Complementarity of physical and chemical laws of preservation in aspect of electrolytic systems. Przemys? Chemiczny. 2007;61:625-40.
- Micha?owski T. The generalized approach to electrolytic systems: I. Physicochemical and analytical implications.
Crit Rev Anal Chem. 2010;40(1):2-16. - Micha?owski T, Pietrzyk A, Ponikvar-Svet M, et al. The generalized approach to electrolytic systems: II. The generalized equivalent mass (GEM) concept. Crit Rev Anal Chem. 2010;40(1):17-29.
- Micha?owska-Kaczmarczyk AM, Micha?owski T. GATES as the unique tool for simulation of electrolytic redox and non-redox systems. J Anal Bioanal Tech. 2014;5(4):1-5.
- Toporek M, Micha?owska-Kaczmarczyk AM, Micha?owski T. Disproportionation reactions of HIO and NaIO in static and dynamic systems. Am J Analyt Chem. 2014;5(15):1046.
- Micha?owska-Kaczmarczyk AM, Micha?owski T. Linear dependence of balances for non-redox electrolytic systems. Am J Analyt Chem. 2014;5(17):1285.
- Micha?owska-Kaczmarczyk AM, Rymanowski M, Asuero AG, et al. Formulation of titration curves for some redox systems. Am J Analyt Chem. 2014;5(13):861.
- Micha?owska-Kaczmarczyk AM, Micha?owski T. Compact formulation of redox systems according to GATES/GEB principles. J Anal Sci. 2014;4(02):39.
- Micha?owska-Kaczmarczyk AM, Micha?owski T. Generalized electron balance for dynamic redox systems in mixed-solvent media. J Anal Sci. 2014;4(04):102.
- Micha?owski T, Pilarski B, Asuero AG, et al. Modeling of acid-base properties in binary-solvent systems. pp: 623-648.
- Micha?owska-Kaczmarczyk AM, Micha?owski T. General relation valid for electrolytic systems. J Anal Sci. 2015;5(4):74.
- Micha?owska-Kaczmarczyk AM, Micha?owski T, Toporek M, et al. Solubility and dissolution in terms of generalized approach to electrolytic systems principles. J Anal Sci. 2015;5(4):47.
- Michalowski T. Calculation of pH and potential E for bromine aqueous solution. J Chem Educ. 1994;71(7):560.
- Michalowski T, Lesiak A. Acid-base titration curves in disproportionation redox systems. J Chem Educ. 1994;71(8):632.
- Michalowski T, Lesiak A. Formulation of generalized equations for redox titration curves. Chemia Analityczna. 1994;39(5):623-37.
- Michalowski T, Wajda N, Janecki D. An unified quantitative approach to electrolytic systems. Chemia Analityczna. 1996;41:667-86.
- Micha?owski T, Baterowicz A, Madej A, et al. Extended Gran method and its applicability for simultaneous determination of Fe (II) and Fe (III). Analytica Chimica Acta. 2001;442(2):287-93.
- Micha?owski T. Calculations in analytical chemistry with elements of computer programming. Technical University of Cracow, Cracow. 2001.
- Micha?owska-Kaczmarczyk AM, Spórna Kb A, Micha?owski T. Principles of titrimetric analyses according to generalized approach to electrolytic systems (GATES). In: Advances in Titration Techniques 2017. InTech. 2017.
- Micha?owski T, Toporek M, Rymanowski M. Overview on the Gran and other linearization methods applied in titrimetric analyses. Talanta. 2005;65(5):1241-53.
- Micha?owski T, Kupiec K, Rymanowski M. Numerical analysis of the Gran methods: A comparative study. Analytica Chimica Acta. 2008;606(2):172-83.
- Ponikvar M, Micha?owski T, Kupiec K, et al. Experimental verification of the modified Gran methods applicable to redox systems. Analytica Chimica Acta. 2008;628(2):181-9.
- Micha?owski T, Pietrzyk A. Complementarity of physical and chemical laws of preservation in aspect of electrolytic systems. Wiadomo?ci Chemiczne. 2007;61:625-40.
- Micha?owski T. Generalized Electron Balance (GEB) as a Law of Preservation for Electrolytic Redox Systems.
- Micha?owska-Kaczmarczyk AM, Spórna-Kucab A, Micha?owski T. Generalized electron balance (GEB) as the law of nature in electrolytic redox systems. In: Redox-Principles and Advanced Applications 2017. InTech. 2017.
- Micha?owska-Kaczmarczyk AM, Spórna-Kucab A, Micha?owski T. A Distinguishing feature of the balance 2? f (O) − f (H) in electrolytic systems: The reference to titrimetric methods of analysis. In: Advances in Titration Techniques 2017. InTech. 2017.
- Micha?owska-Kaczmarczyk AM, Spórna-Kucab A, Micha?owski T. Solubility products and solubility concepts. In: Descriptive Inorganic Chemistry Researches of Metal Compounds 2017. InTech. 2017.
- Meija J, Micha?owska-Kaczmarczyk AM, Micha?owski T. Redox titration challenge. Anal Bioanal Chem. 2017;409(1):11-3.
- Micha?owski T, Micha?owska-Kaczmarczyk AM, Meija J. Solution to redox titration challenge. Anal Bioanal Chem. 2017;409(17):4113-5.
- Micha?owska-Kaczmarczyk AM, Spórna-Kucab A, Micha?owski T. A General Property Differentiating Between Redox and Non-Redox Electrolytic Systems and Its Consequences.
- Micha?owska-Kaczmarczyk AM, Spórna-Kucab A, Micha?owski T. Principles of titrimetric analyses according to generalized approach to electrolytic systems (GATES). In: Advances in Titration Techniques 2017. InTech. 2017.
- Micha?owska-Kaczmarczyk AM, Spórna-Kucab A, Micha?owski T. Formulation of simple electrolytic redox systems According to GATES/GEB Principles. Korean J Chem Eng. 2017.
- Karen P, McArdle P, Takats J. Toward a comprehensive definition of oxidation state (IUPAC Technical Report). Pure Appl Chem. 2014;86(6):1017-81.
- Karen P, McArdle P, Takats J. Comprehensive definition of oxidation state (IUPAC Recommendations 2016). Pure Appl Chem. 2016;88(8):831-9.
- Pauling L. The modern theory of valency. J Chem Soc. (Resumed). 1948:1461-7.
- Ringbom A. Complexation in Analytical Chemistry. Interscience Publishers; New York. 1963.
- Pietrzkowski Z, Nemzer B, Spórna A, et al. Influence of betalain-rich extract on reduction of discomfort associated with osteoarthritis. New Med. 2010;1:12-7.
- Nemzer B, Pietrzkowski Z, Spórna A, et al. Betalainic and nutritional profiles of pigment-enriched red beet root (Beta vulgaris L.) dried extracts. Food Chem. 2011;127(1):42-53.
- Wybraniec S, Micha?owski T. New pathways of betanidin and betanin enzymatic oxidation. J Agr Food Chem. 2011;59(17):9612-22.
- Wybraniec S, Stalica P, Spórna A, et al. Antioxidant activity of betanidin: Electrochemical study in aqueous media. J Agr Food Chem. 2011;59(22):12163-70.
- Wybraniec S, Starzak K, Skopin?ska A, et al. Studies on nonenzymatic oxidation mechanisms in neobetanin, betanin and decarboxylated betanins. J Agr Food Chem. 2013;61(26):6465-76.
- Wybraniec S, Starzak K, Skopi?ska A, et al. Effects of metal cations on betanin stability in aqueous-organic solutions. Food Sci Biotechnol. 2013;22(2):353-63.
- Wasielewska E. Sindo studies on reactivity of [M (CN) 5NO] n − complex ions for M=Fe, Mn, Cr. Inorganica Chimica Acta. 1986;113(2):115-7.
- Stochel G, Stasicka Z, Brindell M, et al. Bioinorganic photochemistry. John Wiley & Sons; 2009.
- Giovangigli V. Multicomponent flow modeling. Modeling and Simulation in Science, Engineering and Technology.
- de Levie R. A simple expression for the redox titration curve. J Electronal Chem. 1992;323(1-2):347-55.
- Micha?owski T, Pietrzyk A. A thermodynamic study of struvite+water system. Talanta. 2006;68(3):594-601.
- Micha?owski T, Pietrzyk A. Quasistatic processes in non-equilibrium two-phase systems with ternary salts: I. Struvite+Aqueous solution (CO2+KOH). Chemia Analityczna. 2008;53(1):33-46.
- Michalowski T, Asuero AG. Thermodynamic modelling of dolomite behavior in aqueous media. J Electronal Chem. 2012.
- Micha?owski T, Rymanowski M, Pietrzyk A, et al. Non-typical Brönsted’s acids and bases. J Chem Educ. 2005;82(3):470-472.