Original Article
, Volume: 13( 2)Assessment of Mutual Information Based Least Dependent Component Analysis in Comparison with Fast ICA for Blind Source Separation of Images
- *Correspondence:
- Parimala Gandhi A , Department of ECE, KIT-Kalaignarkarunanidhi Institute of Technology, Coimbatore, Tamil Nadu, India, Tel: 0422 236 7890; E-mail: parimalagandhi@yahoo.com
Received: March 09, 2017; Accepted: March 28, 2017; Published: March 30, 2017
Citation: Parimala Gandhi A, Vijayan S. Assessment of Mutual Information Based Least Dependent Component Analysis in Comparison with Fast ICA for Blind Source Separation of Images. Biotechnol Ind J. 2017;13(2):132.
Abstract
Blind source separation (BSS) is the process of separating the source signals from the combined observation signals without having any idea of the source signals as well as the method of combination. Though many methods are now emerging, based on performance and quality of separated signals MILCA (mutual information based least dependent component analysis) method has its outstanding capability with better separation quality and signal to noise ratio (SNR). Its main drawback which we have analyzed is that the time taken for separation of sources is very high compared to any other existing methods. It is normally in terms of hours when the number of source signals increases. Particularly when the number of source images goes beyond 9 or 10, it takes even a day for separation of all the images in which case all other methods take time just in terms of hours. One more observation we made is when the number of sources is increased, the performance of MILCA method becomes worse compared to other methods. So, the MILCA method is preferable one who is so picky about the separation quality and SNR. Instead of considering the ordinary images if the medical images like scanned images of any of the human body parts, EEG, ECG, MEG and Photographs of medical images can also be considered and BSS concepts can be applied for retrieving a clear and diagnosable images for further analysis about the diseases.
Keywords
Blind source separation (BSS); Independent component analysis (ICA); Fast independent component analysis (fast ICA); Mutual information based least-dependent component analysis; Processing time
Introduction
In many of the signal processing based applications, nowadays it is necessary to retrieve the message signals which are called source signals from a mixture of signals. Blind source separation is the only existing method for this purpose. Since in most of the cases, there won’t be any prior information regarding the source signals and the way of combination of the signals. Since without prior knowledge about the signals we are able to separate the sources, this process is called as ‘Blind Source Separation’. There are many number of blind source separation (BSS) techniques which are emerging in recent times. Among all the available methods, Independent Component Analysis (ICA) plays the main role as it is advanced compared to any existing methods. We apply some of the conditions on the source signals such as they are statistically independent, Gaussian, Non-Negative, etc. according to our requirement and convenience. BSS techniques have many numbers of applications in the fields like communication, audio signal processing, multimedia and image processing that too particularly in medical image processing which assures recovery of clear images for the proper diagnosis of diseases.
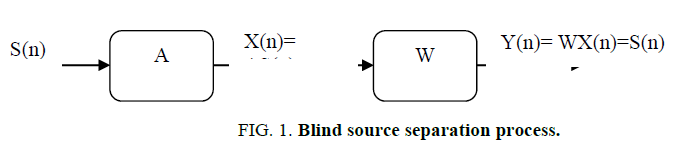
In mathematical terms the BSS problem can be expressed as,
X(n) = A*S(n) + N(n) (1)
Where, X(n) is the observed or mixed signal matrix from which sources are to be separated. A is a mixing matrix and S(n) is the source signal matrix. Here N(n) is the noise signal matrix. In the initial stage itself the noise removal is be done or in some cases the noise signal is not considered. So, with source separation techniques the sources are recovered as
Y(n) = W*X(n) (2)
i.e.,
Y(n) = W*A*S(n)= S(n) (3)
As the matrices A and W are inverse matrices to each other, the source signal S(n) can be retrieved since
W*A = I (4)
The process of Blind Source Separation can be explained with the following Figure. 1.
The major condition we apply to make the separation possible is that all the sources are statistically independent and possibly Gaussian.
This paper is organized in such a way that part II has the Literature survey, Part III is about the fast-independent component analysis (Fast ICA), Part IV has the details of mutual information based least-dependent component analysis (MILCA), Part V has the Comparison between Fast ICA and MILCA method performances in terms of result of BSS, Time consumption and Signal to Noise Ratio and finally Part VI is all about the future extension and conclusion of the work.
Literature Survey
Gandhi and Vijayan [1] included many number of possible operation on the images. These operations are based on different categories of operations such as Arithmetic operations, Logical operations, statistical operations, etc. This gives complete basics about the image processing operations and all the given possible operations can be carried over any type of images like medical images which are normally highly correlated, images taken by satellites, images available with communication systems etc. which are less correlated compared to the medical images.
Plumbley [2] proposed algorithm for non-negative independent component analysis. In this paper, the mean square error for ICA is minimized by using axis pair rotation and geodesic algorithm. Also, the various geometry considerations are derived by geodesic search approach. The image separation problem in fast convergence of the rotation and geodesic methods are also explained. But, this algorithm does not produce zero error when bias is added during data generation.
Bronstein et al. [3] provided the sparse ICA method for achieving the blind separation of broadcasted and reflected images. In this paper, the sparse ICA method is extended for concerning the issue of separating the image not including any prior information regarding its structure. The modern approaches in sparse ICA are investigated. This technique mostly utilized in different combinations of source images however the convolution of this method is complicated and it is not easy for all type of signals.
Mustafi and Ghorai [4] proposed blind source separation method by means of fractional Fourier transform for denoising medical images. This proposed method gives improved visual transparency to experts for utilizing the images during diagnosis. This method is also used for eliminating the most important component of additive or multiplicative noise from obtained image. Denoising the images without the knowledge about noise PDF is performed by using genetic algorithm and Gaussian filtering method. This method has better performance but the observation in time domain is very complex because of the fractional analysis with the images under frequency domain.
Benahmed et al. [5] presented the estimation of direction of arrival (DOA) based blind source separation for smart antenna. This method is used to direct the antenna radiation pattern towards the required radio frequency emitter. The different antenna patterns are observed and separated by using discrete Fourier transform model. ICA based separation is provided to extract the independent components and mixing matrix. This method will not be effective in the presence of co-channel interference as the correlation will be much higher. Then also for medical images this method will not be suitable. If a set of less correlated signal set or image set is selected then this method can be very much applicable.
Fast independent component analysis
Almost all of the measured quantities (normally called as observed signals) are in mixed form of some set of quantities or signals (called as source signals) whereas these quantities will normally be mixed automatically without knowing information either on the mixing process and or the signals which are mixed. The main assumption used in the ICA technique is that the value of one signal cannot be calculated from the remaining signals, which shows their independence nature [6-8].
ICA method of Blind Source Separation (BSS) process has found many application areas starting from cocktail party problem; it extends to EEG, MEG data analysis and finally to the complete biomedical applications.
If we consider the source signals as 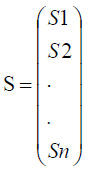 (5)
(5)
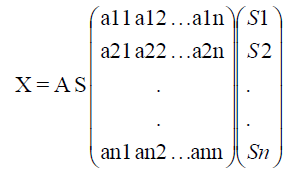
Also it can be taken as S=S1S2..Sn (the transposed form of S).If the mixture signal set is
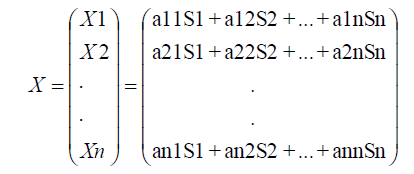 (6)
(6)
 (7)
(7)
Here
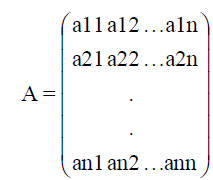 is called as mixing matrix whose value is unknown.
is called as mixing matrix whose value is unknown.
A is the matrix with mixing coefficients. The mapping between X to S is done through the unmixing matrix W which is a matrix with unmixing coefficients so that the unmixing process results in the source signals set S. Hence the effect of mixing process is equalized by unmixing matrix W and returning back the original signal where it is possible when the Matrices A and W are inverse matrices to each other. Since without knowing the mixing matrix A, calculation of W is done and S is obtained back, we cannot assure that W=A-1. We can state the unmixing process result as Y=W X. While verifying the results we can know about that Y=S and hence we can conclude that mixing and unmixing matrices are inverse matrices to each other.
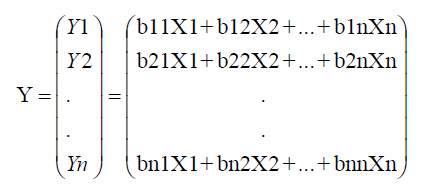 (8)
(8)
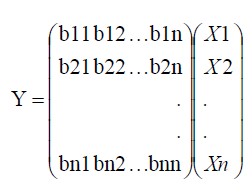 (9)
(9)
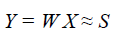 (10)
(10)
From the above observations, we can say W=A-1 which leads for source separation process. ICA is the method, perhaps the most widely used, for performing blind source separation. In many of the cases the effect of noise is omitted for convenience.
Mutual information based least-dependent component analysis
Next blind source separation (BSS) Technique is Mutual Information based least dependent component analysis (MILCA) which is the very competent technique among all the existing methods of BSS. In this method minimization of mutual information is done and the independency is analyzed based on their least value of mutual information. Now We explain this approach here, and will prove that it leads to the same principle of finding most non-Gaussian components. In particular, this approach gives a meticulous justification for the heuristic principles used previously.
Using the conception of differential entropy, the mutual information I between n (scalar) random variables is defined as,Let Yi, i=1...n, be n number of random variables. The mutual information between these random variables are defined as follows,
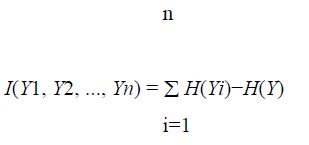 (11)
(11)
Mutual information (MI) is an accepted measure of the dependency between any two random variables. In detail, it is equivalent to find the correlation between these variables and we can know the common or similar information among them. If the selected variables are statistically independent, then the MI is always non-negative and possibly zero. Hence, the mutual information acquires into account the whole dependency structure of the included variables, and not only with covariance where PCA and related methods use.
Mutual information can be taken by using the entropy as code length. The terms H(Yi) give the lengths of these codes for the Yi where these are coded separately, and H(Y) gives the code length when Y is coded as a random vector instead of random variable, i.e. all the components are coded using the same code. Mutual information finally proves that code length reduction is obtained by coding the whole vector instead of the separate components. Generally, better codes can be attained by coding the whole vector. But, if the Yi are independent, then they won’t give information about each other, and one can code the variables separately without increasing their code length.
Now, consider what happens if we restrain the Yi to be uncorrelated and to have unit variance. i.e.,
E{YYT} =W E{XXT } WT = I, which implies that
| I | = 1 = (| W E{XXT } WT |) = (| W |)(| E{XXT })(| WT |) (12)
that denotes | W | must be constant. Moreover, for Yi of unit variance, entropy and negentropy are differing only by a constant and sign. Thus, we have,
I (Y1, Y2, ..., Yn) = C−Σ I (Yi) (13)
Where C is a constant which is independent of W. This gives the original relation between negentropy and the mutual information.
Mutual information based ICA
Since mutual information is the original information based measure of the independence of random variables and always nonnegative, we can use it as the decisive factor for finding the Independent Components. In this approach, the calculation is useful and equivalent to find the directions in which the negentropy is maximized. More accurately, it is equivalent to find one dimensional subspaces such that the projection in those subspaces have maximum negentropy. Scrupulously it demonstrates that ICA estimation with minimization of mutual information is equivalent to maximizing the total value of non-gaussianities of the variables. The restriction of uncorrelatedness is not necessary, but it simplifies the computations considerably. As a result, the formulation of ICA as reduction of mutual information gives another meticulous justification of our more heuristically introduced idea in deciding maximally non-gaussian directions.
Comparison between Fast IcCA and MlILCA method performances
To analyze about the suitability of the method which we have to use for the BSS problem can be decided by the performance comparison, SNR comparison and the Time consumption comparison charts. In all these comparisons, we can observe that MILCA method is best among all existing BSS methods as it has high separable property. But if we consider them based on time consumption basis, we should select Fast ICA method. By the SNR value also we can prefer to follow MILCA method as it has higher SNR value compared to Fast ICA.
One more observation we can find is that whenever the number of sources used to have mixed or observation images increases, it leads to poor separable sources and finally we are able to have only unclear images as sources. When number of observations (number of mixed signals) is more than the number of sources then it is possible to have complete separated images. But here only less number of observation images has been used and separated sources are obtained. If the number of observation images is more it would have resulted in better separability and clear sources might be obtained.
Separation quality/Performance comparison
For this purpose, 5 different color images were used and after converting them into grayscale images they were used for finding the mixed or observation images. Then from the observation images of grayscale images the sources were separated which resulted in separated grayscale images and not the color images. Since the mixing and separation of color images are not possible easily, only grayscale images were considered here.
The following Figure. 2-5 show 5 source images and the resulted separated images by Fast ICA method and MILCA method respectively.
SNR Comparison
Signal-to-Noise Ratio (SNR) is given as,
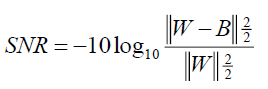 (14)
(14)
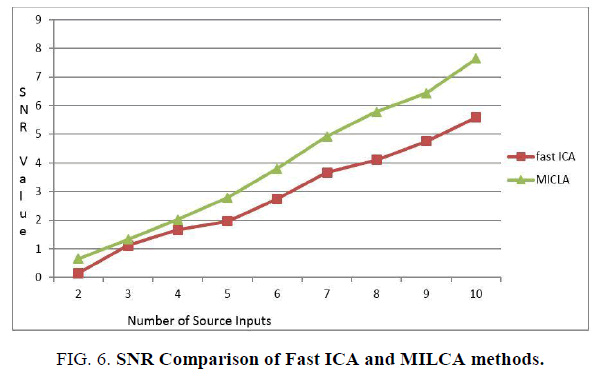
Figure. 6. shows the SNR comparison of Fast ICA and MILCA methods. It proves that irrespective of number of sources, MILCA method is the best available method in comparison with Fast ICA method.
Processing time comparison
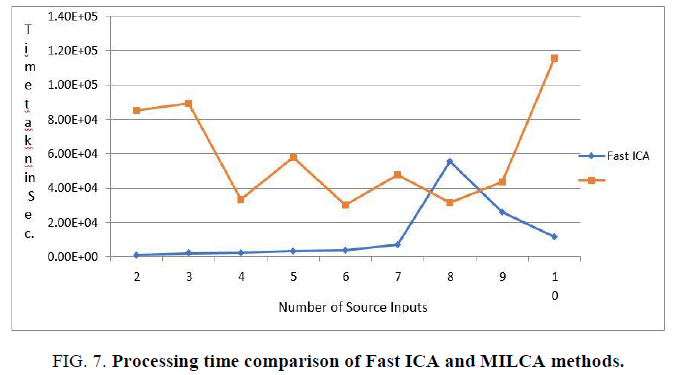
Processing time is the total time taken to separate the source signals when the observation images are given as mixed images with linearly independent nature.
Figure. 7. shows the SNR comparison of Fast ICA and MILCA methods. It proves that irrespective of number of sources, MILCA method is the best available method in comparison with Fast ICA method.
Future Extension and Conclusion
Here we considered only the images with less correlation or with linearly independence nature. In these above results, it is obvious that when MILCA method is selected, the separated image quality is high and only when the number of observation images are incomparable with the number of source images the quality of the separated images goes low. Otherwise whenever the number of sources are below 8 and the number of observation images are one the quality can be retained with this MILCA method. Based on processing time MILCA method is inferior to any other method like Fast ICA method. But if one is so specific about quality, processing time is secondary and it need not be taken as a constraint. If processing time is important then it is required to compromise on the separation quality of results.
As an extension of this work a newly framed algorithm can be combined with the concepts of MILCA method to overcome its drawback on processing time. The same can be implemented with medical signals which are highly correlated images compared to any other types of images.
References
- Parimala Gandhi A,Vijayan S. Various feasible maneuvers for the analysis of an image for retrieval of information and optimization. Int J Innovat Eng Techol. 2016;7(3):537-42.
- Plumbley. Algorithms for nonnegative independent component analysis. IEEE Trans Neural Networks. 2003;14(3):534-43.
- Bronstein AM, BronsteinMM, Zibulevsky M, et al. Sparse ICA for blind separation of transmitted and reflected images. Int J Imaging Syst Technol. 2005;15(1):84-91.
- Mustafi A, Ghorai SK. A novel blind source separation technique using fractional Fourier transform for denoising medical images. Optik.2013;124(3):265-71.
- Benahmed A, Zenkouar L, Hamzaoui E. DOA estimation for automatic steering of a smart antenna radiation pattern using the conventional ICA-based blind source separation method. In Proceedings of 2014 Mediterranean Microwave Symposium (MMS2014), IEEE. 2014; p.1-5.
- HyvarinenA. Independent component analysis: Recent Advances. Philos Trans A Math Phys Eng Sci. 2013; 371(1984):20110534.
- StogbauerH, KraskovA, AstakhovSA,et al. Least dependent component analysis based on mutual information. Phys Rev E. 2004;70:066123.
- Neumann-Institut für Computing [internet]. John von Neumann-Institut für Computing (NIC) [cited on: March 22, 2017], Available from: http://www.fz-juelich.de/nic/cs/software/