Original Article
, Volume: 12( 1)Transition Metals Doping Effects on Non-Linear Optical Properties of Be12O12 Nano-Cluster: A DFT Study
- *Correspondence:
- Shamlouei HR, Department of Chemistry, Lorestan University, Khorram Abad, Lorestan, I.R. Iran, Tel: 986633120618; E-mail: shamlouei.ha@lu.ac.ir
Received: July 09, 2017; Accepted: July 31, 2017; Published: August 09, 2017
Citation: Toosi AR, Shamlouei HR. Transition Metals Doping Effects on Non-Linear Optical Properties of Be12O12 Nano-Cluster: A DFT Study. Phys Chem Ind J. 2017;S1:103.
Abstract
Investigation about the effect of transition metal doping on structural, electronic, energetic, linear and nonlinear optical properties of Be12O12 nanocluster is the subject of this research. Results indicated that transition metals doping process leads to narrowing the energy gap (Eg) of them. Evidently the dipole moment and polarizability value of Be12O12 nanocluster increases because of that transition metals doping. The first hyperpolarizability value dramatically increases as substitute a magnesium atom with a transition metal atom. Among the transition metal atom doped nanocage, scandium has the largest first hyperpolarizability value (β◦ ≈ 4953 au). Also two-level model indicated that first hyperpolarizibility has severe dependence to excitation energies. The result of TD-DFT calculation indicates that the β0 has similar behavior as β2 which confirm the results of β0 obtained by ab initio calculation.
Keywords
Transition metals; Be12O12; Doping; NLO; Nanocage; First hyperpolarizability
Introduction
Due to the great applications, compounds with high nonlinear optical properties in the fields of optoelectronic and photonic devices, especially generation of optical harmonics, the scientists were attracted to investigate about m`aterial with high NLO properties [1-7]. There are many effective agents for enhancing the NLO properties such as: Electron donor and recipient groups, establishment of electron II, doping atom and etc. in original molecule [8-11]. Discovery of carbon nanotube [12] made a significant revolution in science and technology of nanomaterials. Scientists became interested to explore their new types of nanomaterial with unique properties and different functionalities. It has been shown that homologues of fullerene molecules have excellent applications in electronic devices, imaging materials, magnetic recording, and environmental processes; so, their investigation will be very interesting [13-16]. Theoretically, it is shown that, between different types of (XY)n structures, the nanocages with the general formula of (XY)12 have the most stable clusters [17-20] which employ in various application. To enhance the NLO properties of X12Y12 nanoclusters many efforts were done [21,22]. Recently, the effect of transition metals atoms doping on geometric, electronic, linear and nonlinear optical properties of Mg12O12 nanocage was investigated and it was shown that the first hyperpolarizability of Mg12O12 nanoclusters significantly enhanced through doping with transition metal atoms [23]. In present study, in the similar way, the effect of transition metal doping on Be12O12 nanocluster was studied. Calculation of the energies of the singlet excited states using time-dependent density functional (TD-DFT) method is the benefit of this research in comparison of previous research.
Computational Details
In this paper, all theoretical computations were done using density functional theory (DFT) with Gaussian 09 package [24]. All optimization calculations for considered nanocluster structures Be12O12 and Be11XO12 (X= transition metals atom) in ground state and excited state were calculated by B3LYP method in 6-31+g(d) basis set. Vertical energies of the singlet excited states were calculated using time-dependent density functional (TD-DFT) method at the B3LYP/6-31+g(d) level. The values of < S2> are 0.750 for a pure doublet and 0 for pure singlet systems, after spin annihilation. Recently has been developed for long-range interaction and charge transfer systems, a new density functional CAM-B3LYP [25,26] that can be useful for (hyper) polarizabilities calculations [27,28] and for considered nanocluster structures linear and non-linear optic properties and hyperpolarization were investigated.
We used CAM-B3LYP method in 6-31+g(d) level for determination of first hyperpolarizibility. The electronic properties of the considered nanocluster such as: the values of energies of HOMO (the highest occupied molecular orbital; EHOMO), LUMO (lowest unoccupied molecular orbital; ELUMO) and the energy gap (Eg) difference of between HOMO and LUMO levels as a critical parameter to determine molecular electrical transport properties investigated through their density of states (DOS) spectra obtained from GaussSum program [29].
The energy gap (Eg) is given as Eq. 1
Eg= E(HOMO) – E(LUMO) (1)
Where Eg is the energy gap, EHOMO and ELUMO are the values of energie of the highest and the lowest occupied molecular orbitals, respectively (in Ev).
The energy of an uncharged liner molecule in a weak and homogeneous external electric field can be defined as Eq. (2) [30,31].
E = E0-μαFα - 1/2 ααβFαFβ - 1/6 βαβγFαFβFγ -….. (2)
Where E0 is energy of system in zero electric field and Fα is the electric field component alongside α direction. μα, ααβ and βαβγ are the components of dipole moment, polarizability, and the first hyperpolarizability tensor.
The polarizability (α), first hyperpolarizability (β?) and tensor components of first hyperpolarizability (βijk) are noted as: [32,33]
α=1/3(αxx+αyy+αzz) (3)
β0 = (β x 2 + β y 2 + β z 2)1/2 (4)
In which βi= 3/5 (βiii + β ijj + βikk) i, j, k=x, y, z (5)
Where βijk (i, j, k = x, y, z) are tensor components of first hyperpolarizability.
Results and Discussion
In this research, at first all structures, Be12O12 and Be11XO12 (X= transition metals atom), were optimized then electronic properties, Polarizability (α) and first hyperpolarizability (β0) Be11XO12 were studied. For all doped nano clusters (Be11XO12), calculated excitation energy was compared with the first hyperpolarizibility in ground state.
Structural and energetic investigation
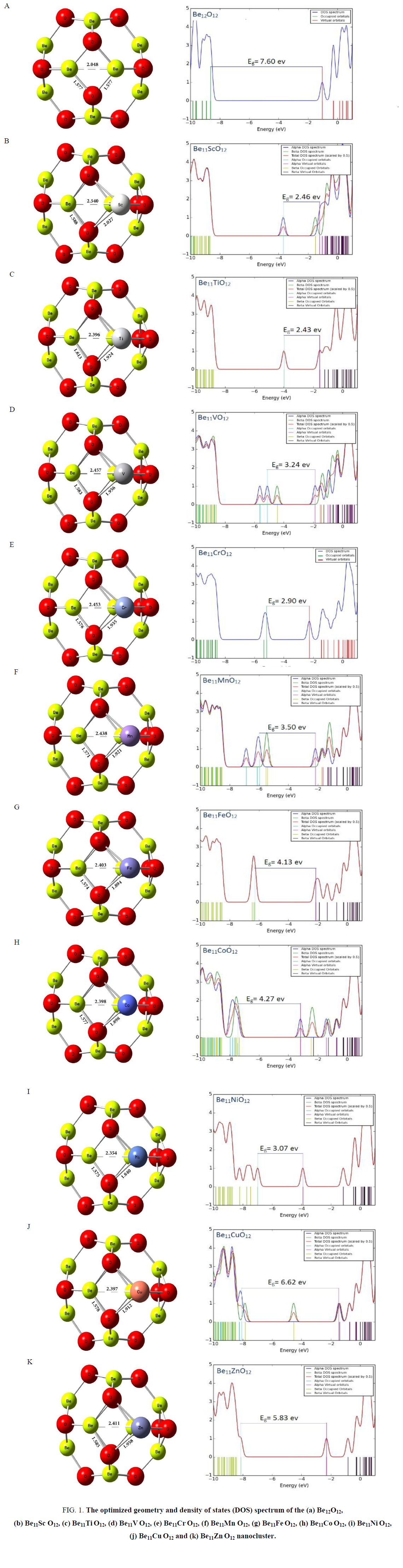
All structures, Be12O12 and Be11XO12 (X= transition metals atom), were optimized in the ground state by B3LYP method and in 6-31+g(d) basis set (Figure. 1). Be12O12 nanocluster consist of square and hexagon rings that alternatively the Be atoms connected to O atoms. The Be–O and Be–Be bonds length in square ring were analyzed for pure Be12O12.
Figure 1: The optimized geometry and density of states (DOS) spectrum of the (a) Be12O12, (b) Be11Sc O12, (c) Be11Ti O12, (d) Be11V O12, (e) Be11Cr O12, (f) Be11Mn O12, (g) Be11Fe O12, (h) Be11Co O12, (i) Be11Ni O12, (j) Be11Cu O12 and (k) Be11Zn O12 nanocluster.
The Be–O and Be–Be bonds length were calculated and obtained 1.577 and 2.048 angstrom in pure Be12O12, respectively. Then, one of the Beryllium atoms in square ring was substituted with transition metals atom and subsequent their structures were optimized. The optimized structures of the Be12O12 and doped nanoclusters with transition metals are presented in Figure. 1.
By doping transition metals atom in Be12O12 nanocluster, X–Be bond length in square ring increase and was compared to Be–Be bond length in pure Be12O12 and similar ring.
The variations maximum of bond length in among all of X-Be bonds appear for Sc-Be bond and Ni-Be bond length has the variations minimum; they were calculated 2.540 and 2.354 angstrom, respectively. Similarly, X-O bond length was increased for all doped atoms with transition metal.
The X–O, O-Be and X–Be bond length, O–X–O and O–Be–O bond angle in square ring, and doping energy for Be12O12 and doped nano cluster (Be11XO12) were gathered in TABLE. 1.
| Molecule | Bond length | Bond angle | E Be11XO12 | Edop | |||
|---|---|---|---|---|---|---|---|
| X-O | O-Be | X-Be | O-X-O | O-Be-O | |||
| Be12O12 | 1.577 | 1.578 | 2.048 | 98.211 | 98.199 | -1.72 | --- |
| Be11ScO12 | 2.027 | 1.588 | 2.54 | 77.346 | 105.86 | -2.91 | -5.87 |
| Be11TiO12 | 1.924 | 1.613 | 2.396 | 83.556 | 105.25 | -3.05 | -6.15 |
| Be11VO12 | 1.956 | 1.583 | 2.457 | 79.922 | 105.038 | -3.2 | -6.46 |
| Be11CrO12 | 1.935 | 1.576 | 2.453 | 79.777 | 103.827 | -3.36 | -6.78 |
| Be11MnO12 | 1.921 | 1.571 | 2.438 | 80.117 | 103.829 | -3.53 | -7.12 |
| Be11FeO12 | 1.894 | 1.574 | 2.403 | 81.719 | 103.841 | -3.71 | -7.47 |
| Be11CoO12 | 1.898 | 1.577 | 2.398 | 81.851 | 104.091 | -3.9 | -7.85 |
| Be11NiO12 | 1.84 | 1.575 | 2.354 | 82.745 | 101.078 | -4.1 | -8.25 |
| Be11CuO12 | 1.912 | 1.578 | 2.397 | 88.539 | 104.618 | -4.31 | -8.68 |
| Be11ZnO12 | 1.958 | 1.585 | 2.411 | 81.5 | 107.552 | -4.54 | -9.12 |
TABLE 1: X–O, O-Be and X–Be bond length (Angstrom), O–X–O and O–Be–O bond angle (degree) for square ring, EBe11XO12 (Kcal mol-1) and Edop (Kcal mol-1) for Be 12O12 and other doped nano cluster (Be11XO12).
The maximum value was assigned to Sc-O bond and minimum value was calculated for Ni-O bond. Owing to TABLE. 1 Be-O bond length in Be11XO12 was shown negligible changes. The O–Be–O angle was equal to 98.2 degree. The bond angles for all of doped Be12O12 nanocluster were decreased. The minimum decrement was assigned to O–Cu–O (88.539 degree) and maximum decrement occurs at O–Sc–O (77.346 degree).
The Be-X, Be-O and Be–Be bonds length and bond angles of O-X-O for square ring, are listed in TABLE 1 and depicted in Figure. 1.
Electronic properties
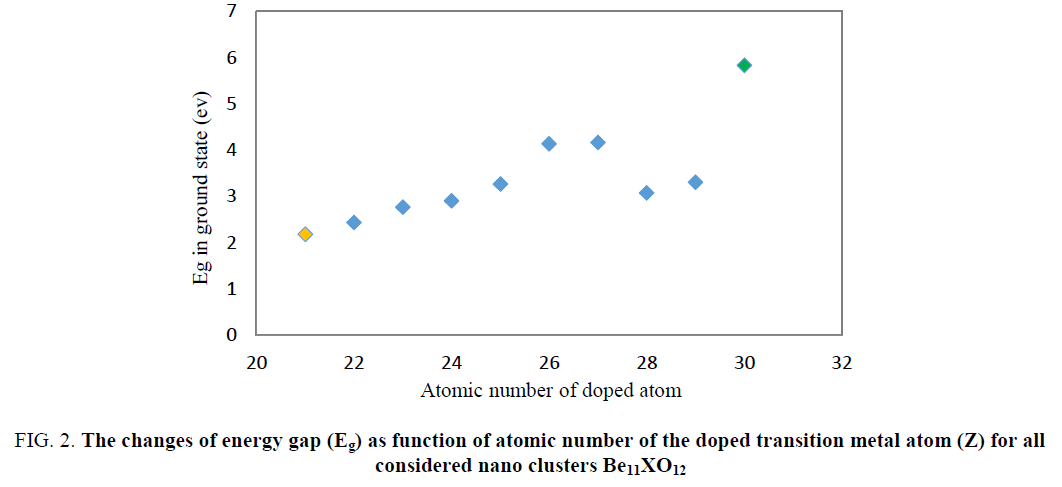
The obtained DOS spectrums are shown in Figure. 1. The Obtained EHOMO, ELUMO and Eg values from DOS spectrum (FIG. 1) are listed in TABLE 2. Energy gap for Be12O12 was about 7.60 ev (Be12O12 is an intrinsic semiconductor material because of large gap bond). As can be seen in TABLE 2, substitution 1 Be atom with 1 X atom (transition metals) in Be12O12 nanocluster leads to decreasing of HOMO-LUMO energy gap (Eg) so that it is transformed from an intrinsic semiconductor (Eg≈7.60 eV) to a p-type one (Eg≈2.43eV). The least of Eg value among all considered clusters about 2.18 ev and it belongs to Be11ScO12. The plot of Eg as a function of atomic number (z) indicates in Figure. 2.
| Molecule | EHOMO | ELUMO | Eg | μ | ?E% | α | β? |
|---|---|---|---|---|---|---|---|
| Be12O12 | -8.64 | -1.04 | 7.60 | 0.00 | 0 | 127.55 | 0 |
| Be11ScO12 | -3.69 | -1.51 | 2.18 | -2.46 | -71.32 | 187.01 | 4953.19 |
| Be11TiO12 | -3.99 | -1.56 | 2.43 | -2.78 | -68.03 | 165.94 | 2757.35 |
| Be11VO12 | -4.64 | -1.88 | 2.76 | -3.50 | -63.68 | 155.83 | 2106.40 |
| Be11CrO12 | -5.17 | -2.27 | 2.90 | -3.72 | -61.84 | 149.31 | 1343.50 |
| Be11MnO12 | -5.43 | -2.17 | 3.26 | -4.07 | -57.11 | 145.03 | 1069.90 |
| Be11FeO12 | -6.28 | -2.15 | 4.13 | -4.22 | -45.66 | 142.70 | 777.53 |
| Be11CoO12 | -7.34 | -3.18 | 4.16 | -5.32 | -45.26 | 139.71 | 348.33 |
| Be11NiO12 | -6.98 | -3.91 | 3.07 | -5.45 | -59.61 | 138.88 | 166.20 |
| Be11CuO12 | -7.84 | -4.54 | 3.30 | -4.77 | -56.58 | 139.33 | 248.36 |
| Be11ZnO12 | -8.13 | -2.30 | 5.83 | -5.22 | -23.29 | 136.23 | 175.34 |
TABLE. 2. The frontier molecular orbital energies EHOMO and ELUMO (eV), energy gap Eg (eV), chemical potential μ (ev), percent of difference energy gap from Be12O12 Δ(E0g-Eg) %, polarizability α (au) and First hyperpolarizability β? (au) values for the considered doped Be12O12 nanocluster.
Figure 2: The changes of energy gap (Eg) as function of atomic number of the doped transition metal atom (Z) for all considered nano clusters Be11XO12
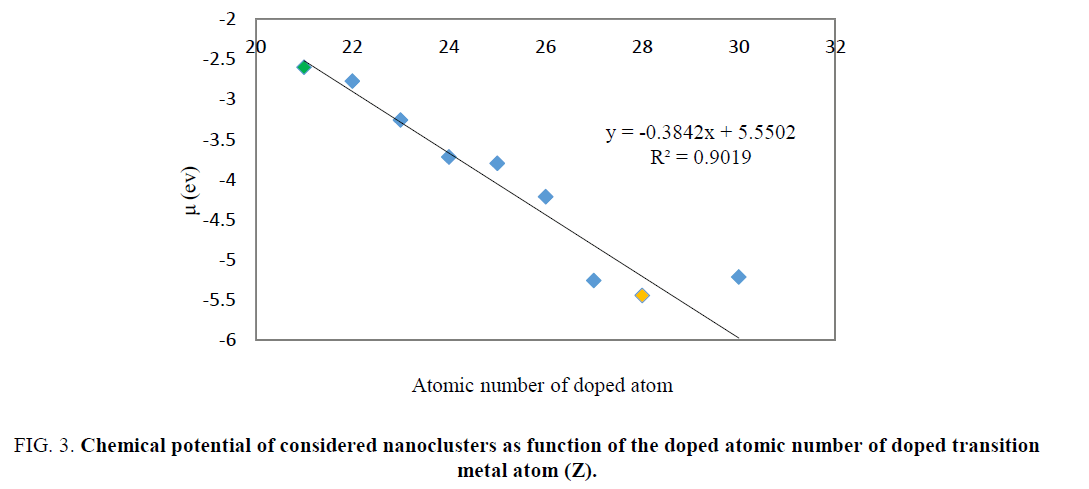
The energy gap values for doped nanocluster Be11XO12 increase with increasing atomic number. The chemical potential of Be11XO12 was calculated and summarized in TABLE 2. The energy gap values for doped nanocluster Be11XO12 increase with increasing atomic number. The chemical potential analysis shows that doping of X atoms in Be12O12 nanocluster leads to the increasing of chemical potential. The maximum chemical potential value occurs in Be11TiO12. In Figure. 3, we can see the reduction of Chemical potential Be12O12 as a function of atomic number.
Figure 3: Chemical potential of considered nanoclusters as function of the doped atomic number of doped transition metal atom (Z).
Optical properties
Polarizability (α) and first hyperpolarizability (β0) for all structures were calculated and listed in TABLE. 2.
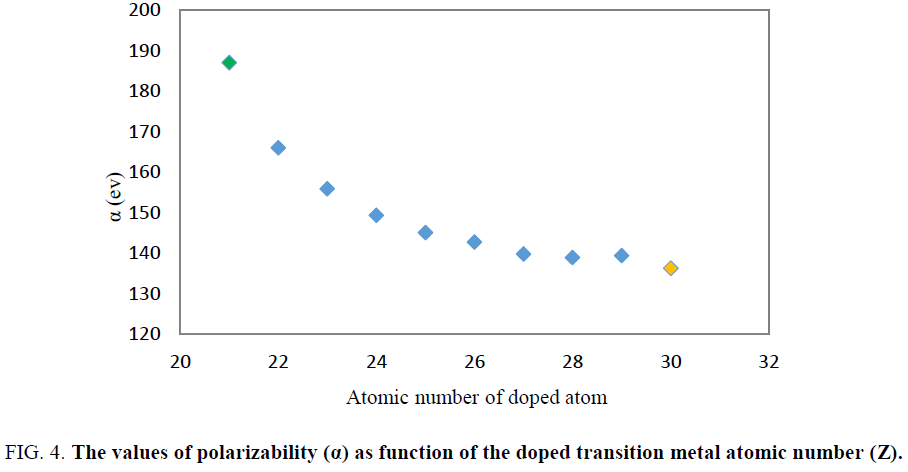
The value of 127.55 and 0 a.u. were obtained for polarizability (α) and first hyperpolarizability (β0) of Be12O12 respectively. The results indicated that doping of transition metals atom in Be12O12 leads to increase the polarizability (α) and first hyperpolarizability (β0) of cluster. Among all of the considered doped nanoclusters by transition metals atom, Be11ScO12 (X=Sc) has the largest first hyperpolarizability (β0≈4953.2 au) and polarizability (α≈187.01 au) values. It was seen that by increasing the atomic number of doped transition metal the polarizability and first hyperpolarizability values was reduced (Figure. 4 and Figure. 5).
Figure 4: The values of polarizability (α) as function of the doped transition metal atomic number (Z).
Figure 5: Logarithmic plot of first hyperpolarizability(β?) as a function of the doped transition metal atomic number (Z) for all considered nanoclustrers.
Similar to previous research, the Sc atom doping had maximum effect on the polarizability and first hyperpolarizability of Be11XO12. Additionally, polarizability and hyperpolarizability decrease when the atomic number of transition metal increases. However larger size of Mg11ScO12 in comparison to Be11ScO12 may explain the larger value of first hyperpolarizability of Mg11ScO12.
TD-DFT calculations
To understand how doping of different transition metals effect on the β0 values of Be12O12, the widely common two-level model is considered as [34-37]:
β0 αΔμ.f/ΔE3 (6)
where ΔE, f0 and Δμ are the transition energy, oscillator strength, and difference in the dipole moments between the ground state and the crucial excited state with the largest oscillator strength. In this model, the third power of the transition energy is reversely proportional to the β0 value; therefore the transition energy is the noteworthy factor in the first hyperpolarizability. The fraction of Δμ.f/ΔE3 in Eq 6, voluntary named as β2. The crucial transition excited state is provided using the time-dependent density functional theory (TD-DFT) calculations at CAM-B3LYP/6-31+G(d) level of theory. The obtained values of ΔE, λ (wavelength of adsorbed light), f0, Δμ and the β2 as well as ln (β0) are presented in TABLE 3.
| System | Ln β (ev) | ?E (ev) | λ (nm) | ?µ ge(a.u) | f | β2 (a.u) |
|---|---|---|---|---|---|---|
| Be11ScO12 | 8.51 | 2.17 | 570.80 | 0.49 | 0.09 | 15.00 |
| Be11TiO12 | 7.92 | 3.37 | 368.40 | 0.40 | 0.05 | 10.15 |
| Be11VO12 | 7.65 | 3.67 | 337.46 | 0.32 | 0.07 | 9.75 |
| Be11CrO12 | 7.20 | 4.17 | 297.39 | 0.24 | 0.13 | 8.61 |
| Be11MnO12 | 6.98 | 4.23 | 292.96 | 0.25 | 0.12 | 7.74 |
| Be11FeO12 | 6.66 | 4.48 | 276.89 | 0.23 | 0.12 | 6.00 |
| Be11CoO12 | 5.85 | 5.56 | 214.60 | 0.29 | 0.08 | 2.67 |
| Be11NiO12 | 5.11 | 6.11 | 202.98 | 0.49 | 0.03 | 1.34 |
| Be11CuO12 | 5.51 | 4.31 | 287.59 | 0.48 | 0.03 | 4.02 |
| Be11ZnO12 | 5.17 | 7.02 | 176.56 | 1.70 | 0.05 | 5.04 |
TABLE. 3. The first hyperpolarizability (β0), the transition energy (ΔE), the difference of dipole moment (Δμ) between the ground state and the crucial excited state, the largest oscillator strength (f) of the considered nanoclusters.
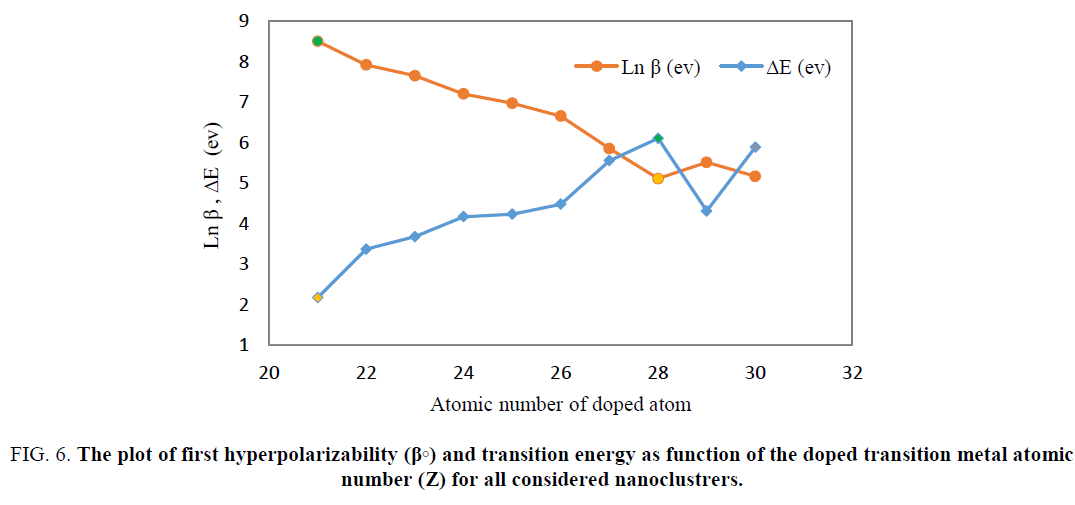
For all doped nano clusters (Be11XO12), calculated excitation energy was compared with the first hyperpolarizibility obtained from TABLE 2 and was show that in the cases which have lower excitation energy, the hyperpolarizability has higher value. In Figure. 6 the simultaneously the hyperpolarizability and excitation energy of transition of doped nanocages were plotted as function of atomic number of used transition metal atoms.
Figure 6: The plot of first hyperpolarizability (β?) and transition energy as function of the doped transition metal atomic number (Z) for all considered nanoclustrers.
As indicated in Eq 6, the first hyperpolarizability of the doped nanoclusters is inversely proportional to the transition energies. The highest first hyperpolarizability and the lowest transition energy were observed in Be11ScO12. Additionally, the lowest first hyperpolarizability was obtained for Be11NiO12 had highest value of transition energy.
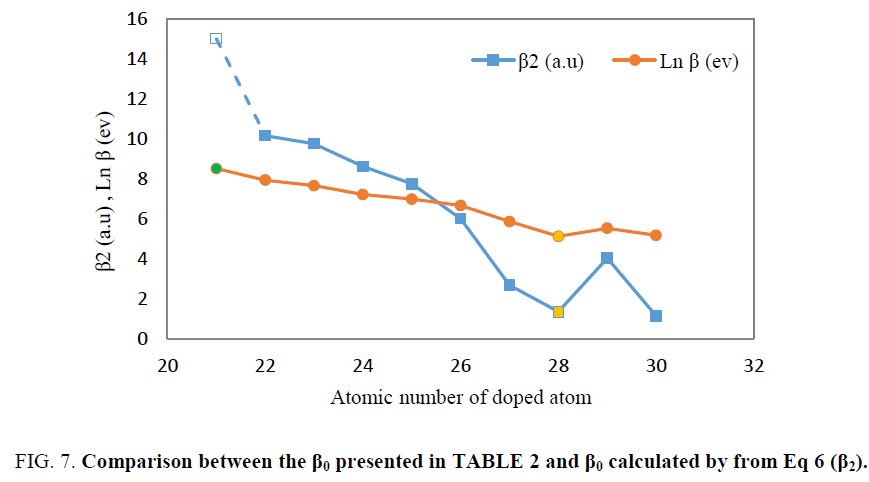
Finally, the first hyperpolarizability presented in TABLE 2, was compared with values of hyperpolarizability calculated by Eq 6. It was seen that the trend of both of them as function of atomic number of transition metals are similar. In Figure. 7, both of the plots of logarithm of first hyperpolarizability calculated from direct ab initio calculation and the β2 obtained from Eq 6 were plotted as function of atomic number of transition metals.
As illustrated in Figure. 7, logarithm of first hyperpolarizabilty calculated by ab initio calculation has same behavior as β0 obtained from Eq 6.
Conclusion
The aim of this study was to evaluate the effect of doping transition metals atom on the structural, electronic, linear and nonlinear optical properties of Be12O12 nanocluster by density functional theory (DFT) methods. The main conclusions of this paper can be summarized as follows:
1. Transition metals atom doping in Be12O12 nanocluster due to reduction of energy gap Be12O12. The maximum decrement belongs to Be11TiO12 (-68.03%) and the minimum decrement belongs to Be11CuO12 (-12.89%).
2. The doping of transition metals atom in Be12O12 leads to enhancement of polarizability (α). The Be11ScO12 has the greatest polarizability (α = 187.01 eV) and Be11ZnO12 has the lowest polarizability (α = 136.23 eV).
3. The first hyperpolarizability values increases with transition metals atom doping. The first hyperpolarizability for considered nanoclusters are change in the order of (Sc) > (Ti) > (V) > (Cr) > (Mn) > (Fe) > (Co) > (Cu) > (Ni) > (Zn).
4. The two-level model proposes that the considerable increment of β0 is mainly due to the ΔE values. Additionally, the TD-DFT calculation indicates that the first hyperpolarizability has similar behavior as β2 and inverse of ΔE3.
5. The doping process of transition metals atom in the Be12O12 nanocluster plays an important role in enhancing the first hyperpolarizability and leads to the NLO response.
References
- Kleinman DA. Nonlinear dielectric polarization in optical media. Phys Rev. 1962;126:1977.
- Pandey V, Mehta N, Tripathi SK, et al. Optical band gap and optical constants in Se85Te15-xPbx thin films. J. Optoelectron. Adv Mater. 2005;7:2641-6.
- Zhong RL, Xu HL, Muhammad S, et al. The stability and nonlinear optical properties: Encapsulation of an excess electron compound LiCN? Li within boron nitride nanotubes. J Mater Chem. 2012;22:2196-202.
- Tu C, Yu G, Yang G, et al. Constructing (super) alkali–boron-heterofullerene dyads: an effective approach to achieve large first hyperpolarizabilities and high stabilities in M3O–BC59 (M= Li, Na and K) and K@ n-BC59 (n= 5 and 6).PhysChemChem Phys. 2014;16:1597-606.
- Zhou F, He JH, Liu Q, et al. Materials chemistry. J Mater Chem. 2014;100: 6850-8.
- Hatua K, Nandi PK. Beryllium-cyclobutadienemultidecker inverse sandwiches: electronic structure and second-hyperpolarizability. J PhysChem A. 2013;117:12581-9.
- Muhammad S, Xu H, Su Z. Capturing a synergistic effect of a conical push and an inward pull in fluoro derivatives of Li@ B10H14 basket: toward a higher vertical ionization potential and nonlinear optical response. J PhysChem A. 2011;115:923-31.
- Marder SR, Gorman CB, Meyers F, etal. A unified description of linear and nonlinear polarization in organic polymethine dyes. Science. 1994;265:632-5.
- Shakerzadeh E. A theoretical study on the influence of carbon and silicon doping on the structural and electronic properties of (BeO)12nanocluster. J InorgOrganometPolym. 2014;24:694-705.
- Shakerzadeh E. A theoretical study on pristine and doped germanium carbide nanoclusters. J MaterSci Mater Electron. 2014;25:4193-9.
- Niu M, Yu G, Yang G, et al. Doping the alkali atom: an effective strategy to improve the electronic and nonlinear optical properties of the inorganic Al12N12nanocage. InorgChem. 2013;53:349-58.
- Iijima S. Helical microtubules of graphitic carbon. Nature. 1991;354:56-8.
- Fabia?ski R, Firlej L, Zahab A, et al. Relationships between crystallinity, oxygen diffusion and electrical conductivity of evaporated C 70 thin films. Solid State Sci. 2002;4:1009-15.
- Ma TB, Hu YZ, Wang H. Growth of ultrathin diamond-like carbon films by C60 cluster assembly: molecular dynamics simulations. DiamRelat Mater. 2009;18:88-94.
- Jalbout AF. Endohedralmetallo (80) fullerene interactions with small polar molecules. Comput Mater Sci. 2009;44:1065-70.
- Lee JH, Lee BS, Au FT, et al. Vibrational and dynamic analysis of C60 and C30 fullerenes using FEM. Comput Mater Sci. 2012;56:131-40.
- Jain A, Kumar V, Kawazoe Y. Ring structures of small ZnO clusters. Comput Mater Sci. 2006;36:258-62.
- Beheshtian J, Bagheri Z, Kamfiroozi M, et al. A comparative study on the B12N12, Al12N12, B12P12 and Al12P12 fullerene-like cages. J Mol Model. 2012;18:2653-8.
- Kakemam J, Peyghan AA. Electronic, energetic, and structural properties of C-and Si-doped Mg12O12 nano-cages. Comput Mater Sci. 2013;79:352-5.
- Hong L, Wang H, Cheng J, et al. Lowest-energy structures of (MgO) n (n= 2–7) clusters from a topological method and first-principles calculations. ComputTheor Chem. 2012;980:62-7.
- Shakerzdeh E, Tahmasebi E, Shamlouei HR. The influence of alkali metals (Li, Na and K) interaction with Be12O12 and Mg12O12nanoclusters on their structural, electronic and nonlinear optical properties: A theoretical study. Synthetic Metals. 2015;204:17-24.
- Tahmasebi E, Shakerzadeh E, Biglari Z. Theoretical assessment of the electro-optical features of the group III nitrides (B12N12, Al12N12 and Ga12N12) and group IV carbides (C24, Si12C12 and Ge12C12) nano-clusters encapsulated with alkali metals (Li, Na and K). Appl Surf Sci. 2016;363:197-208.
- Shamlouei HR, Nouri A, Mohammadi A, et al. Influence of transition metal atoms doping on structural, electronic and nonlinear optical properties of Mg12O12nanoclusters: A DFT study. Physica E Low DimensSystNanostruct. 2016;77:48-53.
- Frisch MJ, Trucks GW, Schlegel HB, et al. Gaussian 09, revision a. 02, Gaussian. Inc., Wallingford, CT. 2009;200.
- Yanai T, Tew DP, Handy NC. A new hybrid exchange–correlation functional uses the Coulomb-attenuating method (CAM-B3LYP). ChemPhysLett. 2004;393(1):51-7.
- Jacquemin D, Perpète EA, Scalmani G, et al. Assessment of the efficiency of long-range corrected functionals for some properties of large compounds. J Chem Phys. 2007;126:144-145.
- Limacher PA, Mikkelsen KV, Lüthi HP. On the accurate calculation of polarizabilities and second hyperpolarizabilities of polyacetylene oligomer chains using the CAM-B3LYP density functional. J Chem Phys. 2009;130:194114.
- Janjua MR, Jamil S, Ahmad T, et al. Quantum chemical perspective of efficient NLO materials based on dipolar trans-tetraammineruthenium (II) complexes with pyridinium and thiocyanate ligands: First theoretical framework. ComputTheor Chem. 2014;1033:6-13.
- O'boyle NM, Tenderholt AL, Langner KM. CCLIB: A library for package?independent computational chemistry algorithms. J Comput Chem. 2008;29:839-45.
- Buckingham AD. Permanent and induced molecular moments and long-range intermolecular forces. AdvChem Phys.1967;12:107-42.
- McLean AD, Yoshimine M. Theory of molecular polarizabilities. J Chem Phys. 1967;47:1927-35.
- Thanthiriwatte KS, De Silva KN. Non-linear optical properties of novel fluorenyl derivatives—ab initio quantum chemical calculations. J MolStructTheochem. 2002;617:169-75.
- Wang JJ, Zhou ZJ, Bai Y, et al.The interaction between super-alkalis (M3O, M = Na, K) and a C20F20 cage forming superalkalielectride salt molecules with excess electrons inside the C20F20 cage: dramatic superalkali effect on the nonlinear optical property. J Mater Chem, 2012;22:9652-7.
- Oudar JL, Chemla DS. Hyperpolarizabilities of the nitroanilines and their relations to the excited state dipole moment. J Chem Phys. 1977;66:2664-8.
- Oudar JD. Optical non-linearities of conjugated molecules. Stilbene derivatives and highly polar aromatic compounds. J Chem Phys. 1977;67:446-57.
- Kanis DR, Ratner MA, Marks TJ. Design and construction of molecular assemblies with large second-order optical nonlinearities. Quantum chemical aspects. Chem Rev. 1994;94:195-242.
- Datta A, Pati SK. Dipolar interactions and hydrogen bonding in supramolecular aggregates: understanding cooperative phenomena for 1st hyperpolarizability. ChemSoc Rev. 2006;35:1305-23.