Original Article

, Volume: 10( 3)

• View PDF
• Download PDF

Tracer Dynamics in Polymer Networks

*Correspondence:

Benmouna F, Faculty of Sciences, University of Tlemcen BP 119, Tlemcen, Algeria 13000, Tel: +213775151175; E-mail: fbenmouna@email.com

Abstract

The dynamics of a trace amount of linear chains in a swollen network are investigated in the presence of excluded volume interaction and long range hydrodynamic back flow effects via Oseen tensor description. The practical interest on tracer diffusion has triggered the development of fluorescence correlation spectroscopy as a direct way to have access to the tracer diffusion coefficient. We present an approach based on slow and fast mode theories to show that the quasi elastic scattering technique provides another, indirect way to reach a wealth of information in addition to the diffusion coefficient. We invoke the blob model as a way to analyze the properties of a trace amount of polymer in a host medium made of free chains and hint to its extension to a cross-linked network. The random phase approximation in the static and dynamic versions is used to obtain the properties of the slow and fast relaxation modes, the former one being reminiscent of tracer dynamics.

Keywords

Tracer diffusion; Cross-linked network; Blob; Excluded volume; Hydrodynamic; Slow mode; Fast mode; First cumulant

Introduction

The conformation and diffusion of single chains in polymer networks has been the subject of interest for decades [1-5]. The reptation model suggested by de Gennes was at the origin of a large number of investigations both from the experimental and theoretical points of view, to discuss the conditions of its validity [6]. It was considered essentially through the scaling behavior of relaxation times and viscosity with respect to the molecular weight. Reptation is reminiscent of high molecular weight polymers and describe slow relaxations over long times. For shorter polymers, chain dynamics can be described by classical models such as Rouse and Zimm depending on the viscosity, and whether long range hydrodynamic backflow effects are present or not. In recent years, a renewed interest on these questions was witnessed, which triggered the development of fluorescence correlation spectroscopy as a powerful tool for investigating tracer diffusion [7-9].

The interest on structure and dynamics of single chains in polymer networks steams from the variety of applications encompassing separation processes drug delivery and chemical synthesis of interpenetrated networks beside other applications. In this work, we present a theoretical formalism dedicated to the study of single chain behavior in a host medium made of a cross-linked network of polymer either of the same monomer species or a distinct one. We consider both dynamic and static properties. In order to better grasp the effects of crosslinks in the host medium, we consider also the case of the network counterpart made of free chains [10-13]. This is the reason why we include in our analysis, the predictions of the celebrated blob model.

The blob model

The reptation model assumes that long chains execute a motion resembling that of reptile, in trying to avoid obstacles put by chains surrounding it. A theory based on scaling laws was proposed by de Gennes generating debates for many years to identify the conditions under which the chain dynamics can be attributed to reptation. This dynamical model does not help understanding static properties while the blob approach is somewhat more general and can be applied to both static and dynamic quantities as we illustrate below.

The case of free chains

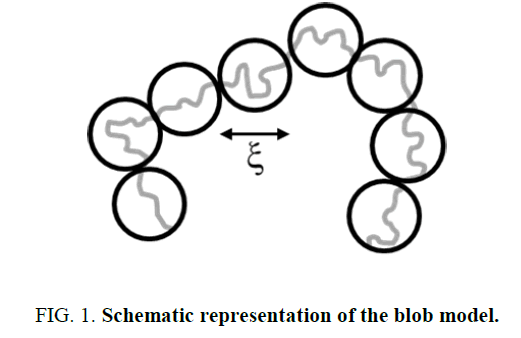
The blob model is often used for a host medium made of free chains, and gives an illustration of it (Figure 1). The labelled chain is represented as a succession of blobs which consist of spheres of diameter ξ coresponding to the mean distance between neighboring chains. The cross over from good to theta solvent behavior takes place at the blob ends.

The case of a labeled chain in a host medium made of free identical unlabeled chains can be treated using the blob model suggested by de Gennes [6]. Beside the solvent quality which is assumed to be good for both A (unlabeled polymer matrix) and B (labeled single chain) species, there are several parameters characterizing the system. First, the blob size which is fixed by the concentration corresponds to the average distance between neighboring A-chains denoted ξ, directly related to the number of monomers N_c. Another important parameter is the B-chain chemical length N_B. In the blob model, a cross over takes place from good to theta solvent behavior at N_B=N_c. This means that if the chemical distance n between two monomers on the B-chain is lower than Nc (i.e. n ≤ N_c), one finds a single chain behavior while for n ≥ Nc, one observes many chain properties and theta solvent behavior. In other words, a screening of excluded volume interactions takes place beyond Nc, and formally, one writes [14].

(1)

(2)

N_c and ξ depend on the polymer concentration C according to the scaling laws (for v =3/5), hence, the blob size decreases as the concentration increases. One can use this formulation to calculate the properties of labeled chains as a function of C, such as the radius of gyration R_g defined by,

(3)

Since depends on only, we can transform the double sum into a single one, and for large N, we can go to the continuum limit replacing discrete sums by integrals to get,

(4)

Substituting from eqns. (1) and (2), recalling yields the ratio in terms of u=Nc/N only,

(5)

Note that the form factor P(q) is immediately deduced from R_g since,

(6)

Where, q is the amplitude of the scattering wave vector. Another illustration of the blob model concerns the diffusion coefficient D, which can be calculated in the presence of hydrodynamic interaction, from the angular pre averaged Oseen tensor [15].

(7)

From the definition of D, and ignoring the Rouse term, one writes:

(8)

With similar manipulations as in the case of R_g, we get,

(9)

Where the function δ (u) is given by,

(10)

The hydrodynamic radius R_h can be deduced from the diffusion coefficient and the known relationship,

(11)

Let us point out that, in the Rouse limit, the dynamics are governed by local frictional forces only, and the diffusion coefficient becomes:

(12)

The monomer friction coefficient z is related to the viscosity h by Stock’s law z = 6phl” Represents the monomer friction coefficient 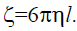. The question to be asked is whether this blob model can be extended to the case where the host medium is a cross-linked network noting that the blob size depends on the polymer concentration, while for a cross-linked network, it is fixed by the degree of cross-linking.

Effects of cross-linking

Here, we show that by considering the second derivative of the free energy for a cross-linked network in solution (i.e. the spinodal equation), one finds that the result has the form known for a linear polymer/solvent binary solution, with a renormalized degree of polymerization N depending on the cross-linking density. According to the Flory Rehner theory of rubber elasticity [16] the free energy of a network a swollen by solvent S is,

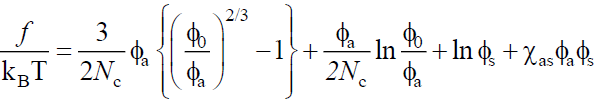(13)

Where, χ_as is the polymer A/solvent interaction parameter. The second derivative with respect to Φ_a is,

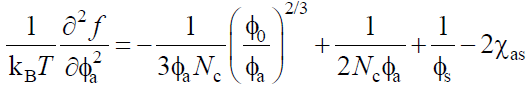(14)

We recall that the corresponding quantity for a linear polymer/solvent system is,

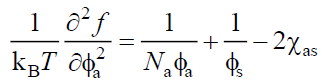(15)

It means that, by renormalizing the degree of polymerization N_a in the following way:

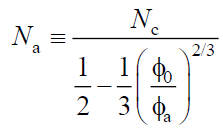(16)

One can go from the cross-linked network to the free chain system. This argument is however not sufficient, and does not allow us to validate the extension of the blob model to a cross-linked host medium. Since this extension requires a more refined analysis, we postpone its discussion to a future work and turn to tracer dynamics.

Dynamics of linear chains in cross-linked networks

Polymer chains swell in good solvents and shrink under poor solvent conditions. Such responses are mainly due to excluded volume interactions and depend on whether the solvent temperature is above (swelling) or below (deswelling) the characteristic theta value. Similar responses are found for strands between consecutive crosslinks in networks or gels.

Swelling and deswelling processes play the key role in many applications such as drug delivery and targeting with molecules having active principles and specific functionalities. Such smart responses can be used to liberate molecules from a contracted network by solvent uptake, or sequestrate them by rejecting solvent. The partition of molecules in and outside the network at equilibrium depends on the chemical potential. Any discontinuity in this potential induces transfer of molecules across the network’s boundary via dynamical processes. If the amount of linear chains is low, their diffusion in the network becomes reminiscent of tracer diffusion. Therefore, in order to study the dynamics of a trace amount of polymer (i.e. single chain) in a cross-linked network, we introduce the random phase approximation (RPA) and start with static properties representing a prerequisite to dynamics.

Static properties

In its static form, the RPA gives the matrix of partial structure factors in Fourier space S s in terms of the scattering wave vector q, its counterpart S₀ (q) for non-interacting systems and the matrix of excluded volume parameters v,

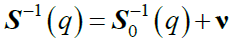(17)

Resolution of this equation for the ternary system network A/linear polymer B/solvent S yields the explicit forms of partial structure factors S_ij (q) as follows:

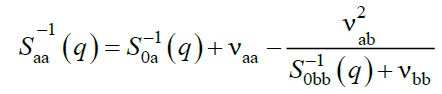(18)

S_bb(q) can be obtained from this expression by interchanging indices a and b, and S_ab (q) is,

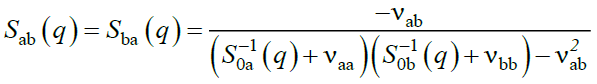(19)

The excluded volume parameters v_ij depend on solvent volume fraction Φ_s and interaction parameter χ_ij as:

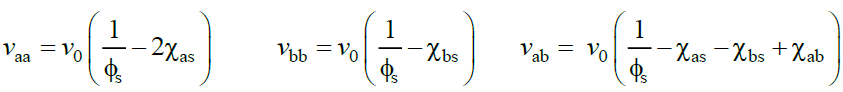(20)

Where, v₀ is a standard unit volume. To proceed further, one needs the bare structure factor S_0i (q), which for the network A, takes the classical Ornstein Zernike form (17),

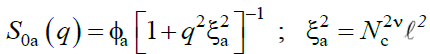(21)

Φ_a being the network volume fraction. For the trace amount of linear chains B, we have,

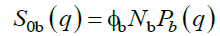(22)

Φ_b being the volume fraction of B, N_b its degree of polymerization, and P_b(q) its form factor expressed in terms of the radius of gyration R_gb as:

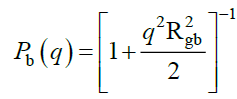(23)

Once we have characterized the static properties, we can turn to dynamics starting with the first cumulant Ω (q).

The first cumulant

The first cumulant describes the dynamical relaxations at relatively short times before buildup of long time memory effects. This frequency is often found to characterize the major aspects of the dynamical behavior in the relevant space and time domains. It is easily accessible to modeling in terms of the system’s parameters, allowing a direct confrontation with experiments. : For a multicomponent system, the matrix W(q) is proportional to the ratio of mobility and structure matrices M(q) and S(q), respectively, Ω (q) is proportional to the ratio of mobility.

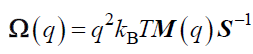(24)

Solving this equation for the ternary mixture A/B/S yields,

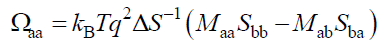(25)

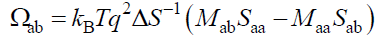(26)

Where 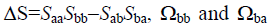can be inferred from eqns. (25) and (26), respectively, simply upon interchange of indices a and b, noting that, in general, 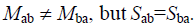The mobility M_ij depends on the specific hydrodynamic model chosen to describe frictional forces and viscous backflow effects. We discuss these differences below by examining explicitly the effects of long range hydrodynamic interactions. We recall that Rouse and Zimm hydrodynamic models are valid at relatively short times, while reptation intervenes only at very long times and necessitates the inclusion of memory effects which is beyond the scope of the present work.

In the presence of hydrodynamic interaction, Ωij can be expressed as sums of two parts, one dealing with short range frictional forces of the Rouse type, and the other, reminiscent of the long range hydrodynamic backflow effects, described by the Oseen tensor T_ij,

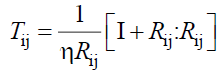(27)

R_ij being the vector distance between i and j monomers. In the following results, we use the superscript R to designate Rouse dynamics and introduce the integrals J_ij representing the long range hydrodynamic interaction,

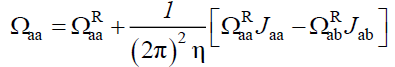(28)

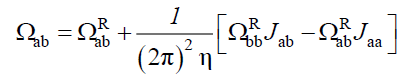(29)

Ω_bb is inferred from Ω_aa while Ω_ba from Ω_ab by a proper interchange of indices a and b. The Rouse terms in these equations are fixed by the static structure factors,

(30)

While the integral J_ij may be written as:

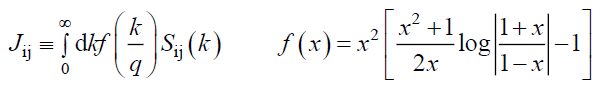(31)

We shall assume, without loss of generality, that the friction coefficients are equal za = zb = z”, that the friction coefficients ζ_a and ζ_b are equal and related to the viscosity by Stock’s law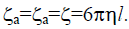

Fast and slow modes

Within linear response theory, the generalized Langevin equation for Σ (q,t), the matrix of dynamical scattering functions is given by,

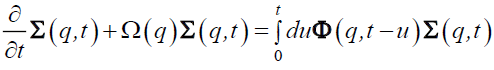(32)

The RHS expresses the effects of memory at long times and will be disregarded here, which means that the solution has a simple exponential form:

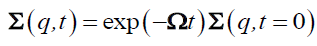(33)

Solving this equation for the ternary mixture A/B/S, yields the four elements of the dynamic scattering matrix Σ_aa (q, t), Σ_bb (q, t), Σ_ab (q, t) and Σ_ba (q, t). The first one Σ_aa (q, t) characterizes the host medium, it describes how host chains modify the network relaxations inhibiting its swelling behavior. Motion of the trace amount of polymer B can be extracted from the four Σ’s and in particular from Σ_bb (q, t). Resolution of eqn. (33) yields:

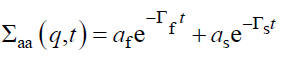(34)

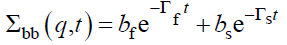(35)

The subscripts f and s refer to fast and slow modes, respectively; Γ’s are the Eigen values of Ω (q), while a’s and b’s are the mode amplitudes and satisfy the conditions 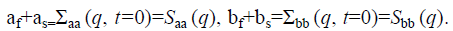The two Eigen values of the first cumulant matrix Ω are,

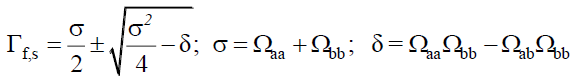(36)

One can proceed further by calculating the frequencies and amplitudes of the modes under specified conditions of the system given its parameter values. In the case of a trace amount of the probe B, the volume fraction Φ_B must be chosen small meaning that the ratio Φ_b/(Φ_a + Φ_b) must be much less than 1. In this case, one can deduce useful information about the modes and in particular the tracer diffusion coefficient. Recall that the fast mode is essentially influenced by the network dynamics reflecting the total polymer concentration fluctuations, while the slow mode is reminiscent of the probe diffusion throughout the obstacles set by the network. It is this one which gives the tracer diffusion when the volume fraction Φ_B is small. We will content ourselves with few numerical applications, hoping to report a more detailed analysis in the near future.

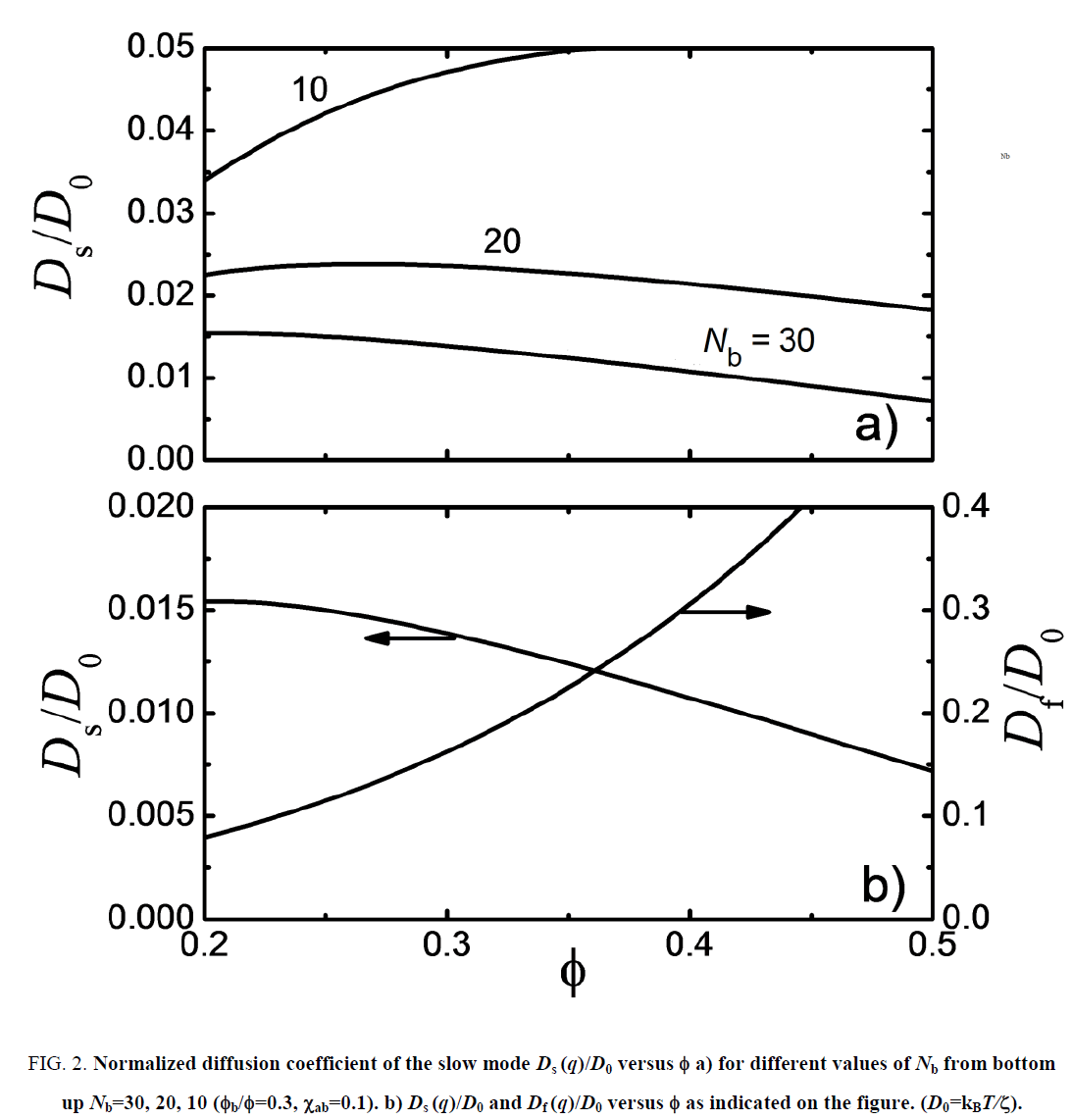
In Figure 2a, we represent the normalized diffusion coefficient for the slow mode as a function of the polymer volume fraction. The curves show a slowing down of the diffusion when N_b increases above N_C. For short chains and N_b<N_C, this tendency is reversed and the slow mode speeds up as the polymer concentration increases. It is interesting to note that the fast mode exhibits the reverse trend since the corresponding diffusion coefficient goes up with a higher concentration of the medium as shown in Figure 2b.

On the other hand, when the incompatibility of the two polymer species increases with a higher value of χ_ab, the slow process slows down further following enhanced fluctuations, especially for Φ sufficiently high (Figure 3a). This behavior is reminiscent of the critical slowing down known for interdiffusive relaxation. However, the fast mode speeds up in response to a higher χ_AB interaction as one can see from Figure 3b shows opposite trends for fast and slow diffusion as a function of polymer volume fraction f” As pointed out earlier, we content ourselves with those applications of the proposed model leaving a more detailed quantitative analysis for the near future.

Result, Discussion and Conclusion

The dynamics of single chains in a polymer matrix has received a renewed interest under the terminology of tracer diffusion after the emergence of new applications in Nano sciences and nanotechnologies. Clearly, the knowledge of the properties of a single chain in a polymer medium made either of identical unlabeled chains, slightly different, or entirely distinct matrices is of primary importance for understanding the properties of guest/host systems in general. For a single labeled chain in a sea of identical unlabeled chains, the blob model describes the behavior from small scales (i.e within the blob) to larger ones (for monomers far apart located at a distance higher than the blob size). The blob marks the transition from single to many chains behavior and its size decreases with increasing concentration. This model is reasonable for semi dilute and concentrated solutions but it was applied so far only for labeled chains, in a matrix of identical unlabeled free chains. In the present work, we suggest extending it to tracer diffusion in a cross-linked network. Here, one deals with two distinct species even in the case where monomer units are similar. The dynamics of the linear chain and the cross-linked network correspond to different mechanisms and may fall on different time scales. This is why the two-mode approach was proposed based on the random phase approximation.

The general theory based on this approximation is given in matrix form including static and dynamic considerations. In the case of three component systems, cross-linked network A/linear chain B/solvent S, one finds a combination of fast and slow processes which we identified according to their frequencies and amplitudes. We presumed that tracer dynamics can be extracted from the slow process provided that parameter values are chosen adequately. The proper choice must be made for contrast factors (i.e. which signal to be probed), degree of crosslinking, the size of the linear chain compared to that of the network strand (i.e. confinement ratio Rg (chain)/ξ (network)), the interaction parameters (i.e. excluded volumes) and the amount of linear chains (i.e. volume fraction). In the Rouse limit, the dynamics depend essentially on static structure factors and the monomer friction coefficient. If long range hydrodynamic interactions and backflow effects are present, then a model developed by Zimm based on the Oseen tensor can be adopted. Substantial changes from the Rouse limit are found but need to be evaluated numerically with a reasonable choice of the system parameters. This choice is often dictated by the experimental conditions and the measured quantities and we hope to report in the future, a detailed numerical analysis of the predictions of the formalism, along with a confrontation with experiments.

References

1. Doi M, Edwards SF. The theory of polymer dynamics. Oxford University Press, 1988:73.
2. De Gennes PG. Dynamics of entangled polymer solutions. I. The Rouse model. Macromolecules. 1976;9(4):587-93.
3. Tong J, Anderson JL. Partitioning and diffusion of proteins and linear polymers in polyacrylamide gels. Biophysical Journal. 1996;70(3):1505-13.
4. Bansil R, Pajevic S, Konak C. Diffusion of polystyrene in gels. Macromolecules. 1990;23(13):3380-82.
5. Seiffert S, Oppermann W. Diffusion of linear macromolecules and spherical particles in semi dilute polymer solutions and polymer networks. Polymer. 2008;49(19): 4115-26.
6. PG de Gennes. Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, NY; 1979.
7. Zettl U, Ballauff M, Harnau L. A fluorescence correlation spectroscopy study of macromolecular tracer diffusion in polymer solutions. J Phys Condens Matter. 2010;22(49):494111.
8. Kamerlin N, Elvingson C. Tracer diffusion in a polymer gel: Simulations of static and dynamic 3D networks using spherical boundary conditions. J Phys: Condens Matter. 2016;28(47):475101.
9. Blanco PM, Via M, Garcés JL, et al. Brownian dynamics computational model of protein diffusion in crowded media with dextran macromolecules as obstacles. Entropy. 2017;19(3):105.
10. Ain Sebaa-Chirani N, Dembahri Z, Tokarski C, et al. Newly designed polyacrylamide/dextan gels for electrophoresis proteins separation: Synthesis and characterization. Polym Int. 2011;60(7):1024-9.
11. Benmouna F, Bouabdellah-Dembahri Z, Benmouna M. Polymerization-induced phase separation: Phase behavior developments and hydrodynamic interaction. J Macromol Sci Phys. 2013;52(7):998-1008.
12. Benmouna M, Benmouna F. Dynamical relaxations of cross linked networks in polymer solutions. ChemXpress. 2016;9(6):112.
13. Benmouna M, Benmouna F. Dynamics of linear chains in polymer networks as a model for drug delivery systems: Preliminary results. ChemXpress. 2017;10(2):1-4.
14. Akcasu AZ, Benmouna M. Concentration effects on the dynamic structure factor in polymer solutions. Macromolecules. 1978;11(6):1193-8.
15. Benmouna M, Akcasu AZ. The effect of preaveraging the Oseen tensor on the characteristic frequency in good solvents. Macromolecules. 1980;13(2):409-14.
16. Flory PJ, Rehner J. Statistical mechanics of cross-linked polymer networks. II. Swelling. J Chem Phys. 1943;11(11):521-6.
17. Benmouna F, Zemmour S, Benmouna M. Ionic networks in polymer solutions: Structural properties and phase behavior. Curr Phys Chem. 2016;6(2):130-6.