Original Article
, Volume: 15( 4)Quantitative Structure-Activity Relationship (QSAR) Studies of Some Glutamine Analogues for Possible Anticancer Activity
- *Correspondence:
- Elidrissi B Molecular Chemistry and Natural Substances Laboratory, Faculty of Science, University Moulay Ismail, Meknes, Morocco
Tel: +212-607662438; E-mail: elidrissi.info@gmail.com
Received Date: August 08, 2017 Accepted Date: September 08, 2017 Published Date: September 12, 2017
Citation: Elidrissi B, Ousaa A, Ajana MA, et al. Quantitative Structure-Activity Relationship (QSAR) Studies of Some Glutamine Analogues for Possible Anticancer Activity. Int J Chem Sci. 2017;15(4):192
Abstract
A quantitative structure-property relationship (QSPR) study was performed to predict anticancer activity in tumor cells of thirty-six 5-N-substituted-2-(substituted benzenesulphonyl) glutamines compounds using the electronic and topologic descriptors computed respectively, with ACD/Chem Sketch and Gaussian 03W programs. The structures of all 36 compounds were optimized using the hybrid density functional theory (DFT) at the B3LYP/6-31G (d) level of theory. In both approaches, 30 compounds were assigned as the training set and the rest as the test set. These compounds were analyzed by the principal components analysis (PCA) method, a descendant multiple linear regression (MLR), multiple nonlinear regression (MNLR) analyses and an artificial neural network (ANN). The robustness of the obtained models was assessed by leave-many-out cross-validation, and external validation through test set. This study shows that the ANN has served marginally better to predict antitumor activity when compared with the results given by predictions made with MLR and MNLR.
Keywords
DFT; QSAR; Tumor cells; Artificial neural network; Cross validation
Introduction
Cancer remains one of the causes of death in the world and as a result there is a pressing need for the development of novel and effective treatments. Despite major breakthroughs in many areas of modern medicine over the past 100 years, the successful treatment of cancer remains a significant challenge at the start of the 21st century. It is very difficult to know and detect novel agents that selectively kill tumor cells or inhibit their proliferation without being toxic [1]. The cancer has been described as nitrogen trap. [2] Glutamine (GLN), a non-essential amino acid, plays a key role in tumor cell growth by supplying its amide nitrogen atoms in the biosyntheses of other amino acids, purine, pyrimidine bases, amino sugars and Coenzymes [3], via a family comprised of 16 amido transferases [4] with diversified mechanisms. So, different structural of glutamines were synthesized and may supposedly show antitumor activities by GLN [5].
In this study, we have modeled the antitumor activity (inhibition of tumor (IT)) of 36 new 5-N-substituted-2-(substituted benzenesulphonyl) glutamines with different substitutions (Table 1), using several statistical tools, principal components analysis (PCA), multiple linear regression (MLR), multiple nonlinear regression (MNLR) and artificial neural network (ANN) calculations [6,7]. The quantitative structure-activity relationship (QSAR) method focuses on the motto that the activities of chemical compounds are determined by their molecular structures. [8] Thus, based on accurate experimental data of only some of the chemicals in one group, the biological activity of chemicals in the whole group can be predicted using the suitable models, including compounds that have not yet been experimentally synthesized [9-13].
The objectives of this work are to develop predictive QSAR models and to identify the chemical structural features important among of our studied molecules for the antitumor cells activity. Thus, a number of quantum chemical methods and calculations have been performed in order to study the molecular structure and antitumor activity [14].
In the present work, to find the quantitative relationship between molecular structure and antitumor activity for the data taken by Srikanth et al. [14], we used the multiple linear regression (MLR), multiple nonlinear regression (MNLR) and artificial neural network (ANN) [15]. We calculated the electronic descriptors by the Gaussian 03 to generate QSAR sets. Then, MLR was utilized to select the structural features of the molecules relevant to the antitumor activity and to construct the linear model, this last model was used to select descriptors as inputs, and ANN was constructed the nonlinear model. Both models were validated by an internal validation method including cross-validation to characterize robustness and an external validation to estimate the predictive power of the models. Final, the ultimate objective was to establish reliable QSAR models to inhibition of tumor weight prediction of 5-N-substituted-2-(substituted benzenesulphonyl) glutamines.
Material and Methods
Experimental data
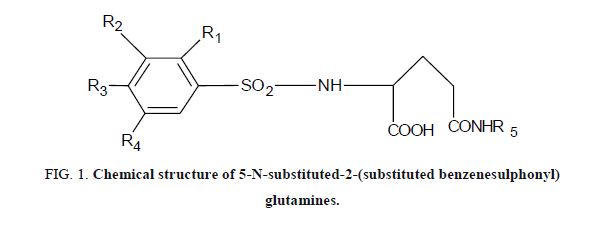
The experimental values of antitumor activities of 36 new 5-N-substituted-2-(substituted benzenesulphonyl) glutamines were taken from the literature [15]. For the tumor growth inhibition, antitumor activity was assessed on the basis of the percentage inhibition of tumor (%IT). The biological activity (IT) data was calibrated to their logarithmic values (log IT). The compounds and their corresponding biological activity Log (IT) values are shown in Figure 1 and Table 1.
Calculation of molecular descriptors
DFT (density functional theory) methods were used in this study. These methods have become very popular in recent years because they can reach similar precision to other methods in less time and less cost from the computational point of view. In agreement with the DFT results, energy of the fundamental state of a polyelectronic system can be expressed through the total electronic density, and in fact, the use of electronic density instead of wave function for calculating the energy constitutes the fundamental base of DFT [16,17] using the B3LYP functional [18] and a 6-31G (d) basis set. The B3LYP, a version of DFT method, uses Becke’s three-parameter functional (B3) and includes a mixture of HF with DFT exchange terms associated with the gradient corrected correlation functional of Lee, Yang and Parr (LYP). The geometry of all species under investigation was determined by optimizing all geometrical variables without any symmetry constraints.
The molecular properties which were calculated: Highest occupied molecular orbital energy EHOMO(eV), lowest unoccupied molecular orbital energy ELUMO (eV), dipole moment μ(Debye), total energy ET (eV), activation energy Ea (eV), absolute electronegativity χ (eV) and the total negative charges of the molecule TNC [19-22].
χ was determined by the following equations: 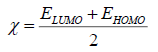 (1)
(1)
On the other hand, ACD/ChemSketch and Chem 3D programs [23] are employed to calculate the topological descriptors which are: Molecular Weight MW(cm3), Density D (g/cm3), Partition Coefficient LogP, Bend Energy Eb(Kcal/mol), Electronic Energy Ee(Kcal/mol), Steric Energy Es(Kcal/mol), Shape Attribute ChA, Shape Coefficient ShC, Mulliken Charges ChM.
Statistical analysis
Principal components analysis (PCA): The compounds of 5-N-substituted-2-(substituted benzenesulphonyl) glutamines (1 to 36) were studied by statistical methods based on the principal component analysis (PCA) [22] using the software XLSTAT 2015. This is an essentially a descriptive statistical method which aims to present, in graphic form, the maximum information’s contained in the data Table 1.
| Compound | R1 | R2 | R3 | R4 | R5 | % Inhibition of tumor weight (IT) | Log (IT) |
|---|---|---|---|---|---|---|---|
| 1 | H | H | H | H | i-Butyl | 52.73 | 1.722 |
| 2 | H | H | CH3 | H | i-Propyl | 50.00 | 1.699 |
| 3 | H | H | CH3 | H | i-Butyl | 25.00 | 1.398 |
| 4 | CH3 | H | H | NO2 | H | 37.5 | 1.574 |
| 5 | CH3 | H | H | NO2 | CH3 | 68.75 | 1.837 |
| 6* | CH3 | H | H | NO2 | C2H5 | 25.00 | 1.398 |
| 7 | CH3 | H | H | NO2 | n-C3H7 | 50.00 | 1.699 |
| 8 | CH3 | H | H | NO2 | n-C4H9 | 62.50 | 1.796 |
| 9* | CH3 | H | H | NO2 | i-Propyl | 62.50 | 1.796 |
| 10 | CH3 | H | H | NO2 | i-Butyl | 12.00 | 1.079 |
| 11 | CH3 | H | H | NO2 | C6H11 | 33.00 | 1.519 |
| 12 | CH3 | H | H | NO2 | C6H5 | 33.00 | 1.519 |
| 13 | CH3 | H | H | NO2 | C6H5CH2 | 60.17 | 1.779 |
| 14 | CH3 | H | H | NO2 | n-C5H11 | 60.83 | 1.784 |
| 15 | CH3 | H | H | NO2 | n-C6H13 | 67.37 | 1.828 |
| 16* | H | NO2 | CH3 | H | H | 49.53 | 1.695 |
| 17 | H | NO2 | CH3 | H | CH3 | 40.86 | 1.611 |
| 18 | H | NO2 | CH3 | H | C2H5 | 27.05 | 1.432 |
| 19 | H | NO2 | CH3 | H | n-C3H7 | 26.95 | 1.431 |
| 20 | H | NO2 | CH3 | H | n-C4H9 | 41.37 | 1.617 |
| 21 | H | NO2 | CH3 | H | n-C5H11 | 24.88 | 1.396 |
| 22 | H | NO2 | CH3 | H | n-C6H13 | 59.45 | 1.774 |
| 23 | H | NO2 | CH3 | H | i-Propyl | 37.64 | 1.576 |
| 24* | H | NO2 | CH3 | H | i-Butyl | 45.95 | 1.662 |
| 25 | H | NO2 | CH3 | H | C6H11 | 35.33 | 1.548 |
| 26 | H | NO2 | CH3 | H | C6H5CH2 | 22.35 | 1.349 |
| 27* | H | NO2 | CH3 | H | C6H5 | 59.60 | 1.775 |
| 28 | H | H | C2H5 | H | CH3 | 90.45 | 1.956 |
| 29 | H | H | C2H5 | H | C2H5 | 38.46 | 1.585 |
| 30 | H | H | C2H5 | H | n-C3H7 | 65.64 | 1.817 |
| 31 | H | H | C2H5 | H | n-C4H9 | 55.64 | 1.745 |
| 32 | H | H | C2H5 | H | n-C5H11 | 56.36 | 1.751 |
| 33 | H | H | C2H5 | H | n-C6H13 | 65.37 | 1.815 |
| 34 | H | H | C2H5 | H | -CH(CH3)2 | 41.53 | 1.618 |
| 35* | H | H | C2H5 | H | C6H5CH5 | 37.50 | 1.574 |
| 36 | H | H | C2H5 | H | C6H5 | 70.76 | 1.850 |
*Test set
Table 1. Experimental antitumor activity of 5-N-substituted-2-(substituted benzenesulphonyl) glutamines values the 36 molecules.
PCA is a statistical technique useful for summarizing all the information’s encoded in the structures of compounds. It is also very helpful for understanding the distribution of the compounds.
Multiple linear regressions (MLR): The multiple linear regression statistic technique was used to study the relation between one dependent variable and several independent variables. It is a mathematic technique that minimizes differences between actual and predicted values. The qualities of the statistics of the MLR equation were judged by parameters such as the R value (coefficient of correlation), the F value (Fischer statistics) and the RMSE value (Root Mean Squared Error).
The multiple linear regression model (MLR) [24] was generated using the software XLSTAT 2015, to predict the antitumor activity (IT). It has served also to select the descriptors used as the input parameters in the multiple nonlinear regression (MNLR) and artificial neural network (ANN).
Artificial neural networks (ANNs)
Nonlinear models were then developed by submitting the selected descriptors from MLR to a three-layer, fully connected, feedforward ANN. The number of input neurons was equal to that of the descriptors in the linear model. The number of hidden neurons was optimized by a trial and error procedure on the training process. One output neuron was used to represent the experimental % inhibition of tumor weight log (IT). To avoid overtraining, one tenth of the data from the training set was randomly selected as a separate validation set to monitor the training process that is during the training of the network the performance was monitored by predicting the values for the systems in the validation set. When the results for the validation set ceased to improve, the training was stopped [25].
Model evaluation and validation
In order to check the reliability and the stability of QSAR model elaborated by MLR, MNLR and ANN methods, both the internal and external validations were conducted. The goodness of the fitting was firstly characterized by the coefficient of determination (R2) between calculated and experimental values for the molecules of the training set. The formula is given by equation:
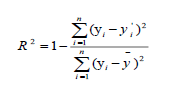 (2)
(2)
Where 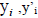 and
and 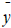 are the observed, calculated and mean values of the activity, respectively.
are the observed, calculated and mean values of the activity, respectively.
Cross-validation is one of the most popular methods of estimating the robustness of a model. Based on this technique, a number of modified data sets are created by deleting in each case one or a small group of molecules, these procedures are named respectively “leave-one-out” and “leave-some-out” [26-28]. In this work, the internal predictive capability of the model was evaluated by the leave-many-out cross-validation 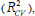 following the mathematic form:
following the mathematic form:
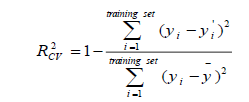 (3)
(3)
The reliability and robustness of the models were further validated by using the external test set composed of data not used to develop the prediction models. The external 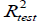 for the test set is determined with the following equation:
for the test set is determined with the following equation:
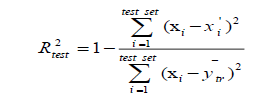 (4)
(4)
where 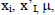 and
and 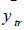 are the observed value, the calculated value in the test set and the mean value of the activity in the training set, respectively.
are the observed value, the calculated value in the test set and the mean value of the activity in the training set, respectively.
QSAR model is successful if it satisfies the following criteria: 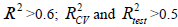
To further refine the predictive ability of the developed QSAR models, another group of metrics was used: the rm 2 metrics. They determine the proximity between the observed and predicted activities, was introduced by Roy and Ojha [27,28]. They are calculated based on the correlation between the observed and predicted response data. Presently two different indicators are calculated for both the training (internal validation) and the test (external validation) sets :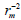 and
and 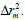 For an acceptable QSAR model
For an acceptable QSAR model 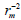 should be>0.5, and
should be>0.5, and 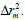 should be<0.2.
should be<0.2.
Y-Randomization test
The models were also evaluated against chance correlation by Y-randomization [29-31]. Property values were randomized within the training set by many iterations. From each new randomized data set, a new model QSAR was computed again, with performances expected to have lower Q2 and R2 values than those the original models. Finally, the average values of the Q2 and R2 were calculated to check that the original model was strongly more performant than the randomized ones (Table 2).
| Log (IT) | MW | D | LogP | Eb | ChM | Es | Ee | ShA | ShC | Et | EHOMO | ELUMO | m | χ | TNC | Ea |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.722 | 342.41 | 1.253 | 0.733 | 13.343 | 0.131 | 118.836 | -31761 | 21.043 | 1.00 | -39990.72 | -6.621 | -3.195 | 7.688 | -4.908 | -9.910 | 2.763 |
| 1.699 | 342.41 | 1.253 | 1.003 | 13.352 | 0.133 | 81.472 | -31303 | 21.043 | 0.85 | -39990.88 | -6.637 | -3.305 | 8.023 | -4.971 | -9.805 | 2.205 |
| 1.398 | 356.44 | 1.231 | 1.221 | 13.547 | 0.132 | 89.597 | -55577 | 22.041 | 0.85 | -41061.16 | -6.553 | -2.441 | 6.856 | -4.497 | -10.526 | 4.327 |
| 1.574 | 345.33 | 1.501 | -0.597 | 13.445 | 0.151 | 124.324 | -31824 | 21.043 | 0.83 | -42347.69 | -6.594 | -3.292 | 7.613 | -4.943 | -9.125 | 4.038 |
| 1.837 | 359.35 | 1.428 | -0.361 | 13.446 | 0.148 | 237.583 | -33793 | 22.041 | 1.00 | -43418.03 | -6.574 | -3.214 | 7.885 | -4.894 | -9.418 | 3.641 |
| 1.398 | 373.38 | 1.392 | -0.023 | 13.446 | 0.132 | 240.852 | -35745 | 23.040 | 0.87 | -43418.03 | -6.574 | -3.214 | 7.885 | -4.894 | -9.418 | 3.632 |
| 1.699 | 387.41 | 1.361 | 0.463 | 13.446 | 0.125 | 243.938 | -37609 | 24.038 | 1.00 | -45559.13 | -6.561 | -3.153 | 8.162 | -4.857 | -10.342 | 3.627 |
| 1.796 | 401.43 | 1.333 | 0.880 | 13.446 | 0.125 | 246.975 | -39468 | 25.037 | 0.85 | -46629.64 | -6.557 | -3.137 | 8.215 | -4.847 | -10.790 | 3.620 |
| 1.796 | 387.41 | 1.359 | 0.295 | 13.727 | 0.135 | 237.493 | -38022 | 24.038 | 0.85 | -45559.20 | -6.535 | -2.853 | 8.055 | -4.694 | -10.375 | 3.138 |
| 1.079 | 401.43 | 1.332 | 0.513 | 13.717 | 0.134 | 243.411 | -40586 | 25.037 | 0.85 | -46629.58 | -6.522 | -2.685 | 8.206 | -4.603 | -10.989 | 4.237 |
| 1.519 | 427.47 | 1.390 | 1.187 | 13.924 | 0.128 | 242.563 | -43662 | 27.034 | 0.85 | -48738.06 | -6.528 | -2.720 | 7.399 | -4.624 | -11.186 | 4.086 |
| 1.519 | 421.42 | 1.452 | 1.302 | 13.445 | 0.199 | 249.208 | -41243 | 27.034 | 0.87 | -48639.08 | -6.425 | -3.630 | 7.482 | -5.027 | -10.095 | 2.779 |
| 1.779 | 435.45 | 1.394 | 1.372 | 13.446 | 0.198 | 241.799 | -44337 | 28.033 | 1.00 | -49709.56 | -6.521 | -2.985 | 7.825 | -4.753 | -9.735 | 2.235 |
| 1.784 | 415.46 | 1.307 | 1.298 | 13.687 | 0.127 | 244.960 | -41310 | 26.035 | 1.00 | -47700.16 | -6.522 | -2.873 | 8.439 | -4.697 | -11.076 | 4.063 |
| 1.828 | 429.49 | 1.285 | 1.715 | 13.884 | 0.118 | 242.747 | -43102 | 27.034 | 0.88 | -48770.67 | -6.521 | -2.872 | 8.430 | -4.697 | -11.687 | 4.056 |
| 1.695 | 345.33 | 1.501 | -0.597 | 13.445 | 0.148 | 108.939 | -31556 | 21.043 | 0.83 | -42347.62 | -6.871 | -2.875 | 8.074 | -4.873 | -9.111 | 4.025 |
| 1.611 | 359.35 | 1.428 | -0.361 | 13.446 | 0.119 | 112.573 | -33511 | 22.041 | 1.00 | -43418.07 | -6.842 | -2.905 | 7.832 | -4.873 | -9.390 | 3.584 |
| 1.432 | 373.38 | 1.392 | -0.023 | 13.446 | 0.147 | 115.783 | -35441 | 23.040 | 0.85 | -44488.66 | -6.789 | -2.860 | 7.610 | -4.824 | -9.869 | 3.588 |
| 1.431 | 387.41 | 1.361 | 0.463 | 13.446 | 0.124 | 118.840 | -37291 | 24.038 | 1.00 | -45559.18 | -6.755 | -2.830 | 7.622 | -4.792 | -10.323 | 3.587 |
| 1.617 | 401.43 | 1.333 | 0.880 | 13.446 | 0.122 | 121.877 | -39133 | 25.037 | 0.87 | -46629.69 | -6.737 | -2.815 | 7.851 | -4.776 | -10.770 | 3.583 |
| 1.396 | 415.46 | 1.307 | 1.298 | 13.446 | 0.125 | 124.904 | -40938 | 26.035 | 1.00 | -47700.21 | -6.726 | -2.806 | 7.404 | -4.766 | -11.219 | 3.581 |
| 1.774 | 429.49 | 1.285 | 1.715 | 13.446 | 0.123 | 127.929 | -42741 | 27.034 | 0.88 | -48770.72 | -6.718 | -2.800 | 7.592 | -4.759 | -11.493 | 3.580 |
| 1.576 | 387.41 | 1.359 | 0.295 | 13.727 | 0.170 | 125.653 | 32749 | 24.038 | 0.85 | -45559.13 | -6.662 | -2.597 | 9.093 | -4.630 | -10.361 | 5.547 |
| 1.662 | 401.43 | 1.332 | 0.513 | 13.924 | 0.133 | 119.540 | 34963 | 25.037 | 0.85 | -46629.51 | -6.622 | -2.510 | 8.816 | -4.566 | -10.973 | 4.855 |
| 1.548 | 427.47 | 1.390 | 1.187 | 13.924 | 0.132 | 137.258 | 38586 | 27.034 | 0.87 | -48737.89 | -6.568 | -2.518 | 9.352 | -4.543 | -11.196 | 5.527 |
| 1.349 | 435.45 | 1.394 | 1.372 | 13.446 | 0.198 | 116.706 | 37256 | 28.033 | 1.00 | -49709.30 | -6.727 | -2.954 | 7.714 | -4.840 | -10.027 | 3.355 |
| 1.775 | 421.42 | 1.452 | 1.302 | 13.445 | 0.200 | 120.216 | 35363 | 27.034 | 0.87 | -48639.18 | -6.780 | -2.942 | 7.562 | -4.861 | -10.073 | 3.668 |
| 1.956 | 328.38 | 1.281 | 0.763 | 13.276 | 0.114 | 92.524 | 24667 | 20.045 | 0.85 | -38920.18 | -6.775 | -2.892 | 6.000 | -4.833 | -9.405 | 3.405 |
| 1.585 | 342.41 | 1.255 | 1.102 | 13.276 | 0.148 | 95.753 | 26366 | 21.043 | 1.00 | -39990.78 | -6.726 | -2.848 | 6.040 | -4.787 | -9.886 | 3.413 |
| 1.817 | 356.44 | 1.231 | 1.588 | 13.276 | 0.123 | 98.816 | 27990 | 22.041 | 0.87 | -41061.30 | -6.692 | -2.818 | 5.839 | -4.755 | -10.339 | 3.412 |
| 1.745 | 370.46 | 1.211 | 2.005 | 13.276 | 0.127 | 101.852 | 29614 | 23.040 | 1.00 | -42131.81 | -6.674 | -2.804 | 5.943 | -4.739 | -10.624 | 3.408 |
| 1.751 | 384.49 | 1.192 | 2.422 | 13.276 | 0.124 | 104.880 | 31205 | 24.038 | 0.88 | -43202.32 | -6.662 | -2.795 | 5.928 | -4.729 | -11.235 | 3.407 |
| 1.815 | 398.52 | 1.176 | 2.840 | 13.276 | 0.121 | 107.905 | 32800 | 25.037 | 1.00 | -44272.83 | -6.655 | -2.789 | 6.160 | -4.722 | -11.684 | 3.406 |
| 1.618 | 356.44 | 1.230 | 1.420 | 13.557 | 0.144 | 92.273 | 28274 | 22.041 | 1.00 | -41061.36 | -7.172 | -2.857 | 6.204 | -5.014 | -10.371 | 3.384 |
| 1.574 | 404.48 | 1.275 | 2.496 | 13.401 | 0.199 | 96.369 | 33194 | 26.035 | 0.88 | -45211.74 | -6.586 | -2.854 | 6.211 | -4.720 | -10.412 | 3.284 |
| 1.850 | 390.45 | 1.324 | 2.427 | 13.276 | 0.200 | 100.248 | 31175 | 25.037 | 1.00 | -44141.30 | -6.716 | -2.869 | 5.375 | -4.793 | -10.089 | 3.649 |
Table 2. Values of the calculated parameters obtained by DFT/B3LYP 6-31G* optimization of the studied compounds.
Results and Discussion
This study was carried for a series of 36 compounds of 5-N-substituted-2-(substituted benzenesulphonyl) glutamines, in order to determine a quantitative relationship between the structural information and the antitumor activity (IT) of these glutamines compounds.
The set of sixteen descriptors encoding the 36 compounds of 5-N-substituted-2-(substituted benzenesulphonyl) glutamines, electronic, energetic and topologic parameters are submitted to PCA analysis [32]. The first three principal axes are sufficient to describe the information provided by the data matrix. Indeed, the percentages of variance are 30.36%, 20.95% and 15.95% for the axes F1, F2 and F3, respectively. The total information was estimated to a percentage of 67.26%. The principal component analysis (PCA) [33,34] was conducted to identify the link between the different variables. Bold values are different from 0 at a significance level of p=0.05. The Pearson correlation coefficients were summarized in the following Table 3. The obtained matrix provides information on the negative or positive correlation between variables.
| Log (IT) | MW | D | LogP | Eb | ChM | Es | Ee | ShA | ShC | Et | EHOMO | ELUMO | m | χ | TNC | Ea | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Log (IT) | 1 | ||||||||||||||||
| MW | -0.143 | 1 | |||||||||||||||
| D | -0.214 | 0.160 | 1 | ||||||||||||||
| LogP | 0.244 | 0.402 | -0.683 | 1 | |||||||||||||
| Eb | -0.252 | 0.463 | 0.261 | -0.206 | 1 | ||||||||||||
| Char. | -0.087 | 0.300 | 0.386 | 0.166 | -0.124 | 1 | |||||||||||
| Es | -0.039 | 0.442 | 0.356 | -0.210 | 0.435 | -0.009 | 1 | ||||||||||
| Ee | 0.210 | -0.044 | -0.313 | 0.453 | -0.166 | 0.282 | -0.558 | 1 | |||||||||
| ShA | -0.128 | 0.995 | 0.150 | 0.450 | 0.416 | 0.374 | 0.408 | 0.002 | 1 | ||||||||
| ShC | 0.112 | 0.037 | -0.229 | 0.248 | -0.334 | 0.065 | -0.038 | 0.106 | 0.055 | 1 | |||||||
| Et | 0.189 | -0.965 | -0.381 | -0.162 | -0.528 | -0.302 | -0.519 | 0.167 | -0.949 | 0.019 | 1 | ||||||
| EHOMO | -0.049 | 0.371 | 0.102 | 0.057 | 0.300 | 0.050 | 0.643 | -0.353 | 0.363 | -0.219 | -0.366 | 1 | |||||
| ELUMO | -0.151 | 0.165 | -0.334 | 0.225 | 0.409 | -0.243 | -0.335 | 0.330 | 0.144 | -0.095 | -0.096 | -0.194 | 1 | ||||
| m | -0.237 | 0.340 | 0.537 | -0.560 | 0.686 | -0.091 | 0.474 | -0.412 | 0.281 | -0.268 | -0.503 | 0.338 | -0.014 | 1 | |||
| χ | -0.170 | 0.357 | -0.264 | 0.245 | 0.552 | -0.205 | 0.028 | 0.124 | 0.333 | -0.209 | -0.290 | 0.355 | 0.848 | 0.169 | 1 | ||
| TNC | 0.013 | -0.614 | 0.516 | -0.618 | -0.408 | 0.336 | -0.134 | -0.071 | -0.582 | -0.003 | 0.477 | -0.229 | -0.498 | -0.059 | -0.598 | 1 | |
| Ea | -0.240 | 0.158 | 0.183 | -0.209 | 0.640 | -0.169 | -0.010 | 0.210 | 0.115 | -0.317 | -0.213 | 0.049 | 0.619 | 0.426 | 0.616 | -0.296 | 1 |
A strong correlation is observed between MW and ShA (r=0.995), high a negative correlation is between MW and Et (r=-0.965), and a high correlation is observed between ShA and Et (r=-0,945)
Table 3. Correlation matrix (Pearson (n)) between different obtained descriptors.
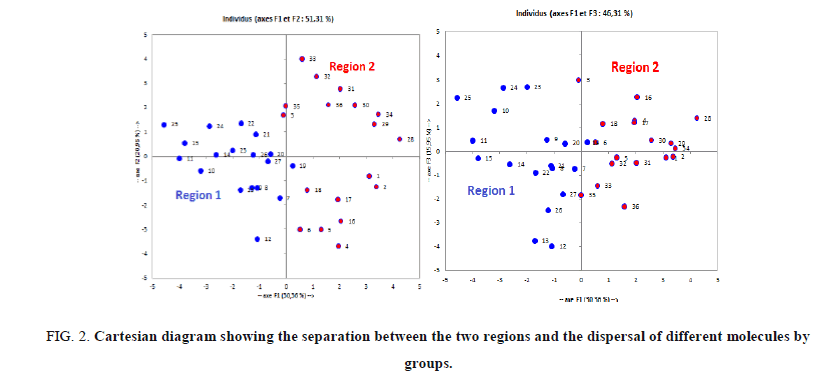
Analysis of projections according to the planes F1-F2 and F1-F3 (51.31% and 46.31% of the total variance respectively) of the studied molecules (Figure 2) shows that the molecules are dispersed in two regions: Region 1 contains compounds having a values of total energy Et between -49709.561 (eV) and -45559.132 (eV), region 2 contains compounds having a values of total energy Et between -45211.746 (eV) and -38920.188 (eV).
Figure 2: Cartesian diagram showing the separation between the two regions and the dispersal of different molecules by groups.
Multiple linear regressions (MLR)
To establish quantitative relationships between the inhibition of tumor weight log (IT) and selected descriptors, our array data were subjected to a multiple linear regression. Only variables whose coefficients are significant were retained.
Modeling the inhibition of tumor cells log (IT) value of all training compounds (5-N-substituted 2-(substituted benzenesulphonyl) glutamines) led to the best value corresponding to the linear combination of the following descriptors: Partition coefficient log P, Mulliken charges ChM, steric energy Es, dipole moment µ, absolute electronegativity χ, total negative charges of the molecule TNC, activation energy Ea.
The most significant QSAR model was obtained, as shown in the following equation:
Log (IT)=2, 34+0, 45 × logP-7, 03 × ChM+1, 57 × 10-03 Es+8, 08 ×10-02 × µ-0, 66 × χ+0, 46 × TNC+0, 15 × Ea (5)
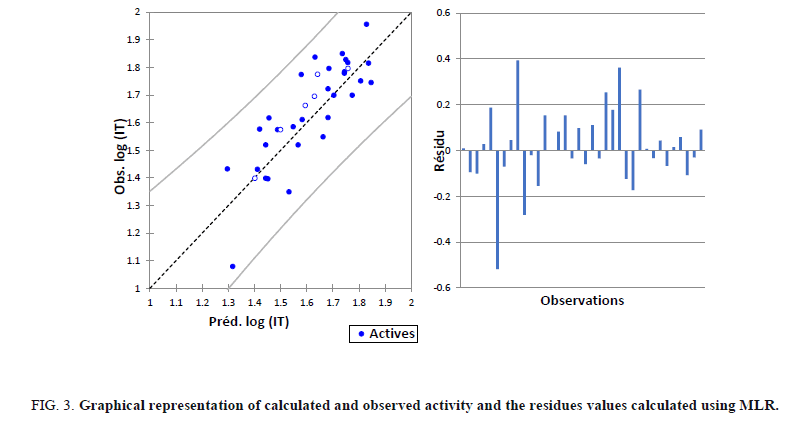
For our 30 compounds, the correlation between experimental and calculated log (IT) one based on this model are quite significant (Figure 3) as indicated by statistical values:
Figure 3: Graphical representation of calculated and observed activity and the residues values calculated using MLR.
N=30 R2=0.626 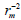 =0.606
=0.606 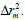 =0.184 F=5.255 RMSE=0.134 P<0.0001
=0.184 F=5.255 RMSE=0.134 P<0.0001
In the above regression equation, N is number of compounds, R is correlation coefficient, F is Fisher’s test, RMSE is root mean square error and P is the significance level. Generally, the higher the correlation coefficient and the lower the standard error, the more reliable is the model. High values of F and P is much smaller than 0.05 indicate the significance of eqn. (5), which reflects the ratio of variance explained by the model and the variance due to the error in the model. Based on eqn. (5), the positive correlation coefficient for log P, Es, μ, TNC and Ea indicates that a compound with a larger value for these descriptors would have a larger log (IT) value (increase inhibition of tumor cells), the negative correlation for ChM and χ indicate that a compound with a larger value for these descriptors would have a smaller log (IT) value (decrease inhibition of tumor cells).
The correlations of predicted and observed activities and the residual values are illustrated in Figure 3.
The Figure 3 shows a very regular distribution of Log (IT) values depending on the experimental values.
As part of this conclusion, we can say that the inhibition of tumor cells Log (IT) values obtained from MLR are good correlated to that of the observed values.
In this work, variance inflation factors (VIF) was calculated to test if multicollinearities existed among the descriptor which is defined as:
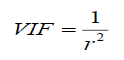 (6)
(6)
Where, r is the correlation coefficient of multiple regression between one independent variable and the others. If VIF=1, no self-correlation exists among each variable, when VIF ranges from 1.0 to 5.0, the correlation equation is acceptable; if VIF>10.0, the regression equation is unstable and recheck is necessary. As can be seen from Table 4, the VIF values of the five descriptors are all less than 5 and two descriptors are not more than 10, indicating that there is no multicollinearity among the selected descriptors and the resulting model has good stability.
| Descriptor | VIF | SR | t-test value |
|---|---|---|---|
| Log P | 8.780 | 0.386 | 5.027 |
| ChM | 2.499 | 0.206 | -4.694 |
| Es | 1.789 | 0.174 | 3.004 |
| m | 3.177 | 0.232 | 1.859 |
| χ | 2.496 | 0.206 | -2.159 |
| TNC | 8.558 | 0.382 | 4.498 |
| Ea | 3.051 | 0.228 | 2.551 |
Table 4. VIF, SR and t test value of descriptors in QSAR model.
In order to distinguish the importance of each descriptor on antitumor of glutamines, standard regression coefficients (SR) and t test values of the seven descriptors are also listed in Table 4. As shown in Table 4, the absolute value of SR and t test value of log P are 0.386 and 5.027, respectively, both larger than the other descriptors, which indicates that in this QSAR model, the influence of Log P on antitumor cells is stronger than that of the others.
Descriptors analysis and interpretation
Based on the eqn. (5), we would attempt to explain mechanisms of the inhibitory tumor activity of the 5-N-substituted 2-(substituted benzenesulphonyl) glutamines, in the following:
Partition coefficient (Log P) appeared as the most significant descriptor for the derived QSAR model, it’s the most important descriptor for the anticancer cells. The developed model suggests that higher lipophilicity results in good percentage tumor inhibition. Lipophilicity is very important for glutamine compounds to permeate, transport to and bioaccumulate in tumor cells. The diffusion of glutamine compounds across biological membranes is regulated by both the lipid membrane and the nonmoving aqueous solvent layer at both the inside and outside surfaces of the membrane. Glutamine compounds with higher Log P are more likely to give better anticancer activity.
Total negative charges TNC follows Log P, also is a good significant descriptor of this model. The magnitude of TNC may characterize atomic charges, which are related to the reactive centers of chemical compounds. TNC showed that decreasing the atomic charge produces stronger binding to the active site and therefore potentially enhancing anticancer activity. So, glutamine compounds with lower TNC have stronger electron-donating groups on phenyl rang, marginally contributing to the activity.
Dipole moment µ characterizes the average charge separation in a molecular system, and can represent the electronic information of compounds. Furthermore, µ can partially reflect molecular polarity and it may be having favorable contribution towards the antitumor value as evidenced by the positive regression coefficient. The higher µ value, the easier these glutamines to participate in certain dipole-dipole or polar types of interaction with targets in cells and leading to greater anticancer activity. Activation energy Ea is influencing by the temperature of the system and the energy of repulsion between the reacting centers and this energy is affected the charge distribution on the reacting centers, the inhibitory tumor activity is varying positively with the activation energy Ea of the substituted glutamines. Steric energy Es dependent to the steric effect of substituent groups of glutamines, this effect of substituents on the charge distribution is discussed in terms of the molecular orbital method, an attempt being made to distinguish between the influence on the π electrons of the inductive and mesomeric effect of substituents of glutamines, we can say the steric bulk at the R5 position and at the aromatic rand may not be useful for the activity or may be detrimental to the activity, and the length of the some groups like R5 substituent is also marginally contributing to the activity, that explain smaller groups at the R5 position or at the aromatic rang may give the better ligand fit into the active site.
The descriptors proposed in eqn. (5) by MLR were, therefore, used as the input parameters in the multiples nonlinear regression (MNLR) and artificial neural network (ANN).
Multiple nonlinear regression (MNLR)
We have used also the technique of nonlinear regression model to improve the predicted activity in a quantitative way. It takes into account several parameters. This is the most common tool for the study of multidimensional data. We have applied to the data matrix constituted obviously from the descriptors proposed by MLR corresponding to the 30 glutamines compounds used in training set.
The resulting equation is:
Log (IT)=-89, 94+0, 53 × Log P+3, 89 × ChM+3, 63E-03 × Es+0, 97 × μ-39, 69 × χ+1, 34 × TNC-0, 32 × Ea+9, 43 × 10-3 × (LogP)2-36, 99 × (ChM)2-4,50 × 10-6 × (Es)2-6, 35 × 10-2 × (μ)2-4,06 × (χ)2+3,85 × 10-2 × (TNC)2+8,11 × 10-2 × (Ea)2 (7)
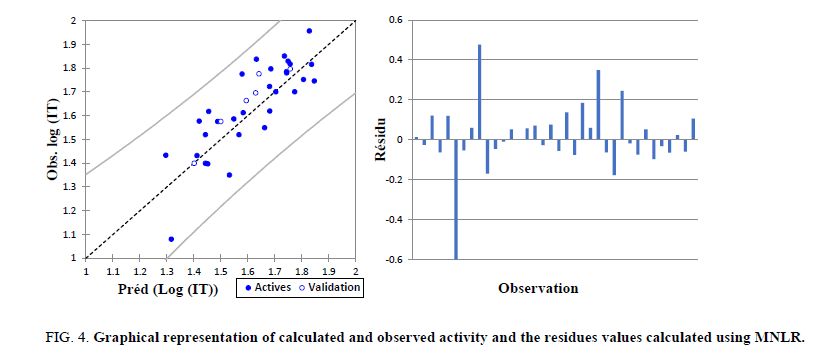
N=30, R2=0.792>0.6, 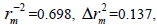 RMSE=0.121
RMSE=0.121
The correlations of predicted and observed activities and the residual values are illustrated in Figure 4.
Figure 4: Graphical representation of calculated and observed activity and the residues values calculated using MNLR.
Artificial neural networks (ANN)
The ANN has become an important and widely used nonlinear modeling technique for QSAR studies, it can be used to generate predictive models of quantitative structure-activity relationships (QSAR) between a set of molecular descriptors obtained from the MLR and observed values of antitumor activity Log (IT).
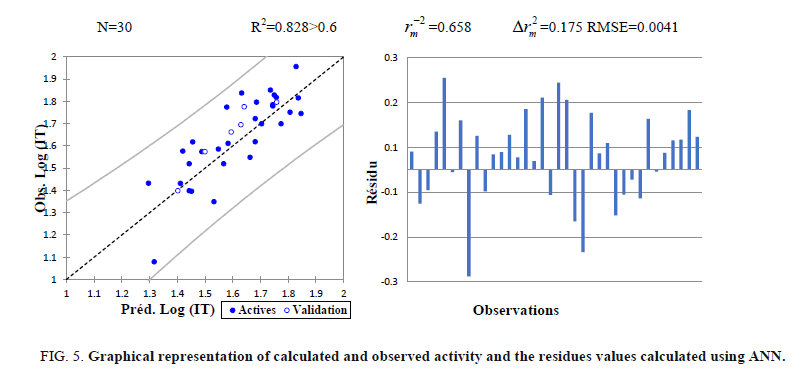
The correlations coefficients and standard error of estimate, obtained with the ANN, show that the selected descriptors by MLR are pertinent and that the model proposed to predict the anticancer activity is relevant. The correlation between ANN calculated and experimental activities and the residues values are very significant as illustrated in Figure 5 and as indicated by R and R2 values.
Figure 5: Graphical representation of calculated and observed activity and the residues values calculated using ANN.
The values of predicted activities calculated using ANN and the observed values are given in Table 5.
| Methods | Leave many-out cross-validation | Test set | ||||
|---|---|---|---|---|---|---|
| N | R | R2 | N | R | R2 | |
| MLR | 30 | 0.799 | 0.636 | 6 | 0.816 | 0.662 |
| MNLR | 30 | 0.777 | 0.604 | 6 | 0.830 | 0.690 |
| ANN | 30 | 0.871 | 0.760 | 6 | 0.900 | 0.821 |
Table 5. Performance comparison between models obtained by MLR, RNLM and ANN.
Model validation
In order to check the reliability and the stability of the QSAR model elaborated by the MLR, MNLR and ANN methods, we have used the internal and external validations. The leave-many-out cross-validation of three models, showing the good robustness of the model. Moreover, predictions realized on the test set were in good agreement with the experimental values. True predictive power of a QSAR model is to test their ability to predict accurately the anticancer activity of glutamine compounds from an external test set: 6-9-16-24-27-35, (compounds which were not used for the model development).
The comparison of the values of log (IT-test) to log (IT-obs) shows that a good prediction has been obtained for the 6 compounds. The main performance parameters of the three models are shown in Table 5.
Applicability domain
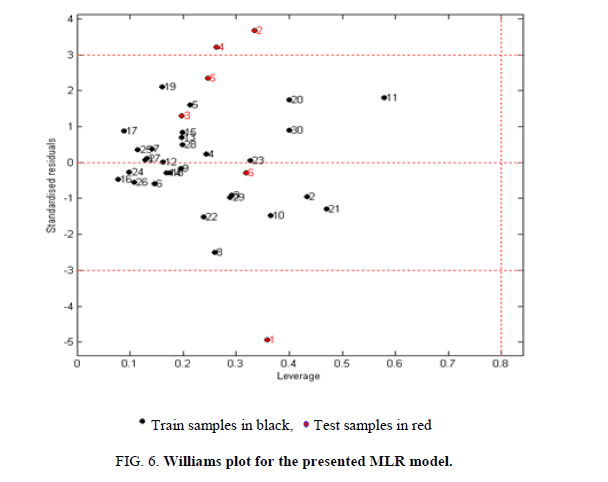
The AD is an important tool for reliable application of QSAR models, while characterization of interpolation space is significant in defining the AD. We have reported that the web application can be easily used for identification of the Xoutliers for training set compounds and detection of the test compounds residing outside the applicability chemical domain using the descriptor pool of the training and test sets. The selected four molecular descriptors in this model were used for the calculation of the leverage values: 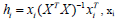 namely row vector of descriptors of compound i, X called Matrix of model deducted from the descriptors of training set and T correspondent to Matrix transposed.
namely row vector of descriptors of compound i, X called Matrix of model deducted from the descriptors of training set and T correspondent to Matrix transposed.
The critical leverage h* is fixed at (3P+1)/N or P and N are respectively the number of descriptors and number of compounds of training set. If h>h*, the prediction of the compound can be considered as unreliable and vice versa. As illustrated in the Williams graph of Figure 6, excepting the compounds 6, 9 and 24 are outside (has standardized residual less or more than standard deviation units (± 3?), the majority of the molecules in the training and test sets (91.66%) fall within the applicability chemical domain and then the predicted inhibitory activity by the developed QSAR model is reliable.
Y-Randomization
In this test, random RML, RNLM and ANN models are generated by randomly shuffling the dependent variable while keeping the independent variables as it is. The new QSAR models are expected to have significantly low R2 and Q2 values for several trials, which confirm that the developed QSAR models are robust and the results of the RML, RNLM and ANN methods are not due to a chance correlation of the training set.
A comparison of the quality of MLR, MNLR and ANN models shows that the ANN is the best models that indicate the effects of these descriptors on the biological activity of the studied compounds (Table 6).
| Iteration | MLR | MNLR | ANN | |||||
|---|---|---|---|---|---|---|---|---|
| Q2 | R2 | Q2 | R2 | Q2 | R2 | |||
| 1 | 0.421 | 0.540 | 0.435 | 0.476 | 0.435 | 0.440 | ||
| 2 | 0.347 | 0.407 | 0.389 | 0.390 | 0.279 | 0.530 | ||
| 3 | 0.291 | 0.301 | 0.279 | 0.321 | 0.299 | 0.371 | ||
| 4 | 0.161 | 0.251 | 0.198 | 0.254 | 0.223 | 0.451 | ||
| 5 | 0.369 | 0.464 | 0.317 | 0.592 | 0.217 | 0.364 | ||
Table 6. Y-Randomization validation results of the CoMFA and CoMSIA models (Q2 and R2 values after several Y-randomization tests).
All the results discussed above showed that the presented MLR, MNLR and ANN models could be effectively used to predict the Log (IT) of 5-N-substituted-2-(substituted benzenesulphonyl) glutamines compounds with different substitutions, they were able to establish a satisfactory relationship between the molecular descriptors and the antitumor activity of the studied compounds.
From the values of correlation coefficient of the six compounds (test set), the cross-validated coefficient (training set) and other statistical parameters of these methods (MLR, MNLR and ANN), it is clear that the predictive power of our models are equally robust and stable, it can be efficiently used for estimating the antitumor activity of other some glutamine compounds for which no experimental data are available.
The predicted antitumor activity values of 5-N-substituted-2-(substituted benzenesulphonyl) glutamines compounds of training set, obtained by different methods are listed in Table 7 along with their observed activity.
| No. | Log (IT) | ||||||
|---|---|---|---|---|---|---|---|
| Observed | RML | MNLR | ANN | ||||
| Predicted | Residue | Predicted | Residue | Predicted | Residue | ||
| 1 | 1.722 | 1.713 | 0.009 | 1.709 | 0.013 | 1.682 | 0.040 |
| 2 | 1.699 | 1.793 | -0.094 | 1.725 | -0.026 | 1.775 | -0.076 |
| 3 | 1.398 | 1.499 | -0.101 | 1.277 | 0.121 | 1.443 | -0.045 |
| 4 | 1.574 | 1.546 | 0.028 | 1.638 | -0.064 | 1.489 | 0.085 |
| 5 | 1.837 | 1.650 | 0.187 | 1.718 | 0.119 | 1.632 | 0.205 |
| 6* | 1.398 | 1.916 | -0.518 | 1.999 | -0.601 | 1.402 | -0.004 |
| 7 | 1.699 | 1.770 | -0.071 | 1.753 | -0.054 | 1.704 | -0.005 |
| 8 | 1.796 | 1.751 | 0.045 | 1.737 | 0.059 | 1.686 | 0.110 |
| 9* | 1.796 | 1.403 | 0.393 | 1.319 | 0.477 | 1.758 | 0.038 |
| 10 | 1.079 | 1.360 | -0.281 | 1.250 | -0.171 | 1.317 | -0.238 |
| 11 | 1.519 | 1.539 | -0.020 | 1.565 | -0.046 | 1.443 | 0.076 |
| 12 | 1.519 | 1.673 | -0.154 | 1.529 | -0.010 | 1.568 | -0.049 |
| 13 | 1.779 | 1.626 | 0.153 | 1.727 | 0.052 | 1.745 | 0.034 |
| 14 | 1.784 | 1.783 | 0.001 | 1.782 | 0.002 | 1.745 | 0.039 |
| 15 | 1.828 | 1.746 | 0.082 | 1.772 | 0.056 | 1.750 | 0.078 |
| 16* | 1.695 | 1.542 | 0.153 | 1.625 | 0.070 | 1.630 | 0.065 |
| 17 | 1.611 | 1.646 | -0.035 | 1.638 | -0.027 | 1.583 | 0.028 |
| 18 | 1.432 | 1.334 | 0.098 | 1.356 | 0.076 | 1.297 | 0.135 |
| 19 | 1.431 | 1.491 | -0.060 | 1.487 | -0.056 | 1.412 | 0.019 |
| 20 | 1.617 | 1.506 | 0.111 | 1.481 | 0.136 | 1.456 | 0.161 |
| 21 | 1.396 | 1.431 | -0.035 | 1.472 | -0.076 | 1.452 | -0.056 |
| 22 | 1.774 | 1.521 | 0.253 | 1.590 | 0.184 | 1.579 | 0.195 |
| 23 | 1.576 | 1.399 | 0.177 | 1.517 | 0.059 | 1.420 | 0.156 |
| 24* | 1.662 | 1.301 | 0.361 | 1.313 | 0.349 | 1.595 | 0.067 |
| 25 | 1.548 | 1.672 | -0.124 | 1.611 | -0.063 | 1.663 | -0.115 |
| 26 | 1.349 | 1.522 | -0.173 | 1.527 | -0.178 | 1.533 | -0.184 |
| 27* | 1.775 | 1.509 | 0.266 | 1.530 | 0.245 | 1.642 | 0.133 |
| 28 | 1.956 | 1.949 | 0.007 | 1.974 | -0.018 | 1.829 | 0.127 |
| 29 | 1.585 | 1.618 | -0.033 | 1.660 | -0.075 | 1.549 | 0.036 |
| 30 | 1.817 | 1.774 | 0.043 | 1.765 | 0.052 | 1.758 | 0.059 |
| 31 | 1.745 | 1.812 | -0.067 | 1.843 | -0.098 | 1.847 | -0.102 |
| 32 | 1.751 | 1.736 | 0.015 | 1.784 | -0.033 | 1.807 | -0.056 |
| 33 | 1.815 | 1.757 | 0.058 | 1.880 | -0.065 | 1.837 | -0.022 |
| 34 | 1.618 | 1.726 | -0.108 | 1.595 | 0.023 | 1.682 | -0.064 |
| 35* | 1.574 | 1.604 | -0.030 | 1.633 | -0.059 | 1.501 | 0.073 |
| 36 | 1.850 | 1.759 | 0.091 | 1.745 | 0.105 | 1.736 | 0.114 |
*Test set
Table 7. Observed, predicted Log (IT) and residue according to different methods.
Conclusion
In present work, we have carried out a comparative analysis of % inhibition of tumor weight log (IT) of glutamine compounds by three QSAR approaches, MLR, MNLR and ANN. Both approaches have showed good predictive power. Comparison of the qualities of MLR, MNLR and ANN models shown that the ANN has a good predictive ability and strong robustness than the MLR, yields a regression model with improved predictive power, we have established a relationship between several descriptors and the % inhibition of tumor weight log (IT). The predictive ability and robustness of the obtained models were assessed by cross-validation, and external validation through test set. Thus, the model could be efficiently employed for estimating the antitumor activity and for select the descriptors which have an impact on this biological activity and which are sufficiently rich in chemical, electronic and topological information to encode the structural feature.
The present study shows that molecular descriptors, namely the partition coefficient log P, Mulliken charges ChM, steric energy Es, dipole moment µ, absolute electronegativity χ, total negative charges of the molecule TNC, activation energy Ea, are useful for the prediction of the best % Inhibition of Tumor cells of 5-N-substituted-2-(substituted benzenesulphonyl) glutamines compounds, which the experimental data are unavailable.
The QSAR model is statistically significant, robust and can be used for prediction the activity more accurately, it may be helpful for a better understanding of the anticancer activity of this class of compounds and useful as guidance to estimate the antitumor cells as biological activity of new glutamine compounds.
Acknowledgment
We are grateful to the “Association Marocaine des Chimistes Théoriciens” (AMCT) for its pertinent help concerning the programs.
References
- Kamal A, Balakishan G, Ramakrishna G. et al. Synthesis and biological evaluation of cinnamido linked pyrrolo [2, 1-c] [1,4] benzodiazepines as antimitotic agents. Eur J Med Chem. 2010;45:3870-84.
- Costa C, Huneau JF, Tome D. Characteristics of L-glutamine transport during Caco-2 cell differentiation. Biochem Biophys Acta/Biomembranes. 2000;95:1509.
- Zalkin H, Smith JL. Enzymes utilizing glutamine as an amide donor. Adv Enzymol Relat Areas Mol Biol. 1998;72:87.
- Srikanth K, Debnath B. Syntheses, biological evaluation and QSAR study on antitumor activity of 1, 5-N, N′-disubstituted-2-(substituted benzenesulphonyl) glutamamides. T Jha Bioorg Med Chem. 2002;10:1841-54.
- Goodarzi M, Freitas MP, Jensen R. Ant colony optimization as a feature selection method in the QSAR modeling of anti-HIV-1 activities of 3-(3, 5-dimethylbenzyl) uracil derivatives using MLR, PLS and SVM regressions. Chemom Intell Lab Syst. 2009;98:123.
- Shen Q, Jiang JH, Jiao CX, et al. Modified particle swarm optimization algorithm for variable selection in MLR and PLS modeling: QSAR studies of antagonism of angiotensin II antagonists. Eur J Pharm Sci. 2004;22:145.
- Blum BJW, Speece RE. Quantitative structure-activity relationships for chemical toxicity to environmental bacteria. Ecotoxicol Environ Safety. 1991;22:198.
- Burden FR, Winkler DA. A quantitative structure-activity relationships model for the acute toxicity of substituted benzenes to Tetrahymena pyriformis using Bayesian-regularized neural networks. Chem Res Toxicol. 2000;13:436.
- Estrada E. On the topological sub-structural molecular design (TOSS-MODE) in QSPR/QSAR and drug design research. SAR QSAR Environ Res. 2000;11:55.
- Ivan D, Crisan L, Funar-Timofei S, et al. A quantitative structure-activity relationships study for the anti-HIV-1 activities of 1-(2-hydroxyethoxy) methyl-6-(phenylthio) thymine derivatives using the multiple linear regression and partial least squares methodologies. J Serb Chem Soc. 2013;78:495.
- Fatemi MH, Malekzadeh H. Prediction of log(IGC50)-1 for benzene derivatives to ciliate Tetrahymena pyriformis from their molecular descriptors. Bull Chem Soc Jpn. 2010;83:233.
- Cronin MTD, Gregory BW, Schultz TW. Quantitative structure-activity analyses of nitrobenzene toxicity to Tetrahymena pyriformis. Chem Res Toxicol. 1998;11:902.
- Sarkar U, Parthasarathi R, Subramanian V, et al. Toxicity analysis of polychlorinated dibenzofurans through global and local electrophilicities. J Mol Struct THEOCHEM. 2006;758:119-25.
- Srikanth K, Kumar CA, Ghosh B, et al. Synthesis, screening and quantitative structure-activity relationship (QSAR) studies of some glutamine analogues for possible anticancer activity. Bioorg Med Chem. 2002;10:2119-31.
- Frisch MJ. Gaussian 03, M J Revision B.01 Gaussian Inc Pittsburgh, PA. 2003.
- Lee C, Yang W, Parr RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys Rev. 1988;37:785-9.
- Elidrissi B, Ousaa A, Ghamali M, et al. Combining DFT and QSAR result for predicting the biological activity of 1-(2-ethoxyethyl)-1H-pyrazolo[4,3-d] pyrimidines as phosphodiesterase V inhibitors. J Com Meth in Molec Desig. 2014;4(4):140-9.
- Elidrissi B, Ousaa A, Ghamali M, et al. The acute toxicity of nitrobenzenes to Tetrahymena pyriformis: Combining DFT and QSAR studies. Mor J of Chemis. 2015;3(4):848-60.
- Chtita S, Larif M, Ghamali M, et al. Studies of two different cancer cell lines activities (MDAMB-231 and SK-N-SH) of imidazo [1, 2-a] pyrazine derivatives by combining DFT and QSAR results. IJIRSET. 2013;2(11):6586-601.
- Ousaa A, Elidrissi B, Ghamali M, et al. Acute toxicity of halogenated phenols: Combining DFT and QSAR studies. JCMMD. 2014;4(3):10-8.
- Elidrissi B, Ousaa A, Ghamali M, et al. The biological activity of pyrazine carboxamides derivatives as an herbicidal agent: Combining DFT and QSAR studies. JCMMD. 2015;5(2):83-91.
- Hmamouchi R, Larif M, Adad A, et al. Structure activity and prediction of biological activities of compound (2-methyl-6-phenylethynylpyridine) derivatives relationships rely on electronic and topological descriptors. JCMMD. 2014;4(3):61-71.
- Wang D, Yuan Y, Duan S, et al. QSPR study on melting point of carbocyclic nitroaromatic compounds by multiple linear regression and artificial neural network. Chem Inte Labo Sys. 2015;143:7-15.
- Efron B. Estimating the error rate of a prediction rule: improvement on cross-validation. Stat Assoc J Am. 1983;78:316-31.
- Efroymson MA, Ralston A, Wilf HS. Multiple Regression Analysis in Mathematical Methods for Digital Computers. Wiley New York. 1960.
- Osten DW. Selection of optimal regression models via cross-validation. J Chemom. 1998;2:39-48.
- Roy K, Mitra I, Kar S, et al. Comparative studies on some metrics for external validation of QSPR models. J Chem Inf Model. 2012;52:396-408.
- Ojha PK, Mitra I, Das R, et al. Further exploring rm2 metrics for validation of QSPR models. Chemom Intell Lab Syst. 2011;107:194-205.
- Rücker C, Rücker G, Meringer M. Y-Randomization and its variants in QSPR/QSAR. J Chem Infor and Mod. 2007;47:2345-57.
- Lee PY, Chen CYJ. Impact of cadmium on the bacterial communities in the gut of Metaphire posthuma. Hazard. Mater. 2009;165:156-61.
- McKim J, Schmieder P, Veith G. Absorption dynamics of organic chemical transport across trout gills as related to octanol-water partition coefficient. Toxicol Appl Pharm. 1985; 77: 1-10.
- Niu JF, Yu G. Molecular structural characteristics governing biocatalytic oxidation of PAHs with hemoglobin. Environ Toxicol Phar. 2004;18:39-45.
- Zhang HJ, Zhang JY, Zhu YM. In vitro investigations for the QSAR mechanism of lymphocytes apoptosis induced by substituted aromatic toxicants. Fish Shellfish Immun. 2008;25:710-7.
- Roy K, Kar S, Ambure P. On a simple approach for determining applicability domain of QSAR models. Chem Intel Labor Syst. 2015;145:22-9.