Original Article
, Volume: 15( 3)Radiation and Chemical Reaction Effects on MHD Free Convective Heat and Mass Transfer Flow of a Viscoelastic Fluid Past a Porous Plate with Heat Generation/Absorption
- *Correspondence:
- Ramana Murthy MV, Department of Mathematics and Computer Science, Osmania University, Hyderabad, Tel: 040-2768 2444; E-mail: mv.rm50@gmail.com
Received: May 02, 2017; Accepted: August 03, 2017; Published: August 07, 2017
Citation: Santhosha B, Younus S, Kamala G, et al. Radiation and Chemical Reaction Effects on MHD Free Convective Heat and Mass Transfer Flow of a Viscoelastic Fluid Past a Porous Plate with Heat Generation/Absorption. Int J Chem Sci. 2017;15(3):170
Abstract
Radiation and chemical combined effects on MHD free convective heat and mass transfer flow of viscous, incompressible, conducting elastic fluid through porous medium finite by a porous plate within the presence of heat generation/absorption is studied. The momentum, energy and mass diffusion equations are coupled non-linear partial differential equations; these are solved by applying two term perturbation methodology and mistreatment software system MATLAB. The options of the fluid flow, heat and mass transfer characteristics are analyzed by plotting graphs and mentioned qualitatively.
Keywords
MHD; Chemical reaction; Radiation; Viscoelastic; Skin-friction; Porous medium
Introduction
The heat and mass transfer in free convective through porous media has been broadly investigated in the current years due to its applications in engineering. The study of non-Newtonian fluid flow by engineers and experts has risen in recent times due to its useful application in various fields. Keeping its importance in mind an extensive range of mathematical models has been established to simulate the various hydrodynamic behaviors of these non-Newtonian fluids. Various viscoelastic fluids classical like the Rivlin-Ericksen 2nd order model, Oldroyd model and Johnson-Seagalman model. The fluid, which exhibits the elasticity property of solids and viscous property of liquids are called viscoelastic fluid. Fluid models of this type come across petrochemical, biomedical and environmental engineering including polypropylene combination sintering.
Beard and Walter [1] had presented the boundary layer treatment for unidealized viscoelastic fluid. The heat transfer in convection flow of viscoelastic fluid of Walter model was investigated by Rajagopal [2]. Ibrahim [3] discussed the effects of the radiation and chemical reaction on the unsteady MHD convection flow through semi-infinite vertical porous plate with heat source and suction.
Muthucumaraswamy and Ganesan [4] studied the unsteady flow thorugh impulsively semi-infinite vertical plate, which subjected to uniform heat flux of a chemical reaction effect. Chamkha [5] was studied the MHD flow of a numerical of uniformly stretched vertical permeable surface in the presence of heat and chemical reaction. Chamkha [6] discussed unsteady convective heat and mass transfer through semi-infinite porous plate with heat absorption. Hossain [7] were analyzed natural convection flow of a vertical surface with uniform temperature in the presence of heat generation/absorption. Hady [8] are studied the problem of free convection flow along a vertical wavy surface embedded in electrically conducting fluid saturated porous media in the presence of internal heat generation or absorption effect. Mohamed [9] has discussed double-diffusive convection radiation interaction on unsteady MHD flow over a vertical moving porous plate with heat generation and Soret effects.
Shanker et al. [10] were presented a numerical solution for radiation and mass transfer effects on unsteady MHD free convective fluid flow embedded in a porous medium with heat generation/absorption using Galerkinfinite element method. Kumar and Sivaraj [11] studied MHD Visco-elastic fluid non-Darcy flow along a moving vertical cone. Vidyasagar and Raman [12] reported a study on the radiation effect on MHD convection flow of Kuvshinshiki fluid with mass transfer past a vertical porous plate through porous medium. Bhikshu [13] investigated peristaltic flow of a conducting Williamson fluid in a vertical asymmetric channel with heat transfer through porous medium. Devika [14] investigated MHD oscillatory flow of a visco-elastic fluid in a porous channel with chemical reaction. Bhikshu [15] studied the effects of magnetohydrodynamics on the peristaltic flow of fourth grade fluid in an inclined channel with permeable walls. Sivaraj and Kumar [16] were studied an unsteady MHD dusty visco-elastic fluid Couette flow in an irregular channel with varying mass diffusion. Authors are discussed in many chemical engineering processes; the chemical reaction does occur between mass and fluid in which plate is moving [17-20].
These processes occur in varied industrial applications like compound production, producing of ceramics or glasswork and food process. The aim of this work is to investigate the influence of radiation and chemical on MHD convective heat and mass transfer flow of viscous, in-compressible, electrically conducting elastic fluid through porous medium delimited by a porous plate within the presence of heat generation and absorption. Regular perturbation method is adopted to solve governing equations are solved by the perturbation technique [21,22].
Mathematical Formulation of the Problem
We think about two-dimensional unsteady convective flow of Viscous-elastic fluid (Kuvshinski fluid), electrically conducting, an incompressible, past a semi-infinite vertical periodical porous plate in the presence of magnetic field, chemical reaction, heat generation and radiation absorption. Let x* -axis is taken along the porous plate in the rising direction and y* -axis is standard to it. It is assumed that there is no applied voltage of which implies the absence of an electric field. The squarely applied magnetic field and magnetic Reynolds number are very small and hence the made magnetic field is very small. The MHD term is defined from an order of magnitude analysis of the Naiver-stokes equation. We take the porous medium as a collection of minor identical spherical particles fixed in space. The chemical reactions are occurring in the flow and physical properties are taken constant. The magnetic and viscous dissipations are very small. Due to the assumption that the plate in x* -direction is of unlimited length, all the flow variables except pressure are functions of x* and t* only.
The governing boundary layer equation of the flow field considering the above assumptions are given by:
 (1)
(1)
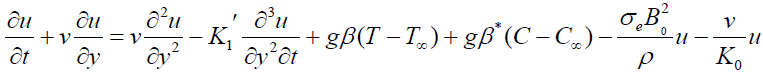 (2)
(2)
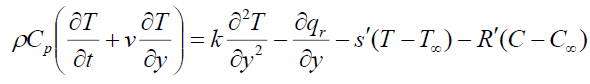 (3)
(3)
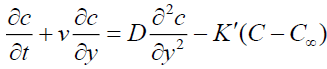 (4)
(4)
Where u,v are the velocity components in x, y directions respectively, t -the time, ρ-the fluid density , v -the kinematic viscosity, Cp -the specific heat at constant pressure, g -the acceleration due to gravity, β and β*-the thermal and concentration expansion coefficient, respectively, B0-the magnetic induction, D-Coefficient of chemical molecular diffusivity, K1 -Reaction rate constant, R1 -Radiation absorption coefficient, s1 -Heat source/sink constant, K -Thermal conductivity, K0 -Permeability of the porous medium, 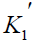 -the dimensional visco-elastic parameter, T -the dimensional temperature,C -the dimensional concentration.
-the dimensional visco-elastic parameter, T -the dimensional temperature,C -the dimensional concentration.
Here the boundary conditions are:
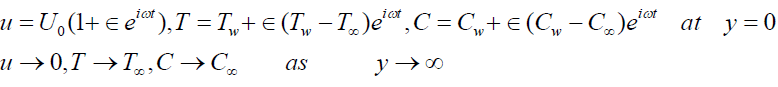 (5)
(5)
Where U0 is the plate velocity, TW and CW are the wall dimensional temperature and concentration, respectively, T∝ and C∝ are the free stream dimensional temperature and concentration, respectively, ω -the constant. From equation (1) we get,
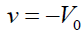 (6)
(6)
Where V0 is the suction velocity normal to the plate.
Introducing the following non-dimensional quantities:
 (7)
(7)
Using the above non-dimensionless quantities and equation (6) the equations (2)-(4) will become,
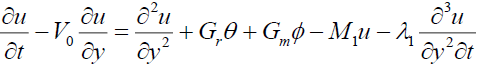 (8)
(8)
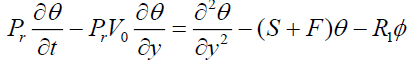 (9)
(9)
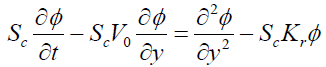 (10)
(10)
Where 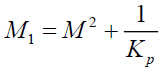
The corresponding boundary conditions are,
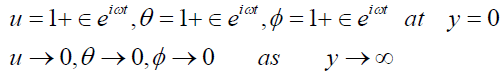 (11)
(11)
Solution of the Problem
The equations 8-10 with boundary conditions (11) are solved, by using the perturbation technique. Let the velocity, temperature and concentration fields as:
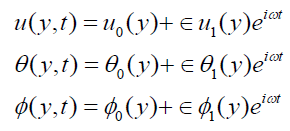 (12)
(12)
Where ∈ is a small quantity 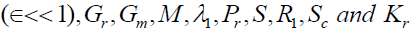 are the thermal Grash of number, Solutal Grashof number, Magnetic parameter, viscoelastic parameter, Prandtl number, heat absorption parameter, radiation absorption parameter, Schmidt number and chemical reaction parameter, respectively.
are the thermal Grash of number, Solutal Grashof number, Magnetic parameter, viscoelastic parameter, Prandtl number, heat absorption parameter, radiation absorption parameter, Schmidt number and chemical reaction parameter, respectively.
Substituting equation (12) into the equations (8)-(10) and equating the like terms, neglecting the terms of ∈2 , then we get,
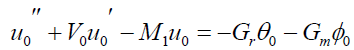 (13)
(13)
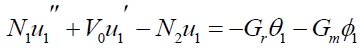 (14)
(14)
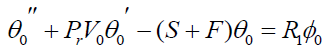 (15)
(15)
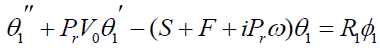 (16)
(16)
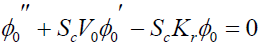 (17)
(17)
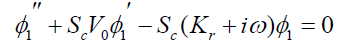 (18)
(18)
Where 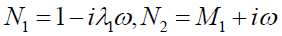
Here the primes denote the differentiation with respect to y.
The boundary conditions are:
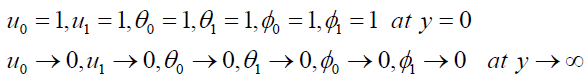 (19)
(19)
In view of (19), solving the equation (13) – (18)
We obtain,
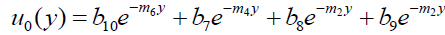 (20)
(20)
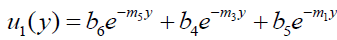 (21)
(21)
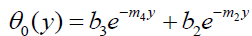 (22)
(22)
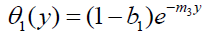 (23)
(23)
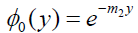 (24)
(24)
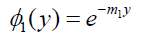 (25)
(25)
On substituting the expressions of 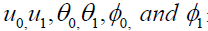 in the equations (12) the
in the equations (12) the
expressions for velocity, temperature and concentration are:
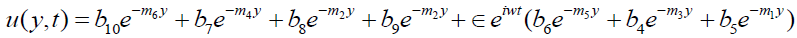 (26)
(26)
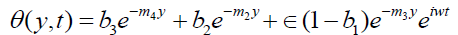 (27)
(27)
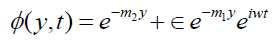 (28)
(28)
Skin-friction at the plate in dimensionless form is given by:
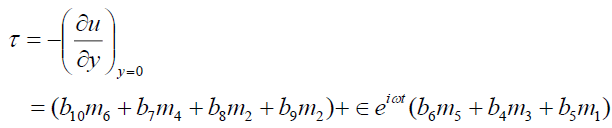 (29)
(29)
Nusselt number
Knowing the rate of heat transfer on the well in terms of Nusselt number Nu is given by:
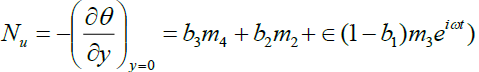 (30)
(30)
Sherwood number
Knowing the rate of mass transfer on the wall is given by:
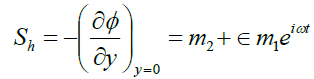 (31)
(31)
Result and Discussion
The physical characteristic of the problem is obtained for the above physical quantities by computing numerically for different values of the governing parameters viz. the Grashof number (Gr), Modified Grashof number (Gm), Prandtl number (Pr), Schmidt number (Sc), magnetic parameter, Permeability parameter (K), Eckert number (Ec) and Heat absorption parameter (Q), heat source parameter (S) radiation parameter (F) and chemical reaction parameter (Kr).
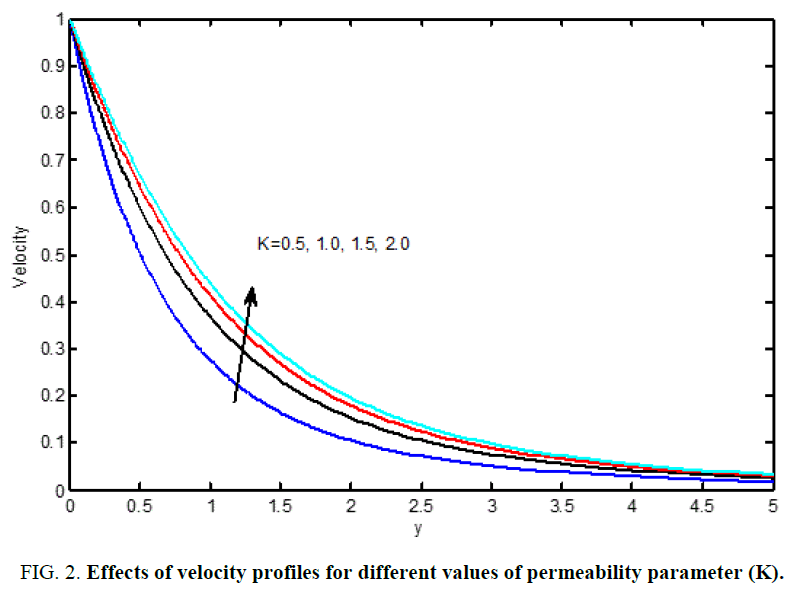
Figure 1 shows the impact of field on magnetic profiles within the boundary layer. Here we have an observed to determined that the velocity profiles are decreases with increasing the magnetic parameter (M). The transverse magnetic field opposes the motion of the fluid and the velocity of transport is significantly reduced. It’s due to with the increase within the magnetic parameter (M), force will increase and it produces a lot of resistance to the flow. Because it will increase, the thermal boundary layer thickness will increase however the momentum boundary layers get belittled. The contribution of the porosity parameter of the fluid bed on the speed field is illustrated in Figure 2. In general, it's noticed that, because the porousness will increase, the speed profiles is additionally will increase for different parameters area unit mounted constants.
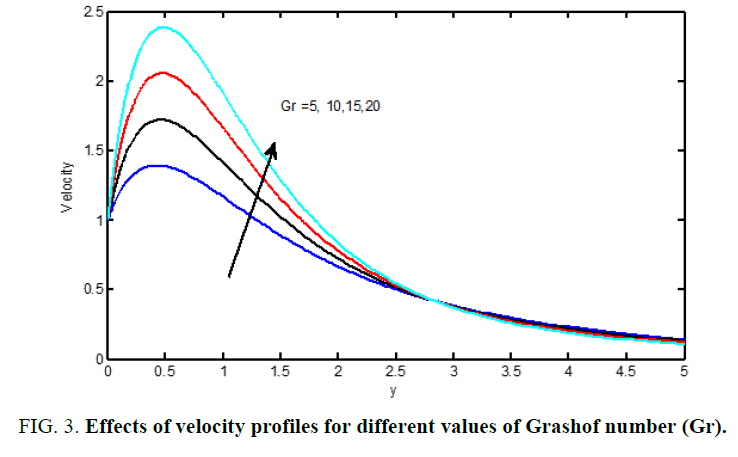
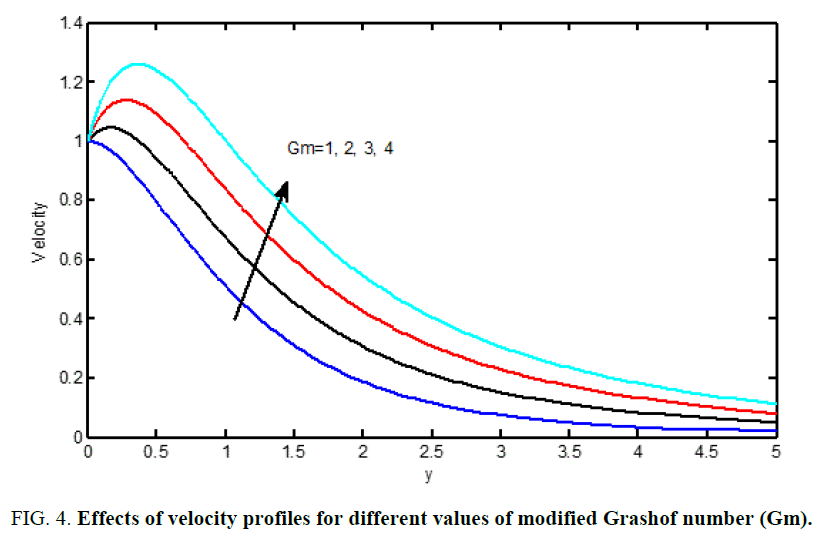
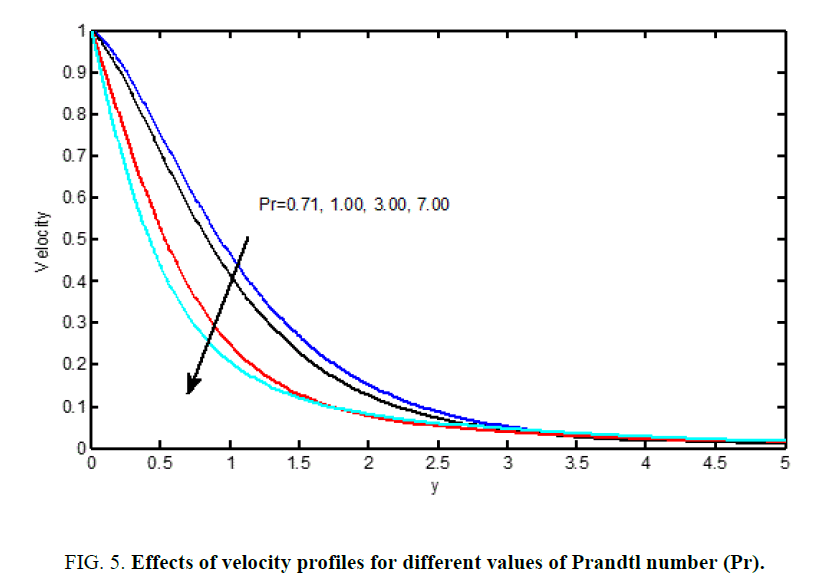
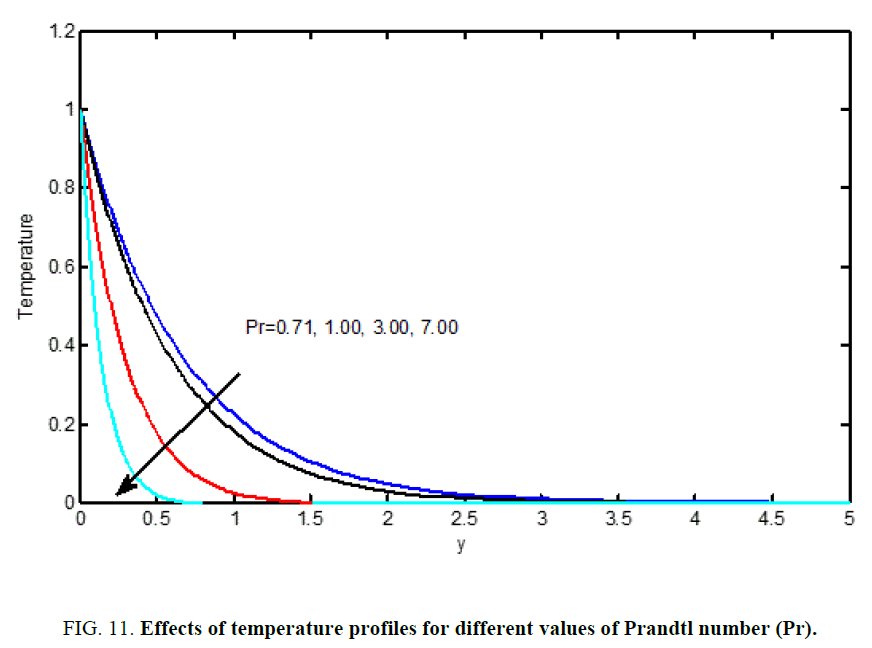
Figure 3 shows that the impact of solutal Grashof range (Gm) on velocity profiles. It's detected that the dimensionless velocity will increase with associate degree increasing the Grashof range. Figure 4 illustrates distinct velocity profiles within the boundary layer for numerous values of solutal Grashof range (Gm). The solutal Grashof range (Gm) defines the quantitative relation of the species buoyancy force to the viscous hydro dynamic force. It’s detected that the velocity will increase with associate degree increasing values of the solutal Grashof range. Additionally, it's found that an increase in metric weight unit ends up in acceleration within the velocity profiles. Figures 5 to 11 illustrate velocity and temperature profiles for various values of Prandtl range (Pr). The numerical results show that the impact of increase values of Prandtl range leads to a decreasing velocity. From Figures 11 to 14, it's detected that an increase within the Prandtl range results a decrease of the thermal physical boundary layer and normally lower average temperature among boundary layer. In the case of smaller Prandtl numbers as the boundary layer is thicker and the rate of heat transfer reduced.
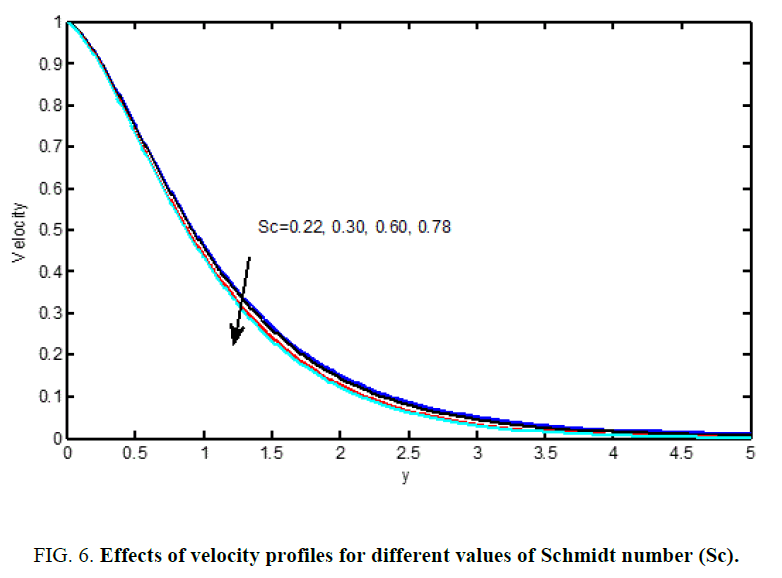
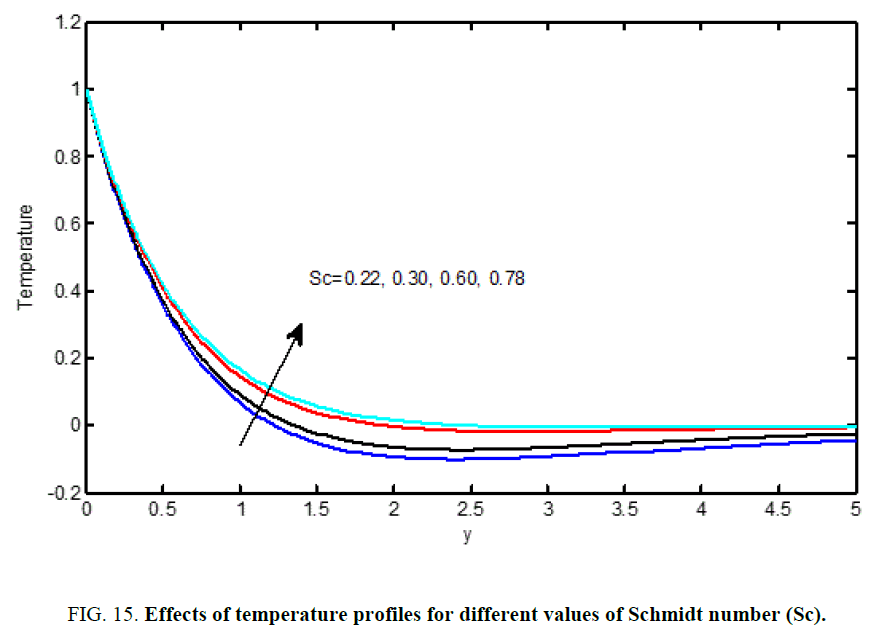
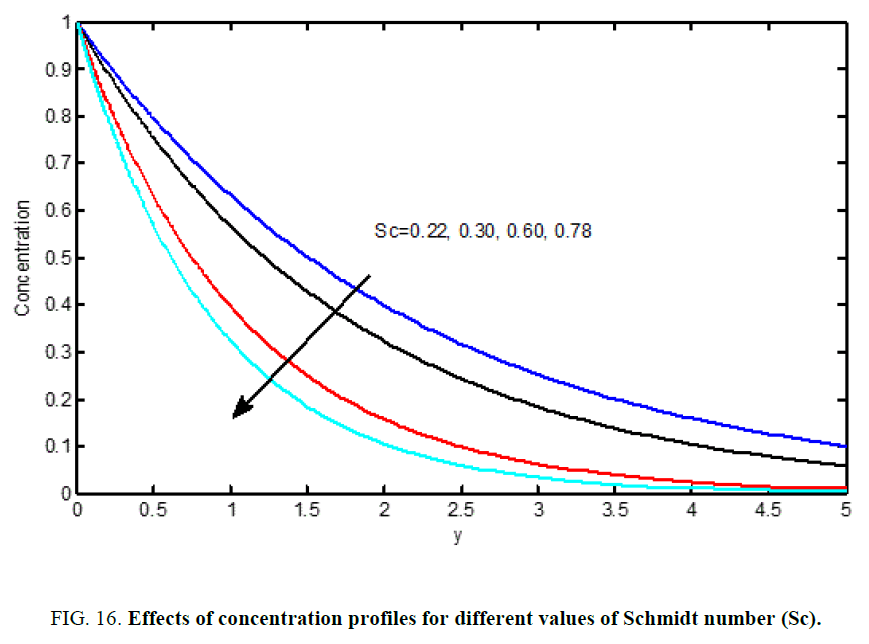
From Figure 6 and Figure 15 we observe that for different values of the Schmidt number (Sc), the velocity and concentration profiles are plotted and that the reductions in the velocity and concentration profiles are accompanied by simultaneous reductions in the velocity and concentration boundary layers, which is evident.
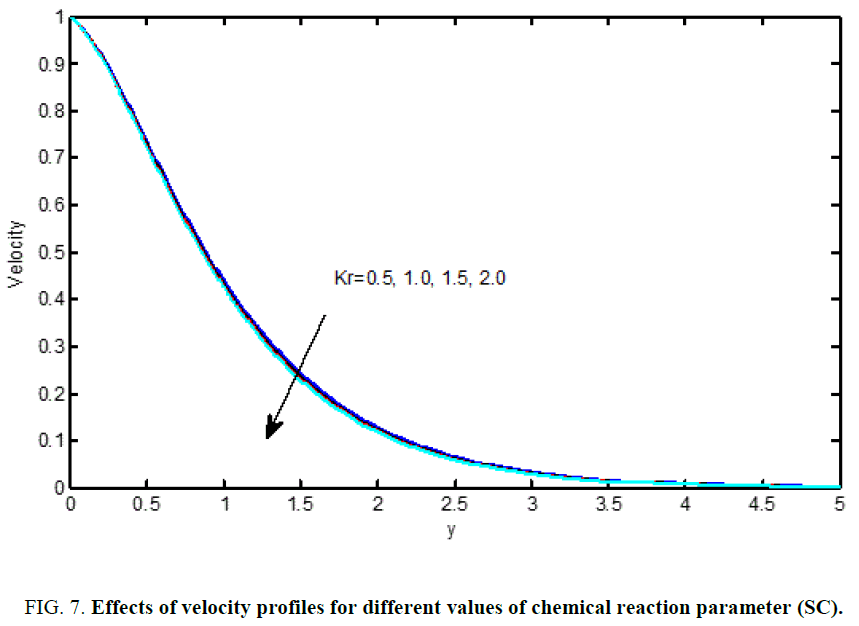
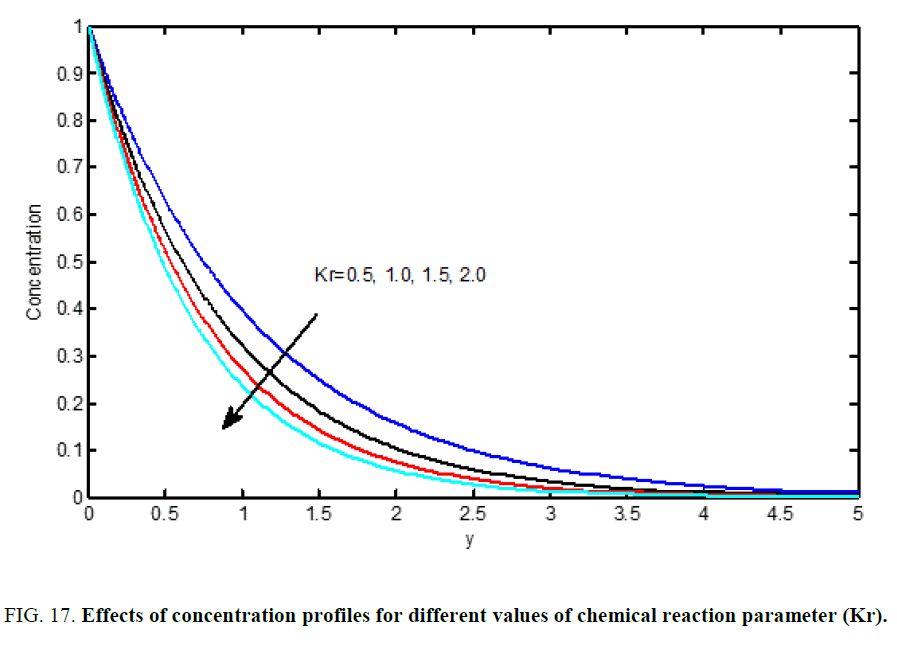
Figure 7 and Figure 16 are shows that the effects of the chemical reaction (Kr) on the velocity and concentration profiles, respectively. It is noticed that as chemical reaction increases, the considerable reduction in the velocity profiles and the presence of the peak indicates that the maximum value of the velocity occurs in the body of the fluid close to the surface but not at the surface. Also, with an increase in the chemical reaction parameter, the concentration decreases. It is evident that the increase in the chemical reaction (Kr) significantly alters the concentration boundary layer thickness but does not alter the momentum boundary layers.
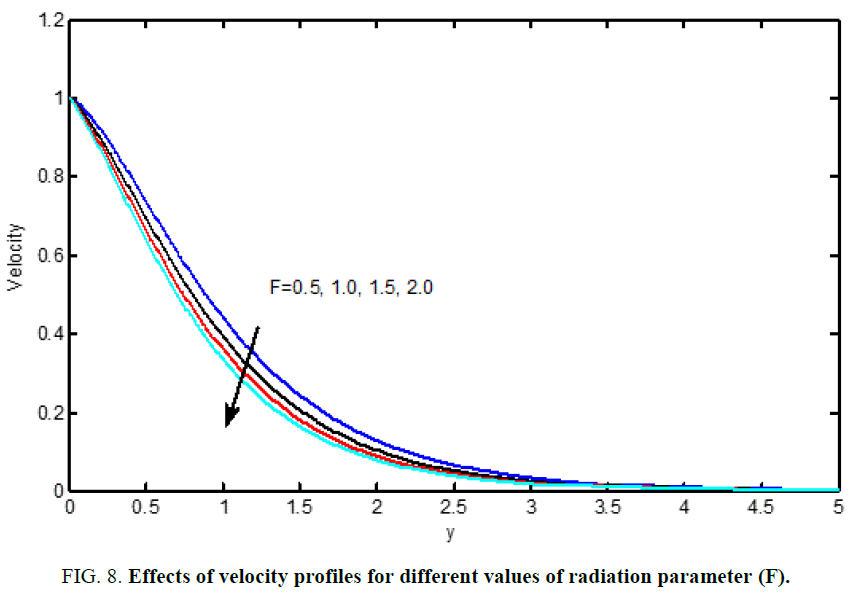
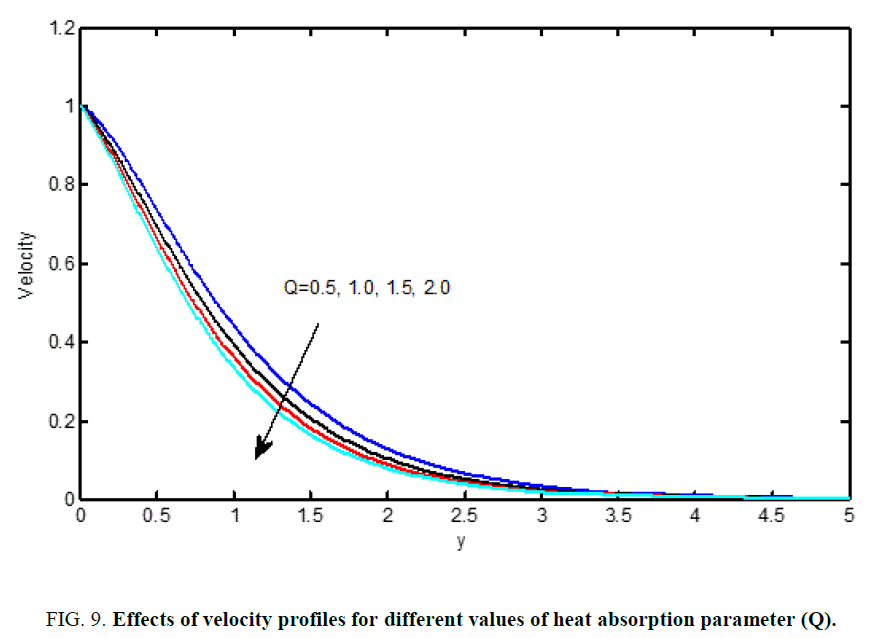
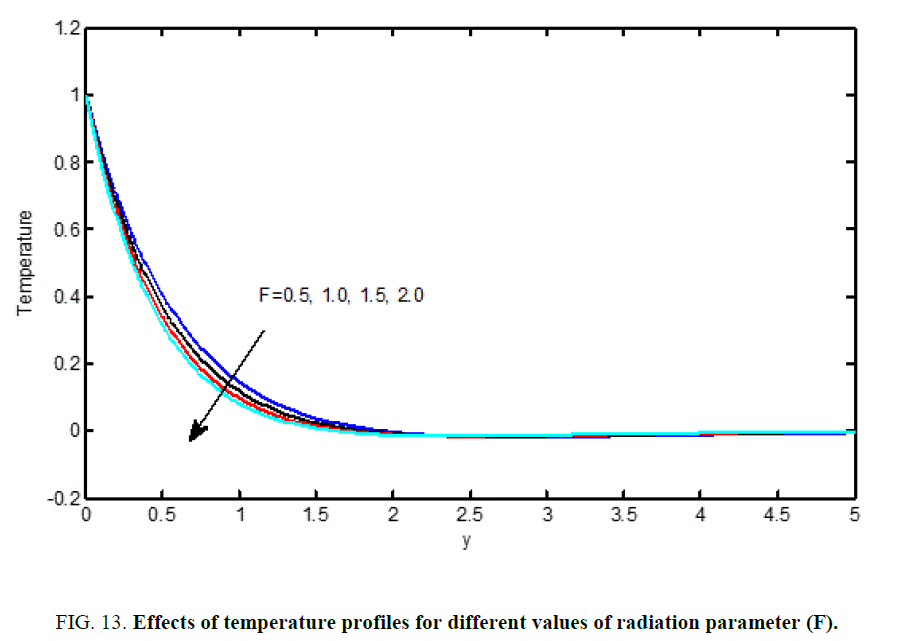
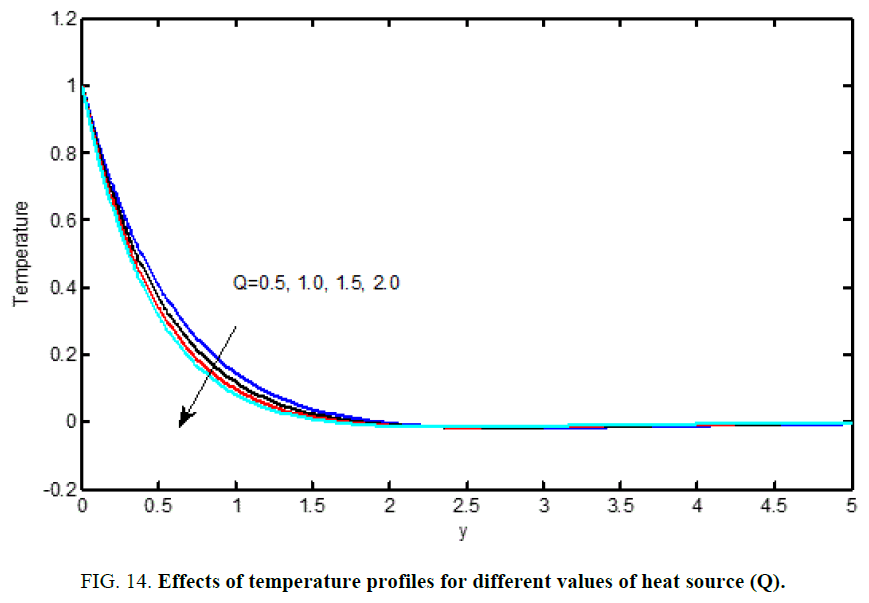
Figure 8 and Figure 13 are shows that the influence of the thermal radiation parameter (F) on the velocity and temperature (Figures 10 and 11). It is observed that an increase in the radiation parameter results in decreasing velocity and temperature within the boundary layer. The effect of increasing the value of the Heat absorption parameter (Q) is to decrease the boundary layer as shown in Figure 9 and Figure 14, which is as expected since when heat is, absorbed the buoyancy force decreases which retard the flow rate and thereby giving rise to decrease in the velocity profiles.
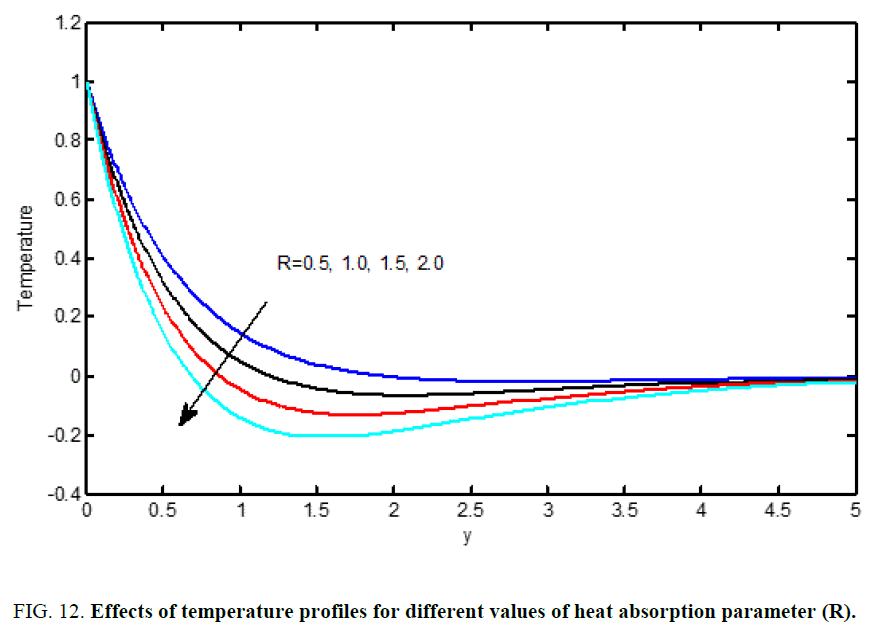
Figure 12 has been plotted to depict the variation of temperature profiles against for different values of heat source parameter (R) by fixing other physical parameters (Figures 13-17). From this graph, we observe that temperature decrease with increase in the Heat source parameter (R).
FIG. 17. Effects of concentration profiles for different values of chemical reaction parameter (Kr).
Conclusion
In this study, an analytical solution of unsteady hydromagnetic free convective heat and mass transfer flow of viscous, in-compressible, electrically conducting viscoelastic fluid through porous medium bounded by porous plate in the presence of chemical reaction, radiation absorption and heat source has been investigated.
The conclusions of the study are follows:
(i) The Hartmann number has the effect of decreasing the flow field both primary and secondary velocity at all the points due to the magnetic pull of the Lorentz force acting on the flow field. So, magnetic field can effectively be used to control the flow.
(ii) The primary and secondary velocity along main flow increase with increasing thermal Grash of number.
(iii) There is an accelerating effect of Sc on the primary and the secondary velocity in presence of heavier diffusing species.
(iv) The chemical reaction parameter has the effect of decreasing the both primary and secondary velocity profiles.
(v) The Prandtl number has a retarding effect on the primary and secondary velocity of the flow field.
(vi) The primary velocity decreases with an increase in heat source parameter and radiation absorption parameter, whereas secondary velocity increases with an increase in heat source parameter and radiation absorption parameter.
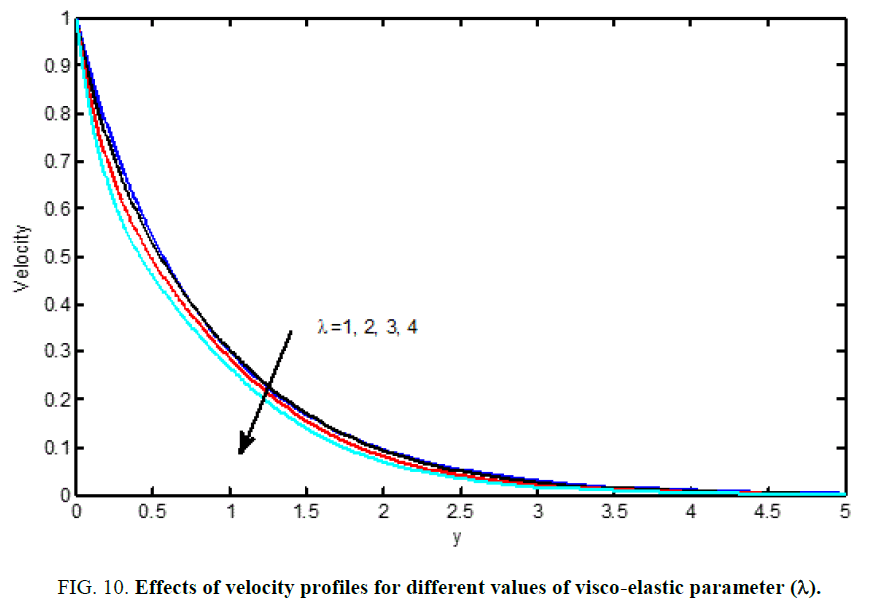
(vii) The viscoelastic parameter has the influence of decreasing the primary and secondary velocity.
References
- Beard DW, Walters K. Elastico-viscous boundary layer flow, I. Two dimensional flows near a stagnation point. Proc Camb Phil Soc. 1964;60:667-4.
- Rajagopal KR. On stokes problem for a non-Newtonian. Fluid Acta Mech. 1983;48:233-9.
- Ibrahim FS, Elaiw AM, Bakr AA. Effect of the chemical reaction and radiation absorption on the unsteady MHD free convection flow past a semi-infinite vertical permeable moving plate with heat source and suction. Communications in Non-linear Science and Numerical Simulation. 2008;13:1056-66.
- Muthucumaraswamy R, Ganesan P. Effect of the chemical reaction and injection on flow characteristics in an unsteady upward motion of an isothermal plate. J Appl Mech Tech Phys. 2001;42:665-71.
- Chamkha J. MHD flow of a numerical of uniformly stretched vertical permeable surface in the presence of heat generation/absorption and a chemical reaction. Int Comm Heat Mass Transfer. 2003;30:413-22.
- Ali Chamkha J. Unsteady MHD convective heat and mass transfer past a semi-infinite vertical permeable moving plate with heat absorption. Int J Eng Sci. 2004;42:217-30.
- Hossain MA, Molla MM, Yaa LS. Natural convection flow along a vertical wavy surface temperature in the presence of heat generation/absorption. Int J Thermal Sci. 2004;43:157-63.
- Hady FM, Mohamed RA, Mahdy A. MHD free convection flow along a vertical wavy surface with heat generation or absorption effect. Int Comm Heat Mass Transfer. 2006;33:1253-63.
- Mohamed RA. Double-diffusive convection radiation interaction on unsteady MHD flow over a vertical moving porous plate with heat generation and soret effects. Appl Math Sci. 2009;3:629-51.
- Shanker B, Prabhakar Reddy B, Ananda Rao J. Radiation and mass transfer effects on unsteady MHD free convection fluid flow embedded in a porous medium with heat generation/absorption. Indian J Pure Appl Phys. 2010;48:157-67.
- Sivaraj R, Rushi Kumar B. Unsteady MHD dusty viscoelastic fluid couette flow in an irregular channel with varying mass diffusion. Int J Heat Mass Transfer. 2012;55:3076-89.
- Vidyasagar G, Raman B. Radiation effect on MHD convection flow of Kuvshinshiki fluid with mass transfer past a vertical porous plate through porous medium. Asian J Curr Engg Maths. 2013;2:170-4.
- Bhikshu NL, Ramana Murthy MV, Ravi Kumar YVK. Peristaltic flow of a conducting Williamson fluid in a vertical asymmetric channel with heat transfer through porous medium. IPASJ International Journal of Mechanical Engineering. 2015;3:27-38.
- Devika B, Satyanarayana PV, Venkataramana S. MHD oscillatory flow of a viscoelastic fluid in a porous channel with chemical reaction. Int J Engg Sci Invention. 2013;2:26-35.
- Bhikshu NL, Ramana Murthy MV, Ravi Kumar YVK. The effects of Magnetohydrodynamics on the peristaltic flow of fourth grade fluid in an inclined channel with permeable walls. Journal of Chemical, Biological and Physical Sciences. 2015;5:4251-68.
- Rushi Kumar B, Sivaraj R. MHD viscoelastic fluid non-Darcy flow along a moving vertical cone. Int J Appl Math Mech. 2012;8:69-81.
- Kishore PM, Rajesh V, Varma SVK. Visco-elastic buoyancy driven MHD free convective heat and mass transfer past a vertical cone with thermal radiation and viscous dissipation effects. Int J Appl Math Mech. 2010;6:67-87.
- Nandeppanavar MM, Abel MS, Tawade J. Heat transfers in a Walter’s liquid-B fluid over an impermeable stretching sheet with non-uniform heat source/sink and elastic deformation nonlinear. Sci Numer Simulat. 2010;15:1791-1802.
- Mohiddin SG, Prasad VR, Varma SVK, et al. Numerical study of unsteady free convective heat and mass transfer in a Walters-B viscoelastic flow along a vertical cone. Int J Appl Math Mech. 2010;6:88-114.
- Mahantesh MN, Abel MS, Tawade J. Heat transfer in a Walter’s liquid-B Fluid over an impermeable stretching sheet with non-uniform heat source/sink and elastic deformation. Commun Nonlinear Sci Numer Simulat. 2010;15:1791-1802.
- Chang T, Mehmood A, Beg OA, et al. Numerical study of transient free convective mass transfer in a Walters-B viscoelastic flow with wall suction. Commun Nonlinear Sci Numer Simulat. 2011;16:216-225.
- Balamurugan KS, Ramaiah P, Varma SVK, et al. Thermal radiation and radiation absorption effects on unsteady MHD double diffusive free convection flow of Kuvshinski fluid past a moving porous plate embedded in a porous medium with chemical reaction and heat generation. Far East J Math Sci. 2014;91:211-231.