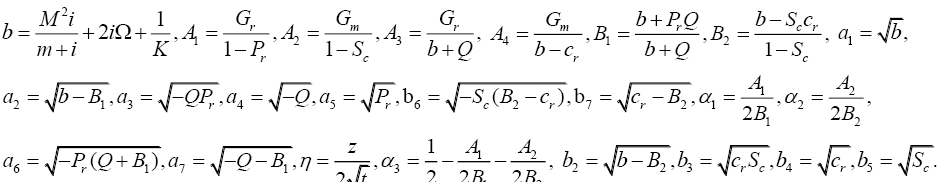Original Article
, Volume: 15( 3)Unsteady MHD Flow Past Impulsively Started Vertical Plate in Porous Medium with Heat Source and Chemical Reaction
- *Correspondence:
- Shareef M, Department of Mathematics and Astronomy, University of Lucknow, Lucknow, India, Tel: +91-9307525914; E-mail: rajputshareeflu@gmail.com
Received: May 10, 2017; Accepted: June 28, 2017; Published: July 03, 2017
Citation: Rajput US, Shareef M. Unsteady MHD Flow Past Impulsively Started Vertical Plate in Porous Medium with Heat Source and Chemical Reaction. Int J Chem Sci. 2017;15(3):154
Abstract
An unsteady MHD free convective flow of an incompressible, electrically conducting, viscous fluid along an infinitely long vertical plate with an impulsive motion in the presence of heat source and homogeneous binary chemical reaction in a rotating system is studied here. The dimensionless form of governing equations is obtained and solved analytically with the help of Laplace transform method. The solutions obtained for concentration, temperature and velocity distribution are analyzed graphically. The numerical values of the skin friction at the plate are shown in the table. It is noticed that for a strong magnetic field the flow pattern is affected significantly by Hall current at a different rotation. The results obtained may be useful for applications in the area related to the structure of rotating magnetic stars, the solar physics which deals the sunspot development, and the solar cycle, etc.
Keywords
Radiation; Porous plate; Velocity
Introduction
The convective boundary layer flow along an infinite flat plate is one of the important problems. An impulsive motion of a plate in a viscous fluid was studied by Stewartson [1,2]. His study was completely based within the context of boundary layer equations. If the fluid is electrically conducting then the magnetic field can stabilize such a flow within a porous and non-porous medium. And the magneto hydrodynamic flow with heat generation and chemical reaction is widely used in many engineering processes with applications in industries. In recent years, considerable progress has been made in the study of the thermo physical properties affecting magneto hydrodynamic flow. For instance, the magneto hydrodynamic flow of a vertical permeable uniformly stretched surface with chemical reaction and heat absorption/generation was studied by Chamka [3]. He solved the problem analytically and observed that the Prandlt number, Schmidt number and the strength of magnetic field retard the fluid velocity. Prasad et al. [4] analyzed the 2-D impulsive motion of an infinite vertical plate with mass transfer and radiation. They solved the model by finite-difference method and observed that when the radiation parameter increases, the fluid velocity decreases near the plate. Further, Ibrahim et al. [5] studied the effect of chemical reaction on magneto hydrodynamic flow with mass and heat transfer along a moving vertical porous plate. Further Ibrahim et al. [6] extended their work by considering the radiation on the same model.
Hall current term in generalized Ohm’s law cannot be neglected for the problems having a strong magnetic field. Also, the rotating flow of incompressible, electrically conducting and viscous fluid has abundant geophysical and astrophysical applications. So, many scholars have studied such models, for instance, Agarwal et al. [7] studied the combined effect of Hall current and dissipation on rotating fluid with free convective motion. Seth et al. [8] worked on unsteady hydro magnetic free convective flow along a moving vertical plate with rotation and thermal radiation in porous medium and observed that rotation retards fluid velocity in primary flow direction; whereas it accelerates fluid flow in the secondary flow direction in the boundary layer region. Some other scholars such as Prakash et al. [9], Ramana et al. [10] and Reddy [11] have studied the MHD flow with radiative heat-mass transfer and chemical reaction. The present model analyzes the combined effect of rotation and Hall current on unsteady magneto hydrodynamic convective flow past along impulsively started vertical flat plate with a heat source and chemical reaction in a porous medium.
Mathematical Model
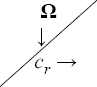
Consider viscous, electrically conducting and incompressible fluid through porous medium. Let x '— axis be chosen vertically upward along the motion of the plate. And the normal direction of the plate is taken along the z'— axis. Also, the plate and the fluid are rotating together as a rigid body about z'— axis with a constant angular velocity Ω' . A constant magnetic field Bo is applied along z'— axis. As the plate is infinitely long lying in the x '— y ' plane; so, various physical variables involved in the problem are considered as the functions of t ' and z ' only.
Initially at a time t ' ≤ 0, the system is at rest; and has a constant temperature and concentration T∞and C∞ respectively. At the time t ' > 0 , the plate starts moving with a constant velocity uo along x '— axis. Also, the concentration and temperature of the plate are raised to Cp and Tp respectively. The impulsive motion of the plate and the free convection causes the disturbance in the fluid. From electric charge conservation equation  we have Jz ' = constant, where
we have Jz ' = constant, where 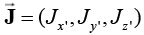 is the current density vector. As the plate is non-conducting, so at the plate . Jz'=0 Thus Jz'=0 everywhere in the fluid. Under the above assumptions, the governing equations with Boussinesq’s approximation are as follows:
is the current density vector. As the plate is non-conducting, so at the plate . Jz'=0 Thus Jz'=0 everywhere in the fluid. Under the above assumptions, the governing equations with Boussinesq’s approximation are as follows:
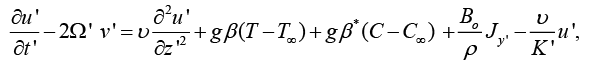 (1)
(1)
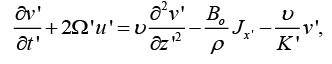 (2)
(2)
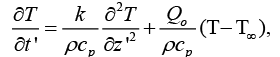 (3)
(3)
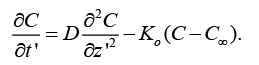 (4)
(4)
The boundary conditions taken are as under:
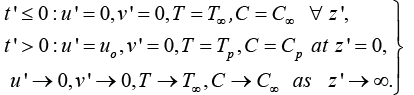 (5)
(5)
Taking Hall current into account and neglecting the electron pressure gradient, the ion slips and the thermo-electric effects, the generalised Ohm’s law is given as:
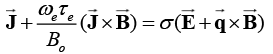 (6)
(6)
On solving (6), we get 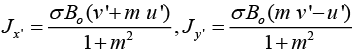
To obtain the equations in non-dimensional form, the following dimensionless parameters are introduced:
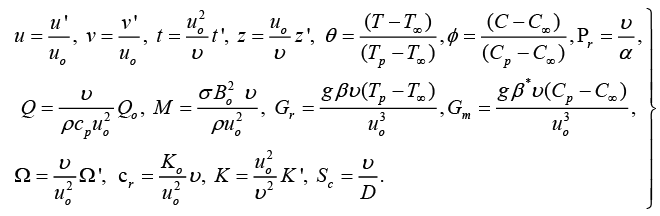 (7)
(7)
Using equation (7), equations (1), (2), (3), (4) and (5) respectively, become:
 (8)
(8)
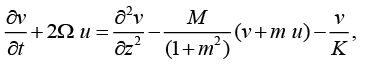 (9)
(9)
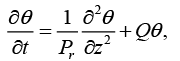 (10)
(10)
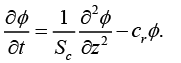 (11)
(11)
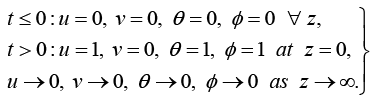 (12)
(12)
To solve above system, assume V= u ?iv . Then using equations (8) and (9), we get,
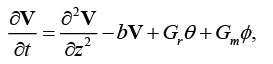 (13)
(13)
The boundary conditions (12) are transformed:
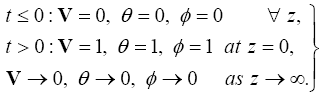 (14)
(14)
The dimensionless PDEs (10), (11) and (13), with the boundary conditions (14) are solved with the help of Laplace transform method 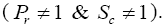
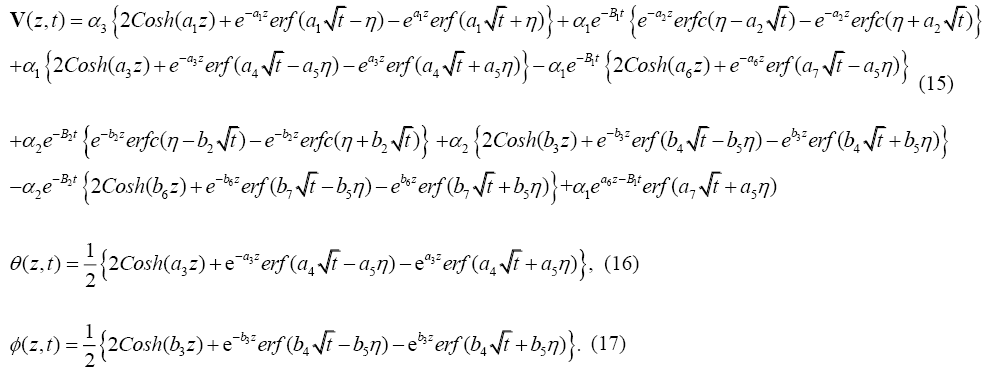
The skin-friction components xτ and yτ are obtained as:
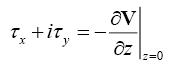
Results and Discussion
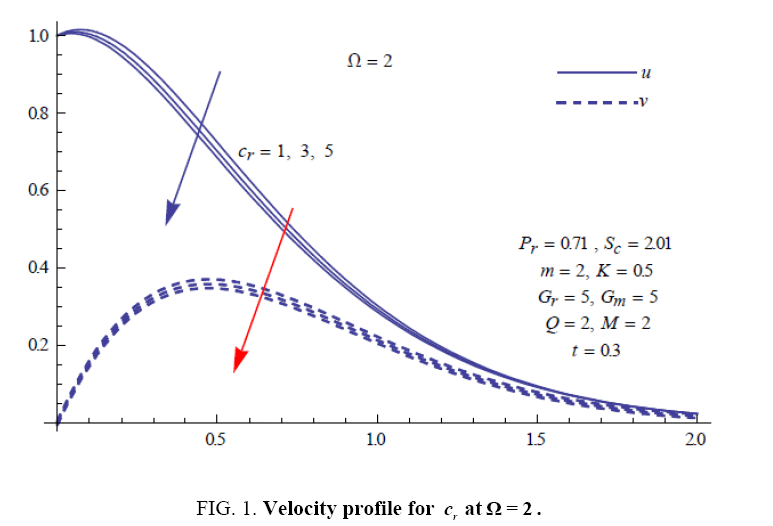
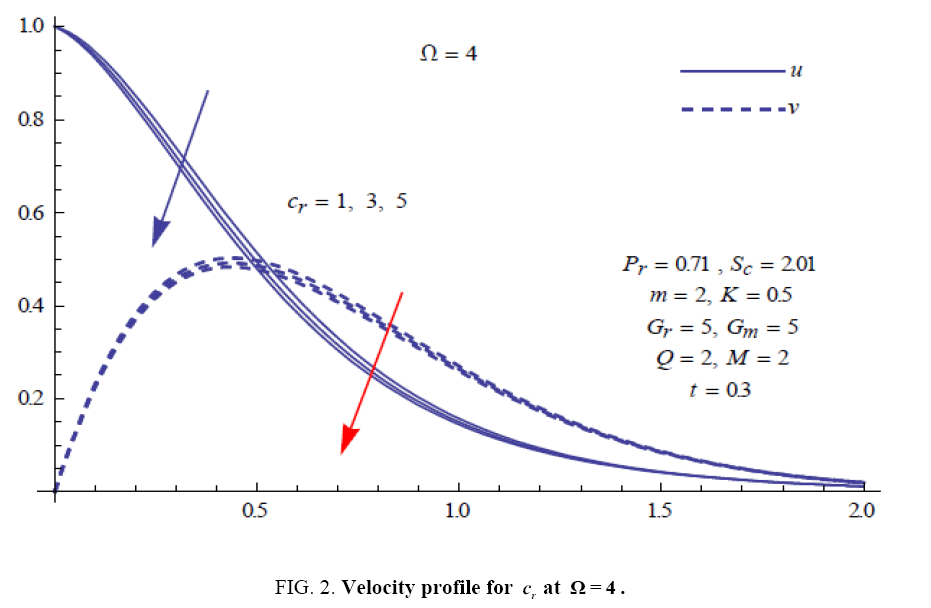
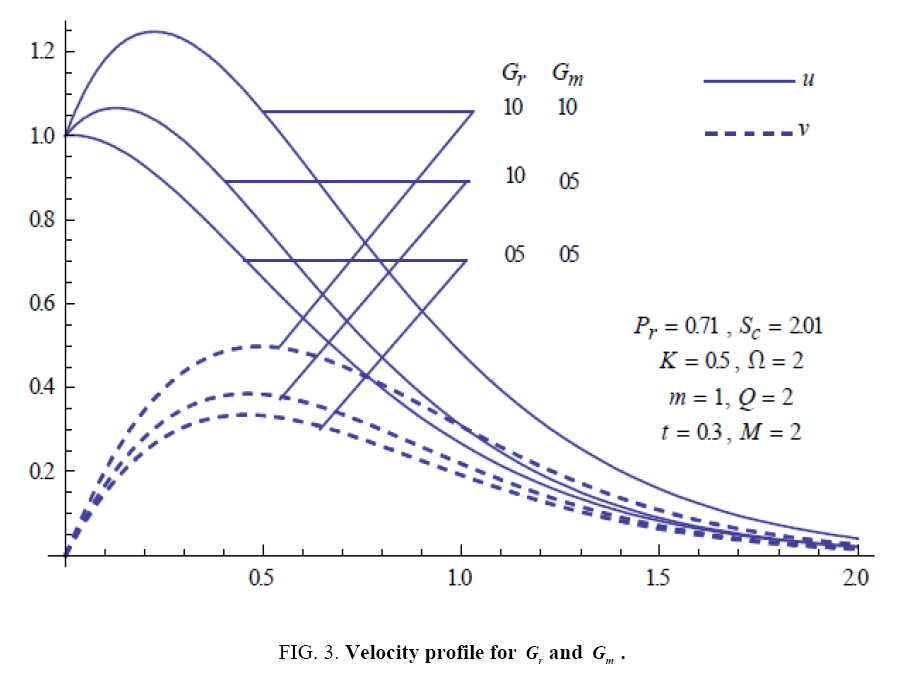
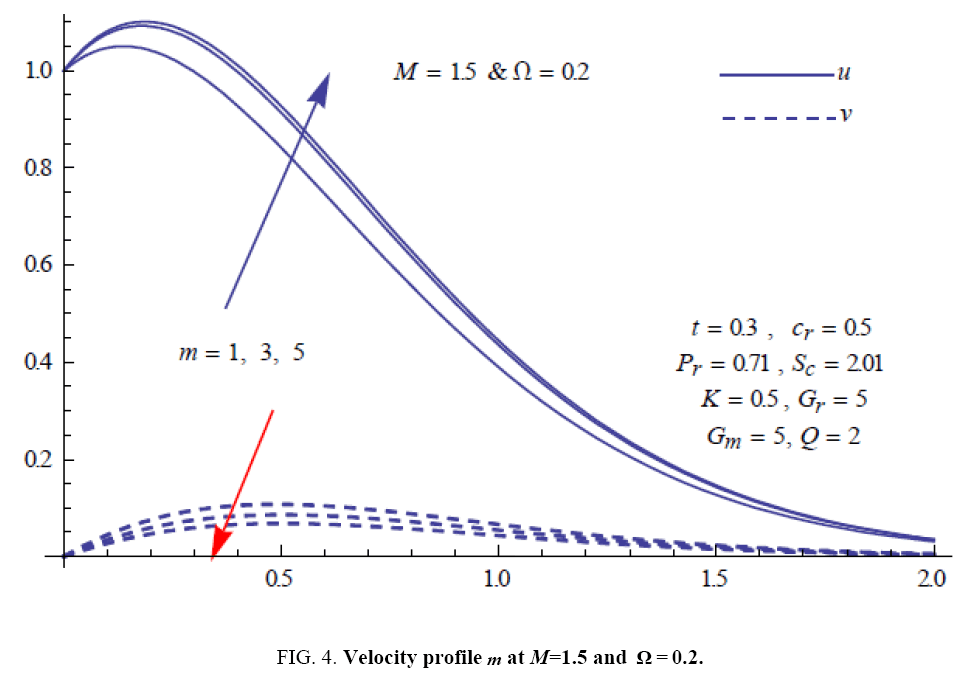
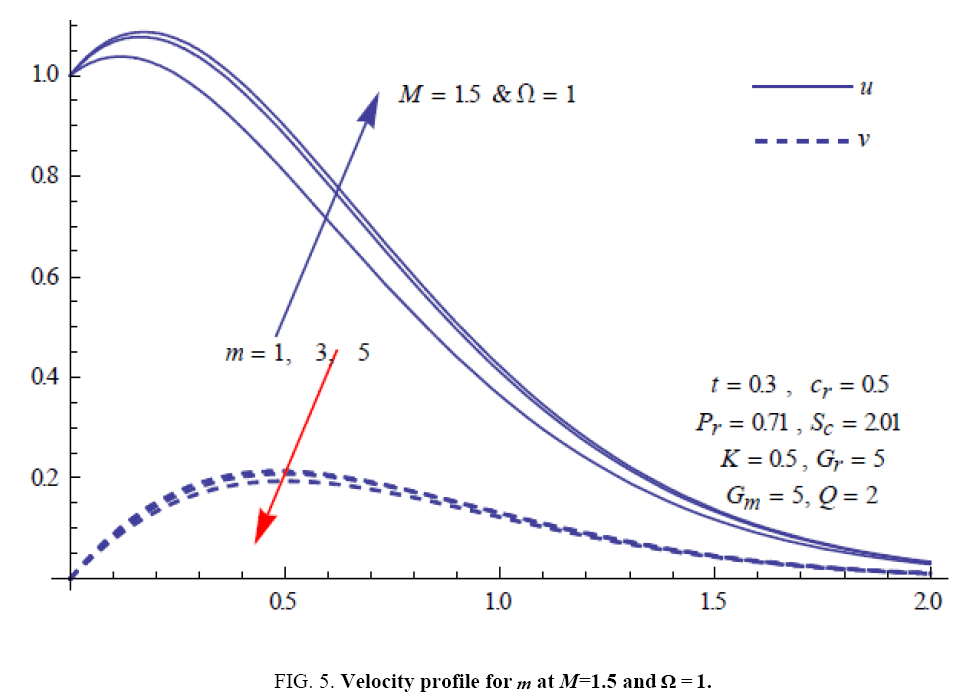
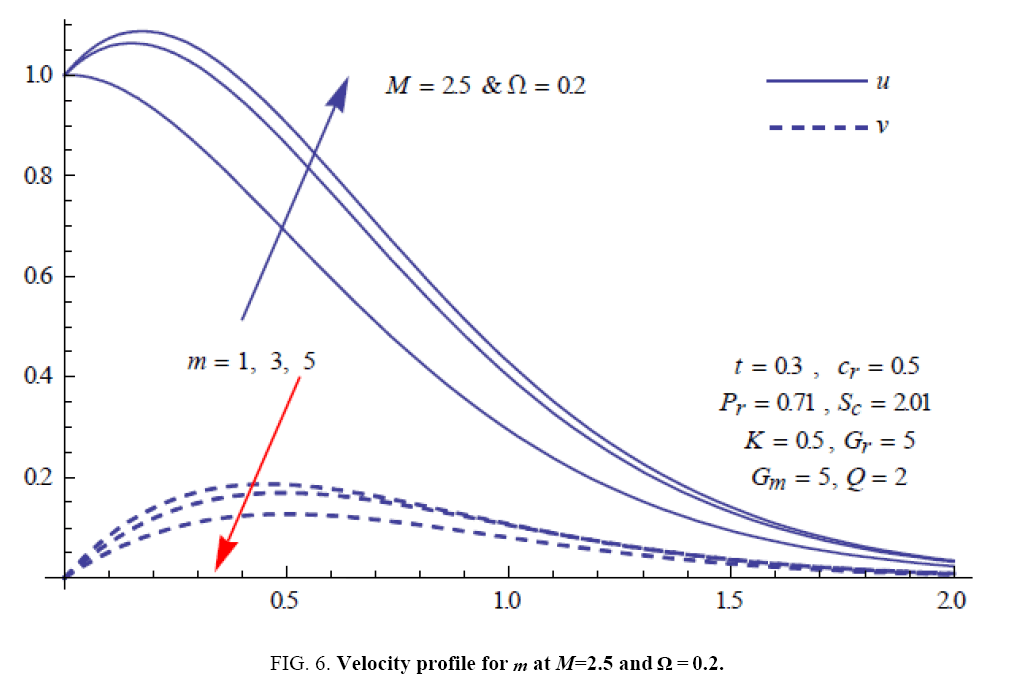
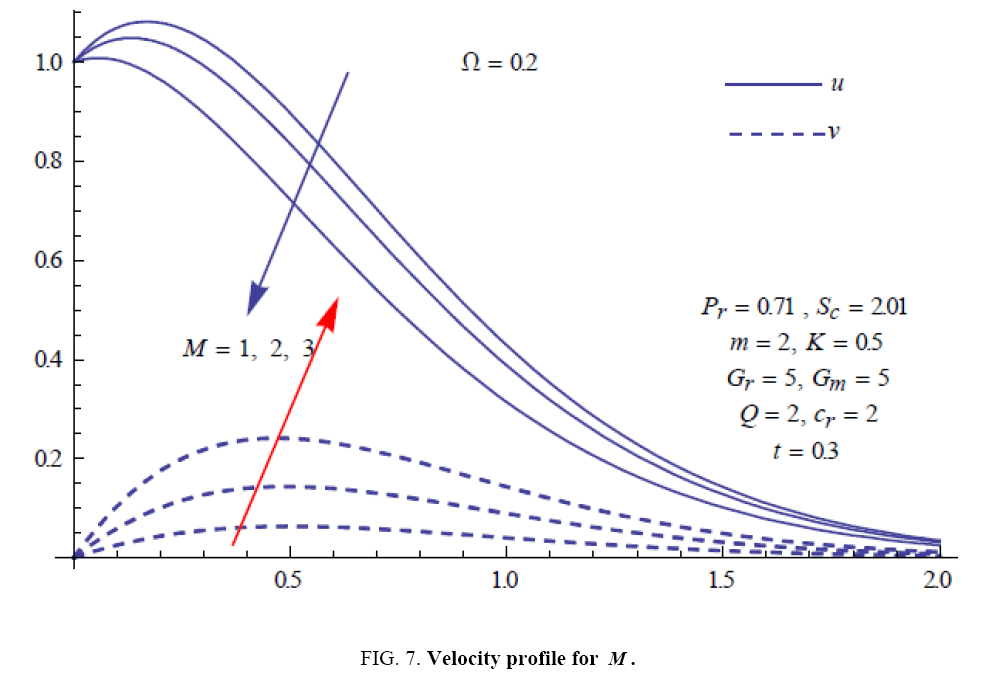
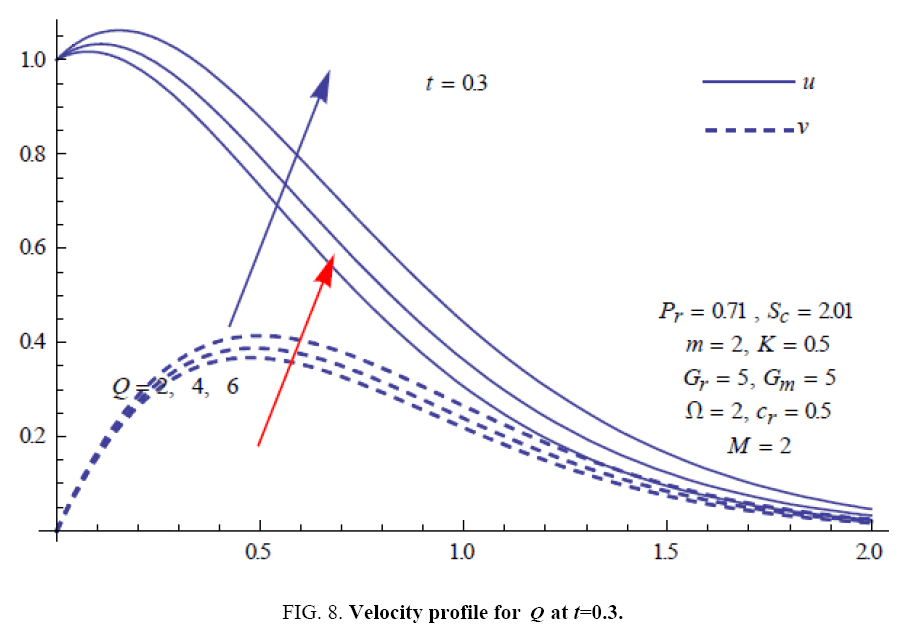
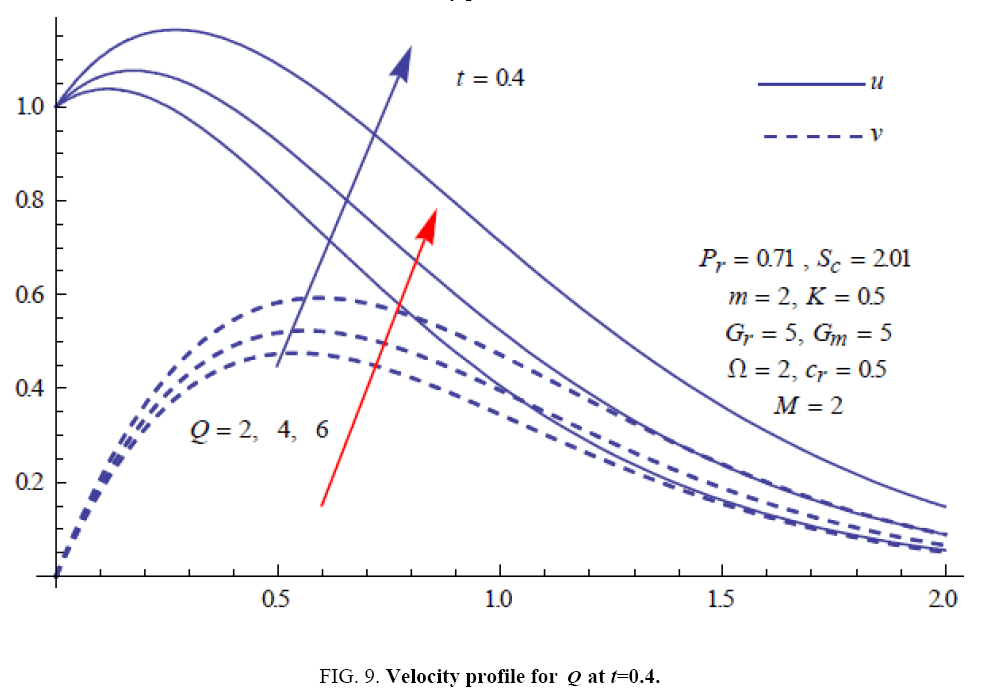
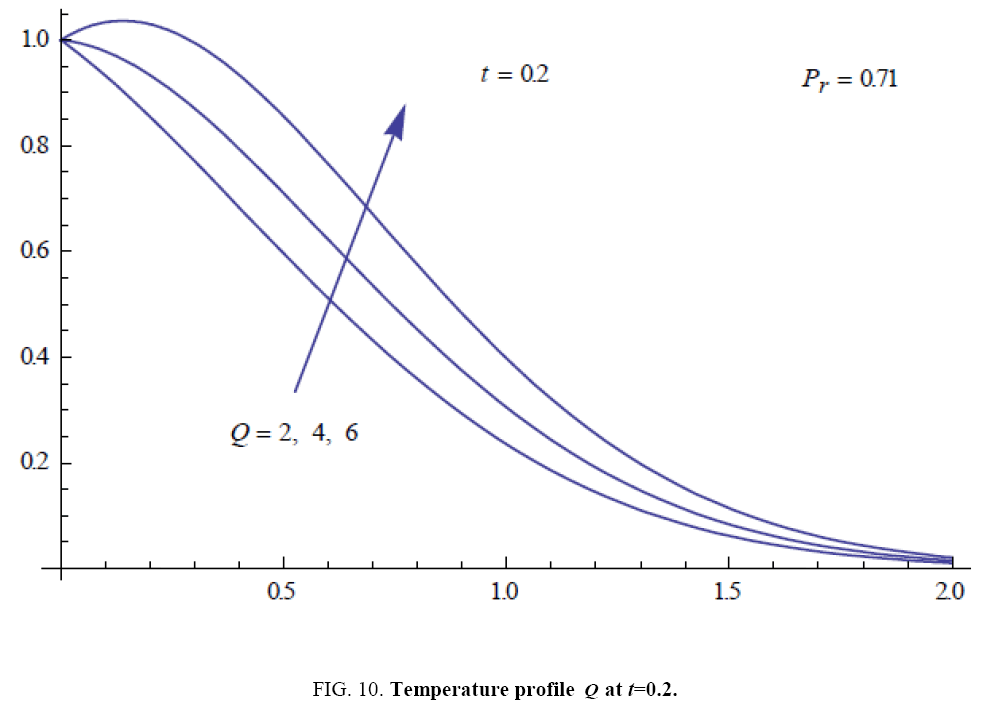
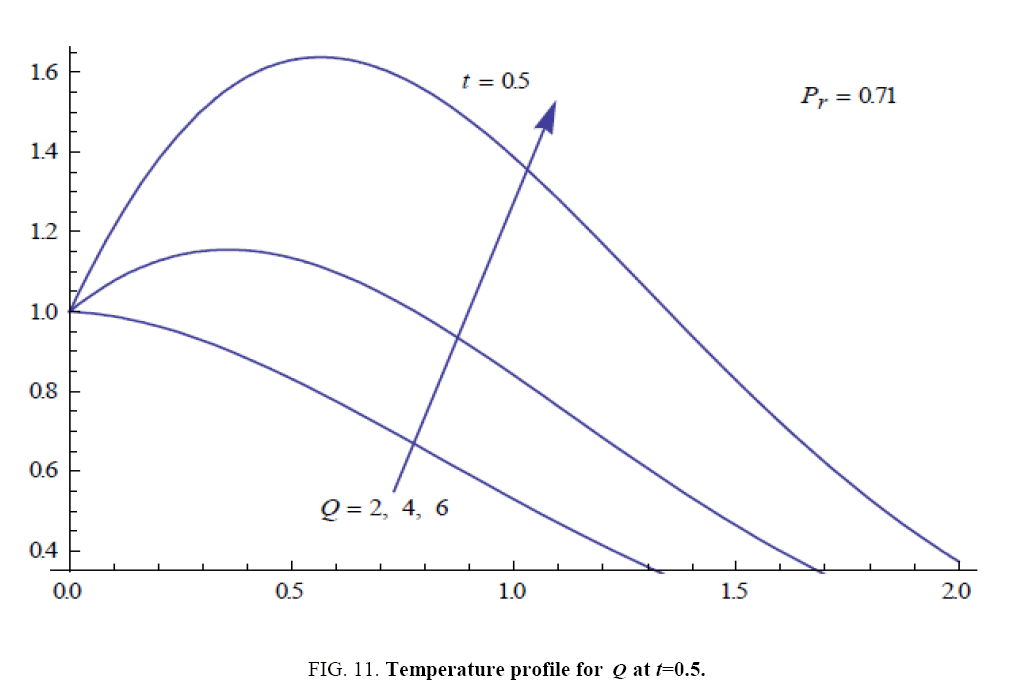
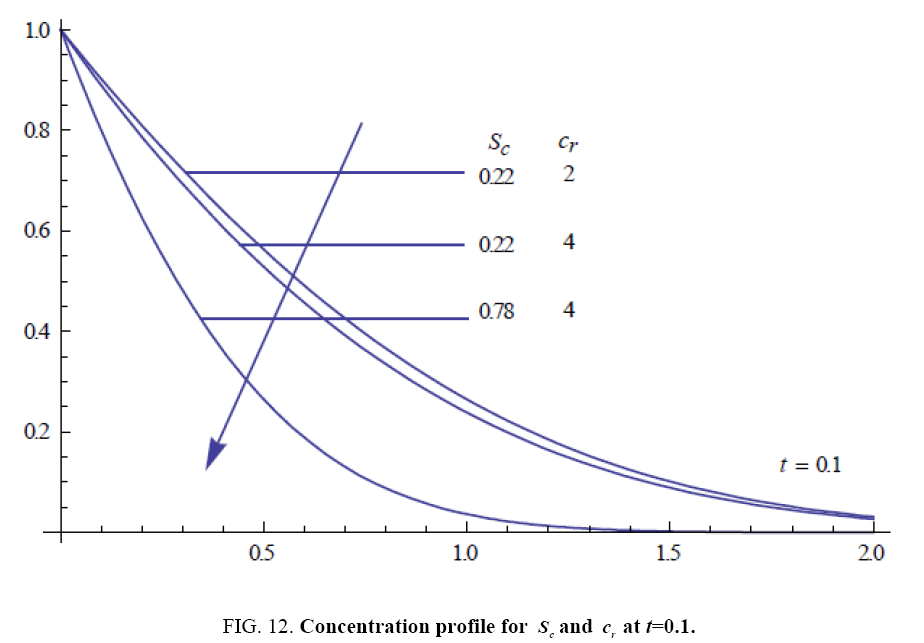
To examine the influence of chemical reaction, magnetic field, heat source, rotation, Hall current and time on flow, a number of selected graphs for velocity versus boundary layer length are shown in Figure 1 to 9. These graphs show that the magnitude of primary velocity u and secondary velocity v decrease rapidly on increasing boundary layer length to approach free stream value. From the Figure 1 and 2, it is observed that with the increase in cr (chemical reaction parameter) both the components of velocity go on decreasing. The rate of decrease becomes sharp with an increase in rotation. Effect of bouncy force can be seen from Figure 3, which shows that the buoyancy force accelerates the flow in both the directions. This is because of an increase in the values of thermal and mass Grashof number. Figure 4, 5 and 6 show the effect of Hall current on the fluid velocity at the different rotation. It is noticed that the velocity of the fluid in the primary direction increases, whereas secondary velocity decreases on increasing Hall current parameter m. This shows that Hall current tends to accelerate fluid flow along the primary direction; whereas it tends to retard secondary velocity throughout the boundary layer region. It can be observed that the Hall current stabilizes the fluid velocity only if the strength of applied magnetic field is strong (Figure 6). Figure 7 shows that the magnetic field parameter retards the flow in the primary direction while accelerates the flow in the secondary direction. It is because of an applied transverse magnetic field which produces a resistive type force known as the Lorentz force. Figure 8 and 9 illustrate the influence of heat source parameter Q at different instant of time. In both the cases, Q accelerates the flow in both the directions. But as the time increases the rate of increase becomes high. Figure 10 and 11 displays the variation of the temperature distribution in the fluid near the plate with heat source parameter at a different time for Pr=0.71 . It is found that at a particular instant of time temperature in the system increases with the increase in the heat source parameter. Figure 12 and 13 depict concentration distribution at different times which shows that an increase in Sc or cr reduces the thickness of the concentration boundary layer. Table 1 display the variation of skin friction due to variation in chemical reaction parameter cr at different rotation. It is found that for a fixed rotation, τx increases with cr , and τy decreases with increase in cr .
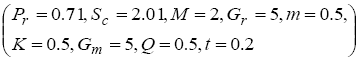
 |
-τx(10-3) | -τy(10-3) | ||||
|---|---|---|---|---|---|---|
| 1 | 3 | 5 | 1 | 3 | 5 | |
| 2 | 1035 | 938 | 862 | 192 | 168 | 149 |
| 4 | 949 | 863 | 795 | 289 | 252 | 222 |
Table: Skin-fiction for cr .
Conclusion
It is found that Hall current has a tendency to accelerate the primary flow while it retards secondary flow. An increase in the chemical reaction parameter corresponds to decrease in both the component of the fluid velocity as well as the concentration in the system. However, the fluid velocity in both the directions as well as the temperature increases with the increase in heat source parameter. Also, the solution (15) obtained is valid only for Pr ≠1 and Sc≠1 . For the case when Pr=1 and Sc=1, the thicknesses of concentration, momentum and thermal boundary layers are of the same order of magnitude. It is also found that τx increases and τy gets decreased with cr .
Symbols
Cp: Specific Heat at Constant Pressure;
Cr: Dimensionless Chemical Reaction
Parameter;
D: Mass Diffusion Coefficient;
g: Acceleration Due to Gravity;
Gm: Mass Grashof Number;
Gr: Thermal Grashof Number;
Ke: Mean Absorption Coefficient;
K´: Permeability Parameter;
m: Hall Parameter;
v´: Secondary Velocity of the Fluid;
v: Dimensionless Secondary Velocity of the Fluid;
Z: Dimensionless Spatial Coordinate Normal to the Plate;
α: Thermal Diffusivity;
β: Volumetric Coefficient of Thermal; Expansion;
β*: Volumetric Coefficient of Concentration; Expansion;
θ:Dimensionless Temperature;
v: Kinematic Viscosity;
ρ: Density of Fluid;
M: Magnetic Field Parameter;
Pr: Prandlt Number;
Qo: Heat Source Coefficient;
Q: Dimensionless Heat Source Coefficient;
Sc: Scthimth Number;
t: Dimensionless Time;
u´: Primary Velocity of the Fluid;
u: Dimensionless Primary Velocity of the Fluid
?s: Stefan-Boltzmann Constant;
τe: Electron Collision Time;
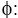 Dimensionless Concentration;
Dimensionless Concentration;
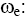 Cyclotron Frequency of Electron;
Cyclotron Frequency of Electron;
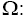 Dimensionless Rotation Parameter;
Dimensionless Rotation Parameter;
References
- Stewartson K. On the impulsive motion of a flat plate in a viscous fluid. Part 1, Quart J MechAppl Math. 1951;4:182-98.
- Stewartson K. On the impulsive motion of a flat plate in a viscous fluid. Part 2, Quart J MechAppl Math. 1973;22:143-52.
- Chamka AJ. MHD flow of a uniformly stretched vertical permeable surface in the presence of heat generation/absorption and chemical reaction. Int Com Heat Mass Transfer. 2003;3:413-22.
- Prasad VR, Bhaskar Reddy N, Muthucumaraswamy R. Radiation and mass transfer effects on two-dimensional flow past an impulsively started infinite vertical plate. Int J Thermal Sci. 2007;46:1251-58.
- Ibrahim SY, Makinde OD. Chemically reacting MHD boundary layer flow of heat and mass transfer over a moving vertical plate with suction. Sci Research & Essays. 2010;5:2875-82.
- Ibrahim SY, Makinde OD. Radiation effect on chemically reacting (MHD) boundary layer flow of heat and mass transfer through a porous vertical flat plate. Int J Phy Sci. 2011;6:1508-16.
- Agarwal HL, Ram PC, Singh V. Combined influence of dissipation and Hall effect on free convective flow in a rotating fluid. Indian J Pure ppl Math. 14:314-32.
- Seth GS, Nandkeolyar R, Ansari MS. Effects of thermal radiation and rotation on unsteady hydro magnetic free convection flow past an impulsively moving vertical plate with ramped temperature in a porous medium. J App Fluid Mech. 2013;6:27-38.
- Prakash J, Vijaya Kumar AG, Madhavi M, et al. Effects of chemical reaction and radiation absorption on MHD Flow of dusty viscoelastic fluid. App and Applied Maths: An Int J (AAM). 2014;9:141-56.
- Reddy RGV, Reddy BN, Chamkha AJ. MHD mixed convection oscillatory flow over a vertical surface in a porous medium with chemical reaction and thermal radiation. J App Fluid Mechanics. 2016;9:1221-9.
- Reddy MG. Heat and mass transfer e?ects on unsteady MHD radiative flow of a chemically reacting fluid past an impulsively started vertical plate. MATEMATIKA. UTM Centre for Industrial and Applied Mathematics. 2014;30:1-15.
Appendix