Original Article

, Volume: 15( 3)

• View PDF
• Download PDF

Total Pathos Edge Semi Entire Block Graph

*Correspondence:

Venkanagouda M Goudar , Department of Mathematics, Sri Siddhartha Institute of Technology, Tumkur, Karnataka, India, Tel: 9448579479; E-mail: vmgouda@gmail.com

Abstract

In this paper, we introduce the concept of total pathos edge semi entire block graph of a tree. We obtain some properties of this graph. We study the characterization of graphs whose total pathos edge semi entire block graphs are always nonplanar, crossing number one, Eulerian and Hamiltonian.

Keywords

Block graph; Edge Semientire graph; Inner vertex number; Line graph

Introduction

Let G (p,q) be a connected graph with vertex set V=p and the edge set E=q. If e=uv is in E (G), then the vertices u and v are adjacent. For the graph theoretical notation, we follow in [1,2].

In [3] Venkanagouda et al. introduced the graph valued function, the pathos edge semi entire block graph of a tree T. The block graph B (G) of a graph G was introduced in [2]. Further the path graph P (T) of a tree was studied in [3].

The following theorems will be used in the sequel.

Theorem 1 [6]. If G is a (p, q) graph whose vertices have degree d_i then L (G) has q vertices and qL edges where

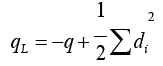
Theorem 2 [6]. The line graph L (G) of a graph G has crossing number one if and only if G is planar and 1 or 2 holds:

1. The maximum degree d (G) is 4 and there is unique non-cut vertex of degree 4.

2. The maximum degree d (G) is 5, every vertex of degree 4 is a cut vertex and there is a unique vertex of degree 5 and has at most 3 edges in any block.

Theorem 3 [2]. A connected graph G is isomorphic to its line graph if and only if it is a cycle [4].

Theorem 4 [6]. The line graph L (G) of a graph is planar if and only if G is planar, Δ ≤ 4 and if deg v=4 for a vertex v of G, then v is a cut vertex.

Theorem 5 [1]. A graph is planar if and only if it has no subgraph homeomorphic to K₅ or K_3,3.

Theorem 6 [9]. For any planar graph G, edge semi entire block graph E_b (G) whose vertices have degree d_i has (q+r+b) vertices and

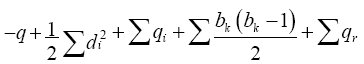
edges, where r the number of regions, b be the number of blocks, q_j the number of edges in a block b_j, b_k be the blockdegree of a cut vertex C_k and q_r be the number of edges lies on the region r₁.

Theorem 7 [3]. For any planar graph G, pathos edge semi entire block graph PEb (G) whose vertices have degree d_i has (2q+k+1) vertices and 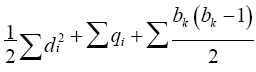edges, where r be the number of regions, b the number of blocks, q_j the number of edges lies in a block b_j, b_k be the block degree of a cut vertex C_k and q_r be the number of edges lies in the region r₁.

Theorem 8 [1]. A connected graph G is eulerian if and only if each vertex in G has even degree [5].

Theorem 9 [2]. A nontrivial graph is bipartite if and only if all its cycles are even.

Theorem 10 [3]. For any tree T, the pathos edge semi entire block graph PE_b (T) is planar if and only if T is a star graph K_{1, n}, for n ≥ 3.

Total Pathos Edge Semi Entire Block Graph

In this section, we define the total pathos edge semi entire block graph of a tree.

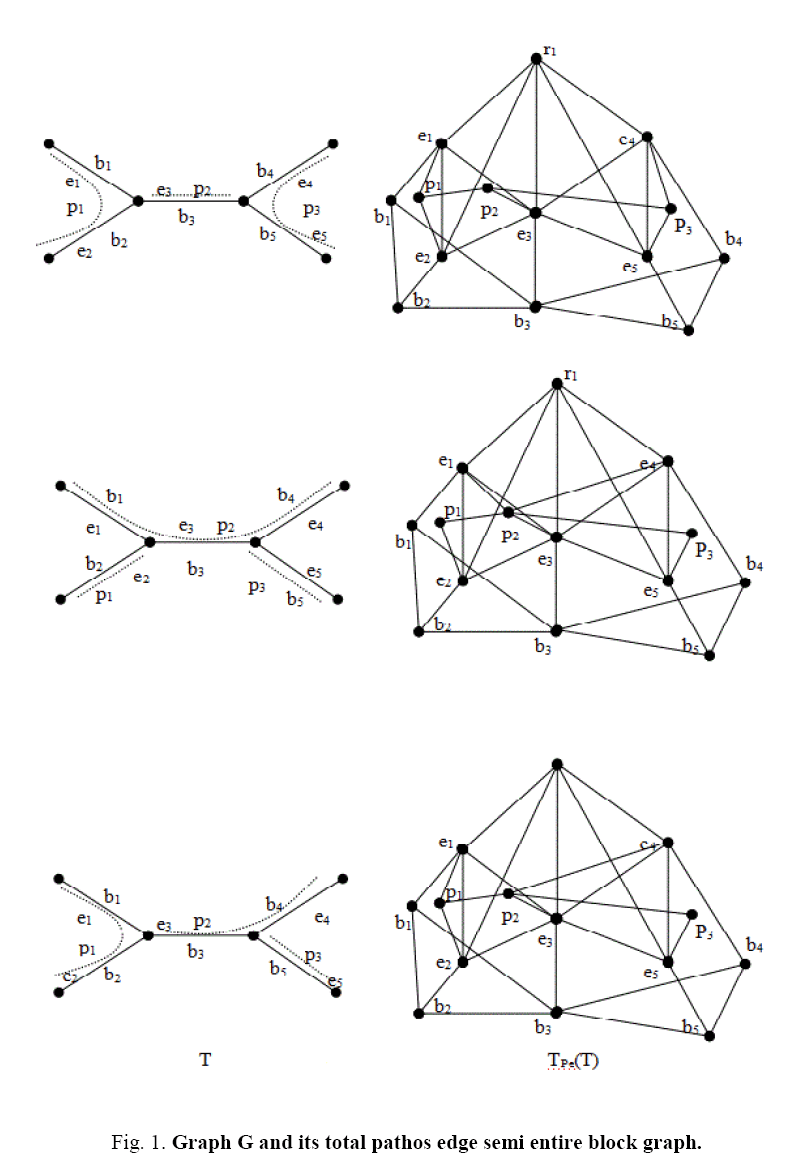
Definition 2.1 The total pathos edge semi entire block graph of a tree T denoted by T_Pe (T) is the graph whose vertex set is the collection of edges, blocks, regions and path of pathos of T in which two vertices of T_Pe (T) are adjacent if both are the edges of T which are adjacent or both are blocks of T which are adjacent or one is a block and other is an edge e of T and e lies on it, or one is a region and other is an edge e of T and edge e lies on the region or one is a path of pathos of T and other is an edge e of T in which e lies on the path or both are the path of paths p_i and p_j of T and both p_i and p_j have a common cut vertex. In Figure 1, a graph G and its total pathos edge semi entire block graph are shown [6].

We begin with the following direct results.

Remark 1. For any tree T,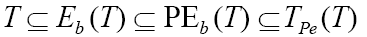

Remark 2. For any graph G, Tpe (G)=PE_b (T)U P (T)

Remark 3. For any edge e_i in T with edge degree n, the degree of the vertex e’_i which corresponds to e_i in T_Pe (T) is always n+1.

Results

Theorem 11. Let T be a tree, the total pathos edge semi entire block graph T_Pe (T) is always non-separable.

Proof. Consider T be a tree and let e_i for all i?T be the edges of T. In a Tree T, every edge becomes a block. Let b₁=e₁, b₂=e₂. b_m=e_m be the blocks, r₁ be the only one region in T and p₁, p₂. p_k be the pathos of T. By the definition of L (T), the vertices e₁, e₂. e_m of L (T) form a sub graph without cut vertex. Also in T_Pe (T), the vertex formed from the region called the region vertex is adjacent to e_i for all i=1,2. m, to form a nonseparable graph. Since there are m blocks which are K₂, we have each b_i is adjacent to e_i for all i.

Further T contains some pendent pathos, these correspond to the pathos vertices p_i and each p_i is adjacent to only one vertex e_j such that e_j becomes a cut vertex. Also in a tree, at least two paths are always adjacent then T_Pe (T) is non-separable [7].

Theorem 12. If T (p, q) is a connected graph whose vertices have degree d_i and if the number of blocks to which the edge e_i belongs in T is b_i, then the total pathos edge semi entire block graph T_Pe (T) has 2q+k+1 vertices and 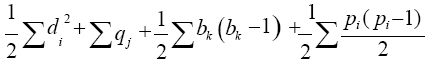edges, where q_j be the number of edges in each block b_jand bk be the block degree of a cut vertex c_k.

Proof. By Remark 1, 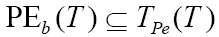Thus, the number of vertices in T_Pe (T) equals the number of vertices of of PE_b (T). By theorem 7, V[PE_b (T)]=2q+k+1.

Further by Remark 2, the number of edges in T_Pe (T) is same as the number of edges in PE_b (T) and the number of edges P(T).

By theorem 7, the number of edges in PE_b (T) is 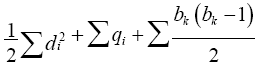. Also, the number of edges in a path graph P(T) is 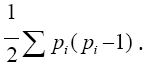Hence the number of edges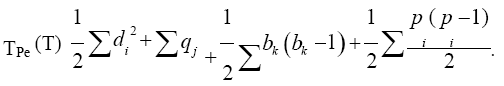

Theorem 13. For any tree T, T_Pe (T) is non-complete graph.

Proof. By definition of T_Pe (T), there is no adjacency between the regions and blocks. In T_Pe (T) there is no edge between the region vertex and block vertex. Hence T_Pe (T) is non-complete graph.

Theorem 14. For any tree T, the total pathos edge semi entire block graph T_Pe (T) is not a bipartite graph.

Proof. In a tree other than path contains at least one vertex v of T such that degree of v ≥ 3. Let e1, e2, e3 be the edges incident to v. By the definition of T_Pe (T), the edges incident with v, form a cycle C₃ in T_Pe (T). By Theorem 9, T_Pe (T) is not bipartite graph.

Theorem 15. For any tree T, T_Pe (T) ? PE_b (T) if and only if T is a path.

Proof. Let T be a path. By definition, T_Pe (T), PE_b (T) have the same number of vertices. Since T is a path and the pathos graph of a path has no edges, it implies by definitions that T_Pe (T) and PE_b (T) are isomorphic.

Conversely suppose T_Pe (T) ? PE_b (T) and T is non-trivial connected tree. We now prove that T is a path. We assume that T has at least one vertex v such that degree of v ≥ 3. By remark 2, the number of edges in T_Pe (T) is the sum of the number of edges PE_b (T) and the number of edges in P (T). Hence the number of edges in PE_b (T) is less than the number of edges in T_Pe (T). Thus T_Pe (T) ? PE_b (T), a contradiction. Thus, T is a path.

Theorem 16. For any tree T, total pathos edge semi entire block graph T_Pe (T) is always nonplanar.

Proof. Let T be a connected tree and be a star K_{1, n}, for n ≤ 3. By Theorem 10, PE_b (T) is planar. Let e₁=b₁, e₂=b₂, and e₃=b₃ be the edges which are also blocks, r₁ be the region and p₁, p₂ be the path of pathos of T. In T_Pe (T), the vertices e₁, e₂, e₃ and r₁ form a complete graph K₄. The block vertices b₁, b₂, b₃ form a complete graph K₃ and the edges between p₁ and p₂ must crosses the edges already drawn and hence T_Pe (T) is nonplanar.

If T=K_{1, n}, n ≥ 4, by the Theorem 10, PE_b (T) is nonplanar and hence T_Pe (T) is nonplanar.

Theorem 17. For any tree T, the total pathos edge semi entire block graph T_Pe (T) has crossing number one if and only if T is K_{1, 3}.

Proof. Suppose T_Pe (T) has crossing number one, clearly T_Pe (T) is nonplanar. By Theorem 16, we have T=K_{1, n}, n ≥ 4. Assume that T=K_{1, n} for n=4. By the definition of L (T), L (K_1,4)=K₄. Since every edge of T lies on only one region r₁ so in T_Pe (T), all vertices of K₄ are adjacent to the region vertex r₁ to form K5, clearly it has crossing number one. Further in a tree T, each edge is a block and all blocks b₁, b₂, b₃ and b₄ are adjacent to each other. By the definition of T_Pe (T), all four block vertices form K₄ as sub graph, clearly the inner vertex b_i is adjacent to the edge e_i which corresponds to e’i in T_Pe (T) which form another one crossing number. Hence T_Pe (T) has crossing number at least two, a contradiction [9,10].

Proving conversely, show that K₅ is a subgraph which has crossing number one. By the definition of line graph, L (K_1,3)=K₃ and all edges lies on only one region. In T_Pe (T), the region vertex r₁ is adjacent to all vertices 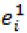which corresponds to the edges of T and it form a complete graph K₄ . Further each edge is a block and all blocks form K₃ as a sub graph. Also, the pathos vertices p1 adjacent is e₁ and e₂, p₂ is adjacent to e₃ and these pathos vertices are adjacent to each other and it form crossing number one. Hence, Cr [ T_Pe (T)]=1.

Theorem 18. For any tree T, the total pathos edge semientire block graph T_Pe (T) is Eulerian if and only if T is a star K_{1, 4n+2} for n ≥ 1.

Proof. Suppose T_Pe (T) is Eulerian. We consider the following cases.

Case 1. Assume that T be any non-star tree T, we have the following sub cases.

Sub case 1.1. Let u, v ?T such that degree (u)=3 and degree (v)=2. Let e₁, e₂, e₃ be the edges incident to u and e₃, e₄ be the edges incident to v. Clearly edge degree of an edge e₁ is 4. By the Remark 3, the corresponding vertex 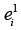in T_Pe (T) have degree 5, which is odd. By Theorem 8, T_Pe (T) is noneulerian, a contradiction.

Sub case 1.2. Assume that T contain an edge have edge degree of every edge is even, which is possible only when the total number of edges of T will be odd. By definition of TPe (T), the deg (ri) becomes odd. By Theorem 8, TPe (T) is noneulerian, a contradiction.

Case 2. Assume that T=K1, p where p ≠ 4n+2. We have the following subcases.

Sub case 2.1. We assume that T=K₁, 3n+1 n=1.2. k. By case 1, each edge of K₁, ₃ have edge degree 4, by Theorem 2, the corresponding vertices 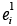in T_Pe (T) have edge degree odd, which is odd. By the Theorem 8, T_Pe (T) is noneulerian, a contradiction.

Sub case 2.2. Assume that T=K_1,4. By case 1, each edge e_i in T have edge degree odd. By the Remark 3, the corresponding vertices e1 in T_Pe (T) have even degree. The region vertex r’_i is adjacent to all four vertices v¹_i , i=1, 2, 3, 4 which form a graph with all vertices of even degree. In T, there are two paths of pathos p1 and p2 and each pathos contains two edges. In T_Pe (T), both pathos vertices adjacent to form graph with both p₁ and p₂ have odd degree. By Theorem 8, T_Pe (T) is noneulerian, a contradiction.

Conversely suppose T=K_{1, 4p+2} for p=1,2. n. In a tree T, every edge e_i have odd degree, by Remark 3, the vertices 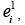corresponds to e_i of T in T_Pe (T) becomes even degree. Further the total number of edges of T is even, then the region vertex in T_Pe (T) becomes even degree. Also, each edge is a block e_i =b_i for all i, each block b_i adjacent to remaining blocks and e_i adjacent to b_i to form even degree. Lastly the pathos vertices which are adjacent to even number of edges and each pathos are adjacent to remaining 2n path of pathos. Then in T_Pe (T), every vertex is of even degree. Hence T_Pe (T) is Eulerian.

Theorem 19. For any tree T, T_Pe (T) is Hamiltonian.

Proof. Suppose T be a tree. We consider the following cases.

Case 1. Let T be a star K_{1, n}, n is odd with vertices u₁, u₂u₃.... u_nu_n+k such that degree of u₁=n and let b₁, b₂ . . .b_m be the number of blocks, ri be the regions, the number of paths of pathos are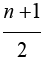 and T contains only one region. By the definition of T_Pe (T), V[T_Pe (T)]={e₁, e₂, e₃ . . . . . .e_n, b₁, b₂, . . . . . b_n-1} 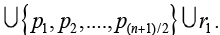Then there exist a cycle containing the vertices of T_Pe (T) as p₁,p₂, p₃,…p_k,e₅,e_k,b_kb_k-1,. . . b₁,e₁,e₃… r.e₂ p₁ and it includes all the vertices of T_Pe (T). Hence it is a Hamiltonian cycle.

Case 2. Let T=K_1,n, n>2 and is even. Then the number of path of pathos is 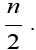Let V [T_Pe (T)]={e₁,e₂ . . . .e_n, b₁,b₂. . . b_n-1} U {p₁, p₂ . . . . . . 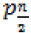} U r₁ then there exist a cycle which contains the vertices of T_Pe (T) as p₁, p₂,…e_k b_k, b_k-1, . . . b₁,e₁,…r.,e₂ p₁ and is a Hamilton cycle. Hence T_Pe (T) is Hamiltonian.

Case 3. Suppose T is neither a path nor a star, then T contains at least two vertices of degree >2. Let e₁, e₂. . . . .e_n be the edges of T such that e₁=b₁, e₂=b₂. . . . . e_n=b_n be the blocks. Then V [T_Pe (T)]={e₁, e₂ . . . e_n, b₁, b₂. . . .b_n}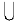 {p₁, p₂ . . . . .p_i}r₁ where T has p_i pathos vertices for i > 1 and each pathos vertex is adjacent to the edge of T, where the corresponding pathos lie on the edges of T. Then there exist a cycle C which contains all the vertices of T_Pe (T) as p1, e₁b₁e₂p₂e₃. . . . . . . . . r₁ en p₁. Hence T_Pe (T) is a Hamiltonian. Clearly T_Pe (T) is a Hamiltonian.

Case 4. Suppose T is a path. Let u₁, u₂u₃. . . . . u_n be a path. The vertex set V [T_Pe (T)]={e₁,e₂ . . . .e_n, b₁,b₂. . . b_n-1} U {p₁} U r₁ . Clearly there exist a cycle which contains the vertices of T_Pe (T) as p₁,…e_k b_k, b_k-1, . . . b₁,e₁,…r.,e₂ p₁ and is a Hamilton cycle. Hence T_Pe (T) is Hamiltonian.

Conclusion

In this paper, we defined the total pathos edge semi entire block graph of a tree. We characterized the graphs whose total pathos edge semi entire block graphs are planar, Hamiltonian and have crossing number one.

References

1. Harary F. Annals of New York. Academy of Sciences. 1977;175:198.
2. Harary F.Graph Theory. Addison-Wesley Reading Mass. 1969;72:107.
3. Jagadeesh N,Venkanagouda M Goudar.Pathos edge semientire block graph. J Com Math Sci.2015;6:395-402.
4. Kulli VR. On minimally nonouterplanar graphs, proceedings of the Indian National Science Academy. 1975;41.
5. Kulli VR,Akka DG. J Math Sci.1980;14:585-8.
6. Sedlacek J. Some properties of interchange graphs. The Graphs and the applications. Academic press, New York. 1962.
7. Stanton RG, Cowan DD, James LO. Proceedings of the Louisiana Conference on Combinatorics. Graph Theory and Computation. 1970;pp:112.
8. Goudar VM. On Pathos vertex, semientire graph of a tree.IntJApp Math Res. 2012;11:666-70.
9. Goudar VM,Jagadeesh N. Edge semientire block graph.Int J Com App.2014;89:42-4.
10. MaralabhaviYB, Muddebihal,Goudar VM. On Pathos edge semientire graph of a tree.In the Far East J App Math.2007;27:85-91.