Original Article
, Volume: 6( 1)The Origins of Gravitational Fields
- *Correspondence:
- Solomon BT , Chairman, Xodus One Foundation, 815 N Sherman St., Denver, CO 80203, USA, Tel: 3033766123; E-mail: bts@XodusOneFoundation.org
Received: December 06, 2016; Accepted: January 13, 2017; Published: January 25, 2017
Citation: Solomon BT, Beckwith AW. The Origins of Gravitational Fields. J Space Explor. 2017;6(1):111.
Abstract
This paper asks and addresses several questions. First, why don’t gravitational theories include near field gravity probes and gravity modification as part of the bigger picture? And therefore, the next question is, is the gravitational constant G a constant or a variable? Based on a study of 798 isotopes, this investigation shows that G is a variable and a function of the mass of the nuclei. Second, by showing that much of theoretical physics is cantered on the field structure, not the source, the paper asks the question, is mass the source of gravitational fields or is it a proxy for some other property of matter? By making some extrapolations of quark masses, the paper shows how quark motion, not quark mass, is the source of gravitational fields. Higgs field implicitly assumes that mass is a property that is external or extrinsic to the property of the particle. Finally, by asking the question is it possible to derive a description of mass that is intrinsic to the particle, and to its existing properties? Is it possible to derive a property of mass without adding anything new? By deriving a different mass model from Higgs Field, a particle structure that is consistent with both mass-based and massless particles is derived. This mass model suggests that the law of conservation of mass is not as fundamental as we thought it is. That particle radius plays an important part in this conservation law and could lead to the answer of the proton radius puzzle.
Keywords
Higgs; Gravitational constant; Quark mass; Conservation of mass; Gravity modification; Gravity probes; Proton radius puzzle
Introduction
In 2015, Steinhardt and Esftathiou [1] stated that the Planck Space Telescope data shows that the Universe is simpler than had been thought and that both string and quantum theories require revisions. To add to this debate, in 2012 using Fermi Gamma-Ray Space Telescope photographs of gamma ray burst, Nemiroff [2] showed that quantum foam could not exist. One could probably qualify this finding by restating that quantum foam could not exist in the absence of matter but such a proof would be very difficult to arrive at. A year later, Solomon [3] proposed that both exotic matter and strings could not exist and in 2010 [4] and 2015 [5] Solomon had proposed that photon probability could not be Gaussian.
Exotic matter cannot exist because it leads to perpetual motion machines. Bondi [6] proposed that negative mass was consistent with General Relativity and negative mass or exotic matter would gravitationally repel while positive mass or normal matter would gravitationally attract and if the “motion is confined to the line of centers, then one would expect the pair to move off with uniform acceleration.”
There are two issues with this first problem. The first is perpetual motion physics. Attach two thin capsules to two radial spokes. The other end of these spokes are attached to the axis of an electric generator. The spokes are fixed a small angle apart so that the capsules are close to each other. The capsules are very, very thin so as to remove any significant complications with the normal matter of the thin capsule material. In one capsule insert exotic matter, and in the other insert normal matter. Release the spokes. What does one observe? Per Bondi’s “one would expect the pair to move off with uniform acceleration” one observers that the attraction-repulsion caused by the normal-exotic matter interaction would turn the electric generator to produce electrical energy. One concludes that exotic matter results in perpetual motion, a sacrilege in physics. Therefore, since Nature abhors perpetual motion, one infers that exotic matter cannot exist in nature.
The second issue, however, is subtler. The esteemed Bondi [5] was able to authenticate exotic matter using General Relativity or rephrasing, General Relativity was able to endorse perpetual motion physics. Therefore, any physical theory that uses exotic matter is now doubtful. The lesson here is that one has to be careful not to modify or develop a theory that leads to perpetual motion physics. Since Klein [7] has stated that mathematics has become so powerful that it can now be used to prove anything, there needs to be an alternative approach to developing mathematical models for physics. Therefore, the urgent need for the extensive use of empirical data and process models to guide this mathematical development not the other way around. This raises the concern that quantum theory could suffer from similar types of endorsement.
Solomon [3] proposed that strings could not exist because they contradict Lorentz-FitzGerald Transformations (LFT). Macro body elongation due to tidal gravity is attributed to Roger Penrosei. Macro bodies elongate as the body falls into a gravitational field. Let’s re-examine this tidal behaviour with the additional requirement that this tidal gravity property be consistent with LFT or special theory of relativity (STR). To be consistent with LFT, the atoms and elementary particles would contract in the direction of the fall. However, to be consistent with tidal gravity’s elongation, the distances between atoms in the macro body has to increase at a rate consistent with the acceleration and velocities experienced by the various parts of the macro body. That is, as the atoms get flatter, the distances apart get longer. This should be named the Tidal Axiom. One suspects that string theory’s axiom, that strings expand with energy, is inconsistent with the Tidal Axiom and has led to an explosion of string theories, each trying to explain Nature with no joy.
Solomon [3,8-10] proposed that contemporary physics can be categorized into three types of particles, inelastic and point-like (quantum theory), tensile (strings) and compressive. Assuming that particles were compressive Solomon [3,8-10] proved that a new equation for gravitational acceleration (1) that does not require a prior knowledge of the amount gravitating mass, thereby strengthening the case that strings cannot exist.
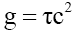 (1)
(1)
Where τ is the spatial gradient of the time dilation transformation or change in time dilation transformation divided by that distance, and noting that the time dilation transformation is the ratio of tv/t0 per LFT or (2), and Newtonian gravitational transformations (NGT) or (3). Table 1 shows for comparisons between actual and proposed (1) gravitational accelerations. Thus Solomon’s [3,8-10] g=τc2 provides a mathematical solution to Hooft’s [11] assertion that “absence of matter no longer guarantees local flatness”. Solomon then showed [8-10] that (1) is valid for mechanical and electromagnetic forces.
| Gravitational | Acceleration | Error in g | Change in Time Dilation | Gravitationally Distorted | |
|---|---|---|---|---|---|
| Heavenly | g=GM/R2 | g=τc2 | Transformation Across Particle | Distance | |
| Body | (m/s2) | (m/s2) | PPM (Parts Per Million) | (m) | |
| Earth | 9.8028931 | 9.8028931 | -0.0020876 | 1.09E-27 | 9.99E-12 |
| Jupiter | 24.868616 | 24.868618 | -0.0592693 | 2.77E-27 | 9.99E-12 |
| Mars | 3.8205065 | 3.8205065 | -0.0004323 | 4.25E-28 | 9.99E-12 |
| Mercury | 4.0235485 | 4.0235485 | -0.0003277 | 4.47E-28 | 9.99E-12 |
| Neptune | 11.26517 | 11.26517 | -0.0092878 | 1.25E-27 | 9.99E-12 |
| Pluto | 0.6054524 | 0.6054524 | -2.324E-05 | 6.73E-29 | 9.99E-12 |
| Saturn | 10.563045 | 10.563045 | -0.0211201 | 1.17E-27 | 9.99E-12 |
| Sun | 280.30204 | 280.30385 | -6.4559109 | 3.12E-26 | 9.99E-12 |
| Uranus | 8.7588541 | 8.7588541 | -0.0075138 | 9.74E-28 | 9.99E-12 |
| Venus | 8.8738716 | 8.8738716 | -0.001798 | 9.87E-28 | 9.99E-12 |
Table 1: Gravitational acceleration values using Newtonian equation and equation (1), for a particle diameter of 10-11 m.
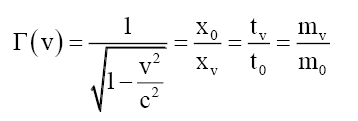 (2)
(2)
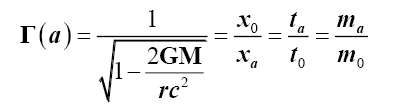 (3)
(3)
Or in the generic form, the environmental transformation Γ(e),
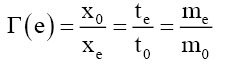 (4)
(4)
Notes
• Though the data presented is only to 15 decimal places, all numerical analyses were conducted to 250 significant digits using G of 6.67259 × 10-11.
• The numerical results validate equation (1), that gravitational acceleration can be derived without reference to its mass source as the errors between Newtonian g (Column 2) and Ni Field g (column 3) is < |6.5| ppm.
• Combining all recent experimental results [12] provides measured range of between 6.671 × 10-11 to 6.676 × 10-11 or a mean of 6.6738 × 10-11 and standard deviation of 0.0012 × 10-11 that the true G is in this range.
• These near field gravity probe G measurements are a good example of precision versus accuracy and proof of the presence of systematic errors.
Another example where further research is warranted is the Alcubierre warp drive [13] as a means to interstellar propulsion which is based on general relativity using exotic matter to warp spacetime. Note the problems with exotic matter as stated above. As pointed out earlier with Bondi’s exotic matter, general relativity (GR) may not provide meaningful results in these extreme conditions. However, there is a more serious axiomatic problem. Beckwith [13] states that “in assuming violation of conservation of energy, within the confines of a local universe, as modelled either by steady state models, or the usual FRW universe structure, one is by necessity appealing to a multiverse structure, i.e. multiple universes. However, unless one explicitly models the evolutionary history of the universe, used by the Alcubierre warp drive, as a multiverse, one is using a single universe, but implicitly assuming a physical process which could only work if a multiverse structure exists. Hence, the Alcubierre warp drive program, modelled within a single universe, is appealing to a multiverse structure in order to allow for its local universe violation of conservation of energy to occur. By any physical reasoning, the result is a reducto absurdum which is not supported by logic”.
This suggests that though the Alcubierre warp drive theory is mathematically solid and provides a mechanism for warp drive, there are axiomatic errors in this theory. A rethink without the use of exotic matter would be interesting as it could be the proof of the existence of a multiverse.
Therefore, pursuing Steinhardt and Esftathiou’s [1] need for a different approach to the physics of the Universe, one can broaden the scope of gravitational theories by requiring that new theories are consistent (1) distant cosmology, (2) near field local gravity probes, and (3) local gravity modification.
In 2015 using this broadened framework Solomon [14] proposed two new theoretical considerations. First, that gravitational fields are indeed produced by quark motion not mass, and that mass is only a proxy for amount of matter. Second, a 4th approach to forces that is not related to relativity, string or quantum (RSQ) theories, that a particle’s velocity and acceleration is evidenced by the shift in the Center of FieldCF of the local field’s spatial gradient. This field could be gravitational, electromagnetic, electric, magnetic or mechanical motion.
Solomon [14] proposed that the deformation of this field results in the shift in the Center of FieldCF, just as altering the shape of an object would alter its Center of MassCM. The magnitude and direction of the shift in this CF governs the strength and direction (attraction or repulsion) of the resulting motion of this Field. For example, in a gravitational field, NGT would induce non-linear length contraction, mass increase and time dilations across an elementary particle. The net effect on a particle’s spherical shape (external to a gravitational field) was the deformation (in a gravitational field) to an asymmetrical ovoid-like shape thereby causing the particle’s centre of mass to shift towards the gravitating mass evidenced as acceleration. Using the Centre of Mass concept, the Centre of FieldCF of a field F that ranges from lower limit L to upper limit U, is defined as
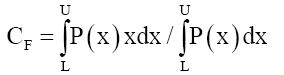 (5)
(5)
Where P is the property of the Field used to evaluate the Field’s CF. The relevant field property depends upon the type of deformation applied to this field. If the deformation of the field property is non-linear then the spatial gradient of the Field’s property P or dP/dx is the parameter used to estimate the Field’s CF. If there is no deformation of the field property, then the field’s property P is the parameter used to estimate the Field’s CF as the spatial gradient of P is zero. The importance of this finding is that Poincaré stresses [15] no longer exists as electric field lines and therefore magnetic field lines are no longer repulsive. See Table 2, errors between classical electric fields and the Centre of FieldCF approach for electric fields.
| QR | 0.3333 | 0.66667 | 1 | 1.33333 | 1.66667 | 2 | 2.33333 | 2.6667 | 3 | 3.33333 | 3.66667 | 4 | 4.33333 | 4.66667 |
| QL | ||||||||||||||
| 0.333 | -0.58% | -0.26% | -0.15% | -0.09% | -0.07% | -0.07% | -0.09% | -0.11% | -0.16% | -0.21% | -0.28% | -0.36% | -0.45% | -0.56% |
| 0.667 | -0.23% | -0.11% | -0.06% | -0.03% | -0.01% | 0.01% | 0.01% | 0.02% | 0.02% | 0.02% | 0.01% | 0.00% | -0.01% | -0.03% |
| 1 | -0.11% | -0.06% | -0.03% | -0.02% | 0.00% | 0.01% | 0.02% | 0.02% | 0.03% | 0.03% | 0.03% | 0.03% | 0.03% | 0.03% |
| 1.333 | -0.05% | -0.03% | -0.02% | -0.01% | 0.00% | 0.01% | 0.01% | 0.02% | 0.02% | 0.03% | 0.03% | 0.03% | 0.04% | 0.04% |
| 1.667 | -0.01% | -0.02% | -0.01% | -0.01% | 0.00% | 0.00% | 0.01% | 0.01% | 0.02% | 0.02% | 0.02% | 0.03% | 0.03% | 0.03% |
| 2 | 0.01% | -0.01% | -0.01% | -0.01% | -0.01% | 0.00% | 0.00% | 0.01% | 0.01% | 0.02% | 0.02% | 0.02% | 0.02% | 0.03% |
| 2.333 | 0.03% | 0.00% | -0.01% | -0.01% | -0.01% | 0.00% | 0.00% | 0.00% | 0.01% | 0.01% | 0.01% | 0.02% | 0.02% | 0.02% |
| 2.667 | 0.04% | 0.00% | -0.01% | -0.01% | -0.01% | -0.01% | 0.00% | 0.00% | 0.00% | 0.01% | 0.01% | 0.01% | 0.01% | 0.02% |
| 3 | 0.05% | 0.01% | 0.00% | -0.01% | -0.01% | -0.01% | -0.01% | 0.00% | 0.00% | 0.00% | 0.01% | 0.01% | 0.01% | 0.01% |
| 3.333 | 0.06% | 0.01% | 0.00% | -0.01% | -0.01% | -0.01% | -0.01% | -0.01% | 0.00% | 0.00% | 0.00% | 0.00% | 0.01% | 0.01% |
| 3.667 | 0.06% | 0.01% | 0.00% | -0.01% | -0.01% | -0.01% | -0.01% | -0.01% | -0.01% | 0.00% | 0.00% | 0.00% | 0.00% | 0.01% |
| 4 | 0.07% | 0.02% | 0.00% | -0.01% | -0.01% | -0.01% | -0.01% | -0.01% | -0.01% | -0.01% | 0.00% | 0.00% | 0.00% | 0.00% |
| 4.333 | 0.07% | 0.02% | 0.00% | -0.01% | -0.01% | -0.01% | -0.01% | -0.01% | -0.01% | -0.01% | -0.01% | 0.00% | 0.00% | 0.00% |
| 4.667 | 0.08% | 0.02% | 0.00% | -0.01% | -0.01% | -0.01% | -0.01% | -0.01% | -0.01% | -0.01% | -0.01% | -0.01% | 0.00% | 0.00% |
Table 2: Error (%) between classical and centre of field method between left QL and right QR charged Particles.
The Unanswered Question in Gravitational Physics
Pursuing Steinhardt and Esftathiou’s [11] there is a need for a different approach to gravity. One can expand the scope of this need by requiring that new theories on gravity are consistent in their modeling of how Nature works from the perspective of (1) distant cosmology, (2) near field local gravity probes, and (3) local gravity modification. Broadening the field to include near field local gravity probes and gravity modification introduces more avenues for exploration. Various researchers [13-15] using near field gravity probes have shown that it is very difficult to concur on a specific value for the gravitational constant G. This strongly suggests that gravity does not behave exactly as one would like it to and therefore, there is more to gravity than we currently understand or recognize.
Gravity modification introduces another dimension to the gravity problem. What if gravity was not caused by mass? Podkletnov [16,17] had reported gravity shielding effects above a spinning superconducting ceramic disc. Podkletnov’s results have not been reproduced because other experimenters [18,19] ceramic discs cracked before reaching Podkletnov’s disc spin requirements. This is unfortunate as (1) suggest that these experiments ought to be successful. Solomon [8] has suggested an approach to deconstructing Podkletnov’s experiments with the expectation that future experimenters can avoid the mistakes of past experiments [18,19]. The importance of these gravity modification experiments is that they can lead to the confirmation that mass is not necessary for gravitational fields and therefore, matter and not mass is the cause of gravitational fields.
Thus, an approach to new avenues of research lies in theories similar to General Relativity in that they are not particle based. In Newtonian gravity, rest mass generates gravitational effects directly by the translation of potential energy to kinetic energy. In General Relativity [20], all sources of both energy and momentum contribute to generating spacetime curvature and that the energy-momentum tensor Tαβ is the source of the space time curvature. This curvature then causes the effect of a body falling in a gravitational field.
In this paper, unlike Newtonian gravity or General Relativity, the importance of the shape of spacetime lies in the fact that it informs us of what time dilation and length contraction are, as these two parameters are the minimum information required to determine gravitational acceleration. Therefore, the formalism in this paper will be different to that of Newtonian gravity or General Relativity, as a tensor treatment is outside the scope of this paper.
A schema is an outline of a model of a complex reality to assist in explaining this reality. The work of various researchers [6] in the gravity field can be presented by a conceptual formalism referred to as source-field-effect schema. The source-fieldeffect schema corresponds to the mass-gravity-acceleration phenomenon, respectively.
Puthoff’s [21] source-field schema describes how the mass source could create a gravitational field; how GR’s curved spacetime could be produced by the polarizability of vacuum in the vicinity of a mass. Rueda and Haisch [21] source schema is about mass only. They discuss inertia mass, mass as a field and Higgs boson as the origin of mass. Bondi [22] suggested the possibility of a field schema not requiring mass. Bondi [22] made two observations when reviewing gravitation as a theory and suggested that mass may not be critical to a theory of gravitation. First, as “long as relativity is considered purely as a theory of gravitation, the inertial and passive gravitational masses do not in fact appear”. This is consistent with the fact that gravitational acceleration (but not force) is independent of the mass of the object being accelerated. His second observation was that “active gravitational mass occurs for the first time as a constant of integration in Schwarzschild’s solution” suggesting the possibility that this constant of integration could have other experimentally untested interpretations. One could conjecture that mass is a proxy for number of quarks and therefore a proxy for quark interaction as the source of gravitational fields. Bondi did not explicitly say it, but maybe one should look into other mechanisms for gravitational field sources.
Hooft [11] takes another step in Bondi’s direction with his source-field schema. He states that the “absence of matter no longer guarantees local flatness” that the absence of mass does not guarantee that acceleration will not be present. In effec t the field is being disengaged from its source. Wagoner describes a local-field schema, how a gravitational field “emerges from a local analysis” leading to a broad class of metric theories. Solomon’s [6] schema proposed a different local analysis, one where local field distortions lead to a local field acceleration function, g=τc2, thereby providing a mathematical solution to Hooft’s [11] assertion that “absence of matter no longer guarantees local flatness”.
Having [2] proposed contemporary physics can be categorized by three types of particles, inelastic and point-like (quantum theory), tensile (strings) and compressive, contemporary physics recognizes three types of schema, (i) General Relativity or a geometric surface schema, (ii) Quantum Mechanics or inelastic point like elementary particle based schema, and (iii) String Theories or tensile strings based schema. This paper proposes a fourth type of schema that is closer to GR but with compressive elementary particles.
Using General Relativity’s [21] separation vectors this schema approach is presented by equations (6) to (9). Equation (6) presents the standard z-direction separation vector as a function of gravitational mass m, and gravitational constant G at a distance r from the source. Gravitational acceleration g can be defined in terms of separation vectors by equation (9). This three-part schema can be described as, i) the mass source or equation (7), ii) the field or equation (8), and iii) the field effect or acceleration, equation (9).
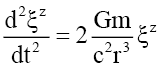 (6)
(6)
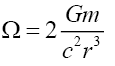 (7)
(7)
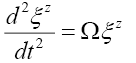 (8)
(8)
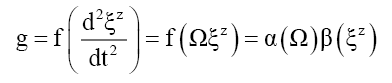 (9)
(9)
Where α and β are functions.
It is only necessary to limit this paper to the third part, equation (9), and unlike Newtonian gravity or GR [21], the importance of the shape of spacetime lies in the fact that it informs what time dilation, mass increase and length contraction are and thus their respective spatial gradients.
If General Relativity [21], models gravity as the change in the shape of spacetime, the curving of spacetime to cause this effect of gravity, one could propose an equivalent shape change on a non-point sized particle; that the change in the shape of spacetime in the local region of the particle is mirrored by an identical change in the shape of the particle. This is not macro body deformation due to the gravitational gradientii but particle-level deformation due to space contraction, time dilation and mass increase. The resulting deformation of the particle’s shape is evidenced as a shift in the center of fields of its massvolume ‘field’.
This is a logical extension of the inertia Lorentz-Fitzgerald transformations (LFT) Γ(v), equation (2), and the Newtonian noninertia gravitational field transformation (NGT) Γ(a), equation (3).
Solomon [6,9] proposed that this mass-volume field deformation was due to the internal effects of the NGTs Γ(a), present in the local region of the external gravitational field such that the spacetime transformations Γs(x,y,z,t) are concurrently reflected as particle transformations Γp(x,y,z,t) or,
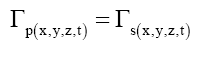 (10)
(10)
The utility of equation (10) is that it explains why the gravitational field passes through all matter. The proposed formalism of (6) to (9) therefore begs two questions,
• Can near field gravity probe experiments be improved to determine more accurately the gravitational constant G by developing a more sophisticated version of (7)?
• Can gravity modification be realized per (9) by deriving an alternative to the α(Ω)function to replace the mass source?
Of course, one could propose from a quantum theoretic perspective that gravitons are the source of gravitational fields, but these have not been proven to exists; and, at least just yet, does not allow for a scope enlarged gravitational theory that neither accounts for near field gravity probe experiments nor includes gravity modification as a theoretical study.
Rethinking the Matter-Gravity Relationship
A matter-gravity hypothesis has to address several issues:
What is the matter-gravity relationship?: Equation (9) shows that even though our theories on gravity are very sophisticated they do not address how matter creates the gravitational field.
Unknown systematic error: “Despite the increasing precision of some 300 modern-day near field experiments different labs have found slightly different values for the gravitational constant G, and in recent years the discrepancy has widened rather than narrowed [15,16]. In the opinion of the authors an unknown systematic error is present, therefore, a matter-gravity hypothesis would need to propose how these experiments could be improved.
Gravitational constant G is a variable: A second cause of measurement discrepancy could be that the gravitational constant G is not a constant. G could be a variable dependent upon some independent matter related factor, thus causing systematic error. Therefore, a matter-gravity hypothesis would need to address whether the gravitational constant is a constant or not.
Mass is a proxy for matter: Solomon [2] had proposed that mass was a proxy for matter. The G measurement discrepancies would affirm such a proposal as the near field gravity probe experiments show that same amount of mass does not deliver repeaTable measurements. Therefore, if such a proxy relationship does exist, any matter-gravity hypothesis will need to address, how mass could be a proxy for matter.
Mass of heavenly bodies: Because the Earth is our laboratory, the mass of any heavenly body is determined by the product of the Earth’s mass, ME, and the Earth-based gravitational constant, GE, or GEME, and therefore, even though GEME and GHMH for heavenly body H, is well understood, variations in GE will cause variations in known masses MH of these heavenly bodies. Should the gravitational constant G, change by some unknown factor, would it alter the estimated masses of heavenly bodies?
There are two parts to this investigation,
• Is the gravitational constant G a constant or dependent on some other independent factor?
• How and why is mass a very good proxy for the source of gravitational fields?
Addressing the first part (i) provides some means of either eliminating or introducing factors that may alter G. Knowing that gravity is mass dependent suggests an investigation into nuclei properties as independent factors. It is shown (see Appendix A and B), that the gravitational constant G is a composite (11) of the isotopic gravitational constants Gi(12) of element i and is dependent upon the isotopic mass Mi of the element.
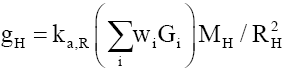 (11)
(11)
Where gH is the gravitational acceleration of a heavenly body, and the aggregation constant at radius R, ka,R = 2.244171 × 1025 for Earth-based observations, such that,
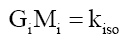 (12)
(12)
And isotope constant, kiso=2.973856 × 10-36 m3s-2. Thereby, proving that the gravitational constant G, is not a constant but a variable Gi that is dependent on the isotopic mass Mi of element i.
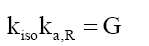 (13)
(13)
that is, G is the well-known gravitational constant G=6.67384 ×10-11 m3kg-1s-2.
Therefore, one concludes that G is determined by nuclei related factors, with mass directly or indirectly altering the value of the isotopic gravitational constant Gi. Part (i) explained.
Addressing the second part requires factors that are sTable to both nucleons, specifically, protons and neutrons. Quarks are one alternative, but this requires a determination of their masses that would most likely agree with the empirical evidence. Yet this is not forth coming. The Quark Velocity Model (Appendix C) suggests that quarks ‘orbiting’ the nucleons at vq =299,775,269 m/s, close to the velocity of light c, with up MU and down MD quark masses of 3.343167638 and 3.356973524 MeV, respectively.
In effect at the boundary of the RMS charge radius ri,c, there is an impulse type step-down from the tangential quark velocity vq, to the radial step-down equivalent to the gravitational escape velocity vs,r. This implies that the nuclei matter medium is substantially different from that of spacetime and has special properties. The empirical impulse type step-down velocity relationship is,
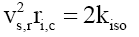 (14)
(14)
To be presented in a future paper.
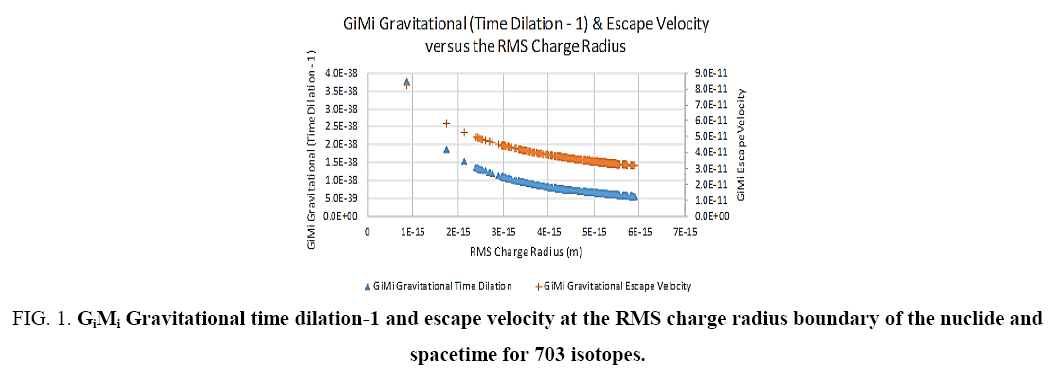
Equation (14) therefore, determines the time dilation present at the outer boundary (RMS charge radius ri,c) of the nuclei. See Figure 1. At this boundary these NGT transformations present at the starting of the gravitational field spread out from ri=ri,c into spacetime, to ri =∞, as a function of the radial distance ri.
Figure 1: GiMi Gravitational time dilation-1 and escape velocity at the RMS charge radius boundary of the nuclide and spacetime for 703 isotopes.
In gravitational fields, the relationship between orbital (tangential) Vorbit and escape (radial) velocity vescape is
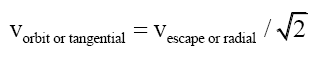 (15)
(15)
Therefore the equivalent step-down tangential velocity vs,t is,
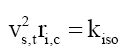 (16)
(16)
Just as light refracts in slower materials, the impulse type step-down function for isotope i could be due to nuclear refraction ηi, that the quark velocity vq refracts to the step-down tangential velocity vs,t,
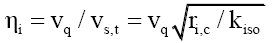 (17)
(17)
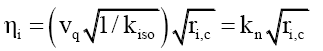 (18)
(18)
Where nuclear refractive constant kn=1.73834 × 1026.
Figure 1 strongly suggest that (12) is correct and new experiments in near field gravity probes should confirm (12). (16) therefore, determines the time dilation, per NGT(3), present at the outer boundary (RMS charge radius Ri,C) of the nuclei at a radial distance ri, from the start of the gravitational field ri=Ri,C, into spacetime, to ri =∞.
Therefore, this paper has shown, that though mass is a very good proxy for gravitational field source, it is the quark motion that generates gravitational fields. Thus, as mass is a measure of the amount of quarks in matter, mass is therefore, a good proxy for the origination of gravitational fields. Part (ii) explained.
Exploring the Possible Mass Relationships
Are particle structures dependent upon the existence of their external environment or are they internally derived and independent of the external environment? The constancy of the electron charge would suggest the latter. While the Higgs Field provides an explanation for particle mass, this theoretical approach is the former and dependent upon an environment that is external to the particle. This paper proposes the latter, an alternative mass mechanism that is derived from the internal properties of the particle.
The photon probability [18,19] is a disc, formed by the radius rP along the x- and y-axis, that is orthogonal to its motion vector (z-axis), like a flat umbrella. This umbrella like structure explains why electrons in the electron shell do not exhibit synchrotron radiation; their motion vectors are pointing at the nucleus.
In the search for an internal particle structure basis for mass, a review of the known empirical (or derivable from empirical) properties of mass shows,
• Mass is a scalar quantity, and additive.
• Mass is time invariant and therefore, either an entity on its own or a spatial function.
• The Velocity Quark Model (Appendix C) indicates that nuclear quark mass MQ consists of two parts basic mass MQB, and relativistic mass, MQR.
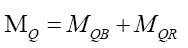 (19)
(19)
This paper is focused on quark basic mass, MQB.
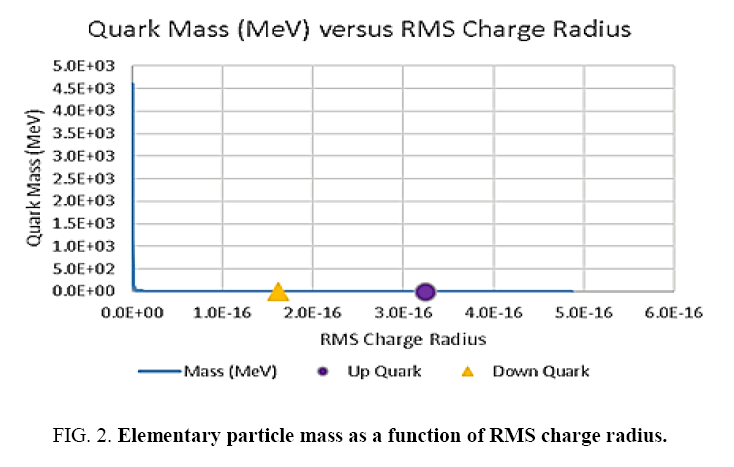
Since the up and down quark masses only slightly different, but their charge and RMS charge radii are exactly twice, suggest that mass has a non-linear relationship with respect to Ri,C the RMS charge radius ( Figure 2). Rewriting quark masses,
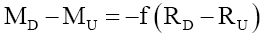 (20)
(20)
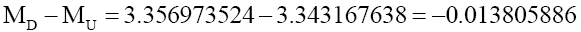 (21)
(21)
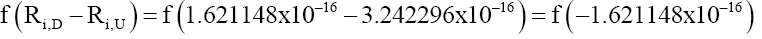 (22)
(22)
(20) suggests that mass is a very long tailed spatial function. This would fit the probabilistic density envelope function φM which is a long-tailed function. Proposing that like photon probability, whose radial distance rP is upper bounder rPU per D(12), the mass function is capped by the particle radius RM; and observed as mass, is only observable as mass if it is within the particle radius RM. The de Broglie equation (23) for a particle of mass MF with a velocity VF, its wavelength λM suggest that the mass-particle of wavelength λM has a Probabilistic Wave Function ψM (25) that is identical (24) to that of the photon of the same wavelength λP. This is because similar effects have to have similar causes if Nature is to be considered consistent everywhere.
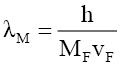 (23)
(23)
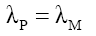 (24)
(24)
Therefore,
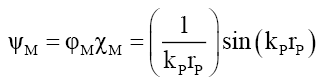 (25)
(25)
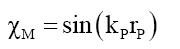 (26)
(26)
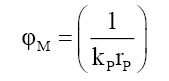 (27)
(27)
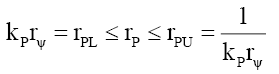 (28)
(28)
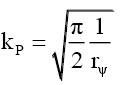 (29)
(29)
Deriving the mass model
To find a mass model that works, numerical integration trial and error models were developed until a very good solution was found. The probabilistic density envelope function φM was the basis for determining the relationship between the up and down quark estimated masses MU, MD, and their RMS charge radii, RU, RD, respectively. This was a multistep iterative process.
First step: This numerical mass model is divided into concentric rings of radius ri and thickness δr=3.242296 × 10-19. The mass probability intensity Ii, along a radial distance governed by the probabilistic density envelope function φP, is uniformly spread across each disc i such that,
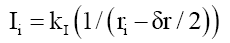 (30)
(30)
Where ri-δr/2 is the middle distance between any to concentric rings ri-1 and ri, and kI is the intensity coefficient that converts probability into mass. The mass of concentric ring Mi is the total mass probability intensity πIi 2 (per area of a disc) within a concentric ring, is that proportion of the concentric ring formed by the ratio of the larger disc ri to the smaller disc ri-1 or,
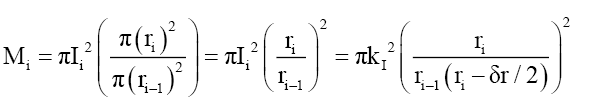 (31)
(31)
Therefore, the total cumulative mass along the radius of the disc formed by the probabilistic density envelope function φP is
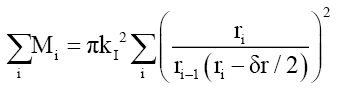 (32)
(32)
Solving analytically using quark masses, gives the value of πkI 2=1.302866 × 10-19MeVm2, with the MU, MD, mass errors of 0.204% and -0.223%. (32) shows the form of the mass relationship.
Second Step: Since, the first step suggests an inverse square relationship to the RMS charge radii, RU and RD, a regression model (R2=0.972510) from this numerical data was tested. It gives a quark mass model of the form (33). Figure 2.
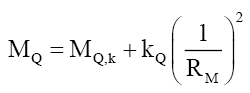 (33)
(33)
Third step: Solving analytically to get precise coefficient values, gives the mass coefficient kQ=4.837804891 × 10-34MeVm2 and the mass constant MQ,k=3.338565676 MeV. Strongly suggesting that mass is derived (26) and (27) from particle probability. One can propose that it is VEP matter that converts probabilistic density envelope function φM into mass as both are constrained by the nuclei/nucleon particle radius RM. As a caution, many alternative models were evaluated to test for the stability of kM (33). These produced inconsistent results and were abandoned.
VEP=Variable Electric Permittivity matter, to be published in a future paper.
Inferences About Quarks
See Table 3. In the limit as RM→∞the minimum quark mass MQ,∞=MQ,k=3.338565676 MeV, and the maximum quark mass MQ,0→∞MeV occurs as RM→0. One infers,
| (1) | (2) | (3) | (4) | (5) | (6) | (7) |
|---|---|---|---|---|---|---|
| Particle | Charge (e) | Rest Mass (MeV) | Rest Mass (kg) | Radiusii | KQ/Rp2 (MeV)iii | Comments |
| Up Quark | 0.6666667 | 3.34E+00 | 5.96E-30 | 3.24E-16 | 4.60E-03 | incorrect |
| Down Quark | -0.3333333 | 3.36E+00 | 5.98E-30 | 1.62E-16 | 1.84E-02 | incorrect |
| Pk,U | 0.6666667 | 3.34E+00 | 5.95E-30 | 1.20E-17 | 3.34E+00 | correct |
| Pk,D | -0.3333333 | 3.34E+00 | 5.95E-30 | 1.20E-17 | 3.34E+00 | correct |
| PΔ,U | 02-Mar | 4.60E-03 | 8.20E-33 | 3.24E-16 | 4.60E-03 | correct |
| PΔ,D | 01-Mar | 1.84E-02 | 3.28E-32 | 1.62E-16 | 1.84E-02 | correct |
| Electron | 1 | 5.11E-01 | 9.11E-31 | 3.08E-17 | 5.11E-01 | correct |
| Neutrino | 0 | 3.80E-07 | 6.77E-37 | 3.57E-14 | 3.80E-07 | correct |
Table 3: Mass model for a velocity of 58.455215 × 10+6 m/s or 19.498561% c.
• Quark basic mass MQ,B ≥3.338565676 MeV which agrees with known quark masses.
• The electron’s mass Me coefficient kM or constant MQ,k is different as Me<MQ,∞.
• Electrons belong to a different mass-familyF0 of particles than quark-family FQ.
Using (20) to deconstruct quark masses into an alternative particle form,
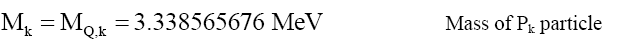 (34)
(34)
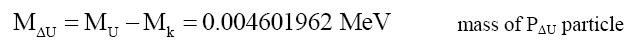 (35)
(35)
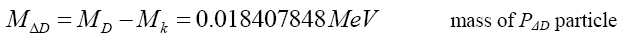 (36)
(36)
One can propose that Mk behaves like a fundamental particle Pk, as Mk>>MΔU and Mk>>MΔD, and that it is the Pk particle that is the carrier of the quark charge. The remainder is a delta particle PΔ. Then from (33) with MQ,k=0 the radius Rk of particle Pk is (Table 3).
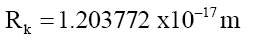 (37)
(37)
which is smaller than either quarks or the electron. The electron radius Re=3.061992 × 10-17 m (Table 3) is within the expectation that the electron (volume) is much smaller (23,322x) than the proton, and therefore, a good estimate to test experimentally with. More research is required to determine if Pk particles (34) exists.
• The results are independent of the selected velocity
• Radii of Up and Down quarks from [14] and not from (38).
• Calculate from (41) and (42) for the Up and Down quarks, respectively. Note these calculated masses do not match quark masses.
Properties of the mass model
The general mass relationship (33) can be rewritten as,
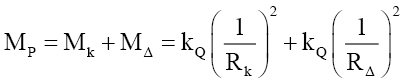 (38)
(38)
With,
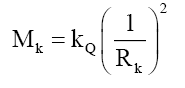 (39)
(39)
And therefore, to double check these results, from (38), for the up or down quark, respectively,
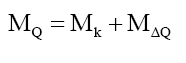 (40)
(40)
And verifying numerically (Table 3),
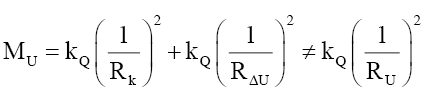 (41)
(41)
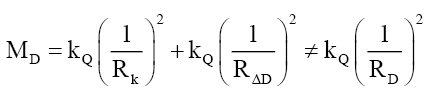 (42)
(42)
The important results from (38) and (39) are,
• When Mk=0, particles e, ν, Pk, PΔU, and PΔD are fundamental particles PF of mass MF and radius RF,
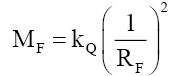 (43)
(43)
• Given a fundamental particle PF mass, one can derive their particle radius, RF per (43).
• As mass is additive, by (38) the sum of the masses of i fundamental particles Pi,
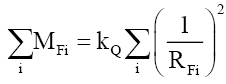 (44)
(44)
• That is, (44) is the conservation of the particle radius RF as masses are linearly additive.
• The conservation of mass is not as fundamental as once thought, as conservation of mass-energy is based on the conservation of the particle radius RF (44).
• Even though mass is probabilistic, total mass is definite, just as total probability must equal 1.
• Contracting the radius RM increases mass by increasing the probabilistic intensity per (27) and (40).
• There are two types of mass-based interactions.
• External to the particle radius: Examples are electron-electron, electron-proton, and proton-proton interactions.
• Internal to the particle radius: Within the confines of the particle radius RM the probabilistic density envelope function φM converts probabilistic intensity into probabilistic mass. Therefore, one infers that in the absence of electric or magnetic fields, mass-based particle interactions require mass interactions at a probabilistic level. Therefore, one can propose that neutrinos have low interaction with mass-based matter as their probabilistic mass is spread over a disc area that is 1,647 larger than the proton’s.
• Neutrino: The neutrino’s probability of localization is bound by neutrino’s radius Rν and therefore, per 8.b, neutrino interaction with matter is due to its mass Probabilistic Wave Function ψM.
This model (43) is much simpler than the Higgs Field model, and has the advantage that it is not dependent upon the external properties of the spacetime in which the particle exists, i.e. it is self-contained.
Fundamental, Composite and Compound Particles
Addressing (41) and (42). When a particle PM of radius RM consists of a fundamental particle PF with radius RF and a delta particle PΔ with radius RΔ the resulting particle radius is derived from the sum of the sizes of the two mass intensity discs,
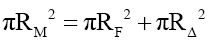 (45)
(45)
or using the up and down quarks as examples, respectively,
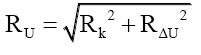 (46)
(46)
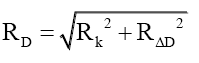 (47)
(47)
Solving for (41) and (42) gives an error of -0.069% and -0.275%, respectively. That (46) and (47) are correct, and therefore, one can define a composite particle PC of mass MC and radius RC, as one consisting of a fundamental particle PF with and a delta particle PΔ,
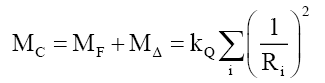 (48)
(48)
Whose radius per (49) is,
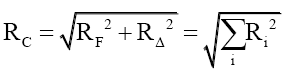 (49)
(49)
Therefore, quarks are composite particles. In addition, one can propose compound particles (for example nucleons) which consists of at least one composite particle (38), (44) and (47) are a means to distinguishing composite particles from fundamental particles. One can then propose, within the limits of this data, that Mk (MeV) must obey some kind of internal model for fundamental particles PF,
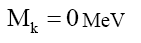 (50)
(50)
And for composite particles,
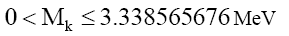 (51)
(51)
Bound Photons as the Origin of Mass
In particle processes, mass converts instantaneously into non-mass photon energy as one of the reaction outcomes, therefore, this mass intensity has electromagnetic properties. The simplest extrapolation (per Occam’s Razor) of this electromagnetic property inference, is that mass MF is derived from nF photons bound within the particle radius RM, such that, using (35) when Mk=0, and substituting for the mass equivalent of photon energy EP of a single bound photon whose wavelength λP is the de Broglie wavelength λF of the mass particle (51),
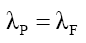 (52)
(52)
Using the mass equivalent of the photon energy,
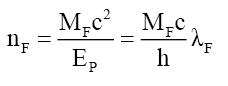 (53)
(53)
From the de Broglie (23)
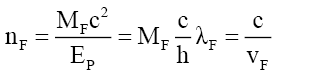 (54)
(54)
That the number of bound photons is purely a function of the velocity VF of the mass particle. Some particles, like quarks, consists of 2 sets, nF and nk, of bound photons, while fundamental particles like e, ν, Pk, PΔU, and PΔD, consist of only 1 set of nF bound photons. Note, both sets of bound photons travel at the same velocity VF as both are within the same composite particle,
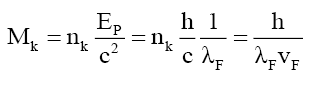 (55)
(55)
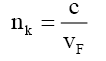 (56)
(56)
and,
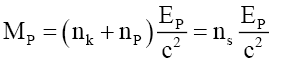 (57)
(57)
That is, mass is quantized ns in a variable form governed by λF. (40) explains why mass-based particles and photons have the same wave-particle behavior. Interestingly enough, (54) and (56) show that as a mass based particle approach the velocity of light it turns into a photon as the number of bound photons approaches 1.
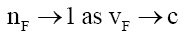 (58)
(58)
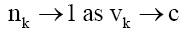 (59)
(59)
The two inferences from (58) and (59) are (i) This is a possible mechanism as to the origins of cosmic gamma rays. And (ii) the reason mass based particles cannot exceed the velocity of light, as they become light photons.
Proposing the rules for bound photons within mass
The arrangement of the bound photons’ probability discs are in the same plane as that of the mass disc and their motion vectors are parallel with the mass disc’s motion vector, else any motion would cause synchrotron radiation.
Returning to (25) and (27), the refraction ηF and phase change αF of the mass wave function ψM at RF, such that the particle disc probabilistic intensity of the mass must equal that of the nF photons (for a fundamental particle, to keep it simple).
From Appendix G, the mass probability function can be stated as two sets of functions,
(i) When rM >RF because outside the particle radius RF it is the same as the photon wave function,
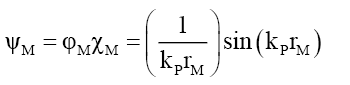 (60)
(60)
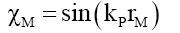 (61)
(61)
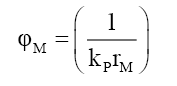 (62)
(62)
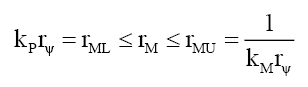 (63)
(63)
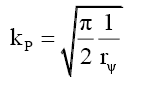 (64)
(64)
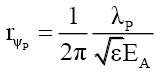 (65)
(65)
And (ii) when rM ≤RF,
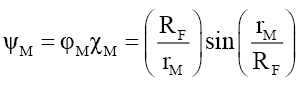 (66)
(66)
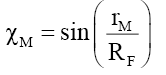 (67)
(67)
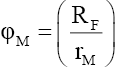 (68)
(68)
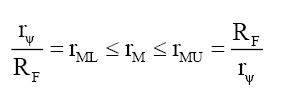 (69)
(69)
This implies, like the nucleus and compound particles whose nuclear refraction is governed by (18), that the spacetime inside fundamental particles is much “richer” and different from that of spacetime in free space. At the edge of the particle radius rM=RF the wave function refraction ηF and phase change αF can be determined from (58) and (63),
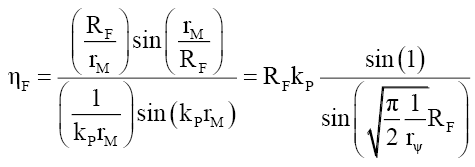 (70)
(70)
Since sin (1) is a constant,
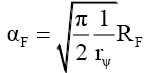 (71)
(71)
Returning to (54) one can propose that the internal tangential velocity Vn,t of nF bound photons is the un-refracted velocity Vn,t, such that the refracted velocity is the velocity of mass VF or,
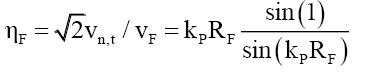 (72)
(72)
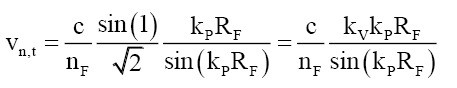 (73)
(73)
The physical interpretation of (73) is that the bound photons are rotating within the mass disc at the velocity Vt,x and Vt,y in the x-y plane, noting that the bound photon discs are in the plane of the mass disc. That is, the nF bound photons are not static but dynamic rotating structures with tangential velocities to the transverse wave propagation that slows their motion to that of the particle VF in the z-axis, such that the net velocity is given by the vector sum of the photon velocity and the rotational velocities.
This will be presented in a future paper.
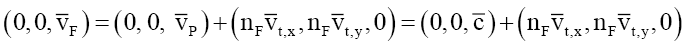 (74)
(74)
Noting that the radial velocities cancel out leaving a particle velocity vF in the direction of motion. Due to the nF multiplication the x- and y- velocity components increase substantially compared to the velocity of light c producing a net slowing of the particle velocity, but more research is required here.
Returning to (60), the total mass probability density DψM G (19) of the mass disc within the particle radius RF is given by,
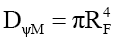 (75)
(75)
And the total photon probability density DψP D (19) is,
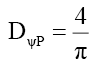 (76)
(76)
Assuming that probability densities are additive, by (57) the total mass probability density DψM should be a multiple of the total photon probability density DψP, such that,
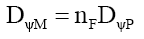 (77)
(77)
Or,
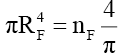 (78)
(78)
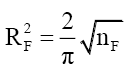 (79)
(79)
Using (43)
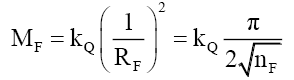 (80)
(80)
(79) contradicts (57).
Rule 1: One infers that even though mass and energy are additive, probability densities are not. Therefore, combining probability density functions is a much more sophisticated process. This provides some guidance as to how photons are or are not bound with this mass probability density function. Returning to (75), using (43),
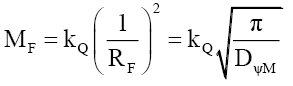 (81)
(81)
Or
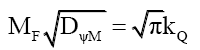 (82)
(82)
Rule 2: The relationship between mass MF and its total mass probability density DψM is hyperbolic, and interchangeable as governed by (82). Rewriting, gives,
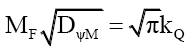 (83)
(83)
That is, the particle’s mass-energy transforms between energy and probability density, much like kinetic energy and potential energy, except this relationship is hyperbolic. This process explains how the number ηF of bound photons reduces as the mass particle increases in velocity (58) and (59). (84) to ((87) illustrates this 3-step process for nF bound photons of frequency νn dropping to nF-1 bound photons of frequency νn-1 as velocity increases,
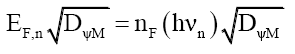 (84)
(84)
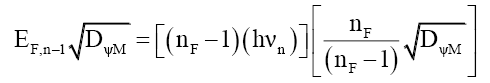 (85)
(85)
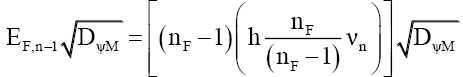 (86)
(86)
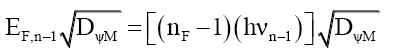 (87)
(87)
Using the summative properties of mass MFi (44) of i particles with total mass probability density DψMi,
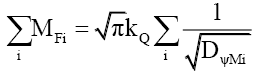 (88)
(88)
Rule 3: The net mass probability density DψM of a non-fundamental particle, consisting of i particles each with a total mass probability density DψMi, is given by,
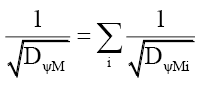 (89)
(89)
By (76) the photon’s total disc probability density DψP is a constant 4/π, and therefore independent of the photon energy. This is very different from the properties of the mass probability density.
Rule 4: One infers that the binding of ηF photons to form mass MF introduces a binding transformation ∇B such that,
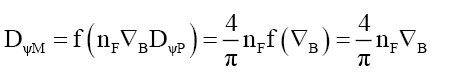 (90)
(90)
As for a given velocity ηF is a constant and from (75) so is DψP. From (74),
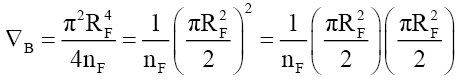 (91)
(91)
That is, the transformation process is a function of half the area of the mass disc. One inference is that as the electric and magnetic super vectors rotate between space time and subspace, half the area circumscribed these super vectors is in spacetime and the other half is in subspace, but more research is required.
Consequences of the new matter-gravity relationship
What is the matter-gravity relationship?: Equations (11) to (18) determine how matter creates the gravitational field. By altering spacetime at the RMS charge radius ri,c and the step-down velocity vs,r, spreads radially throughout spacetime, from ri=ri,c to ri=∞, as governed by equation (16). This velocity vs,r, is a measure and determinant of the transformations present in spacetime.
Unknown systematic error
One can now propose that systematic errors are present in all near field gravitation probe experiments. This is due to variations in the isotopic gravitational constant Gi, per the material used to cause variations in the gravitational force. Specifically, when Gi>GE the variations in gravitational force will be greater and vice versa. It would also be necessary to predetermine the composite gravitational constant GC, of the test materials and surrounding location due to local differences in the isotopic composition at that part of the Earth’s crust. Note that the aggregation constant ka, R can still introduce systematic errors if test materials are of different material compositions.
Gravitational constant G is a variable
The gravitational constant G, is correctly a variable Gi, equation (12). The hyperbolic relationship, equation (12), between Gi and Mi explains why Earth based gravitational constant GE has only been observed as a constant.
Mass is a proxy for matter
Note that, for a single nucleus i, the gravitational mass MH is the mass of the nucleus Mi, and equation (12) reduces to,
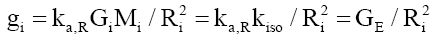 (92)
(92)
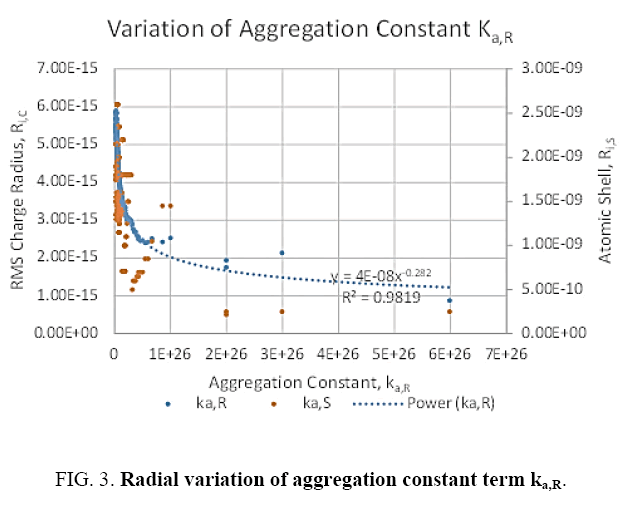
That is, for a single atom, its gravitational field acceleration is independent of the mass of the atom source. Therefore, mass is a proxy for the amount of matter. Checking equation (92) with (11) shows that the aggregation constant term is not constant over radial distances at subatomic sizes, shown in Figure 3 and equation (93),
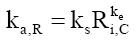 (93)
(93)
Where the slope constant ks=7.425421 × 10-26 and the exponent constant ke= -3.477708.
Therefore, when aggregating mass into a gravitating body, it is necessary to know specifically, (i) the amount (due to clustering of matter, MH), (ii) the type (due to Gi), and (iii) the arrangement (due to ka,R) of matter causing the gravitational field. In effect equation (11) can be written as.
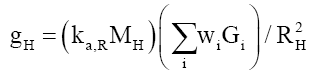 (94)
(94)
With ka,RMH the aggregating factor and Σ wi Gi the composite gravitational constant, GC.
Mass of heavenly bodies
Equation (94) shows that the measured mass of the heavenly bodies will be dependent upon the isotopic composition of their matter.
For example, Earth composition of 35.0% Fe, 30.0% O, 15.0% Si, 13.0% Mg, 2.4% Ni, 1.9% S, 1.1% Ca, 1.15% Al, and 0.5% others, gives a weighted average gravitational constant of 6.673840 × 10-11.
For illustration purposes, one can determine Jupiter’s mass is 22.6 times less at 8.391321 × 10+25 kg instead of the current estimate of 1.900 × 10+27 kg. This was arrived at by using
• Ihe value of the aggregation constant ka,R provided in equation (94);
• Isotopic gravitational constants of Hydrogen (1H) and Helium (4He) of 1.777957 × 10-09 and 4.441839 × 10-10, respectively;
• Jupiter consists of 80% hydrogen and 20% helium; iv) giving a composite gravitational constant GJ=1.511120 × 10-09 for Jupiter. Note, here one is assuming that the aggregation constant ka,R on Earth is the same as that of Jupiter’s, but this is most likely incorrect as the Earth is predominantly Fe, O, and Si, while Jupiter is predominantly H. Thus, the determination of the true mass of a heavenly body will be dependent upon its isotopic composition.
Proton Radius Puzzle
Pohl [20] reported measurement of the Lamb shift in the exotic muonic hydrogen atom yielded a proton charge radius RM of 0.84087(39) fm, which is 4.17% smaller than the electron hydrogen atom proton size of 0.8775 (61) fm [21]. Substituting these values into the mass model (38) a sTable Mk of 938.2714 MeV compared to the proton mass of 938.2721 MeV, and the respective electron and muon proton MΔe and MΔμ have masses of 6.282812 × 10-04 MeV and 6.842119 × 10-04 MeV. That is, in the presence of a muonic atomic shell the proton has gained a little mass-energy on the order of 60 part per billion, and possibly not detected or looked for in these proton size puzzle experiments.
Conclusion
This paper has shown that
• the source of gravitational fields is due to quark motion.
• that mass is probabilistic and based on bound photons within the particle radius, in such a manner as to be consistent with the de Broglie wave function and
• that together producing conservation of mass energy that is derived from particle size.
That is, many disparate physical phenomena come together in a more consistent manner, without adding to either the known or unknown Universe. This is meant to complement the usual quark contributions to nuclear physics which can be seen in [22,23].
References
- Efstathiou G, Pryke C, Steinhardt P, et al. Spotlight live: Looking back in time-oldest light in existence offers insight into the universe”. Kavli Foundation; 2015.
- Nemiroff RJ, Connolly R, Holmes J, et al. Bounds on spectral dispersion from fermi-detected gamma ray bursts. Phys Rev Lett. 2012;108(23):231103.
- Solomon BT. New evidence, conditions, instruements and experiments for gravitational theories. J Mod Phys. 2013;4(8A):14.
- Solomon BT. Non-Gaussian photon probability distributions, in the proceedings of the space, propulsion and energy sciences international forum (SPESIF-10). Robertson GA, editor. AIP conference proceedings 1208, Melville, New York; 2010.
- Solomon BT. Super physics for super technologies: Replacing Bohr, Heisenberg, Schrödinger and Einstein. Propulsion Physics Inc Denver; 2015.
- Bondi H. Negative mass in general relativity. Rev ModPhy. 1957;29(3):423.
- Klein M. Mathematics: The loss of certainty, Oxford University Press; 1982.
- Solomon BT. An introduction to gravity modification: A guide to using Laithwaite's and Podkletnov's experiments and the physics of forces for empirical results. Universal-Publishers; 2012.
- Solomon BT. Gravitational acceleration without mass and non-inertia fields. Phys Ess. 2011;24(3):327-37.
- Solomon BT. Non-Gaussian photon probability distributions, in the proceedings of the space, propulsion and energy sciences international forum (SPESIF-10). Robertson GA, editor. AIP conference proceedings 1103, Melville, New York; 2010.
- Hooft G. A locally finite model for gravity. Found physics. 2008;38:733-57.
- Cowen R. Quantum method closes in on gravitational constant: Cold rubidium atoms provide fresh approach to measuring Newton's big G. Nature; 2014.
- Conversation with Beckwith A, Department of Physics, Chongqing University, China.
- Feynman R. Feynman lectures on Physics; 2010. 28-4c.
- Solomon BT. “Photon probability control”. Proceeding of the SPIE 2016 photonics west conference and exhibition, San Francisco; 2016.
- Solomon BT, Beckwith AW. Photon probability control with experiments. J Space Explor. 2016;6(1).
- Solomon BT, Beckwith AW. Probability,randomness,and subspace with experiments. J Space Explor. 2016;6(1).
- Pohl R. Laser spectroscopy of muonic atoms and ions. Frontiers in Optics/Laser Science; 2015.
- Pohl R, Nez F, Udem T, et al. Deuteron charge radius from spectroscopy data in atomic deuterium. physics.atom-ph: 2016.
- Libertexts.org [internet]. Case study: The natural abundance of elements [cited 2017 Jan 22]. Available from: http://chemwiki.ucdavis.edu/Inorganic_Chemistry/Case_Studies/Case_Study%3A_The_Natural_Abundance_of_Elements
- Astronomytoday.com [internet]. Jupiter, the largest planet, Astronomy Today [cited 2017 Jan 22]. Available from: http://www.astronomytoday.com/astronomy/jupiter.html.
- Amsler C.Review of particle physics. Phy Lett B. 2008;667:1-5.
- Hendry AW, Lichtenberg DB. “Properties of Hadrons in the Quark Model. Fortschritte der Physik. 1985;33(3):139-231.