Original Article
, Volume: 15( 4)Strongly Prime ï -Semigroup
- *Correspondence:
- Jyothi V Department of Mathematics, KL University, Guntur, Andhra Pradesh, India Tel: 0863-2399999 E-mail: jyothi.mindspace@gmail.com
Received: September 08, 2017; Accepted: October 23, 2017; Published: October 25, 2017
Citation: Jyothi V, Sarala Y, Madhusudhana Rao D, et al. Strongly Prime  -Semigroup. Int J Chem Sci. 2017;15(4):206
-Semigroup. Int J Chem Sci. 2017;15(4):206
Abstract
The paper introduces the concepts of β-insulator and strongly prime-semigroups. Several characterizations of them are furnished.
Keywords
β Insulator; Strongly prime; Right and left α-annihilator
Introduction
The idea of general semigroups was developed by Anjaneyulu [1]. Saha defined  -semigroup as a generalization of
semigroup as follows. Various kinds of
-semigroup as a generalization of
semigroup as follows. Various kinds of  -semigroups have been widely studied by many authors [2-6].
-semigroups have been widely studied by many authors [2-6].
this paper we introduce and study the structure of β-insulator and strongly prime  -semigroups. In this paper many
important results of strongly prime ideals in semigroups have been extended to strongly prime ideals in
-semigroups. In this paper many
important results of strongly prime ideals in semigroups have been extended to strongly prime ideals in  -semigroups.
-semigroups.
Prime and semiprime ideals of  -semigroups
-semigroups
Definition 1.1: A subset A of a  -semigroup S is said to be an m–system if
-semigroup S is said to be an m–system if 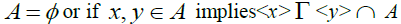
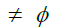
Definition 1.2: A subset A of a  -semigroup S is said to be an n – system if
-semigroup S is said to be an n – system if 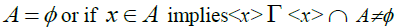
Lemma 1.3: Let S be a  -semigroup. An ideal A in S is semiprime if and only if AC is an n – system.
-semigroup. An ideal A in S is semiprime if and only if AC is an n – system.
Proof: Suppose that A is a semiprime ideal and let 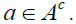 Then
Then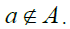 Since A is semiprime
Since A is semiprime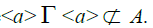 It implies
that
It implies
that 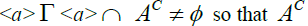 is an n – system.
is an n – system.
Conversely, suppose 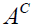 is an n – system and let
is an n – system and let 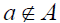 . We shall prove that
. We shall prove that 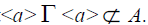 Since
Since 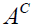 is an n – system. <a>
is an n – system. <a>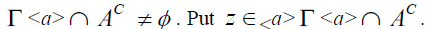 So that
So that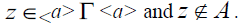 Hence
Hence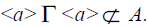 Thus, A is a
semiprime ideal.
Thus, A is a
semiprime ideal.
Definition 1.4: For any ideal Q of a  -semigroup S, we define n (Q) to the set of elements x such that every n – system
containing x of S contains an element of Q.
-semigroup S, we define n (Q) to the set of elements x such that every n – system
containing x of S contains an element of Q.
Definition 1.5: An ideal Q in a -semigroup S is said to be right primary if for any ideal U and V, U
-semigroup S is said to be right primary if for any ideal U and V, U  V implies U ⊆ m
(Q) or V ⊆ Q.
V implies U ⊆ m
(Q) or V ⊆ Q.
Theorem 1.6: Let S be a  -semigroup for any right primary ideal P in S, the following are equivalent
-semigroup for any right primary ideal P in S, the following are equivalent
(i) P is a prime ideal.
(ii) P=n (P).
(iii) P is a semiprime ideal.
Proof: (i) ⇒(ii) Let P be a prime ideal then P ⊆ n (P) is obvious. On the other hand, let x ∈ n (P) and suppose that x ∉P.
Since P is prime, PC is an m-system and x∈ PC . Then there exists an n-system N ⊆ PC such that x ∈N. But N is disjoint from P , therefore x∉ n (P), which is a contradiction. Hence x ∈P, so that n (P) ⊆ P
(ii) ⇒ (iii) is obvious.
(iii) ⇒ (i) Suppose that P is a semiprime ideal. We have to prove that P is a prime ideal. Let U and V be any ideal in S
with 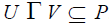 . Since P is primary,
. Since P is primary, 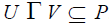 implies that
implies that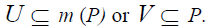 Since P is a semiprime ideal, P =
m (P). Hence, U ⊆P or V ⊆ P. Thus P is a prime ideal in S.
Since P is a semiprime ideal, P =
m (P). Hence, U ⊆P or V ⊆ P. Thus P is a prime ideal in S.
Theorem 1.7: For any ideal P in S, P is prime if and only if P is primary and semiprime.
Proof: Suppose that P is a prime ideal. We have to prove that P is primary. Let U and V be any ideal in S such that U  V ⊆ P. Since P is a prime ideal, U ⊆ n (P) or V ⊆ P by theorem 2.6. Now our claim is that n (P) ⊆ m (P). Let x ∈ n (P) and S be any m – system containing x. Since is any m – system is an n – system, S is an n – system containing x. Since x ∈ n (P), S meets P . Hence x ∈ m (P) and therefore U ⊆ n (P) or V ⊆ P implies that U ⊆ m (P) or V ⊆ P. Hence P is a primary ideal. Since every prime ideal is a semiprime ideal, P is semiprime and hence primary ideal.
V ⊆ P. Since P is a prime ideal, U ⊆ n (P) or V ⊆ P by theorem 2.6. Now our claim is that n (P) ⊆ m (P). Let x ∈ n (P) and S be any m – system containing x. Since is any m – system is an n – system, S is an n – system containing x. Since x ∈ n (P), S meets P . Hence x ∈ m (P) and therefore U ⊆ n (P) or V ⊆ P implies that U ⊆ m (P) or V ⊆ P. Hence P is a primary ideal. Since every prime ideal is a semiprime ideal, P is semiprime and hence primary ideal.
Conversely, suppose that P is primary and semiprime ideal. By theorem 1.6, P is a prime ideal.
Strongly prime  -semigroups
-semigroups
Definition 2.1: Let S be a  -semigroup. Let S is said to be semiprime if 0 is a semiprime ideal. S is said to be prime if
(0) is a prime ideal.
-semigroup. Let S is said to be semiprime if 0 is a semiprime ideal. S is said to be prime if
(0) is a prime ideal.
Definition 2.2: Let S be a  -semigroup. If A is a subset of S, we defined a right α -annihilator of A to be a right ideal
-semigroup. If A is a subset of S, we defined a right α -annihilator of A to be a right ideal 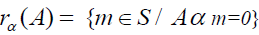
Definition 2.3: Let S be a  -semigroup. If A is a subset of S, we defined a left α-annihilator of A to be a left ideal
-semigroup. If A is a subset of S, we defined a left α-annihilator of A to be a left ideal 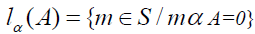
We adopt the symbol S* to denote the nonzero element of S.
Definition 2.4: A right β -insulator for a ∈ S* is a finite subset of S, Mβ(a) such that 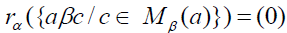 , for all
, for all
Definition 2.5: A left β -insulator for a∈S* is a finite subset of S, Mβ(a) such that 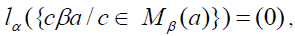 for all
for all 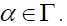
Definition 2.6: A  -semigroup S is sad to be a right strongly prime if for every
-semigroup S is sad to be a right strongly prime if for every 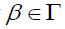 , each non zero element of S, has a
right β -insulator, that is for every
, each non zero element of S, has a
right β -insulator, that is for every 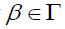 and a∈S* , there is a finite subsest Mβ(a) such that for
and a∈S* , there is a finite subsest Mβ(a) such that for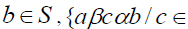
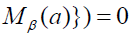 , for all α∈
, for all α∈ implies b =0.
implies b =0.
Definition 2.7: A  -semigroup S is sad to be a left strongly prime if for every
-semigroup S is sad to be a left strongly prime if for every 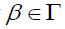 , each non zero element of S, has a left
β -insulator, that is for every
, each non zero element of S, has a left
β -insulator, that is for every 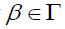 and a∈S* , there is a finite subsest Mβ(a) such that for
and a∈S* , there is a finite subsest Mβ(a) such that for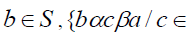
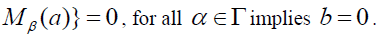
Definition 2.8: A  -semigroup S is sad to be a left weakly semiprime
-semigroup S is sad to be a left weakly semiprime  -semigroup if
-semigroup if 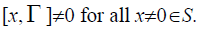
Definition 2.9: A  -semigroup S is sad to be a right weakly semiprime
-semigroup S is sad to be a right weakly semiprime  -semigroup if
-semigroup if 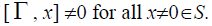
Definition 2.10: A  -semigroup S is sad to be a weakly semiprime
-semigroup S is sad to be a weakly semiprime  -semigroup if it is both left and right weakly
semiprime.
-semigroup if it is both left and right weakly
semiprime.
Theorem 2.11: Let S be a  -semigroup with D.C.C on annihilators then S is prime if S is strongly prime.
-semigroup with D.C.C on annihilators then S is prime if S is strongly prime.
Proof: Suppose that S is right strongly prime. To prove S is prime, let 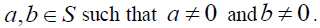 Since S is right
strongly prime, for every
Since S is right
strongly prime, for every 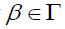 , there exists a right β-insulator Mβ(a) for a. Then
, there exists a right β-insulator Mβ(a) for a. Then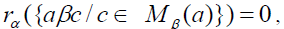
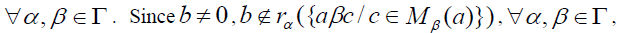 there exists
there exists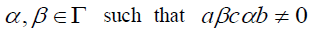 where
where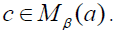 Hence S is prime.
Hence S is prime.
Conversely, suppose that S is prime. We have to prove that S is right strongly prime. Let 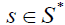 and consider the collection
of right α-annihilator ideals of the form
and consider the collection
of right α-annihilator ideals of the form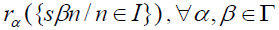 where I run over all finite subsets of S containing
the identity. Since S satisfies the d.c.c. on right annihilators, choose a minimal element K. If
where I run over all finite subsets of S containing
the identity. Since S satisfies the d.c.c. on right annihilators, choose a minimal element K. If 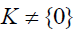 we can find an element
we can find an element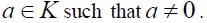 Since S is a prime
Since S is a prime  -semigroup, it follows from 2.6 theorem, that there exists b∈S
-semigroup, it follows from 2.6 theorem, that there exists b∈S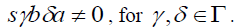
Let 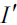 be a finite subset of S containing the identity and b. Since,
be a finite subset of S containing the identity and b. Since, 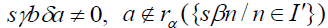 , a contradiction.
This forces that
, a contradiction.
This forces that 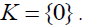 Thus, s has a right β-insulator
Thus, s has a right β-insulator 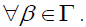 Since
Since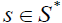 is arbitrary, every element of
is arbitrary, every element of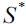 has a right
β-insulator
has a right
β-insulator 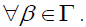 Similarly, every element of
Similarly, every element of 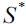 has a left β-insulator
has a left β-insulator 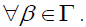 Hence S is a strongly prime
Hence S is a strongly prime  -
semigroup.
-
semigroup.
Definition 2.12: Let S be a  -semigroup. A left ideal I of S is said to be essential if
-semigroup. A left ideal I of S is said to be essential if 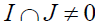 for all nonzero left ideals J
of S.
for all nonzero left ideals J
of S.
Definition 2.13: The singular ideal of a  -semigroup S is the ideal composed of elements whose right α-annihilator for each
-semigroup S is the ideal composed of elements whose right α-annihilator for each
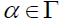 is an essential right ideal.
is an essential right ideal.
Theorem 2.14: If S is a strongly prime  -semigroup having no zero devisor, then singular ideal is zero.
-semigroup having no zero devisor, then singular ideal is zero.
Proof: Let S is a strongly prime  -semigroup and A be a singular ideal. Suppose that there exists an element
-semigroup and A be a singular ideal. Suppose that there exists an element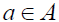 such that
such that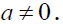 Let Mβ(a) be a right β -insulator for a. Since A is an ideal,
Let Mβ(a) be a right β -insulator for a. Since A is an ideal, 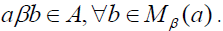 Now
Now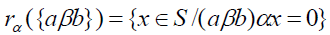 implies that
implies that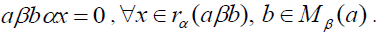 Then aβbα
Then aβbα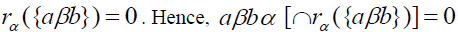 . Since A is singular,
. Since A is singular, 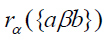 is essential for all
is essential for all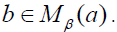 We know that the intersection of finitely many essential right ideals is nonzero. Since Mβ(a) is finite,
We know that the intersection of finitely many essential right ideals is nonzero. Since Mβ(a) is finite,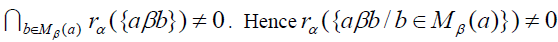 , which is a contradiction to the β -insulator Mβ(a) Consequently A=0.
, which is a contradiction to the β -insulator Mβ(a) Consequently A=0.
Definition 2.15: Let S be a  -semigroup. Let us define a relation
-semigroup. Let us define a relation 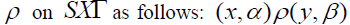 if and only if
if and only if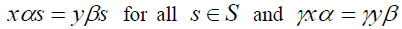 for all
for all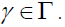 Then ρ is an equivalence relation. Let [x, α ] denote the equivalence class containing
Then ρ is an equivalence relation. Let [x, α ] denote the equivalence class containing 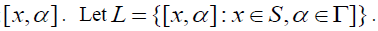 Then L is a semigroup with respect to the
multiplication defined by
Then L is a semigroup with respect to the
multiplication defined by 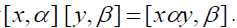 This semigroup L is called the left operator semigroup of the
This semigroup L is called the left operator semigroup of the  -
semigroup.
-
semigroup.
Theorem 2.16: If S is a right strongly prime  -semigroup, then the left operator
-semigroup, then the left operator  -semigroup L(R) is right strongly prime
-semigroup L(R) is right strongly prime
 -semigroup.
-semigroup.
Proof: Suppose that S is right strongly prime  -semigroup. To prove L is right strongly prime
-semigroup. To prove L is right strongly prime  -semigroup, it is enough to
prove that every nonzero element in L has a right insulator. Let
-semigroup, it is enough to
prove that every nonzero element in L has a right insulator. Let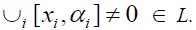 Then there exists
Then there exists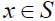 such that
such that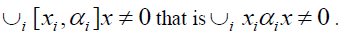 Since S is right strongly prime, for every
Since S is right strongly prime, for every 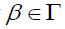 , there exist an β-insulator for ∪i
, there exist an β-insulator for ∪i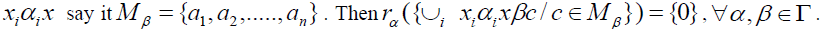 Hence for any
Hence for any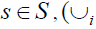
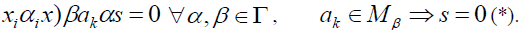 Now fix
Now fix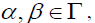 consider the collection
consider the collection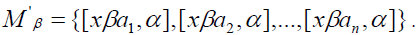 We shall prove that
We shall prove that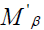 is an insulator for
is an insulator for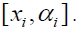 It is enough to prove that
It is enough to prove that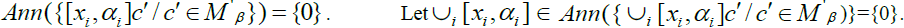 Then
Then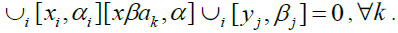 We claim that
We claim that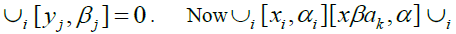
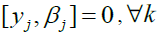 implies that
implies that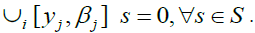 Therefore
Therefore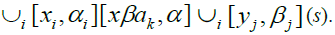
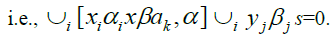
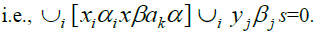
By 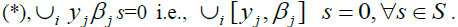 Hence,
Hence,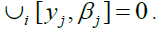 Since
Since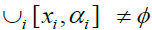 is arbitrary,
every nonzero element in L has a right β -insulator. Similarly, if S is left strongly prime, then every non-zero element of R
has a left β -insulator. Thus, L is right strongly prime, and R is a left strongly prime
is arbitrary,
every nonzero element in L has a right β -insulator. Similarly, if S is left strongly prime, then every non-zero element of R
has a left β -insulator. Thus, L is right strongly prime, and R is a left strongly prime  -semigroup.
-semigroup.
Theorem 2.17: A  -semigroup S is weakly semiprime then S is strongly prime and only if its left operator semigroup L is
right strongly prime and its right operator semigroup R is left strongly prime.
-semigroup S is weakly semiprime then S is strongly prime and only if its left operator semigroup L is
right strongly prime and its right operator semigroup R is left strongly prime.
Proof: Suppose that L is a right strongly prime  -semigroup. In order to prove that S is a strongly prime
-semigroup. In order to prove that S is a strongly prime  -semigroup, we
shall prove that for every
-semigroup, we
shall prove that for every 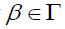 , every non-zero element in S has a right β -insulator. Let
, every non-zero element in S has a right β -insulator. Let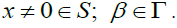 Since S is a
left weakly semiprime
Since S is a
left weakly semiprime -semigroup,
-semigroup, 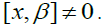 Since L is right strongly prime, there exists a right insulator
Since L is right strongly prime, there exists a right insulator 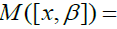
 Therefore, for any
Therefore, for any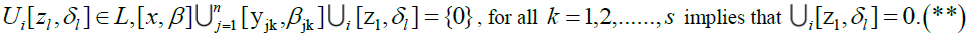 Consider
Consider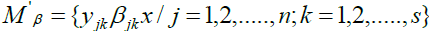 . We now claim that
. We now claim that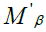 is a β -insulator for x. It is enough to
prove that for each. Let
is a β -insulator for x. It is enough to
prove that for each. Let 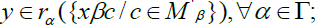 then
then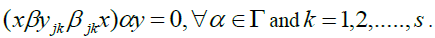 Therefore
Therefore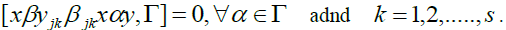 Hence
Hence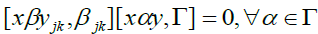 and
and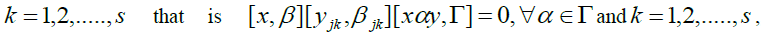 so that
so that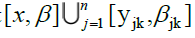
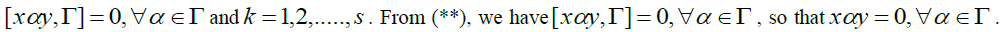 Since
S is faithful L \ R bimodule, we have y=0. Since
Since
S is faithful L \ R bimodule, we have y=0. Since 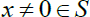 is arbitrary, for every
is arbitrary, for every 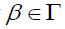 , every non-zero element in S has
a right β -insulator. Hence S is a right strongly prime
, every non-zero element in S has
a right β -insulator. Hence S is a right strongly prime  -semigroup. Similarly, if R is a left strongly prime
-semigroup. Similarly, if R is a left strongly prime  -semigroup
then S is a left strongly prime
-semigroup
then S is a left strongly prime  -semigroup. Converse part follows from Theorem 2.16.
-semigroup. Converse part follows from Theorem 2.16.
Proposition 2.18: If S is strongly prime  -semigroup, then S is weakly semiprime
-semigroup, then S is weakly semiprime  -semigroup.
-semigroup.
Proof: Suppose that S is strongly prime  -semigroup. We shall prove that S is a weakly semiprime
-semigroup. We shall prove that S is a weakly semiprime  -semigroup. Let
-semigroup. Let 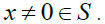 It is enough to prove that
It is enough to prove that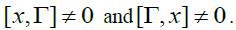 Suppose that
Suppose that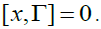 Since S is a strongly prime
Since S is a strongly prime  - semigroup, for every
- semigroup, for every 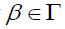 there exists a finite subset
there exists a finite subset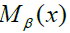 such that for
such that for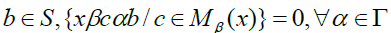 implies that
implies that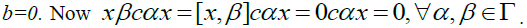 Hence x=0, a contradiction. Thus, S is a weakly
semiprime
Hence x=0, a contradiction. Thus, S is a weakly
semiprime  -semigroup.
-semigroup.
References
- Anjaneyulu A. Semigroups in which prime ideals are maximal. Semigroup forum. 1981;22:151-8.
- Aiyared I. Note on Bi-ideals in-semigroups. Int J Algebra. 2009;3(40):181-8.
- Clifford AH, Preston GB. The algebraic theory of semigroups. Am Mathematical Soc. Provience. 1967.
- Sen MK, Saha NK. On semigroups-I. Bulletin of Calcutta Mathematical Soc. 1986;78:180-6.
- Sen MK, Saha NK. On-semigroups-II. Bulletin of Calcutta mathematical Soc. 1987;79:331-5.
- Kyuno S. On prime-rings. Pacific J Math. 1978;75(1):185-90.
