Original Article
, Volume: 16( 1)Observation of Acoustic Impedance of Solid and Reflected Angles to Porous Ti-Mn Alloys Via Analysis Description by Scanning Acoustic Modes
- *Correspondence:
- Yahya Al-Sayad, Laboratory of Semi-Conductors, Department of Physics, Faculty of Sciences, Badji-Mokhtar University, BP 12, Annaba, DZ-23000, Algeria, Tel: +213559405898; E-mail: yahya_sayaad@yahoo.com
Received: November 23, 2017; Accepted: December 26, 2017; Published: January 03, 2018
Citation: Yahya Al-Sayad*, Abdellaziz Doghmane and Zahia Hadjoub. Observation of Acoustic Impedance of Solid and Reflected Angles to Porous Ti-Mn Alloys Via Analysis Description by Scanning Acoustic Modes. Int J Chem Sci. 2018;16(1):234
Abstract
Ti-Mn alloy with crystal structure having a Poisson’s ratio of 0.33 and density around (4730) gcm-3, Ti-Mn alloy was prepared by mechanical alloying for many applications. In the present study, effect of porous Ti and TixMn (with x=5) alloy with different porosities (21%, 40.53% and 56%) were applied. It was found that as the porous TixMn alloys increases from (21% to 56%) with increasing Acoustic parameter values of propagating of solid Acoustic impedance (ZL, ZT, Z Solid) and longitudinal, transverse and Rayleigh reflected angles (ƟL, ƟT, ƟR) are as follows : ZL (3311-4029) MrayI, ZT (1668-2030) MrayI, ZSolid (35-51.83) MrayI and ƟL (13.16 19.19 dag., ƟT (34.3-50.8)dag., ƟR (38.77-41.63) dag respectively, using some acceptable physical approximations were used. ZT impedance and ZL impedance dependence on porosities of material studied, behavior cases showed due to different propagating wave modes in the surface, features at some critical angles at which longitudinal, shear and Rayleigh modes are generated. Such change influence Acoustic impedance on porous Ti-Mn alloys Acoustic signature.
Keywords
Ti-Mn structure; Acoustic impedance; Porosity; Acoustic parameters; Porous
Introduction
Ti-Mn alloys have generally important using in available range of products for hydrogen storage research, advanced fuel cells, dental implants and battery applications. Because of their exceptional mechanical properties and corrosion resistance compared to the more conventional stainless steel and cobalt-based alloy [1]. Its elastic modulus and Acoustic impedance is widely used as mechanical property of solid materials as well as how orientation of atoms in materials, so that their use would help realize to the reflection angles of longitudinal transverse and Rayleigh [2-4]. However, there are some mechanical properties as Young’s modulus, for Ti alloys is varying from 110 to 55 GPa [5]. Ti-Mn alloy was prepared by mechanical alloying and subsequently consolidated by spark plasma sintering (SPS) technique [6], could be the use of porous materials in stems. There have been a number of previous reviews on the many different porous Titanium could be produced by various methods as powder metallurgy process, (EBM) process and (HIP) to reduce porosity, porous matrices that have been developed [7].
This report study: characterize the materials, Acoustic phenomena characterization get Acoustic images can be cleared understanding of the physical mechanisms of their formation and the nature of Acoustic contrast. Knowledge of these mechanisms allows one to make quantitative and quantitatively measurements, characterize the materials studied. Measuring the output signal of an Acoustic microscope, one obtains information about the speed of sound, Acoustic impedance and geometric characteristics of the slope angle of the surface. Acoustic impedance of a Ti-Mn alloy is the product of the density (ρ) and the speed (V) of sound in that material.
The extent to which ultrasonic energy is transmitted or reflected at an interface separating two continuous isotropic materials are determined by the ratio of the characteristic Acoustic impedances of the material, energy is transmitted into the second layer and the less is reflected from the interface. Ultrasonic waves are reflected angles (?R) at surface in Ti-Mn alloy where there are differences in Acoustic impedances (Z) of Ti-Mn alloy on each side of the layers the amplitudes of the reflected and transmitted waves are controlled by the impedance ratio of the two layers and same behavior is observed with light and other waves. The reflected waves can interfere with incident waves [8-13].
Materials and Methods
Materials
Powder and mixture of Ti with 5 wt% Mn powders were wet milled in n-hexane by a planetary ball milling system. Weight ratio of ball to powder of 15:1 and rotation rate of 300 r/m. Ti5Mn powder was milled for 60 h, Ti5Mn powders were mixed with 15 wt% of (NH4HCO3), which was used as the space-holder material and 2 wt% of TiH2 powder as the pore forming [14]. Designed to consolidation, the powder was poured into a graphite die tools. It was moved into a SPS technique, were warmed to temperature at a heating rate of 100°C/min under a vacuum, Ti5Mn alloys sintered at different temperatures from 95°C to 110°C and pressure less condition [15]. The sintered Ti5Mn alloy were typically disks of 20 mm in diameter and about 5 mm in height. The porosity of the sintered Ti5Mn alloy was determined Ti-Mn alloy shows decreased porosity from 56% to 21% at elastic modulus is increased from 35 GPa to 51.83 GPa Melodramatically [16].
Methods
There are many techniques for study surface measurement obtains an image and information of the surface as X-ray radiography, SEM, STM and others. But in this study, we work by the scanning Acoustic microscope (SAM), (SAM) is a surface measurement system that looks at the reflected image from the surface of the sample. This technique can also yield information about the elastic properties of the material [17].
In this study dynamic to measure elastic properties of Ti5Mn alloys, SAM calculating process is created on the scanning Acoustic microscopy, SAM, technique effective situations of SAM below the conditions: half lens opening angle θ lens n=50°, a frequency f=140 (MHz) and coupling liquids Freon whose densities, ρ=1570 kg/m3 and longitudinal velocity of liquid VL=716 (m/s) and non-transvers velocity of liquid VS. [18], whoever, its mechanical properties of Ti5Mn alloys studied at no actual effect porosity are density, ρ=4500 (kg/m3) and Poisson ratio, ν=0.32 and Young’s modulus, E=95 (GPa) [16]. Computing reflection coefficients, R (θ) and impedance Acoustic Z for each (Freon/Ti5Mn alloys) at alteration porosity (56% to 21%), where R (θ) is written by solving Acoustic angles θ, θL, θT where R (θ) that the incident to the surface where the subscripts for longitudinal, transverse and Rayleigh modes [19]. Calculation of impedance of coupling liquid Zliq. and total impedance of solids ZSolid), as we could. Elastic properties of Ti5Mn alloys depend on alteration porosity among the coupling liquids and solid conditions.
R (θ)=(Z Ti5Mn-Z Freon) (Z Ti5Mn+Z Freon) .........................................................(1)
Z (Ti5Mn)=ZL (Ti5Mn) cos2 2θL (Ti5Mn)+ZT (Ti5Mn) sin2 2θT............................(2)
VT (Ti5Mn)=√E Ti5Mn/2ρ Ti5Mn (1+σ Ti5Mn) .......................................................(3)
VL (Ti5Mn)=2 (σ Ti5Mn-1) (VT2 (Ti5Mn) / (2σ Ti5Mn-1) ......................................(4)
ZT (Ti5Mn)=ρ VT (Ti5Mn) / Cos θT (Ti5Mn) ............................................................(5)
ZL (Ti5Mn)=ρ VL (Ti5Mn) / Cos θL (Ti5Mn) ............................................................(6)
Results and Discussion
Modulus modes measurements
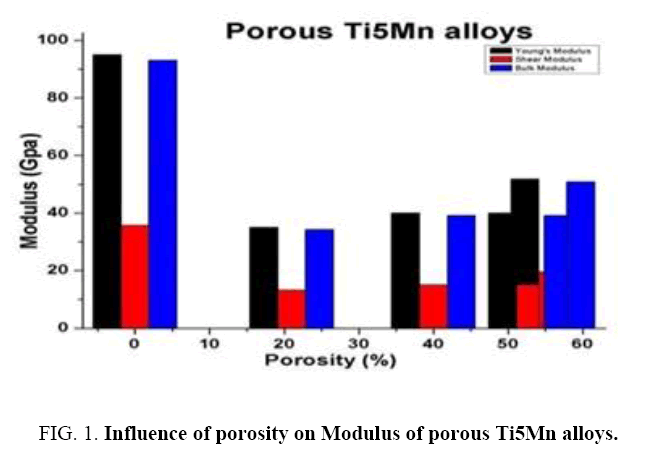
Porous Ti5Mn alloys experimental modern Young’s modulus, E was reported [16], in this work can determine the values of the shear and Bulk modulus (G and B). Making use of such results (experimental Young’s modulus and of calculation (G and B, both elastic modulus were observed with decreasing porosity P (%).
Young’s modulus of Ti5Mn alloys depends on their porosities content affected by other impact applying. They formed the Porous on Ti5Mn alloys with various porosities as cleared by Table 1. In the present we needed to find associations to the elastic modulus by porosities of Ti5Mn alloys the elastic modulus. To describe the dependence of porosities of Ti5Mn alloys on their theoretical relations have been proposed. The porosity range of the present study, there are various elastic modulus were obtained.
| Mechanical properties of Ti5Mn alloys | ||||||||
|---|---|---|---|---|---|---|---|---|
| Elastic | Experimental | Porosity | (%) | 0 | 21 | 40 | 53 | 56 |
| Density | ρ(Kgm-3) | 4500 | 4730 | |||||
| Poisson′s ratio | σ | 0.32 | 0.33 | |||||
| Young′s Modulus | E (GPa) | 95 | 35 | 40 | 40 | 51.8 | ||
| Calculate | ShearModulus | G(GPa) | 35.7 | 13.16 | 15.04 | 15.04 | 19.49 | |
| BulkModulus | B(GPa) | 93.1 | 34.3 | 39.2 | 39.2 | 50.08 | ||
Table 1: Characteristics and comparative elastic moduli of porous Ti5Mn alloys between porosity at (0%) and others.
To describe the dependence of porosities of Ti5Mn alloys on their theoretical relations have been proposed. The porosity range of the present study, there are various elastic modulus were obtained. Characterized each on varies porosities ranges (0%, 21%, 40%, 53% and 56%) have gotten elastic moduli of porous Ti5Mn alloys are 35.7 ≤ shear modulus G (GPa) ≥ 19.49 and 93.1 ≤ Bulk modulus B (GPa) ≥ 50.08 were observed to increase porosity P (%) given decreasing in modulus (E, G and B).
In Figure 1 it was cleared that the different of in modulus (E, G and B). Values Young’s modulus ≥ Bulk modulus ≥ shear modulus. Second hand noted that different Influence of porosity on Modulus of porous Ti5Mn alloys between 0% and others is biggest.
Reflection coefficients of Ti5Mn alloys porosity dependent
Characterized by (Longitudinal-Transverse-Rayleigh) angles: The scanning Acoustic microscopy (SAM) technique can to describe the reflection coefficient of Ti5Mn alloys as numerical calculation order to the displacement of all these critical angles is towards lower values when the porosity growths. We calculate R (?) phase from equation (1) for waves incident on the Ti5Mn alloys. The results obtained for the amplitude are illustrated in Figure 2, for porosity (0%) and other different porosity (21%, 40%, 53% and 56%). Some single R (?) phase of porous Ti5Mn alloys ranging (0%) and (21%, 40%, 53% and 56%).
Figure 2: Experimental phase of the reflection coefficient by way of roles the porous Ti5Mn alloys as (Longitudinal-Transverse-Rayleigh) angles.
Porosity were examined. The calculated Acoustic parameters VL, VT and VR, of these Ti5Mn alloys are reformed in Table 2, The effect of increasing porous Ti5Mn alloys on R (θ) is clarified improve in Figure 2 in terms of phase curves as a function of incident angles, θi. It would be made illustration that the phase change corresponds to the shear critical angle θS, (as indicated by the arrow in Figure 2). The slight shift between θS and θR is due to change of the Rayleigh velocity and shear velocity because to the fact that alternate in the porous Ti5Mn alloys. However, we can be observed, the reflection coefficient becomes unity, |R|=1, that means that all of the incident energy is reflected.
| Types | Ti5Mn alloys by diverse porosity (%) | |||||
|---|---|---|---|---|---|---|
| 0 (%) | 21 (%) | 40 (%) | 53 (%) | 56 (%) | ||
| Densityρ (Kgm-3) | 4500 | 4730 | ||||
| Poisson′s ratioσ | 0.32 | 0.33 | ||||
| Reflection coefficient R(?) | 89.6 | 178.7 | 155 | 150 | 118.6 | |
| longitudinal | ?L (dag.) | 9.34 | 13.87 | 12.22 | 12.22 | 10.72 |
| V(ms-1)L | 4617 | 3311 | 3539 | 3539 | 4029 | |
| transvers | ?T (dag.) | 18.77 | 26.62 | 24.79 | 24.79 | 24.63 |
| VT (ms-1) | 2326 | 1668 | 1783 | 1783 | 2030 | |
| Rayleigh | ?R (dag.) | 38.77 | 46.62 | 44.79 | 44.79 | 41.63 |
| VR (ms-1) | 2170 | 1559 | 1663 | 1663 | 1895 | |
Table 2: Experimental statistics of the reflection coefficient and calculation of longitudinal, transvers and Rayleigh velocities to porosity Ti5Mn alloys.
The critical angles θL=9.34°; 13.08°; 12.22°; 10.72°, θT=8.77°; 26.62°; 24.79°; 24.63°) and θR=38.77°; 46.62°; 44.79°; 41.63° at which arise these oscillations change due to effect porosity of Ti5Mn alloys (0%, 21%, 40% and 56%) increase on the critical angles respectively.
Quantization of Acoustic impedance for different porous Ti5Mn alloys
The following applet can be used to calculate the Acoustic impedance for any material, so long as its density (p) and Acoustic velocity (V) are known. The applet also shows how a change in the different porous Ti5Mn alloys effects on Acoustic impedance that is reflected and transmitted, Note that the fractional amount of transmitted sound energy plus the fractional amount of reflected sound energy equals one. The calculation used to arrive at these values will be conferred according to Eq. (2), (5) and (6). These results showed on Table 3. The characteristic Acoustic impedance is purely a property of the medium through which the wave is travelling. The units are Rayls=kgm-2s-1.
| Porous Ti5Mn alloys (%) | 0 | 21 | 40 | 53 | 56 | |||
|---|---|---|---|---|---|---|---|---|
| Densityρ (Kgm-3) | 4500 | 4730 | ||||||
| Poisson′s ratioσ | 0.32 | 0.33 | ||||||
| Types of Acoustic impedances(Z) | Rayleigh Acoustic impedance ZR (Mrayl) | 20.68 | 14.70 | 15.82 | 15.82 | 18.23 | ||
| Longitudinal Acoustic impedance ZL (Mrayl) | 21.03 | 16.09 | 17.09 | 17.09 | 19.37 | |||
| Transverse Acoustic impedance ZT (Mrayl) | 11 | 8.74 | 9.21 | 9.21 | 10.26 | |||
Table 3: Characteristic constant values in the rapport Acoustic impedance where represent (ZL, ZT and ZSolid) through shift up porosity of Ti5Mn alloys.
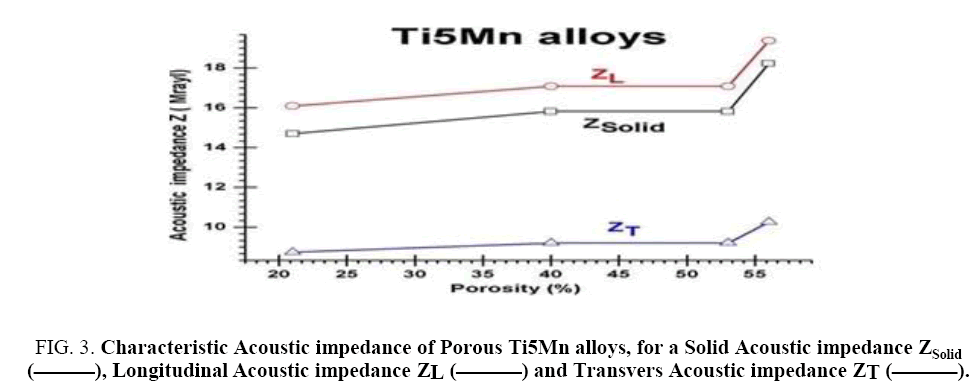
We also investigated several other Acoustic impedances (ZL, ZT and ZSolid) of Ti5Mn alloys. Contract us remembrance that the Acoustic impedance how variation, the obtained results are planned in Figure 3 that clarifies the effects of porous Ti5Mn alloys. On Acoustic impedance Figure 3: (Rayleigh or ZSolid, ( ), transverse, ZT, (ΔΔΔ) and longitudinal, ZL, (οοο)]. In general, Acoustic impedance of Ti5Mn alloys are very sensitive to studies variable porosities (0%, 21%, 40% and 56%), to measurement characterized Acoustic impedance (ZL, ZT, ZSolid).
), transverse, ZT, (ΔΔΔ) and longitudinal, ZL, (οοο)]. In general, Acoustic impedance of Ti5Mn alloys are very sensitive to studies variable porosities (0%, 21%, 40% and 56%), to measurement characterized Acoustic impedance (ZL, ZT, ZSolid).
Figure 3: Characteristic Acoustic impedance of Porous Ti5Mn alloys, for a Solid Acoustic impedance ZSolid ( ), Longitudinal Acoustic impedance ZL (
), Longitudinal Acoustic impedance ZL ( ) and Transvers Acoustic impedance ZT (
) and Transvers Acoustic impedance ZT ( ).
).
These marks set indication once more the behavior pragmatic in Figure 2 where the modifications in porous Ti5Mn alloys controlled to an increase in Acoustic impedances each points except at 0% in general, this initial increase is followed by a Quasi periodic and the porosity as 0% obey the rules as higher Impedance to Ti5Mn alloys than increasing to porous Ti5Mn alloys which porosity 0%, that ZL =21.03 , ZT =11 and ZSolid=20.68 all by Mrayl unity, while if porosities are (21%, 40% and 56%), ZL =(16.09, 17.09 and 19.37). Mrayl then ZT =(8.74, 9.21and10.26). Mrayl and ZSolid=(14.7, 15.82 and 18.23) Mrayl, respectively.
Conclusion
The severe phenomenon of Acoustic modes might appear or withdraw as result of Acoustic impedance. The importance of this investigation deceptions in the direct determination, for a assumed porous Ti5Mn alloys by recognized Young’s modulus experimentally, All the single R (?) phase of porous Ti5Mn were oriented using the scanning Acoustic microscopy (SAM) technique, it could to express the reflection coefficient and calculation of (Longitudinal-Transverse-Rayleigh) angles for porosity Ti5Mn alloys. The careful wanted Acoustic parameter (E, G, B, VL, VT, VR, θL, θT, θR, ZL, ZT and ZSolid) are Conclusive, with non-normal increasing or decreasing when must to increase to porous Ti5Mn alloys as (21%, 40% and 56%). In this work was allowed to viability application in Acoustic materials or used via data to researchers.
References
- LutjeringG, WilliamsJC. Titanium Springer-Verlag. Berlin.2003.
- Briggs A.AcousticMicroscopy, in Monographs on the Physics and Chemistry of Materials. Clarendon Press:Oxford.1992.
- Royer D.Elastic Waves in Solids. Springer-Verlag. Berlin Heidelberg. New York. 1996.
- Yu Z. Scanning Acoustic microscopy and its applications to materialcharacterization. RevMod Phys.1995;67:863-91.
- Geetha M, Singh AK, Asokamani R, et al. Ti based biomaterials, the ultimate choice for orthopedic implants-a review. Progr Mater Sci.2009;54:397-425.
- Zhang F, Weidmann A, Nebe BJ, et al. Preparation of Ti-Mn alloy by mechanical alloying and spark plasma sintering for biomedical applications. J Phys: Conf Ser.2009;144:012007.
- Garrett R, AbhayP, PanagiotisAD. Fabrication methods of porous metals for use in orthopedic applications. Biomat.2006;27:2651-70.
- Maev RG.Acoustic Microscopy Fundamentals and Applications.Wiley-VCH Verlag GmbH & Co.KGaA,Weinheim. 2008.
- Briggs GAD, RoweJM, Spencer DS.Quantitative Methods in Acoustic Microscopy. IEEE 1988 Symposium, 2008;pp:743-9.
- Maev RG, Levin VM. Basic principles of output signal formation in transmission raster Acoustic microscopy. Trans R Microsc Soc.1990;1:75-80.
- Weglein RD, Wilson RG. Characteristic materials signature by Acoustic microscopy. Electron Lett.1978;14:352-4.
- Levin VM, Maev RG,Kolosov OB, et al.Theoretical fundamentals of quantitative Acoustic microscopy. ActaPhysSlov. 1990;40:171-84.
- Zhang F, Lin K, Chang J, et al. Spark plasma sintering of macroporous calcium phosphate scaffolds from nanocrystalline powders. J Eur Ceram Soc.2008;28:539-45.
- Masayuki K, Hirakata LM, Asaoka K. Porous Ti-6Al-4V alloy fabricated by spark plasma sintering for biomimetic surface modification. J Biomed Mater Res.2003;68(1):88-93.
- Ibrahim A,ZhangF,OttersteinE, et al.Processing of porous Ti and Ti5Mn foams by spark plasma sintering. Mat and Design.2011;32:146-53.
- Briggs A. Advances in Acoustic Microscopy. Plenum Press. NewYork.1995.
- Doghmane M, Hadjoub F, Doghmane A,et al. Approaches for evaluating Young’s and Shear moduli in terms of a single SAW velocity via the SAM technique.Mater Lett.2007;61(3):813-6.
- Yu Z,Boseck S. Scanning Acoustic microscopy and its applications to material characterization. Rev Mod Phys.1995;67(4):863-91.
- Doghmane A,Hadjoub Z. Theoritical and experimental investigations of Acoustic materials signatures via variable-illumination lens-stop system.J PhysAppl Phys. 1997;30(20):2777-82.