Original Article
, Volume: 17( 1) DOI: 10.37532/0972-768X.2019.17(1).300New Compounds Derived from Stereoisomers of 2,4-Diphenylcyclobutane-1,3-Dicarboxylic Acids, 1,4-Diphenylcyclobutane-2,3-Dicarboxylic Acids and their Alkaloidal Precursors, The Truxillines: Theoretical Elucidation Based on PólyaâÂÂs Counting Theory
- *Correspondence:
- Emadak A , Theoretical Chemistry Unit of the Laboratory of Applied Physical and Analytical Chemistry, Faculty of sciences, University of Yaounde, Yaounde I, Cameroon, Tel: +237-694287365; E-mail: emadak@yahoo.com
Received: January 21, 2019; Accepted: February 11, 2019; Published: February 15, 2019
Citation: Emadak A, Patouossa I, Tchoutezo WS. New Compounds Derived from Stereoisomers of 2,4-Diphenylcyclobutane-1,3- Dicarboxylic Acids, 1,4-Diphenylcyclobutane-2,3-Dicarboxylic Acids and their Alkaloidal Precursors, The Truxillines: Theoretical Elucidation Based on Pólya?s Counting Theory. Int J Chem Sci. 2019;17(1):300
Abstract
New compounds derived from stereoisomers of 2,4-diphenylcyclobutane-1,3-dicarboxylic acids or truxillic acids, 1,4-diphenylcyclobutane-2,3-dicarboxylic acids or truxinic acids and their alkaloidal precursors, the truxillines, are elucidated through application of the Pólya’s formalism. The counting sequence of stereoisomers of those chemical compounds which belong to the family of heteropolysubstituted monocyclobutane derivatives is consistent with the chemical enumeration method using theorem of Pólya which comprises key steps such as representation of graph, permutation of symmetry’s operations, cycle index, topological and enantiomerical indicator and generating functions. This method leads to a system of equations which is solved to obtain the number of chiral and achiral graphs of stereoisomers of truxillic acids, truxinic acids and the truxillines among which few compounds are not yet chemically well-known.
Keywords
Pólya’s formalism; Truxillic acids; Truxinic acids; Chiral graphs; Achiral graphs
Introduction
2,4-diphenylcyclobutane-1,3-dicarboxylic acids or truxillic acids, 1,4-diphenylcyclobutane-2,3-dicarboxylic acids or truxinic acids and their alkaloidal precursors, the truxillines, have been extensively studied in chemistry [1-10]. Truxillic and truxinic acid derivatives are most known [5,6]. These two categories of diacids exist in a natural state in the sheets of coke and are also obtained by topochemical photodimerisation of the forms α and β of cinnamic acid [7]. In facts, Schmidt has established that the three different packing modes of cinnamic acid in the solid-state yield two different dimers upon irradiation: the α and β forms yield the anti-head-tail and the syn-head-head dimmers, respectively, and the γ-form is photoinert [8,9]. Chemistry of these acids was studied in 1919-1922 by German chemists Stoermer and Stobbe and coworkers [10-13]. Truxillic and truxinic acids can be used in the synthesis of analgesics [14] Alkaloidal precursors of those diacids, called truxillines, are a group of tropane alkaloids that have been of interest for over 100 years; the two most abundant isomers, alpha- and beta-truxilline, were structurally elucidated at the end of the nineteenth century [15-17]. They are found in some species of the families Solanaceae, Erythroxylaceae, Proteaceae, Euphorbiaceae, Rhizophoraceae, Convolvulaceae, and Cruciferae [18]. Furthermore, truxillines were detected and characterized in illicit cocaine and coca leaf by Moore et al. [19] The relative amount of truxillines in cocaine is indicative of the variety of coca used for cocaine processing, and thus, is useful in source determination [20]. The presence of truxillines in coca leaf is due to 2 + 2 photodimerization of cis-and/or trans-cinnamoylcocaine [21]. Considering the fact that literature is not widely extensive on the elucidation of stereoisomers of 2,4-diphenylcyclobutane-1,3-dicarboxylic acids, 1,4-diphenylcyclobutane-2,3-dicarboxylic acids and truxillines in regard with the quantity of papers published on those molecules, the focus of this study is to determine and design the structures of the exact number of all the chemical species belonging to this family of compounds through the use of Pólya’s theorem independently of the constraints of bonds strengths, thermodynamics properties and molecular stabilities.
Research Methodology
During the last decades, group theory has become an essential tool for chemists [22-24]. One of its applications to chemistry is to carry out a rigorous inventory of the chiral and achiral forms of a given chemical compounds [25,26]. The techniques of enumeration of the molecules made remarkable great strides thanks to progress of data processing and now make it possible to approach in a quantitative way all the fields of chemistry. Moreover, the inventory and the characterization of stereoisomers of a given family are essential in the modeling of this one and lead to discovered new chemical compound [27]. One of the most used methods is the Pólya‘s formalism [28,29] rising from its theorem which utilizes the indicating polynomial of cycles of the action of permutation G on the whole of the points of the parent graph and listed in Equation. 1 hereafter.
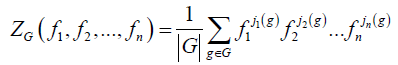 (1)
(1)
Where n is the order of group G and for each i going of 1 to n, ji(g) is the number of i-cycles of permutation associated to an element g belonging to G. Thus, the statement of this theorem becomes:
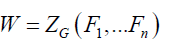 (2)
(2)
Where for each i going of 1 to n, Fi indicates the formal series given in Equation. 3:
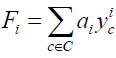 (3)
(3)
When we have a finite set of substituent C the formal series W and Fi are simply polynomials. Where yci is monomial function and ai the number of stereo-isomer having i substituent c ∈ C .
The various permutations of the eight sites of substitution of the monocycloalcane can be gathered in sets Z top and Z en respectively indicating the topological cycle indicator and the enamtiomeric cycle indicator. Indeed, the topological cycles indicator is obtained by adding all the cycle index generated by all the operations with parent group while the enantiomeric cycle indicator results from the summation of the cycle index resulting from the only proper rotation.
Mathematical formulation
Considering the fact that 2,4-diphenylcyclobutane-1,3-dicarboxylic acids, 1,4-diphenylcyclobutane-2,3-dicarboxylic acids and truxillines are organic compounds containing four-membered ring. Let us now consider the parent monocyclobutane as a three-dimensional object represented by the stereograph having a D4h global symmetry as shown in FIG. 1 [30-38].
The sixteen symmetry operations of this parent group are listed in Equation 4 hereafter:
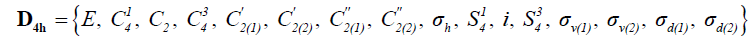 (4)
(4)
The eight sites of substitution of the stereograph of cyclobutane above form the unit (1, 2, 3, 4,1', 2', 3', 4'). While making act these various operations on unit sites of substitution, one obtains the table of the permutations recapitulated in Table 1 according to the direct notation, the notation by partition and index of cycle.
| Symmetry operations | Direct notation | Partition’s Notation | Cycle index |
|---|---|---|---|
| E | (1)(2)(3)(4) (1’) (2‘) (3‘) (4’) | [18] | f18 |
| C4 | (1, 2, 3,4) (1’,2’,3’,4’) | [42] | f42 |
| C2 | (1,3) (2,4) (1’,3’) (2’,4’) | [24] | f24 |
| C34 | (1, 4, 3,2) (1’,4’,3’2’) | [42] | f42 |
| C'2 (1) | (1,2’) (1’,2 ‘) (4,3’) (4’,3’) | [24] | f24 |
| C'2 (2) | (1,4) (1’,4’) (2,3) (2,3) | [24] | f24 |
| C''2 (1) | (1,1 ‘) (3,3’) (2,4’) (2’,4) | [24] | f24 |
| C''2 (2) | (2,2’) (1,3’) (4,4’) (1’,3) | [24] | f24 |
| σ h | (1,1’) (2,2’) (3,3’) (4,4’) | [24] | f24 |
| S4 | (1,2’, 3,4’) (1’, 2,3’,4) | [42] | f42 |
| i | (1,3’) (1’,3) (4,2’) (4’,2) | [24] | f24 |
| S34 | (1,4’, 3,2’) (1’, 4,3’,2) | [42] | f42 |
| σv (1) | (2,4) (2’,4’) (1) (1’) (3) (3’) | [22]. [14] | f22. f14 |
| σv (2) | (1,3) (1’,3’) (2) (2’) (4) (4’) | [22]. [14] | f22. f14 |
| σd (1) | (1,2) (1’,2’) (4,3) (4’,3’) | [24] | f24 |
| σd (2) | (1,4) (1’,4’) (2,3) (2’,3’) | [24] | f24 |
Table 1: Mixing proportions of cement slurry.
We derive the topological cycle indicator ( Z top ) and the enantiomeric cycle indicator ( Z en) from the above table in equation 5 and 6 respectively.
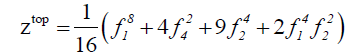 (5)
(5)
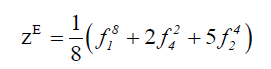 (6)
(6)
The cycle index used in Equation. 5 and Equation. 6 can be transform using Equation. 7 in the case of binary heterosubstition and which allows us to obtain the generating function given in Equation. 8.
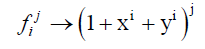 (7)
(7)
Where x and y represent the molecular weight of the substituent X and Y respectively. 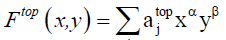 (8)
(8)
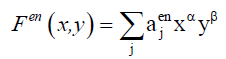 (9)
(9)
For each hetero-substitution with degree α and β , ajtop and ajen represent respectively the number of topolical isomers and the number of enantiomeric isomers. From these latters we can derive the number of chiral form and the number of achiral forms denoted by Ac and Aac using Equation. 10
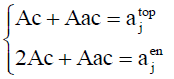 (10)
(10)
Results and Discussion
Truxillines, truxinic and truxillic acids are represented by this topological formula C4 H4 X2 Y2 where X and Y represent respectively (i) the carboxylic and phenyl groups for truxinic and truxillic acids and (ii) the methyl ecgonine esther and phenyl groups for truxillines.
(I) Let’us represent the molecular weight of carboxylic and phenyl groups respectively by x and y for the case of truxinic and truxillic acids. By application of Equations 5-9 we obtain these resulting generating functions:
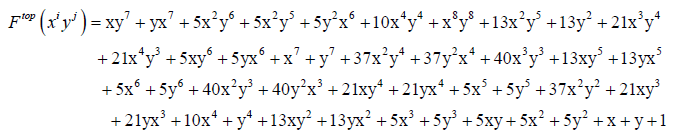 (11)
(11)
And
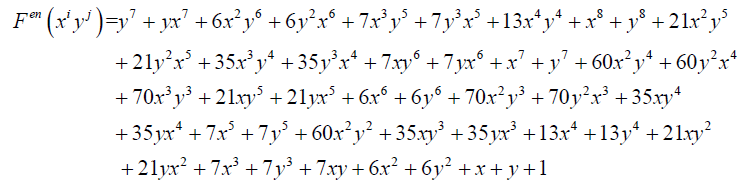 (12)
(12)
Now, let’s retain the corresponding term with our topological formula C4 H4 X2 Y2 . In other way we retain just the term corresponding to α =2 and β =2:
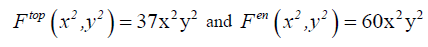 (13)
(13)
The number of chiral form and the number of achiral forms can be calculated using Equation 10.
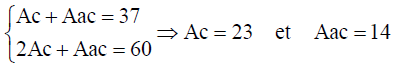 (14)
(14)
These calculations show that molecular system C4 H4 X2 Y2 exhibits a total number of 37 stereo and position isomers which are depicted by the molecular graphs shown in FIG. 2. The chirality fittingness reveals that this molecular system generates 23 chiral forms and 14 achiral forms.
Compounds of this molecular library of truxinic and truxillic acids can be subdivided into three (03) classes:
• Truxillic acids which are cyclobutane having two phenyls and two carboxylic groups symmetrically laid out compared to the diagonal of the cycle. There are five stereoisomers of the truxillic acid (trux1, trux2, trux3, trux4 and trux5 known in the literature as peri-, epi-, gamma-, alpha- and epsi-truxillic acid respectively [10-11]). These 5 compounds can be obtained by distillation of the cinnamic acid. They are also found in a large variety of plants [12-13].
• Truxinic acid stereoisomers in which the two carboxylic groups are carried by two adjacent carbons. It’s the case of following compound trux6, trux7, trux8, trux9, trux10 and trux11 [14].
• Unspecified truxillic/truxinic acids (from trux12 till trux37).
(II) Let’us represent the molecular weight of methyl ecgonine esther and phenyl groups respectively by x and y for the case of truxillines. By application of Eqs 5-9 we obviously obtain the same results for the molecular system C4 H4 X2 Y2 which exhibits a total number of 37 stereo and position isomers which are depicted by the molecular graphs shown in FIG. 2. The chirality fittingness reveals that this molecular system generates 23 chiral forms and 14 achiral forms which are also subdivided into two (02) classes:
• Truxillines which are cyclobutane having two phenyls and two methyl ecgonine esther groups symmetrically laid out compared to the diagonal of the cycle. There are five stereoisomers of the truxillines (trux1, trux2, trux3, trux4 and trux5 known in the literature as peri-, epi-, gamma-, alpha- and epsi-truxillines respectively).
• Truxillines stereoisomers in which the two methyl ecgonine esther groups are carried by two adjacent carbons. It’s the case of following compound trux6, trux7, trux8, truxil9, trux10 and trux11 [14].
• Unspecified truxillines (from trux12 till trux37).
Although certain molecules of this library are referred in the literature, it is to be hoped that others among the unspecified truxillic/truxinic acids and truxillines will be perhaps discovered in the nature or by way of synthesis. We are aware that severals will never exist taking into account their high degree of instability from the thermodynamic point of view.
Conclusion
This work was devoted to the elucidation of stereoisomers of truxillic/truxinic acids and truxillines in order to open the door to potential discovering of a new compound from the unspecified derivatives of 2,4-diphenylcyclobutane-1,3-dicarboxylic acids or truxillic acids, 1,4-diphenylcyclobutane-2,3-dicarboxylic acids or truxinic acids and their alkaloidal precursors, the truxillines. This has been done through the application of the method of Pólya to the enumeration of the stereoisomers of the truxillic/truxinic acids and truxillines which are a heterosubstituted cyclobutane of a quaternary nature of partial degree of substitution 2 for phenyl and 2 for the carboxylic acid or methyl ecgonine esther. Calculations shown that both compounds have 23 chiral forms and 14 forms achirals among its family members (diacids and non-diacids). The most known compounds of this series, because of their usefulness in chemistry are the truxillic acids, the truxinic acids and truxillines which are three categories of compounds obtained by natural way or synthesis. However unspecified truxillic/truxinic acids and truxillines are not forcing of less importance because it is undoubtedly from this third class of the truxillic/truxinic acids and truxillines that one could discover new molecules resulting from this family of compounds. The results obtained are in agreement with those that Emadak [31] obtained by associating graphs and permutation’s theory to enumerate the derivatives of the monocyclic cycloalcanes.
References
- Agarwai OP. Organic chemistry reactions and reagents. Krishna Prakashan Media. 2011.
- Liebermann A. Cinnamic acid polymers obtained from the minor alkaloids of cocaine. Berichte der Deutschen Chemischen Gesellschaft. 1888;21.
- Freedmana M, Mohadgera Y, Rennerta J, et al. β- and δ-truxinic acids. Organic Preparations and Procedures. 1969; 1(4):267.
- Kharkevich D, Fisenko V. On the comparative sensitivity of acetylcholine receptors to neuromuscular blocking agents. Archives internationales de pharmacodynamie et de thérapie. 1981;251:255-69.
- Krauze-Baranowska M. Truxillic and truxinic acids-occurrence in Plant Kingdom. Acta poliniae Pharmaceutica-Drug research. 2002;59(5):403-10.
- Hanley A, Russell W, Chesson A. Formation of substituted truxillic and truxinic acids in plant-cell walls-A rationale. Phytochemistry. 1993;33:957-60.
- Eliel E, Wilen S, Mander L. Stereochemistry of organic compounds. Wiley Interscience, New York. 1994;756.
- Natarajan A, Ramamurthy V. The chemistry of cyclobutanes, Wiley, New York, USA. 2005;807-72.
- Bassani D. The dimerization of cinnamic acid derivatives. CRC Handbook of Organic photochemistry and photobiology. 2004;2:1-20.
- Valery MD. Bioactive cyclobutane-containing alkaloids. J Nat Med. 2008;62:1-33.
- Stobbe H. Constitution of the truxillic acids and of truxone. Berichte Deutschen Chemischen Gesellschaft. 1919;52B:1021-8.
- Stoermer R, Laage E. Natural and artificial truxinic and truxinic acids. Berichte Deutschen Chemischen Gesellschaft. 1921;54B:77-85.
- Stobbe H, Steinberger F. Light reactions of the cis- and trans-cinnamic acids. Berichte Deutschen Chemischen Gesellschaft. 1922;55B:2225-45.
- Anastasiya S, Alla P, Nina K, et al. Synthesis and Analgesic Activity of New a-truxillic Acid Derivatives with Monoterpenoid Fragments. Med Chem Res. 2016;25:1608-15.
- Mallette J, Casale J. Rapid determination of the isomeric truxillines in illicit cocaine via capillary gas chromatography/flame ionization detection and their use and implication in the determination of cocaine origin and trafficking routes, Journal of Chromatography. 2014;1364:1-308.
- Hesse O. Zur kentnisse der cocablätter, Justus Liebigs Annalen der Chemistrie. 1892;27:180-228.
- Liebermann C. Ueber die Einwirkung der Schwefelsäure j-and D-isatropasäure, Berichte Deutschen Chemischen Gesellschaft. 1889;22:782-6.
- Griffin W, Lin G. Chemotaxonomy and geographical distribution of tropane alkaloids. Phytochemistry. 2000;53:623-37.
- Moore JM, Cooper DA, Lurie IS, et al. Capillary gas chromatographic-electron capture detection of coca-leaf-related impurities in illicit cocaine: 2,4-diphenylcyclobutane-1,3-dicarboxylic acids, 1,4-diphenylcyclobutane-2,3-dicarboxylic acids and their alkaloidal precursors, the truxillines. J Chromatography A. 1987;410:297-318.
- James M, John F, Donald A. Cooper, Comparative determination of total isomeric truxillines in illicit, refined, South American cocaine hydrochloride using capillary gas chromatography-electron capture detection. J Chromatography A. 1996;756:193-201.
- Lydon J, Casale J, Kong H, et al. The effects of ambient solar uv radiation of alkaloid production by erythroxylum novogranatense var. novogranatense. Photochem. Phytobiol. 2009;85:1156-61.
- Cotton FA. Chemical applications of group theory. Wiley-Interscience, New York. 1971.
- George D. Group Theory for chemist, Macmillan Physical Science Series. 1991.
- Alan V. Molecular symmetry and group theory: Q programmed introduction to chemical application. Wiley-Interscience, New York. 1971.
- Pólya G, Read RC. Combinatorial enumeration of groups, graphs and chemical compounds. Springer-Verlag, New York. 1987.
- Fujita S. Symmetry and combinatorial enumeration in chemistry. Springer-Verlag, New York. 1991.
- Milicevic A, Trinajstic N. Combinatorial enumeration in chemistry. Chemical modelling. 2006.
- Pólya G. Kombinatorische Anzahlbestimmungen für Gruppen, Graphen und chemische Verbindungen, Acta Mathematica. 1937;68(1).
- Harary F. Enumeration method of Redfield. Am J Math. 1967;89:2.
- Emadak A. Algorithme de dénombrement des graphes chiraux et achiraux d’un cycloalcane monocyclique hétérosubstitué. Académie des sciences. 2002;5:533-9.
- Emadak A. Application de la théorie des graphes au dénombrement des dérivés des cycloalcanes monocycliques, Thèse de Doctorat/Ph.D., Université de Yaoundé I. 2006.
- Wedad A, Baddar FG, Omara MA. Polycyclic aromatic compounds. The conversion of 1,1,4-triarylbuta-1,3-diene-2,3-dicarboxylic anhydrides and 1,4-diarylnaphthalene-2,3-dicarboxylic anhydrides into polycyclic compounds. J Chem Soc Org Chem. 1971.
- Elina AS, Musatova IS. Synthesis of derivatives of pyrazine-2,3-dicarboxylic acids and pyrazine-2,3-dicarbonamides from 2,3-dichloroquinoxaline. Chem Heterocycl Compd. 1973;9(11):1403-6.
- Miskolczi I, Zékány A, Rantal F, et al. Diastereo- and Regioisomeric Bicyclic Thiohydantions from Chiral 1,3-Thiazolidine-2,4-dicarboxylic acids. Helvetica. 1998;81(3):744-53.
- Morikawa A, Hatakeyama T. Synthesis and characterization of novel aromatic polyamides from 1,4-Bis(4-aminophenyl)-2,3-diphenylnaphthalene and aromatic dicarboxylic acids. Polymer J. 1999;31:66-9.
- Zieliński T, Kȩdziorek M, Jurczak J. Bisamides derived from azulene-1,3- and -5,7-dicarboxylic acids as new building blocks for anion receptors. Chem A Eur J. 2008;14(3):838-46.
- Dong WC, Hyo JL, Jong HK, et al. Quinoxaline-2-carboxylic acids and quinoxaline-2,3-dicarboxylic acids. Organic Letters. 2011;13(15):3880-3.
- Alizadeh A, Hosseinpour R, Rostamnia S. Synthesis of 4-hydroxy-1h-pyrrole-2,3-dicarboxylic acids. Synfacts. 2008;12:1271.


