Original Article
, Volume: 15( 2)Modelling the Absorption Process of Water in Wood in the Transient Regime
- *Correspondence:
- Tarik Ainane Laboratory of Analytical Chemistry and Physical Chemistry of Materials, Faculty of Sciences Ben Msik, University of Hassan II, BP 7955, Casablanca, Morocco
Tel: 00212634576500; E-mail: ainane@gmail.com
Received Date: May 09, 2017 Accepted Date: May 16, 2017 Published Date: May 18, 2017
Citation: Bennani L, Elkouali M, Talbi M, et al. Modelling the Absorption Process of Water in Wood in the Transient Regime. Int J Chem Sci 2017;15(2):137.
Abstract
The process of absorption of water by way of wood in 3-dimensions can be described mathematically by analytical solutions, whether initial conditions aren’t simples e.g., when there is a profile of concentration at the beginning of a stage of absorption, only numerical model scan be used. The transport of water is then obtained below the fiber saturation point. The potential which drives the transport of the bound-water and the free-water through the wood has been considered by testing a diffusional transport model. The transient diffusion with a constant diffusivity has been tested to describe the process. Analytical solutions have been successfully used to describe the stage of absorption. A model based on numerical method with finite differences has been found to describe the process and especially when the equilibrium of absorption has not been attained and diffusion coefficient parameter in the models was obtained by fitting the model predictions with the experimental data. Finally, water absorption of the studied wood was proved to follow the kinetics of a transient regime.
Keywords
Wood; Water absorption kinetics; Transient regime; Modeling
Introduction
The movement of moisture through is very complex process. Moisture in wood exists in three basic forms: bound water within the cell wall, free water in liquid form, as well as water vapor, in the voids of the wood. In general, water can move through wood in three forms: as water vapor through the cell cavities and permanent pores, as bound water in the wood substance and as free liquid water in the same structure [1-10].
When the surrounding atmosphere air, the moisture content is below the fiber saturation point, this fiber saturation point being attained when the relative humidity of air is 100%. When the surrounding medium is water, the moisture content is beyond the fiber saturation point [11,12].
Many studies have been made concerning the transport of moisture below the fiber saturation point. Very often, the transport of water is describing bed in terms of diffusion, the gradient of moisture content being considered as the driving force. In this case, the bound water and water vapor diffuse [13-18].
The problem of the water above the fiber saturation point is of high interest, because the presence of free water in wood drastic cally in creses its susceptibility as well as the development of fungal attacks [19,20]. However, few studies have been in this case. This problem being said to the somewhat more complicated because of the presence of free water in addition with the bound water and water vapor [21,22].
The main objective of this study is to describe the process of absorption of water, when the moisture is he beyond the fiber saturation point. The wood sample is then considered with tree directions of transport: radial, tangential and longitudinal. The second purpose of this works to build a mathematical model capable of describing the process of absorption of moisture below of saturation point, when the wood is contact with liquid water. In spite of the fact that the bound water could be transported in response to a vapor pressure gradient [23,24], we have assumed with the vast majority of wood scientists that the gradient of moisture content in the driving force for the water transport [25-29].
Materials and Methods
Theoretical basis
Assumptions: In order to clarify the problem both for the analytical treatments and numerical analysis, the following assumptions are made:
1) A tree dimensional transfer of moisture through the wood is considered.
2) These moisture transports are controlled by transient diffusion within the wood. The principal directions of diffusion are: the longitudinal, the radial and the tangential with the principal diffusivities DL, DR and DT.
3) The diffusivities are constant, as they are found from experiments.
During the step of absorption, the concentration of moisture on the wood surface reaches the equilibrium value as soon as the wood is immersed in water.
Mathematical treatment: In the axes Ox, Oy and Oz coincide with the three principal’s directions of diffusion (Figure. 1), the general equation of diffusion in tree-dimensions with constant diffusivities is:
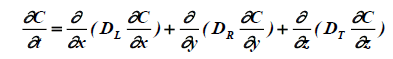 ( 1 )
( 1 )
Where DL, DR and DT are the principal diffusivities along the longitudinal, radial and tangential axes.
Initial and boundary conditions are:
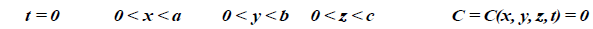 (2)
(2)
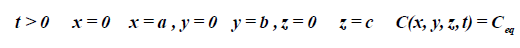 (3)
(3)
• a, b, c are the sides of the parallelepiped.
• C (x, t): Is the concentration of liquid in the plate at time t and abscissa x.
• Ceq: Is the concentration obtained at equilibrium.
The kinetics of the transport of three-way material is obtained by making the product of the analytical solutions obtained for each direction of the transfer:
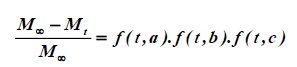 (4)
(4)
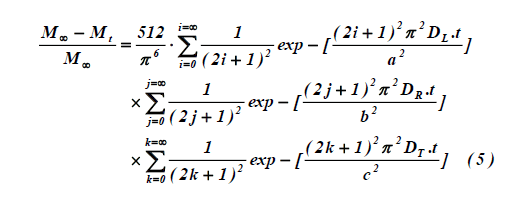
With a parallelepiped of sides are: a, b and c, and principal diffusivities are: DL, DR and DT.
In the case of absorption, the amount of moisture transferred can also be expressed by the equation:
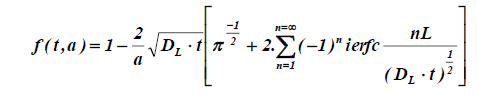 (6)
(6)
This equation being transformed for shorts times (Mt/M∞<0.5) into the simple well-known equation:
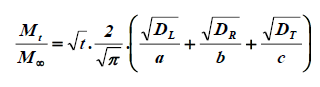 (7)
(7)
Numerical analysis
An explicit Numerical method with finite differences issued. Each dimension of the board is divided into equal finite slices of dimension ΔL, ΔT and ΔR and each position in wood is defined by three integers i, j, k such as:
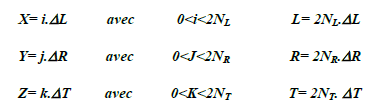 (8)
(8)
Time is divided into equal intervals Δt
Concentration within the wood
The water balance during the increment Δt is calculated within the small parallelepiped. of dimensions ΔL, ΔT and ΔR, by considering longitudinal, radial and tangential diffusion. The new concentration CNi, j, k at position i, j, k after step of time Δt is thus expressed in terms of previous concentrations C obtained at the same place and adjacent places for 1 ≤ I ≤ NL, 1 ≤ J ≤ NR and 1 ≤ K ≤ NT:
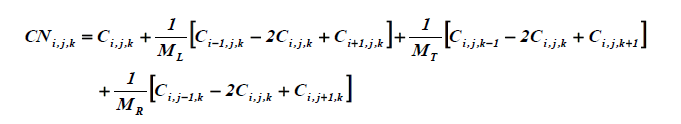 (9)
(9)
With the dimensionless numbers ML, MR and MT:
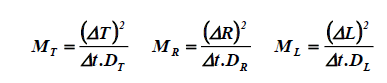 (10)
(10)
Concentration in surface:
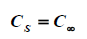 (11)
(11)
Amount of water located in the sample
The amount of moisture located in the sample is calculated by integration the concentration with re spect to space. Is used two auxiliary’s variables VA and VB:
For 1 ≤ I ≤ N and 1 ≤ j ≤ N:
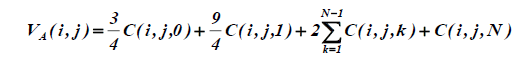
For 1 ≤ I ≤ N:
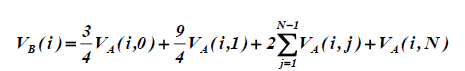
Finally:
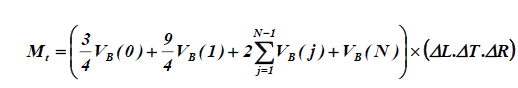 (12)
(12)
Conditions of stability for calculation
In the right member of equation 12, the total coefficient for C (0,0,0) must ti be positive. The increment of time Δt must be chosen so that:
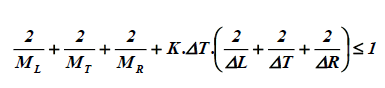 (13)
(13)
Experimental Procedure
Wood samples: Several samples of sapwood (pin maritine) are used in this study. They are cut in such way that their three axes are the same as the tree principal axes of diffusion. Various samples of wood are used either to the determination of principal diffusivities are displayed in Table 1.
| Sample 1 | (L=2 cm, R= 0.5 cm, T= 2 cm) |
| Sample 2 | (L=2 cm, R=1 cm, T= 2 cm) |
| Sample 3 | (L=2 cm, R=2 cm, T=0.8 cm) |
Table 1. The dimensions of the samples used.
Experiments: The samples previously equilibrated in air at a RH a little 40%, are immersed in water at defined temperature. The process of absorption is followed by weighing the samples at intervals, until the weight remains constant.
Results and Discussion
The values obtained in this study for diffusivity are given in Table 2. These values of parameters DL, DR and DT, as well as the assumption of transient diffusion have been tested by considering a constant diffusivity with the help of analytical solutions and with the help of the numerical model. As shown in Figure. 1 good agreement is obtained between experiments and the values obtained by calculations. The numerical model describes the process of absorption during the whole process.
| Principal axis | Symbols | Diffusivity *105 (cm2/s) |
|---|---|---|
| Longitudinal | DL | 8 |
| Radial | DR | 0.5 |
| Tangential | DT | 0.4 |
Table 2. Values of parameters of diffusivity.
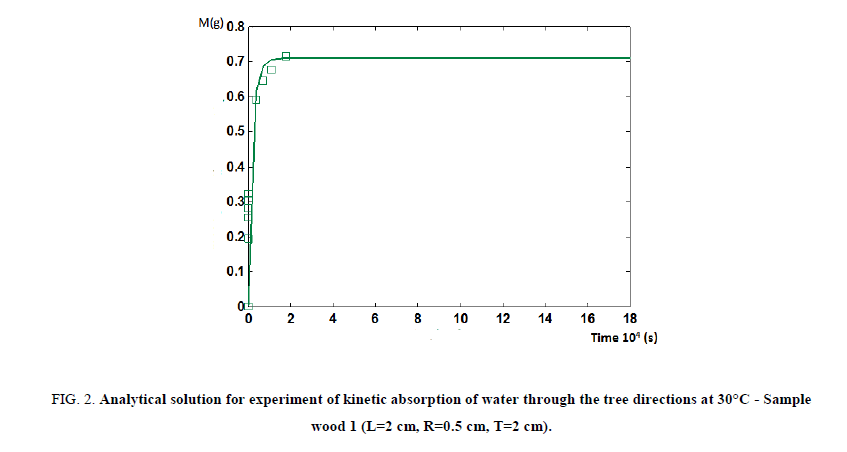
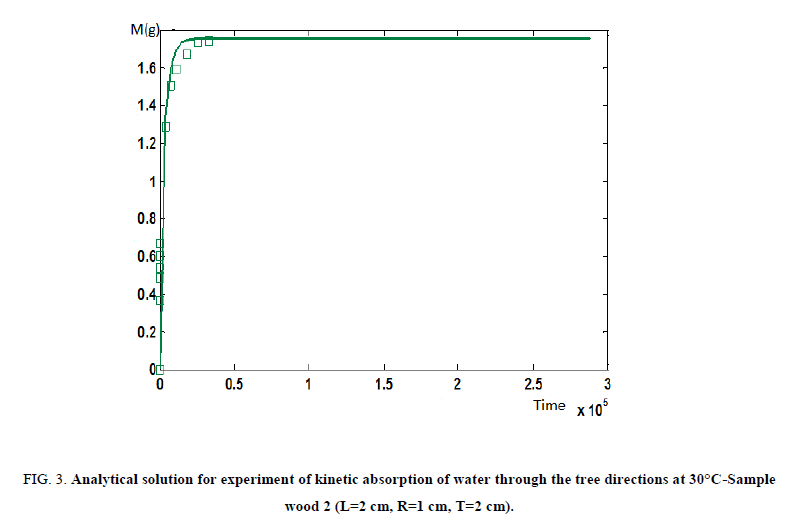
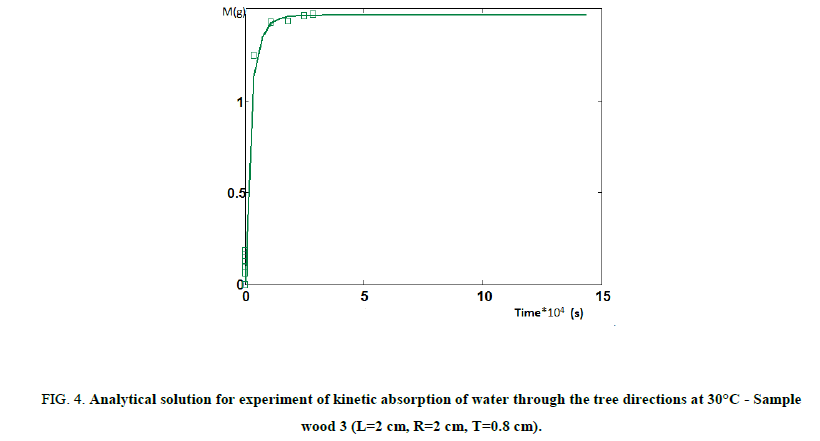
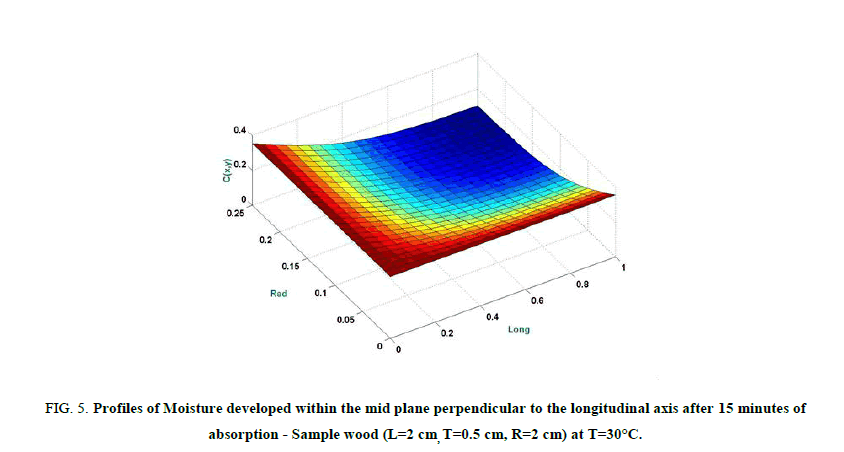
In the other hand, the profiles of moisture content an easily calculated with numerical model. In spite of the fact that is difficult to determine how valid they are by experiment, these experiments being tedious and destructive. These profiles can give a good idea of the contribution of each transport (longitudinal, radial, tangential) at any place and time. Consequently, Figures. 2-4 show the analytical solutions of the kinetics of water absorption in the different samples sizes (1, 2 and 3), also Figure. 5 gives the graphical representation of the sample of the wood by description of profiles of moisture developed within the mid plane perpendicular to the longitudinal axis after 15 minutes of absorption.
Figure 2: Analytical solution for experiment of kinetic absorption of water through the tree directions at 30°C - Sample wood 1 (L=2 cm, R=0.5 cm, T=2 cm).
Figure 3: Analytical solution for experiment of kinetic absorption of water through the tree directions at 30°C-Sample wood 2 (L=2 cm, R=1 cm, T=2 cm).
Figure 4: Analytical solution for experiment of kinetic absorption of water through the tree directions at 30°C - Sample wood 3 (L=2 cm, R=2 cm, T=0.8 cm).
Figure 5: Profiles of Moisture developed within the mid plane perpendicular to the longitudinal axis after 15 minutes of absorption - Sample wood (L=2 cm, T=0.5 cm, R=2 cm) at T=30°C.
Conclusion
The process of absorption of water is studied by considering the three-dimensional transfer with tree principal directions of diffusion. Numerical models with differences are able to describe the process of absorption under tree direction. The validity of these models is determined by comparing the theoretical kinetics of absorption with the experimental kinetic. The profiles of moisture content evaluated within the sample are able to gain a full model on the process.
References
- Hossienzadeh S, Ghorbani M, Beparva P. Effect of colloidal silica nanoparticles produced from rice husk on dimensional stability and water absorption of poplar wood (Populus deltoides). 2014;pp:763-73.
- Manickam JR. Study of water soluble dyes adsorption from aqueous solution by Prosopis spicigera L. wood (PSLW) carbon. Ind J Chem Tech. 2016;23:22-30.
- Mounji H, El Kouali M, Vergnaud JM. Process of absorption of moisture by wood in case of condensation. Modelling and experiment. J Pol Eng. 1993;12:197.
- Waldron L, Cooper PA. Prediction of long-term leaching potential of preservative-treated wood by diffusion modeling. Holzforschung. 2005;59:581-8.
- Bouzon J, Haloui A, Vergnaud JM. Study of the release in water of a chemical used for preservation of wood. Effect of the dimensions of the wood. Wood sci tech. 1996;30:443-54.
- Lebow ST. Evaluating the leaching of biocides from preservative-treated wood products. In Deterioration and Protection of Sustainable Biomaterials. Am Chem Soc. 2014;pp:239-54.
- Bahmani M. Residual metal content and metal distribution in chromium/copper-treated wood after field and laboratory leaching exposure. Eur J Wood & Wood Pro. 2015;73:377-84.
- Kouali M, Vergnaud JM. Modeling the process of absorption and desorption of water above and below the fiber saturation point. Wood Sci Tech. 1991;25:327-39.
- Kouali M, Bouzon J, Vergnaud JM. Process of absorption and desorption of water in a wood board, with 3-dimensional transport beyond the FSP. Wood sci tech. 1992;26:307-21.
- Vergnaud, Jean-Maurice. Drying of wood. Drying of polymeric and solid materials. Springer London. 1992;pp:229-75.
- Wharton GW, Kanungo K. Some effects of temperature and relative humidity on water-balance in females of the spiny rat mite, Echinolaelaps echidninus (Acarina: Laelaptidae). Annals Entomol Soc Am 1962;55:483-92.
- Wang HR. Measurement and numerical simulation of moisture transport within potash beds as a prelude to moisture migration caking. Adv Pow Tech. 2006;17:29-47.
- Le CV, Ly NG, Postle R. Heat and mass transfer in the condensing flow of steam through an absorbing fibrous medium. Int J Heat Mass Trans. 1995;38:81-9.
- Yeboah SK, Darkwa J. A critical review of thermal enhancement of packed beds for water vapour adsorption. Ren Sust Ener Rev. 2016;58:1500-20.
- Tatyana L. Acid-modified clinoptilolite as a support for palladium–copper complexes catalyzing carbon monoxide oxidation with air oxygen. Chem Cent J. 2017;11:28.
- Brojeswari D. e-Moisture transmission through textiles. Part I: processes involved in moisture transmission and the factors at play. AUTEX Res J. 2007;pp:2s.
- Halder A, Ashish D, Ashim KD. Modeling transport in porous media with phase change: applications to food processing. J Heat Trans 2011;133:031010.
- Rabia YA, Haloui A, Vergnaud JM. A method for reducing the amount of PCP in wood with less detriment to protection against fungi. Mod Sim Mat Sci Eng. 1996;4:1.
- Müller U. Detection of fungal wood decay using magnetic resonance imaging. Eur J Wood and Wood Pro. 2001;59:190-4.
- Cooke R, Kuntz ID. The properties of water in biological systems. Ann rev biophy bioeng 1974;3:95-126.
- Kramer PJ, Boyer JS. Water relations of plants and soils. Academic press. 1995.
- Hinckley TM, James PL, Steven WR. Temporal and spatial variations in the water status of forest trees. For Sci. 1978;24:a0001-z0001.
- Dickinson RE. Modeling evapotranspiration for three?dimensional global climate models. Cli pro cli sen. 1984;pp:58-72.
- Cloutier A, Yves F. A model of moisture movement in wood based on water potential and the determination of the effective water conductivity. Wood Sci Tech. 1993;27:95-114.
- Cloutier A, Carl T, Yves F. Effect of specimen structural orientation on the moisture content—water potential relationship of wood. Wood Sci Tech. 1995;29:235-42.
- Defo M, Cloutier A, Fortin Y. Modeling vacuum-contact drying of wood: The water potential approach. Dry Tech 2000;18:1737-78.
- Shi SQ. Diffusion model based on Fick’s second law for the moisture absorption process in wood fiber-based composites: Is it suiTable or not? Wood Sci Tech. 2007;41:645-58.
- Zhang Z, Dong-yan, Li-ping S., et al. Modeling of temperature-humidity for wood drying based on time-delay neural network. J For Res. 2006;17:141-4.
- Kang W, Woo YC. Liquid water diffusivity of wood from the capillary pressure-moisture relation. J wood sci 2009;55:91-9.