Original Article
, Volume: 13( 1)Investigation of One-Dimensional Spin Glass Using Combinatorial Factor Method
- *Correspondence:
- Darioush Sharafie, Department of Chemistry, Science College, Razi University, Kermanshah, Iran, Tel: 989123214247; E-mail: sharafie@cfu.ac.ir
Received: December 18, 2017; Accepted: January 18, 2018; Published: January 22, 2018
Citation: Sharafie D, Ranjbar S. Investigation of One-Dimensional Spin Glass Using Combinatorial Factor Method. Phys Chem Ind J. 2018;13(1):118
Abstract
Ising model as a simplified model of reality, exhibits phase transition. Combinational factor method is a numerical method which is applied for infinite lattices with a limited number of rows or small m. In this work, we used the combinatorial factor method to find the thermodynamic properties of the spin glass (A1-xBx). For simplicity, we supposed that, the spin glass can be considered as one-dimensional lattice with nearest neighbor interactions. For this model, having an exact combinatorial factor and accordingly the corresponding exact energy, the Helmholtz free energy is minimized. Overall, one dimensional spin glass does not show phase transition as like as one-dimensional Ising model. There are same trends in temperature and entropy in this model, in both constant x and f cases, a same trend was seen for maximum of heat capacity (where f is constant, and Coefficient is interaction energies between the nearest neighbor pair of ii.).
Keywords
Ising model; Combinatorial factor; Spin glass; Phase transition
Introduction
Ising [1-4] model includes discrete variables displaying magnetic moment of atomic spins which could be one of two possible states namely +1 or -1 [5,6]. This model as a simplified model of reality, exhibits phase transition [7,8]. Spin glasses [9] are disordered system in which the disorder is such strong that there is a competition between different terms in the Hamiltonian which is called frustration [10]. In spin glass, which also have disorder, it turns out that there are some states in which the orientation of a large number of spin are different from ground states, but they are close in energy with that. There are barriers on all scales and so a spin glass at low temperatures will have very slow dynamics and never fully equilibrate [11]. So, the spin glass does indeed constitute a new state of magnetism, distinctly different from the long-rang ordered Ferro and antiferromagnetic phases [12]. In addition, a spin glass exhibits high magnetic frustration. The origin of the behavior can be either a disordered structure (such as that of a conventional, chemical glass) or a disordered magnetic doping in an otherwise regular structure. Since spin glasses have a lot of ground states, exploring those have not been achieved in experimental time scales. Unusual experimental properties make spin glasses an appealing area of extensive theoretical and computational investigations. Based on a set of replicas of partition function of the system, mean field theory is vastly used in a great deal of early theoretical studies on spin glasses. Sherrington and Kirkpatrick had introduced an influential exactly solvable model of spin glasses [5]. Modelling of slow dynamics of magnetization and complex non-ergodic equilibrium state was introduced as theoretical extensions of their work.
Spin glass systems have been extensively investigated in condensed matter physics. In the simplest scheme, Spin glass are considered as a collection of classical spins with quenched random frustrated interactions. A frozen disordered state is the lowest-temperature state. This state has zero magnetization while the local spontaneous magnetization at a given site is nonzero. Quantum systems may also show glassy behavior [13].
Methods
We consider a one-dimensional spin glass, which is conformed of two interacting particles as A and B so that, the numbers of these equal NA and NB , respectively 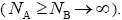 The chemical formula for such lattice may be considered as
The chemical formula for such lattice may be considered as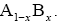 For simplicity, in this lattice nearest neighbors merely have been considered. Nearest neighbor’s energy is considered as
For simplicity, in this lattice nearest neighbors merely have been considered. Nearest neighbor’s energy is considered as 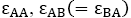 and
and 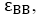 where
where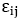 s are the interaction energies between the nearest neighbor pair of ij. With the assumption of
s are the interaction energies between the nearest neighbor pair of ij. With the assumption of 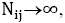 where
where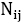 is the number of pairs of ij, we could write the total energy of the lattice as:
is the number of pairs of ij, we could write the total energy of the lattice as:
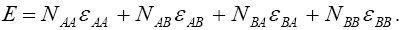 (1)
(1)
Considering a regular configuration for this lattice as:
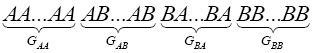 (2)
(2)
And relating the values of 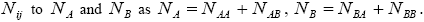
Assuming that, the interaction energies between pairs are as follow 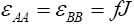 and
and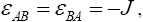 where J and f is a constant ( f > 0) . The total energy can be written as:
where J and f is a constant ( f > 0) . The total energy can be written as:
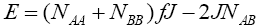 (3)
(3)
In this work, authors are interested in knowing that how many different configurations with this energy, E, exist? In other words, how many different configurations, 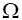 with the same value of
with the same value of 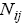 s are available? To answer this question, first we consider all distributions in which A is involved. Thus, irrespective of
s are available? To answer this question, first we consider all distributions in which A is involved. Thus, irrespective of 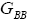 group first, we may calculate the total number of possible ways for distribution of
group first, we may calculate the total number of possible ways for distribution of 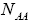 indistinguishable pairs on
indistinguishable pairs on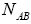 pairs, in such a way that the number of each of them remains constant. The number of this distribution,
pairs, in such a way that the number of each of them remains constant. The number of this distribution, 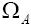 is,
is,
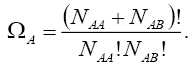 (4)
(4)
Then, similar to step 1, we may find the number of distributions in which B is involved, as 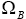 :
:
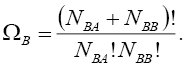 (5)
(5)
Due to the fact that these distributions are independent of each other, the total number of configurations, 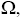 for such lattice with the nearest neighbor interaction energy, can be given as:
for such lattice with the nearest neighbor interaction energy, can be given as:
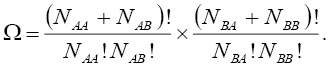 (6)
(6)
With regard to chemical formula 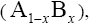 we can write
we can write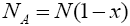 and
and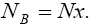
Where N is 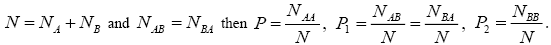
From solving nonlinear equations, we can derive thermodynamic properties of lattice. Using the Stirling’s approximation, the reduced Helmholtz free energy, reduced heat capacity and reduced entropy are:
 (7)
(7)
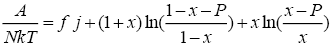 (8)
(8)
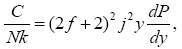 (9)
(9)
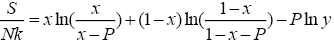 (10)
(10)
Where 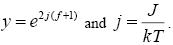
Results and Discussion
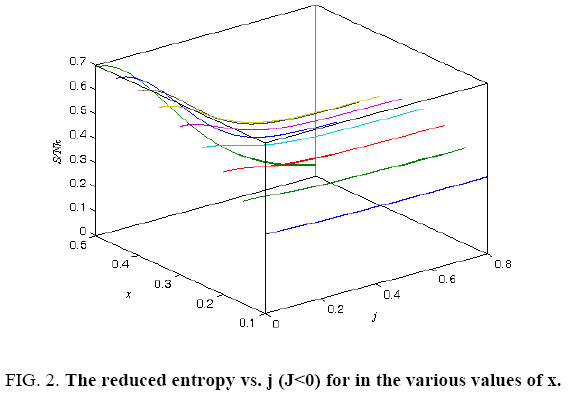
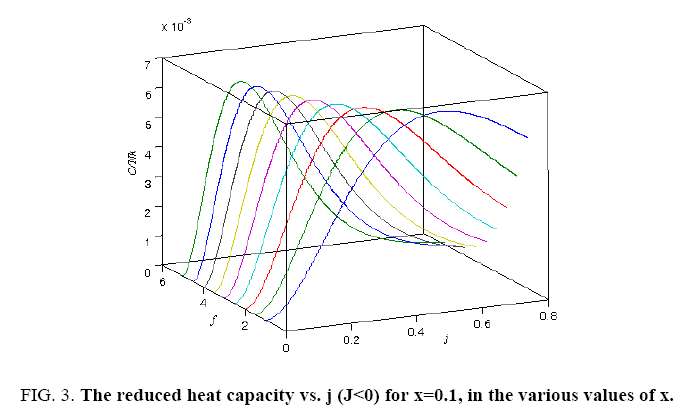
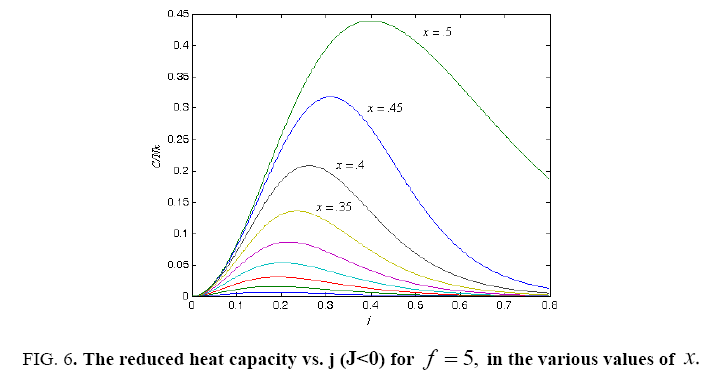
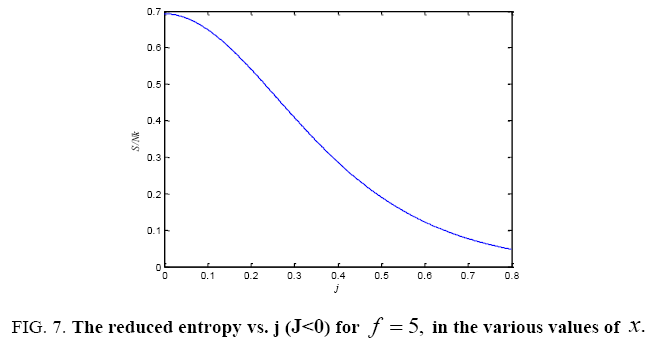
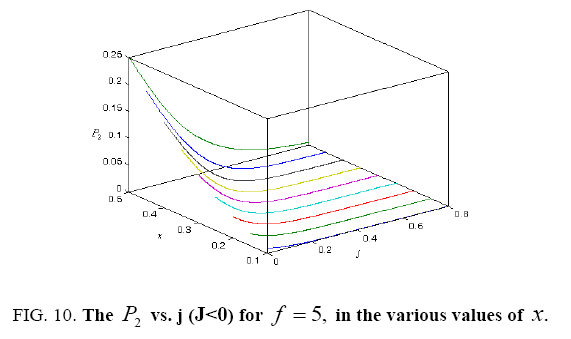
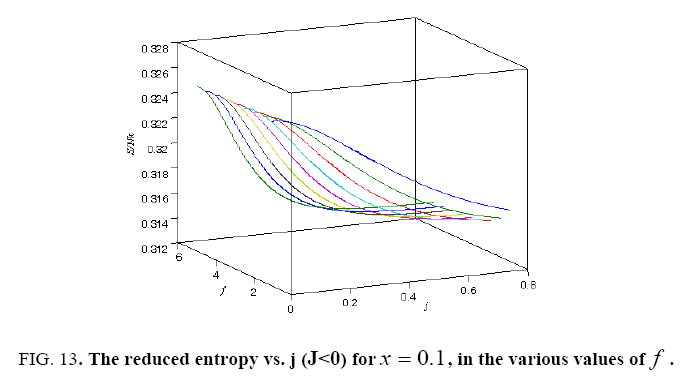
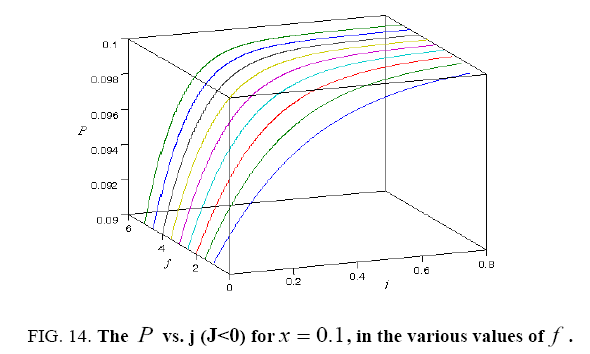
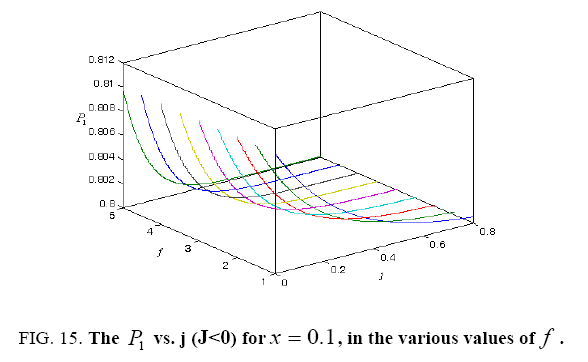
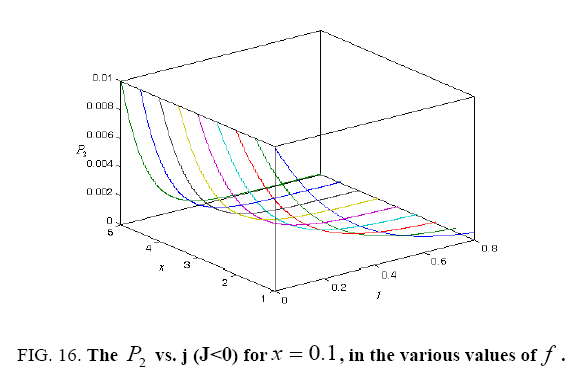
All calculations were carried out by a personal computer, using well-known software called Matlab. According Figure 1, we see that, in constant f when x rises, the maximum of each heat capacity increases. So that, for x = 0.5 (Ising model) the critical point of this heat capacity riches to its maximum value. In Figure 2, one could see that, when the temperature decreases, the entropy decreases, too. Also, in each temperature, when x rises, the entropy also increases. We see that, in constant x when f rises the maximum of each heat capacity increases (Figure 3). The results of these calculations for the reduced Helmholtz free energy, internal energy, entropy, and the reduced heat capacity are given in supplementary files [14-16] (Figure 4-16).
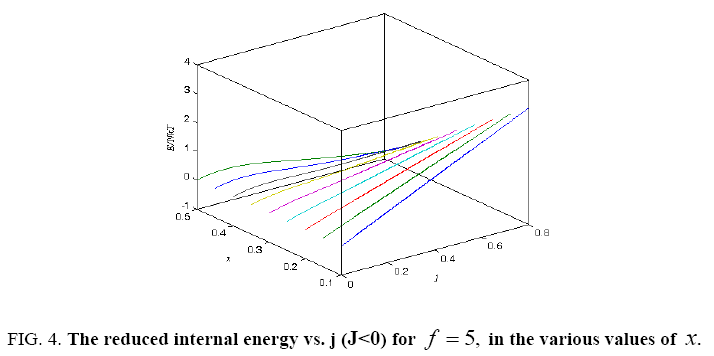
Figure 4: The reduced internal energy vs. j (J<0) for f = 5, in the various values of x.
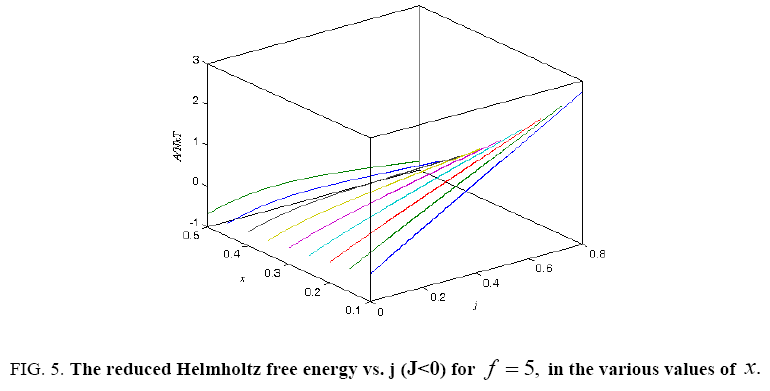
Figure 5: The reduced Helmholtz free energy vs. j (J<0) for f = 5, in the various values of x.
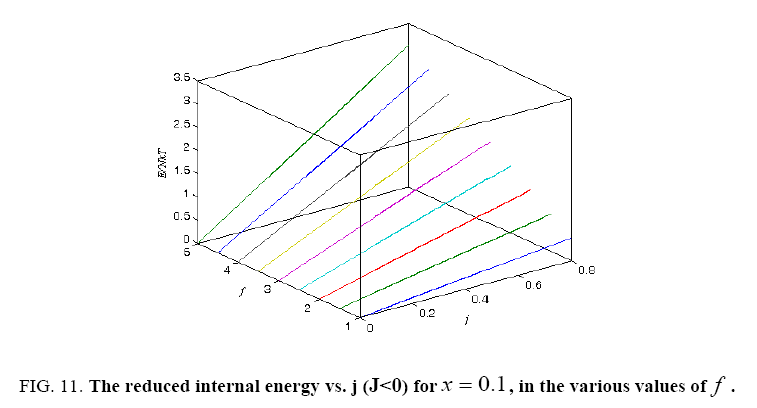
Figure 11: The reduced internal energy vs. j (J<0) for x = 0.1, in the various values of f .
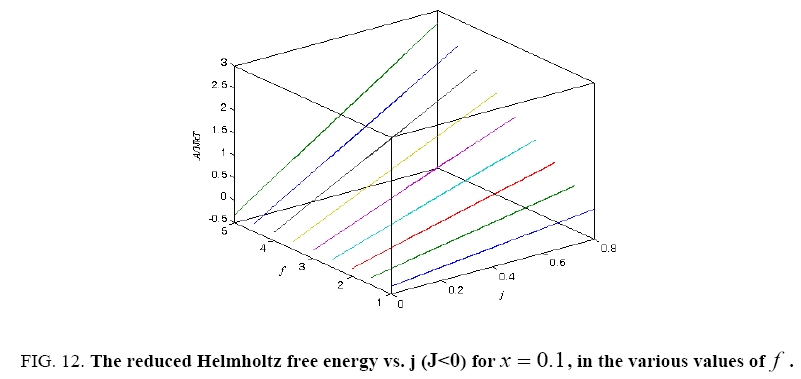
Figure 12: The reduced Helmholtz free energy vs. j (J<0) for x = 0.1, in the various values of f .
Conclusion
Using combinatorial factor method, thermodynamic properties of the spin glass have been found. Spin glass have been considered as a one-dimensional lattice which merely interact with its nearest neighbor. Analyzing figures, we conclude that all of the thermodynamic properties are depended on j and the two parameters x and f . What is more important is that as like as one-dimensional Ising model, in the one-dimensional spin glasses, we cannot see any phase transition.
Acknowledgements
We would like to thank Razi University for financial support.
References
- Lucas A. Isingformulations of many NP problems. Front Phys. 2014;2:5.
- Suzuki S, Inoue J, Chakrabarti BK. Quantum ising phases and transitions in transverse Ising models. Introduction to Polarization Physics. 2013;859:1.
- Bhatt RN, Young AP. Search for a transition in the three-dimensional J ising spin-glass. Phys Rev Lett. 1985;54(9):24.
- Vicente A, Di Carlo G, Follana E, et al. Antiferromagnetic Ising model in an imaginary magnetic field. Phys Rev E. 2017;96(3):032114.
- Sherrington D, Kirkpatrick S. Solvable model of a spin-glass. Phys Rev Lett. 1975;35:1792.
- Venturelli D, Mandrà S, Knysh S, et al. Quantum optimization of fully connected spin glasses. Phys Rev X. 2015;5(3):031040.
- Dillenschneider R. Quantum discord and quantum phase transition in spin chains. Phys Rev B. 2008;78(22):224413.
- Xue D, Zhou Y, Ding X, et al. the transitions from glassy state to long-range-ordered state in ferroic glasses. Physica Status Solidi (B). 2014;251(10):2019-26.
- Lidar DA, Biham O. Simulating Ising spin glasses on a quantum computer. Phys Rev E. 1997;56(3):3661-81.
- Ilker E, Berker AN. Overfrustrated and underfrustrated spin glasses in d=3 and 2: Evolution of phase diagrams and chaos including spin-glass order in d=2. Phys Rev E. 2014;89(4):042139.
- Young AP. Numerical studies of spin glass problems in magnetism and superconductivity. Physica B Condens Matter. 2002;321(1-4):183-8.
- Mydosh JA. Spin glasses:An experimental introduction. London; Taylor and Francis. 1993. 256.
- John S, Quang T. Quantum optical spin-glass of impurity two-level atoms in a photonic band gap. Phys Rev. 1996;76(8):1320.
- Ranjbar S. The combinatorial factor method for solving Ising model. Chemical Physics. 2006;326(2-3):483-8.
- Ranjbar S, Hossini SJ. The combinatorial factor method for investigation of order-disorder in two-dimensional binary alloy. J Iran Chem Soc. 2010;7(4):986-94.
- Ranjbar S. The combinatorial factor method for investigation of surface adsorption. J Iran Chem Soc. 2010;7(1):84-94.