Original Article
, Volume: 15( 3)Fuzzy Logic and Neural Networks Based Expert Systems in Chemical Process Systems
- *Correspondence:
- Vijayaraghavan G Chemical Engineering, Rajalakshmi Engineering College, Thandalam, Chennai, Tamilnadu, India
Tel: +91 9865220987; E-mail: vijayaraghavan.g@rajalakshmi.edu.in
Received Date: May 09, 2017 Accepted Date: July 07, 2017 Published Date: July 12, 2017
Citation: Jayalakshmi M, Vijayaraghavan G. Fuzzy Logic and Neural Networks Based Expert Systems in Chemical Process Systems. Int J Chem Sci. 2017;15(3):156
Abstract
Recently planning and functioning of a Chemical Process Systems (CPS) has become more essential and many sophisticated tools were used. In this article, the application of fuzzy logic and neural network based expert systems in CPS was discussed. A brief discussion on fuzzy set theory and its characteristics were presented. Also, the importance of knowledge based expert system on CPS to attain extreme production and high safety was sketched. It was observed that there are several expert systems biased only on fuzzy logic and neural networks; hence it is recommended that the fuzzy logic and neural networks based expert systems in chemical process systems will be an efficient one. The detailed components and its interactions of the classical expert systems were discussed.
Keywords
Fuzzy logic; Neural networks; Expert systems; Chemical process
Introduction
The idea fuzzy logic was first introduced during 1965 by Lotfi A Zadeh, a Professor of computing discipline at the University of California at Berkeley. Predominantly, fuzzy logic is a multivalued logic that supports transitional values to be determined among standard estimations like true or false, yes or no, high or low, etc. Zadeh introduced fuzzy as a means of representing and manipulating data that was not precise, but rather fuzzy [1].
Concepts like relatively hot or cold in most of the chemical processes can be expressed mathematically and managed by computers, in view to relate almost human way of intelligent in the encoding of processors. Fuzzy logic has been developed as a gainful tool for the regulatory and navigating of process systems and multifaceted engineering procedures, as well as for domestic and entertaining electronics, as well as for additional expert systems and other process modelling systems [2].
Nonlinear control is one of the major challenges in contemporary control system. Conventionally, a nonlinear process has to be linearized first before a programmed controller can be successfully applied. This is characteristically attained by tallying a converse nonlinear function to compensate for the nonlinear performance so the overall procedure input-output connection becomes slightly linear. The matter come to be more difficult if a nonlinear characteristic of the system deviations with time and there is a need for an adaptive deviation of the nonlinear performance. These adaptive systems are best controlled with approaches of computational cleverness such as neural networks and fuzzy systems. Nevertheless, progresses of neural or fuzzy systems are not insignificant. Neural networks are accomplished of resembling any multidimensional nonlinear functions and as such they can be very beneficial in nonlinear control [3]. After that, till now there was no detailed technique for determination of appropriate neural network architecture. Presently this is an added art than science. Also, the well-known algorithms frequently have complications to converge to solution and this primes to a lot of displeasures and obstructions. As a consequence, several studies were dejected with neural networks. In the case of fuzzy systems, the system concepts and parameters are at ease to describe. Fuzzy systems consume actual important boundaries of the numeral inputs [4].
An artificial neural network is an information handling scheme that has been established as generalization of mathematical model of human understanding (capability of knowing). Most of the expert systems are outlined based on the artificial neural networks and find extensive applications in cataloguing of pictures, signal processing in controllers, voice recognition, intelligent control systems of boilers, commercial forecasting, condition monitoring, process monitoring neuro predicting and design investigation [5,6].
Fuzzy set based methodologies are investigated in operations research such as fuzzy optimization modelling with linguistic variables and also in fuzzy statistical parameter. However, Kalpanapriya and Pandian [7,8] used fuzzy concept for testing ANOVA model with fuzzy data. Also, they introduced a method to test the statistical hypotheses with fuzzy set, analysis of variance for crisp data with membership grades of fuzzy sets, fuzzy hypothesis testing based on linear correlation, a new method to solve two vehicle cost varying fuzzy transportation problem and interval transportation problem [9,10]. These concepts can be used for the optimized procurement of the chemical process equipments like reactors, heat exchangers [11,12]. In the present review, the role of fuzzy logic based expert system in chemical process systems was discussed and also the mechanism involved in the various control systems like pH control were explained. The detailed presentation of the various expert systems available in the market was given.
Fuzzy Set Theory
Fuzzy set theory simplifies the classical set theory in that membership degree of an object to a set is not restricted to integers 0 and 1, but it may possess any value between 0 and 1. By explaining on the concept of fuzzy sets and fuzzy relations, can define fuzzy logic systems (FLS). Generally, FLSs are rule-based systems, which an input is primarily fuzzified and then processed by an inference engine that recovers knowledge in the form of fuzzy rules contained in a rule-base. Fuzzy sets are calculated by fuzzy inference as output of each rule are further composed and defuzzified (i.e., converted from a fuzzy set to a crisp number). The fuzzy logic system is a nonlinear mapping from input to output space [13].
Let X be the space of objects and x be a standard element of X. The conventional set A, A ⊆ X, is well-defined as a collection of elements or objects x ∈ X, such that each element (x) can also have its place or not to the set A. By describing a distinctive (or membership) function for each element x in X, we can characterize a conventional set A by a set of wellordered pairs (x, 0) or (x, 1), which designates x ∈A unlike a conventional set, a fuzzy set states the degree to which a component fits to a set. Therefore, the membership function of a fuzzy set is permitted to have values between 0 and 1 that designate the degree of membership of an element in the specified set [14].
Definition
The fuzzy sets and its membership functions, If X is a group of objects represented commonly by x , then a fuzzy set A in X is defined as a set of systematic pairs
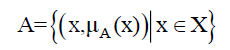
Where 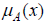 is called the membership function or the fuzzy set A. The membership function maps each element of X to a membership degree between 0 and 1 (included). Clearly, the definition of a fuzzy set is a simple extension of the definition of a traditional (crisp) set in which the characteristic function is permitted to have any value between 0 and 1. If the value of the membership function is limited to either 0 or 1, then A is condensed to a classical set. For simplicity, we shall also mention to traditional sets as normal sets, crisp sets, non-fuzzy sets, or just sets. Typically, X is mentioned to as the universe of discourse, and it may contain of ordered or non-ordered objects or it can be continuous space [15].
is called the membership function or the fuzzy set A. The membership function maps each element of X to a membership degree between 0 and 1 (included). Clearly, the definition of a fuzzy set is a simple extension of the definition of a traditional (crisp) set in which the characteristic function is permitted to have any value between 0 and 1. If the value of the membership function is limited to either 0 or 1, then A is condensed to a classical set. For simplicity, we shall also mention to traditional sets as normal sets, crisp sets, non-fuzzy sets, or just sets. Typically, X is mentioned to as the universe of discourse, and it may contain of ordered or non-ordered objects or it can be continuous space [15].
It is clear that the assembly of a fuzzy set depends on two things: the identification of an appropriate universe of discourse and the requirement of a suitable membership function. The requirement of membership functions is independent, which means that the membership functions quantified for the same notion by dissimilar persons may differ significantly. This bias comes from separate modifications in observing or conveying abstract concepts and has slight to do with randomness. Therefore, the bias and non-randomness of fuzzy sets is the main difference between the study of fuzzy sets and probability theory, which covers the objective treatment of random phenomena [16].
In practice, when the universe of discourse X is a continuous space, we frequently partition it into numerous fuzzy sets whose MFs cover X in a more or less constant manner. These fuzzy sets, which regularly carry names that follow to adjectives looking in our daily language practice, such as “large,” “medium,” or “small,” are called linguistic labels. Thus, the universe of discourse X is often called the linguistic labels. An example on this follows.
Example: Linguistic labels. Suppose that X=“Temperature.” We can define fuzzy sets as “Cold,” “warm” and “hot” which are considered by Membership Functions. Just as a variable can accept various values, a linguistic variable “temperature” can accept different linguistic values, such as “Cold,” “warm” and “hot” in this case. If “temperature” accepts the value of “cold,” then we take the expression as “temperature is cold,” and so forth for the other values.
Fuzzy Rules
During 1973, Lotfi Zadeh circulated subsequent and greatest prominent article, this article defined a novel method to the investigation of complex systems, in which Zadeh recommended taking human like understanding in fuzzy rules. Fuzzy logic propagated out of a need to measure rule-based systems. Rule-based reasoning is grounded in qualitative knowledge representation, and fuzzy logic allows us to mesh a quantitative approach with the qualitative representation. It provides a way to quantify certain qualifiers such as approximately, often, rarely, several, few, and very [17].
The fuzzy rule is able to be well-defined as a qualified statement in the form like:
IF x=A
THEN y=B
Where x and y are linguistic variables; and A and B are linguistic values was founded by fuzzy sets on the universe of discourses X and Y, respectively.
The dissimilarity among traditional and fuzzy rules are a classical “IF-THEN” rule habits binary logic, for example,
Rule 1
IF speed is greater than 100
THEN stopping distance is long
Rule 2
THEN stopping distance is short
The variable speed can possess slightly numerical value among 0 and 200 km/h, but the linguistic variable stopping distance can take also have value long/short. Further, traditional rules are communicated in the conventional Boolean logic. Though, we can also denote the stopping distance rules in the fuzzy form:
Rule 1
IF speed=fast
THEN stopping distance=long
Rule 2
IF speed=slow
THEN stopping distance=short
At this point the linguistic variable speed too has the range between 0 and 200 km/h, but this range comprises fuzzy sets, such as slow, medium and fast. The universe of discourse of the linguistic variable stopping distance can be between 0 and 300 m and may comprise such fuzzy sets as short, medium and long. Therefore, the fuzzy rules narrate the fuzzy sets. The expert systems based on fuzzy logic combine the rules and accordingly changed the number of rules by at least ninety per cent.
Fuzzy reasoning contains two different portions: assessing the rule originator (the IF part of the rule) and consequence or relating the result to the causing (the THEN part of the rule). In classical rule-based systems, if the rule originator is true, then the resulting is also true. In fuzzy systems, where the originator is a fuzzy statement, all rules fire to some extent, or in other words they fire partially. If the originator is true to some degree of membership, then the resulting is also true to that of same degree [18].
These fuzzy sets provide the basis for a weight estimation model. The model is based on a relationship between a man’s height and his weight, which is expressed as a single fuzzy rule:
IF height is tall
THEN weight is heavy
The value of the output or a truth membership grade of the rule resulting can be assessed openly from a consistent truth membership grade in the originator. This form of fuzzy extrapolation practices a technique called monotonic selection.
In the construction rule, a fuzzy rule can consume several backgrounds, for example:
IF project period is long
AND project staffing is enormous
AND project funding is insufficient
THEN risk is high
IF service is outstanding
OR food is delightful
THEN tip is plentiful
The resulting of a fuzzy rule can also comprise many parts, for example:
IF temperature is hot
THEN hot water is reduced
cold water is increased
In this circumstance, all parts of the resulting are affected correspondingly by the originator. In general, a fuzzy expert system combines not one but numerous rules that designate expert knowledge and play off additionally. The output of each rule is a fuzzy set, but frequently we want to find a single number representing the expert system output. In other words, we want to get an exact solution, not a fuzzy. To obtain a single crunchy solution for the output variable, a fuzzy expert system primarily groups all output fuzzy sets into a single output fuzzy set, and then defuzzifies the resultant fuzzy set into a single number.
Expert System
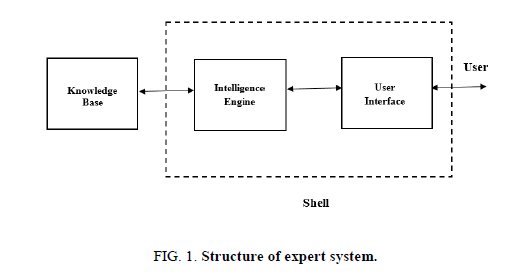
An expert system is a computer program that contains a knowledge base and a set of algorithms or rules that infer new facts from knowledge and from incoming data”. Expert system implements artificial intelligence (AI) to explain constricted and noticeable defined problems and to deliver information in problem solving based on the understanding of experts [19]. Based on this knowledge, a set of rules and certain questions asked the system in capable of making intelligent decisions within its domain and to support the humans in making their decisions. The structure of the expert system is given in Figure. 1.
The greatest innovative application of expert systems (ES) is in the control of certain constraints like pH, flow, level, etc., that define several procedures. In literature, there are quite a few expert systems are presented, in some cases united with other tools like fuzzy logic, etc. Expert Systems are applied for governing certain constraints from a chemical process plant, such as the BIOEXPERT system or for the prime modification of control loops, like “EXPERT_AT” system.
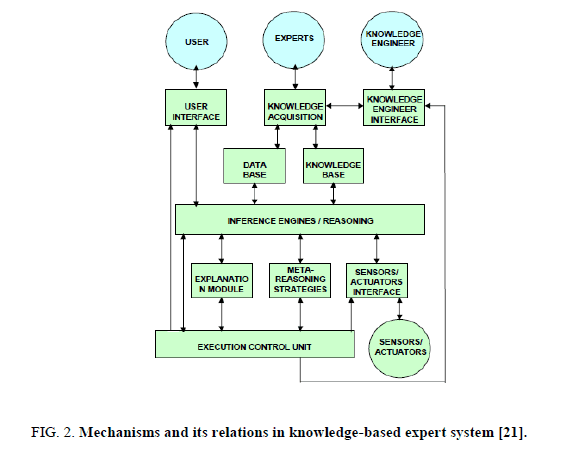
In control system problems, the application of expert system can be executed like a controller. The expert systems instigated as controllers are, from theoretical point of view, alike to fuzzy controllers, but its knowledge base (KB) and inference engine (IE), be able to use additional progressed approaches to regulate which rules will be useful at a certain instant. ES and fuzzy controllers take part in creating the reasonable knowledge which is used the plant operator’s knowledge and proficiency, the fact that it is a main benefit predominantly in the case of multifaceted processes. Logics used in the Expert systems will be of two types, rule based and fuzzy based. The several mechanisms and its relations are explained in Figure. 2.
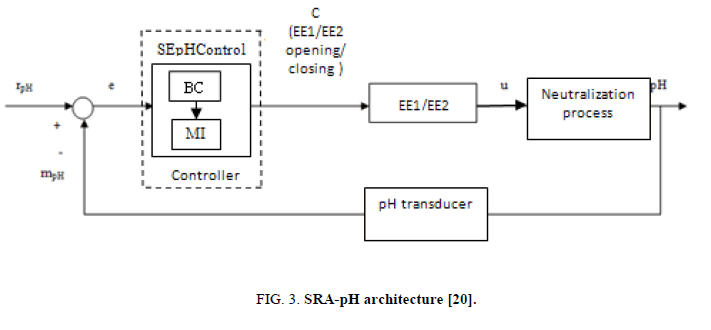
The architecture of the pH control automated system was developed by Carbureanu and it was named as SRA-pH which uses as controller in the developed expert system SEpH Control [20].
From Figure. 3 it was observed that, the components present in the SRA-pH system;
• The controller in the expert system SEpH is in fact the system controller;
• Binary performance elements “EE1and EE2” are used for acid or alkaline counterbalancing dosage;
• The expertise command (C) created by the SEpH Controller, respectively by the EE1 or EE2 opening percentage;
• The prototypical of the counterbalancing process of pH;
• A pH transducer which processes pH value at the process output;
• The error (e) demarcated as the transformation between reference pH value (rpH) and the measured pH value (mpH) at the process output.
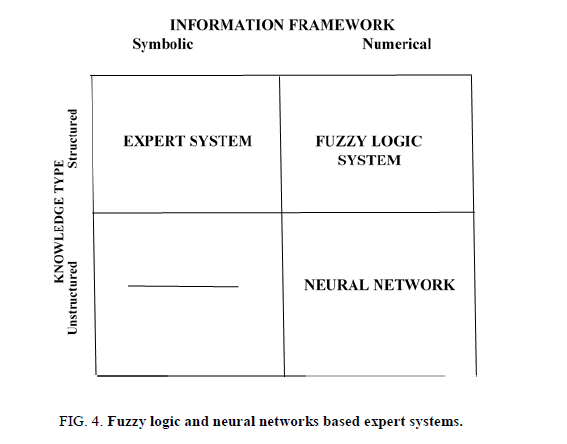
Figure. 4 shows the relationship of fuzzy-logic systems to the two main areas of artificial intelligence (expert systems and neural networks) based on knowledge type and information framework. The knowledge type is divided into structured (based on rules) and unstructured, and the information framework is divided into symbolic and numerical. The varieties of some expert system available in the market are listed in Table 1.
| System | Description |
|---|---|
| DENDRAL | Gathers molecular structure from mass-spectroscopic and nuclear-resonance data (DENDR) algorithm developed at Stanford University. |
| MACSYMA | Accomplishes mathematical manipulation, including symbolic differential and integral calculus, algebra, simplification, limits, and solutions of equations (developed under project MAC at MIT). |
| PROSPECTOR | Supports geologists in their search for one deposit. The system takes in field data and estimates the likelihood of locating a specific type of deposits (developed by SRI International). |
| MYCIN | Detects and recommends treatment for various infectious blood diseases. The system identifies the infecting organism based on symptoms, laboratory data, and patient history. It recommends drug type and dosage for treatment (developed at Stanford University) |
| FALCON | Categorizes the causes of disturbances in a commercial chemical plant. From plant data, FALCON identifies probable sources of disturbances that affect plant performance (Fault Analysis Consultant, developed as a joint project between the University of Delaware, EL DuPont de Nemours, and Foxboro on DuPont’s Victoria, Texas adipic acid plant). |
| ISA | Helps in scheduling customer orders of computer equipment. The system inputs customer orders and develops a schedule based on the current material allocation. It also exposes difficulties and recommends alternatives (Intelligent Scheduling Assistant, developed by Digital Equipment Corporation, and used in their manufacturing facilities.) |
Table 1. Variety of expert systems [22].
The expert systems find more applications in chemical process systems to increase the reliability, to avoid complexity, to develop a rapid technology and for the stable design operations. Expert systems find wide applications in science and engineering area, expert system have gone commercial in several of these listed areas. The detailed list is given in Table 2.
| Process design and planning | Start up and shut down analysis |
|---|---|
| Process plant lay out | Flexibility and reliability analysis |
| Process control, simulation and optimization | Risk assessment |
| Process integration | Process automation and monitoring |
Table 2. Expert system applications in chemical process industries. [23].
Neural-Fuzzy Networks for Expert Systems
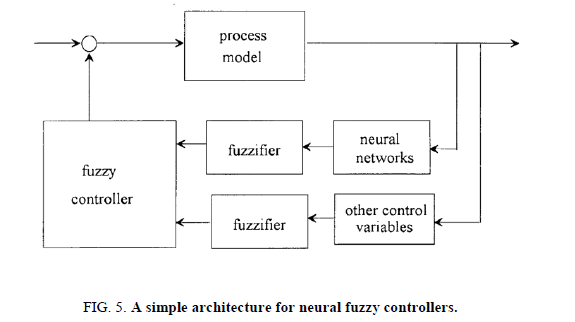
Expert systems require input variables in the form of categorical or fuzzy-logic data. Therefore, the numeric output responses form a neural network must be converted into fuzzy-logic data for the expert system. Figure. 5 shows a typical structure of a neural-fuzzy network used in conjunction with an expert system. Numeric data from a neural network is converted to fuzzy values through a fuzzifier for use as input into an expert system [24]. The expert system produces an output in the form of fuzzy values, which are in turn reconverted to numeric values through a defuzzifier. Note that the output forms the neural network may already be in the form of fuzzy-logic or categorical variables based on the type of network used and may not require a fuzzifier. The defuzzifier may also be unnecessary, depending on what form of output we desire form the expert system [25].
Neural-fuzzy networks for process control
There are three main types of neural-fuzzy networks used for process control. The first uses neural network to predict future responses of a control variable (e.g., cell concentration at the end of a fermentation process), then uses the deviation from the targeted future response to determine the optimal controller settings [26,27]. The final has uses a special neural network structure which functions as a fuzzy-inference system. The neural network predicts either the future response of a control variable or its pattern type, which then becomes the input into the fuzzy-logic controller. A fuzzifier converts the neural network output and any other control input variables that do not require a predictor [28-30]. The fuzzy controller then uses a set of fuzzy rules, similar to an expert system, to obtain the optimal predetermined controller setting.
Representation of fuzzy-logic variables
According to Quantrille et al. [23] it was, noted that fuzzy logic is not a substitute for statistics. Instead, we use fuzzy logic only when statistical reasoning is inappropriate. Statistics expresses the extent of knowledge (or the lack thereof) about a value, and it relies on tools such as variance, standard deviation, and confidence intervals. Fuzzy logic, on the other hand, expresses the absence of a sharp boundary between sets of information [31,32]. For example, using fuzzy logic, we may write:
• Crude oil fractionation is clearly an energy-intensive unit operation, 1.0;
• Thermal cracking is a very energy-intensive unit operation, 0.9;
• Catalytic reforming is a somewhat energy-intensive unit operation, 0.6;
• Catalytic cracking is an energy-intensive unit operation, 0.3;
• Open-air evaporation of brine to produce salt is not an energy-intensive unit operation, 0.0.
Here, the fuzzy logic delineates the lack of a sharp boundary between clearly energy-intensive (1.0) and not at all energy-intensive (0.0). Crude fractionation is very energy-intensive, while open-air evaporation of brine is not at all energy-intensive. Thermal cracking, catalytic reforming and catalytic cracking cannot be considered either very energy-intensive or non-energy intensive. Thus, fuzzy logic does not quantify the lack of knowledge in a statistical sense. Instead, it quantifies the degree or extent of certain words and boundaries between sets of information [33].
To use fuzzy logic, we first need a fuzzy set. In a fuzzy set, the transition from membership to non-membership is not well-defined. We quantify the degree of membership with values between 0 (not a member) and 1 (definitely a member) [34-36]. Additionally, the expert systems are used in Process Safety Analysis (PSA), being a foundation for decision-making practice in chemical industry is a very multifaceted task, on behalf of a number of suspicions linked with information scarcities which may lead to the significant superintending of the safety guarantee of process plant [37,38].
Conclusion
A Knowledge-based judgement on system enhancement certainly a new and intriguing development in chemical process systems and there are many hopes for their better applications in many other fields, including environmental engineering and management. Application o fuzzy and neural network based expert system in CPS is certainly a field where such applications could bring significant improvement in process efficiency, decrease the risk of process failure, and lower capital and operational costs. Apparently, expert systems might upkeep choice and decision-making process already at the stage of plant designing and process selection, and such attempts have been already undertaken as it was described in this paper [39]. The representation of fuzzy logic variable and fuzzy set theory clearly emphasis the relaxed procedure for analyzing the process variables. The idea on the application of neural fuzzy in process control also discussed. A variety of expert systems available was mentioned. Fuzzy logic compromises a diverse way to approach a control problem. This technique emphasis on what the system should do rather than trying to model how it works. One can focus on solving the problem rather than trying to model the system exactly, if that is even possible. In common, the employment of fuzzy logic may be helpful, for multifaceted processes, when there is no simple mathematical model, for extremely nonlinear processes or if processing of the expert knowledge is to be performed. Hence fuzzy logic and Neural Networks based expert systems will run the chemical process systems very effectively.
References
- Zadeh LA. Fuzzy sets. Information and Control. 1965;8:338-53.
- Patry GG, Chapman D. Dynamic modeling and expert systems in wastewater engineering. Lewis Publishers, Chelsea, USA. 1989.
- Zurada JM. Artificial neural systems. PWS Publishing Company, St. Paul. MN, USA. 1995.
- Wilamowski BM. Neural networks and fuzzy systems. In: Mechatronics Handbook, Robert RB, editor. CRC Press, USA. 2002.
- Lapointe J. BIOEXPERT-An Expert System for wastewater treatment processes diagnosis. Comp and Chem Eng. 1989;pp:13-18.
- Kasabov, Nikola K. Foundations of neural networks, fuzzy systems, and knowledge. Eng. 1998.
- Kalpanapriya D, Pandian P. Fuzzy hypothesis testing of ANOVA model with fuzzy data. Int J of Modern Eng Res. 2012;2:2951-6.
- Kalpanapriya D, Pandian P. Two sample statistical hypothesis test for means with imprecise data. Int J Eng Res App. 2012;2:3210-7.
- Kalpanapriya D, Pandian P. Statistical hypotheses testing with imprecise data. App Math Sci. 2012;6:5285-92.
- Kalpanapriya D, Anuradha D. A new method for solving two vehicle cost varying fuzzy transportation problem. Int J Pharm and Technol. 2016;8:16118-24.
- Kalpanapriya D, Pandian P. Two-factor ANOVA technique for fuzzy data having membership grades. Research Journal of Pharmacy and Technology. 2016;9:2394-2402.
- Anuradha D. On solving fuzzy solid assignment problems. Int Res J of Eng and Technol. 2015;2:322-5.
- Nagoor Gani A, Edward Samuel A, Anuradha D. Optimization of air lift operation under fuzzy environment. App Math Sci. 2010;4:2723-32.
- Zadeh LA. The concept of a linguistic variable and its applications to approximate reasoning, part I. Inform Sci. 1975;8:199-249.
- Zadeh LA. The concept of a linguistic variable and its applications to approximate reasoning, part II. Inform Sci. 1975;8:301-57.
- Zadeh LA. The concept of a linguistic variable and its applications to approximate Reasoning, part III. Inform Sci.1975;9:43-80.
- Zadeh LA. Knowledge representation in fuzzy logic. An introduction to fuzzy logic Applications in Intelligent Systems, Kluwer Academic Publishers, Boston.1992;pp:1-26.
- Zadeh LA. Fuzzy logic, neural networks, and soft computing. Communications of the ACM, 1994;37:77-84.
- Zadeh LA, Kacprzyk J. Fuzzy logic for the management of uncertainty. John Wiley, New York. USA. 1992.
- Fedra K, Winkelbauer L, Pantulu VR. Expert systems for environmental screening. An application in the lower mekong basin. International Institute for Applied Systems Analysis, Laxenburg, Austria. 1991.
- Sanchez-Mara? M, Cortés U, Lafuente J, et al. Knowledge-based techniques in wastewater treatment plant management, Encyclopedia of Life Support Systems. 1995.
- C?rbureanu M. Expert system for assessing the effluent’s quality of a wastewater treatment plant, Petroleum-Gas University of Ploiesti. 2010.
- Quantrille Y ,Thomas E, Liu A. Artificial intelligence in chemical engineering, Academic Press, USA 1991.
- Tzafestas S. Expert control systems. Robotics and automation. 2012;17:1-10.
- Ceccaroni L. Integration of a rule-based expert systems, a case-based reasoner and an ontological knowledge-base in the wastewater domain. 2nd ECAI Workshop on Binding Environmental Sciences and Artificial Intelligence, Berlin, Germany. 2000;8:1-8.
- Gimeno JM, Sanchez-Mara? M, Béjar J, et al. Modelling WWTP dynamics by means of transition networks. ECAI’98 Workshop on Binding Environmental Sciences and Artificial Intelligence (BESAI’98). Brighton, U.K. 1998;pp:109-16.
- Gibert K, Roda IR. Identifying characteristic situations in wastewater treatment plants, ECAI’2000 14th Biennial European Conference on Artificial Intelligence, Berlin, Germany. 2000;pp:20-5.
- Loetscher T. SANEX-A simple expert system for evaluating sanitation systems in developing countries. Eco Eng Newsletter. 2000;pp:1.
- Paraskevas PA, Pantelakis IS, Lekkas TD. An advanced integrated expert system for wastewater treatment plants control. Knowledge-Based Systems. 1999;12:355-61.
- Chang AM, Hall LO. The validation of fuzzy knowledge-based systems, fuzzy logic for the management of uncertainty, John Wiley, New York. 1992;589-604.
- Zimmermann HJ. Fuzzy sets, decision-making and expert systems. Kluwer Academic Publishers, Boston, USA 1987.
- Zimmermann HJ. Fuzzy set theory and its applications, 3rd edn. Kluwer Academic Publishers, Boston, USA.1996.
- Baughman DR, Liu YA. Neural networks in bioprocessing and chemical engineering. Academic Press, USA. 2014.
- Agrawal M, Jade AM, Jakaraman VK, et al. Support vector machines: A useful tool for process engineering applications, CEP. 2003;57-62.
- Sanchez E. Fuzzy logic and inflammatory protein variations. Clinica Chimica Acta. 1998;270:31-42.
- Sanchez E, Bartolin R. Fuzzy inference and medical diagnosis: A case study. J Bio Fuzzy Sys Assessm. 1990;1:4-21.
- Sarmasti Emami MR. Fuzzy logic applications in chemical processes. J Math and Comp Sci. 2010;1:339-48
- King PJ, Mamdani EH. The application of fuzzy control system to Industrial processes. Automatica. 1997;13:235-42.
- Vijayaraghavan G, Jayalakshmi M. Fuzzy logic in process safety modeling of chemical Process. Int J Adv Eng Res and Studies. 2013;2:118-21.