Review
, Volume: 18( 2)Character of the Representative Permutation as a Tool of Stereoisomers Counting: Application to the Permethrinic Acid
- *Correspondence:
- Issofa Patouossa
Department of Physical and Theoretical Chemistry, University of Yaounde, Yaounde, Cameroon
Tel: 693181788
E-mail: patouossa12@yahoo.fr
Received: November 24, 2022, Manuscript No. TSPC-22-81003; Editor assigned: November 28, 2022, PreQC No. TSPC-22-81003 (PQ); Reviewed: December 12, 2022, QC No. TSPC-22-81003; Revised: February 25, 2023, Manuscript No. TSPC-22-81003 (R); Published: March 06, 2023, DOI: 10.37532/0974-7524.2023.18(1).001
Citation: Patouossa I, Njabon EN, Kabuyayab BI, et al. Character of the Representative Permutation as a Tool of Stereoisomers Counting: Application to the Permethrinic Acid. Phys Chem Ind J. 2023;18(1):001.
Abstract
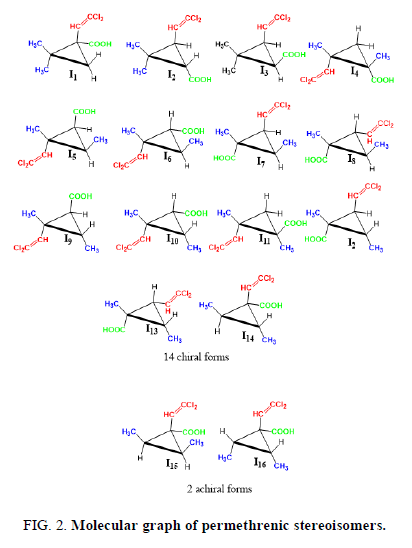
A combinatorial counting using the character of the representative permutation approach has been carried out on the permethrenic acid in order to determine the exact number of his chiral and achiral stereo isomers having the empirical formulae C3H2X2YZ; where X, Y and Z, stand respectively for the methyl, the diclhorovinyl and the carboxyl groups. We have shown that permethrenic acid presents sixteen stereoisomers, divided into fourteen enantiomeric pairs or chiral forms of C1 symmetry and two achiral forms belonging to Cs’ point group.
Keywords
Character; Representative permutation; Permethrenic acid; Chiral; Achiral; Stereoisomers
Introduction
Permethrenic acid is known as one of the precursors of permethrin having weak insecticidal activity used in the agricultural and veterinary fields [1,2]. It is an organ chlorine compound derived from carboxylic cyclopropane [3,4].
Given the different positions that the methyl, dichlorovinyl and carboxyl groups may occupy on the cyclopropane skeleton, several stereoisomers of this compound can be generated and some of them already exist in nature. In order to evaluate the biological activity of this compound in relation to its structure, it is necessary to know the exact number and structure of its different stereoisomers.
Therefore, the character of permutations used in the combined formalism of Fowler and Shao can be used to enumerate the stereoisomers of this compound [5,6]. This formalism allows the examination of permutations of different substitution sites on the basic skeleton or parent molecule. The contributions of the different symmetry operations of the point group of the parent molecule are grouped into subgroups of permutations allowing to characterize the listed derivatives and to split them into chiral or achiral isomers.
Literature Review
Computational details
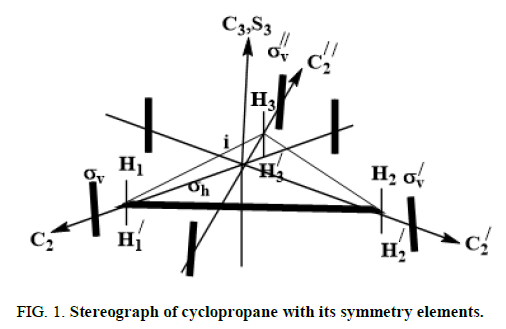
Symmetry of parent molecule: Let us consider the stereograph cyclopropane shown in Figure 1 as the parent building block.
This stereograph belongs to D3h point group and exhibits 12 symmetry elements/operations listed in equation 1
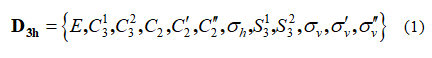
These symmetry operations are partitioned into 6 equivalence classes given in equation 2 here after:
E, 2C3, 3C2, δh, 2S3, 3δv (2)
This latter gives rise to 10 non-redundant subgroups comprising 4 chiral subgroups and 6 achiral subgroups shown in Table 1.
| Subgroup | Symmetry operations | Chirality |
|---|---|---|
| C1 | E | Chiral |
| C2 | E, C2 | Chiral |
| Cs | E, σh | Achiral |
| Cs | E, σv | Achiral |
| C3 | E, C¹3, C²3 | Chiral |
| C2v | E, C2, σh, σv | Achiral |
| C3v | E, C¹3, C²3, σv, σ'v, σ''v | Achiral |
| C3h | E, C¹3, C²3, σh, S¹3, S²3 | Achiral |
| D3 | E, C¹3, C²3, C2, C'2, C''2 | Chiral |
| D3h | E, C¹3, C²3, C2, C'2, C''2, σh, S¹3, S²3, σv, σ'v, σ''v | Achiral |
TABLE 1. Subgroups of D3h.
Fowler’s approach: The application of symmetry operations on a parent molecule generates permutations from which we can find representative permutation associated with the movements of atoms (Table 2).

| Symmetry operation | Generated permutations | Γσ | Γ²σ | Γ³σ | [Γ²σ] |
|---|---|---|---|---|---|
| E | (H1)(H2)(H3)(H'1)(H'2)(H'3) | 6 | 36 | 126 | 21 |
| C¹3 | (H1H3H2)(H'1H'3H'2) | 0 | 0 | 0 | 0 |
| C²3 | (H1H2H3)(H'1H'2H'3) | 0 | 0 | 0 | 0 |
| C2 | (H1H1')(H2H2')(H3H3') | 0 | 0 | 0 | 0 |
| C'2 | (H1H'3)(H2H'2)(H2H'2) | 0 | 0 | 0 | 0 |
| C''2 | (H1H'2)(H2H1')(H3H'3) | 0 | 0 | 0 | 0 |
| σh | (H1H'1)(H2H'2)(H3H'3) | 0 | 0 | 0 | 0 |
| S¹3 | (H1H'3H2H'1H3H'2) | 0 | 0 | 0 | 0 |
| S²3 | (H1H'2H3H'1H2H'3) | 0 | 0 | 0 | 0 |
| σv | (H1)(H2H3)(H'1)(H'2H'3) | 2 | 4 | 8 | 5 |
| σ'v | (H1H3)(H2H'2)(H'1H'3) | 2 | 4 | 8 | 5 |
| σ''v | (H1H2)(H3)(H'1H'2)(H'3) | 2 | 4 | 8 | 5 |
TABLE 2. Generated permutations and reductible representation.
Reductible representation for quadruple replacement of type X2YZ

Coset representation

Results and Discussion
Characters of ΓX2YZ
The application of equation 4 allows us to obtain characters of the reducible representation ΓX2YZ under each class of equivalent symmetry operation shown in the following Table 3.
| E | 2C3 | 3C2 | 2S3 | σh | 3σv | |
|---|---|---|---|---|---|---|
| ΓX2YZ | 180 | 0 | 0 | 0 | 0 | 4 |
TABLE 3. Characters of ΓX2YZ
ΓX2YZ can be expressed as sum of irreducible representation of the parent group. Using equation 8, one can show that:
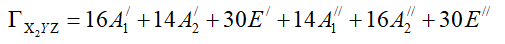
The multiplicity of the totally symmetric irreducible representation of D3h is the total number of stereoisomers of C3H2X2YZ. In the present situation this number is equal to 16 because A'1 is totally symmetric irreducible representation of D3h.
From the correlation table of D3h point group one can show that:
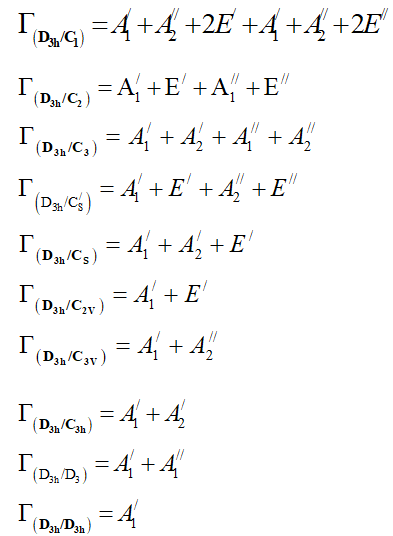
From equation 7 we deduce that:
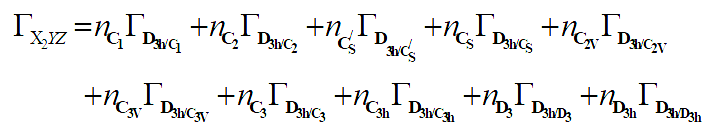
The corresponding linear system is given as follow:
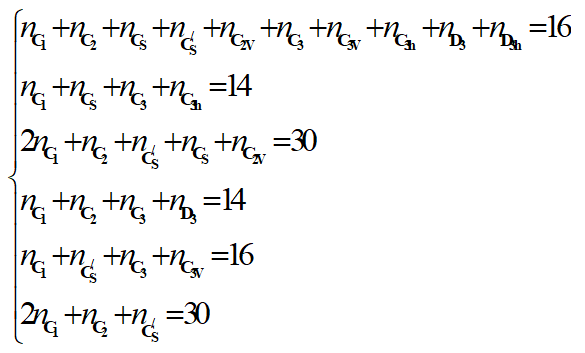
Notice that it is not possible to find the exact solution of this linear system of 6 equations with 10 unknowns. Fortunately some of them can be predefine by the geometry of the molecule and the type of substitution [7,8].
For instance any heterosubstitution on the cyclopropane skeleton cancel the C2, C3 axis and σh symmetry elements. As a result all the subgroups containing these 3 elements plane consequently every subgroup containing these 3 elements namely CS,C2,C2V,C3,C3V,C3h,D3,D3h will disappear.
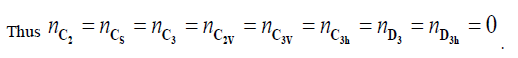
The linear system of 6 equations can be reduce as follow:

The permethrenic acid generates simultaneously 14 enatiomeric pairs or chiral form with the C1 symmetry and 2 achiral forms belonging to C's group. The Figure 2 shows the molecular graph of the sixteen stereoisomers of permethrenic acid (Figure 2).
Conclusion
The enumeration of stereoisomers of permethrenic acid symbolized by the empirical formula the empirical formulae C3H2X2YZ; where X, Y and Z and symbolizes respectively the methyl, the dichlorovinyl and the carboxyl groups using character of the representation has been carried out. We have 14 chiral form which possess the C1 symmetry and 2 achiral forms belonging to C'S group. We can also notice that in this family of compound the chiral forms are predominant.
References
- Mirzabekova NS, Kuzmina NE, Lukashov OI, et al. Synthesis and biological activity of permethrinic acid analogs containing various substituents in position 2 of the cyclopropane ring. Russ J Org Chem. 2008;44:1139-1149.
- Naumann K, Synthetic pyrethroid insecticides: Structure and properties. 1st Edition, Springer, Softcover Reprint of the Original, Germany. 1990.
- Kaufman DD, Hayes SC, Jordan EG, et al. Permethrin degradation in soil and microbial cultures. Syn Pyr. 1977;147-161.
- Sharom MS, Solomon KR. Adsorption desorption, degradation and distribution of permethrin in aqueous systems. J Agric Food Chem. 1981;29(6):1122-1125.
- Fowler PW. Isomer counting using point group symmetry. J Chem Soc. 1995;91(15):2241-2247.
- Shao Y, Wu J, Jiang Y. Enumeration and symmetry of substitution isomers. J Phys Chem. 1996;100(37):15064-15067.
- Atkins PW, Child MS, Phillips CSG. Tables for Group Theory. Oxford University Press, United Kingdom. 1970.
- Altmann SL, Herzig P. Point Group Theory Tables. Oxford University Press, United Kingdom. 1994.