Original Article
, Volume: 15( 4)Modeling Kinetics and Transport Phenomena during Multi-Stage Tire Wastes Pyrolysis
- *Correspondence:
- Khiari B , Environment Science and Technology Research Laboratory, High Institute of Environment Sciences and Technologies of Borj Cedria, Hammam Lif, Tunisia, Tel: +21671749100; E-mail: besmakhiari@yahoo.com
Received: May 24, 2017; Accepted: November 15, 2017; Published: November 18, 2017
Citation: Khiari B, Kordoghli S, Mihoubi D, et al. Modeling Kinetics and Transport Phenomena During Multi-Stage Tire Wastes Pyrolysis. Int J Chem Sci. 2017;15(4):221
Abstract
This paper is devoted to the modeling of the pyrolysis process in order to predict mass and heat loss profiles of a used tire sample. After making certain assumptions, the thermal balances and kinetics of each reaction were written. The resolution of the differential equations allowed us to present the profile of heat variation within the sample as a function of time. The conversion of the reaction was also modeled and compared with that obtained experimentally. There is a satisfactory agreement between the theoretical and the experimental results. The modeling is based on the energy behavior of each reaction and showed in particular that certain exothermic reactions intervene during the pyrolysis of the used tires.
Keywords
Tire waste; Simulation; Model; Exothermic reaction; Heat and mass transfer
Introduction
The kinetics of the pyrolysis reaction is characterized by several parallel and serial reactions (in solid and gaseous phases) involving several chemical mechanisms such as bond rupture, dehydrogenation, cyclization, etc. Today, a major step in the pyrolysis process is the intensification of the use of pyrolysis reactors, for which a kinetic model must be appropriately maintained, in order to describe the complexity of the processes that occur during the thermal degradation of large polymer chains. In addition, this model should be easy to handle when implementing the design stages of an industrial reactor. A presentation of the literature concerning the modeling of the pyrolysis process of used tires shows that these studies can be classified according to the type of reaction scheme chosen, namely reaction mechanisms in one step or in several stages. Most of these studies admit that the pyrolysis reaction is endothermic and does not take into account exothermic reactions. It is also noted that the envisaged thermal balances did not integrate the energy contribution of the exothermic reactions. Therefore, the model developed in this work has been designed to represent the loss of mass and heat profiles using thermal phenomena and kinetics of exothermic reactions. In a first step, the equations of the different heat transfer and mass transfer processes were initiated. Then, the first simulations of these different transfer phenomena are exposed.
Previous work
The bibliographical analysis indicates that many works are devoted to the study of pyrolysis mechanism taking into account thermal degradation of used tires. However, the approach chosen by the authors differs.
Some have chosen to develop models that show one-step reaction patterns [1-5], while others propose multi-reaction schemes [6-13]. Whatever the model, several assumptions are commonly made. They relate to the sample and its properties as well as to heat transfer and diffusion during the process.
Furthermore, during the pyrolysis, the raw material is decomposed, at a temperature up to 600°C and in anaerobic conditions, into three products: char, condensable gas and non-condensable gas. The yield and chemical composition of these three products are governed by the kinetics of the pyrolysis reaction. In addition, yields and chemical composition can be varied by adjusting the pyrolysis conditions, in order to promote certain reactions.
Experimental
Most kinetic studies have been carried out in thermogravimetric equipments [14-16], which allows the evolution of the mass of the polymer to be monitored throughout its degradation under isothermal/non-isothermal conditions. Indeed, thermogravimetric analysis (TGA) and its derivative (DTG) are common techniques for measuring the kinetics of mass loss, which is induced by the evaporation of pyrolysis products.
The process of pyrolysis of tire wastes has been studied in detail using numerous approaches by various researchers over the decades in order to understand its kinetics and its reaction mechanisms [17-19]. A popular approach to reach a better understanding is to develop appropriate mathematical models and reaction patterns. Different models have been used, including kinetic models, mass transfer models, heat diffusion models, etc.
We can cite some works on the development of a mono-reaction model, such as Quek and Balasubramanian [18]. Their study is based on experimental investigation to identify the different components of tires, mainly oils, natural rubber (NR) and synthetic rubber (BR and SBR). Each of these components follows the Arrhenius equation assuming that the reaction is first order. Thus, the proposed approach consists of modeling each major component separately.
Furthermore, in order to maximize the desired products and minimize the solid residue, Al-Salem et al. [20] undertook a kinetic approach to evaluate the reaction rate constants, assuming that the product is based on a first order thermal cracking reaction. They presented the scheme according to which the polyisoprene (PI) of used tires can be converted into aromatic fractions [A], liquid [L], gas [G] and solid residue [C], with the corresponding rate constants K1, K2, K3 and K4 respectively. On the other hand, the reactions of the liquid in aromatic fractions [A] and in gas [G] with K5 and K6 rate constants respectively are presented.
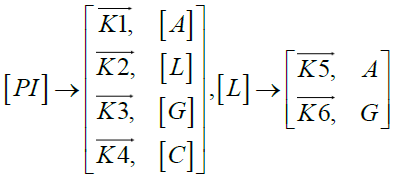
These reactions can be expressed by the following equations:
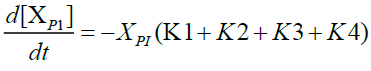 (1)
(1)
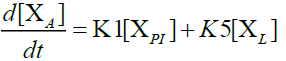 (2)
(2)
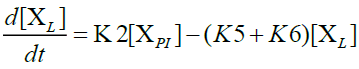 (3)
(3)
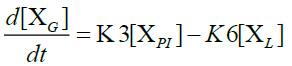 (4)
(4)
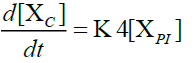 (5)
(5)
The fractions of used tires (represented by PI), aromatics, liquid, gas and char are XPI, XA, XL, Xg et Xc respectively. The thermal cracking scheme proposed was based on the yields of the products which they classified into 4 categories: gas (C1- C4), liquid (non-aromatic, C5-C10), monocyclic aromatic fractions (C5-C10) and solid residue.
Other authors have taken up this study and confronted it with experimental results. It emerges that the tire components are involved in the mass loss reaction differently. This is why they proposed reaction schemes as a function of the components identified by the peaks in the TGA curve and for which the Arrhenius equation can be applied [20-23]. Indeed, it is generally accepted that the different zones that can be distinguished in the devolatilization thermogram are attributed to the different components of the tire [24-27]. These different components break up independently of each other, with little interaction. The non-dependence of the thermal decomposition of the polymer is the basis for the construction of most used tire pyrolysis models.
Moreover, the wide variety of compounds generated during the pyrolysis of polymer materials makes it difficult to propose a rigorous kinetic scheme to describe the formation of individual compounds. Consequently, approximations have been used in the literature to study the pyrolysis kinetics, the most common being the pseudo-mechanism and its adjustment with the experimental data to determine the unknown parameters. The modeling of tire pyrolysis kinetics gives an overview of the mechanisms which are responsible of the decomposition process and predicts the potential difficulties in the pyrolysis reactor. On this basis, the pyrolysis reaction must be presented in the form of multiple reactions in order to better understand the degradation mechanism. Thus, other models, which may be called multi-reaction, have been proposed. The first ones, to develop such a model, are probably Senneca et al. [28] in the thermogravimetric study with high heating rates. The scheme is built upon 4 reactions in series and in parallel as shown below:
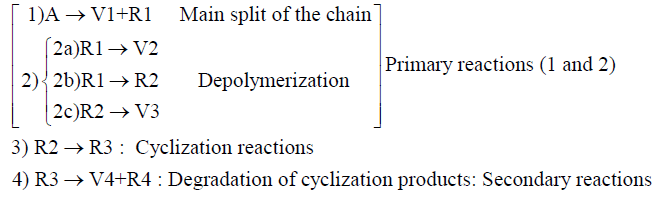
A represents a typical molecule of the organic chain of the tire polymeric components. The molecule A would be a butadiene monomer sequence in the case of PBR (polybutadiene rubber), a butadiene block and styrene monomers in the case of SBR (styrene-butadiene rubber). It is assumed that the first step shows the cleavage of the original chain A. This occurs with the formation of an intermediate R1 and with limited generation of volatiles V1. The intermediate can depolymerize directly via the pathway (2a) with volatile emission, or it can be transformed into a second intermediate R2 (2b) and subsequently depolymerizes with the release of volatiles V3 (2c).
Reactions 1, 2a, 2b and 2c are presented together in order to carry out the primary reactions of the pyrolysis. An extremely important step involves the cyclization of the radical intermediate product R2 through reaction 3. This path, which competes with the depolymerization, prospects a more stable residue (R3). Then and only for high temperatures, this residue degrades, thus generating the final product R4 and other volatile materials V4. Reaction 4 therefore represents the secondary reaction.
This system integrates the mechanism proposed by Golub and Gargiulo [29] for the depolymerization of polybutadiene. According to these authors, the volatiles in the primary reactions (V1) are not present. The proposed scheme is representative of the thermal degradation of PBR (polybutadiene rubber) and SBR (styrene butadiene rubber).
When degradation of natural rubber is considered, the proposed scheme can be compared with the mechanism suggested by Bhowmick et al. [30]. This scenario agrees with that of Brazier and Schwartz [31]. The opinion of a two-stage pyrolysis mechanism is also supported by the results of Atal and Levendis [32]. A simplified Van de Vusse type scheme [28] has been presented by simplifying the previously reported model by grouping the primary steps of the pyrolysis into a single reaction pathway:
1. A→V1 Primary reaction
2. A→R Cyclization reaction
3. R→V2 Degradation of cyclization products
This type of multi-reaction model was taken up by Cheung et al. [33] by highlighting the effect of the involved exothermic and endothermic reactions. Other multi-reaction models have been proposed. Mention may in particular be made of those of Yang and Roy (1996) [34] and Oyedun et al. [35]. All of these models have been widely used within the research community to examine the technical viability of pyrolysis of used tires [36-38].
Modelling
As mentioned above, works on the modeling of pyrolysis can be classified according to the type of reaction scheme chosen. Some authors contemplate pyrolysis according to a one-step reaction mechanism, while others propose several steps with consecutive reactions. It would seem that this latter type of model leads to better matching with the experimental results. On the other hand, most of these models often consider pyrolysis as an endothermic process. From an experimental point of view, the measurement of the temperature evolution of the sample during its pyrolysis led other researchers to define the pyrolysis process as a set of endothermic and exothermic reactions [35,36].
The model developed in this work aims to present the profile of mass loss and temperature during pyrolysis using endothermic and/or exothermic phenomena and reaction kinetics. This model should also make it possible to represent the temporal variation of the enthalpy of the total reaction. Thus, the reaction scheme adopted in the framework of this work is first defined. Then, the different equations related to the mass and heat balances as well as the initial and boundary conditions are presented. Finally, the validity of the model is evaluated by comparison with experimental results.
Reaction Scheme
Pyrolysis is an overall endothermic process that begins exothermic with the cracking of organic matter into small fractions. When the processing temperature is high, some of the primary products are cracked into by-products and will be vaporized. The reaction scheme adopted is set out below:
Reaction 1: TA → Volatiles (V) + Char (C)
Reaction 2: Rubber → Intermediate A (IA)
Reaction 3a: Intermediate A (IA) → Volatiles (V) + Char (C)
3b: Intermediate A (IA) → Intermediate B (IB)
3c: Intermediate B (IB) → Volatiles (V) + Char (C)
The organic additives of tires (TA) are subjected to pyrolysis to produce volatiles (V) and char (C) (Reaction 1). The rubber of the tire follows the reaction (2) to carry out the cleavage of the main chain in order to obtain an intermediate (IA). This product (IA) can be depolymerized directly to form volatile compounds (V) and char (C) (Reaction 3a), or it may be cracked to form shorter organic chains as an intermediate (IB) (reaction 3b). The intermediate (IB) would then be finally pyrolyzed to form volatiles (V) and char (C) (Reaction 3c).
Mass transfer balance
The modeling of tire pyrolysis is based almost exclusively on the TGA and DTG data. Typically, the thermo-grams show the percentage of the mass loss with respect to time or temperature [9]. The modified Arrhenius law is currently the most widely used model to represent the loss of mass and its rate during the degradation of solids subjected to heat flux. The model includes the kinetics of endothermic mass loss and exothermic cracking reactions. In the proposed mechanism, reactions 1, 3a and 3c are mass loss reactions which contribute to endothermic kinetics and reactions 2 and 3b refer to cracking exothermic kinetics.
All endothermic reactions follow the Arrhenius model:
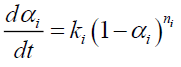 (6)
(6)
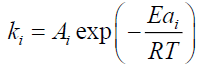 (7)
(7)
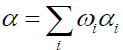 (8)
(8)
Where,
αi: Mass loss conversion of reaction I;
α: Total mass loss fraction;
ωi : Contribution coefficient to mass loss due to reaction I;
ki : Rate constant of reaction i (s);
Ai : Pre-exponentiel factor (s-1);
Eai : Activation energy (J/mol);
ni : Ordre of reaction I;
R : Gas constant (J/mol K);
T : Temperature (K);
t : Time (s).
The kinetic parameters (Ai, Eai, ηi) and mass loss contributions (ωi) can be deduced by adjusting the mathematical model (equations 6-8) with the experimental TGA/DTG results. In the case of non-isothermal pyrolysis, it would be better to present the experimental data by expressing the variation of the mass loss as a function of the variation in temperature. The 6 becomes:
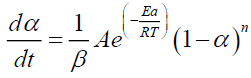 (9)
(9)
Where, β is the heating rate (°C/min).
A linearized form of the differential equation (V.1) can be used in the following form:
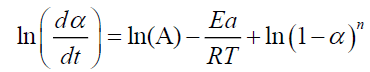 (10)
(10)
For n=1
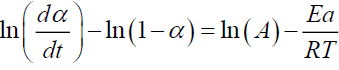 (11)
(11)
Plotting  gives Ea and A.
gives Ea and A.
The same procedure is followed for the resolution of equation (V.4) such that:
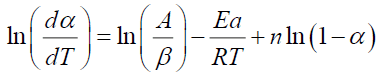 (12)
(12)
The main difference in the several models of tire pyrolysis is the approximation method for obtaining Ea and A. For the models presented above, which are used to describe the pyrolysis of used tires, three main assumptions are required:
• The main components of the tire (processing oils, polybutadiene, and styrene-butadiene copolymer) thermally decompose independently of one another without any interaction between them.
• Each of these decomposition reactions follows a single mechanism that is irreversible.
• Only DTG curve data is required to estimate initial tire composition (identification of the components and their mass), devolatilization rate of each component and kinetic parameters. Given that the exothermic reactions (decomposition of organic matter into shorter molecular fractions) involved in the proposed kinetics are reactions 2 and 3b, the phenomenon is modeled as follows:
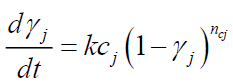 (13)
(13)
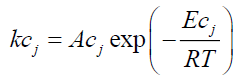 (14)
(14)
Where,
γj: Conversion of the exothermic reaction j;
kcj : Rate constant of exothermic reaction j (s-1);
Acj : Pre-exponential factor of exothermic reaction j (s-1);
Eci : Activation energy of exothermic reaction j (J/mol);
ncj : Order of exothermic reaction j.
Thermal transfer balance
Heat and mass transfers must be integrated into a kinetic model to describe the actual temperature of the tire, during pyrolysis. Heat and mass transfer processes are important because the decomposition of tires during pyrolysis is initially controlled by the rate of heating due to the predominance of surface reactions but becomes more controlled by diffusion in the final stages. The mathematical model that will be presented integrates the kinetics of mass loss and heat transfer. It is built for a single particle of tires that would be pyrolyzed in a batch discontinuous reactor. The process of pyrolysis of used tires involves very complex physicochemical phenomena which are difficult to model very faithfully. Thus several simplifying hypotheses will be proposed:
• The configuration of the reactor is not specified, but it is assumed to be capable of providing suitable conditions (e.g. energy supply, mechanical motions) for pyrolysis.
• The particle is heated by pyrolysis gas by convection inside the reactor.
• The reactor temperature is the same as that of the pyrolysis gas.
• Thermal transfer takes place by conduction and convection.
• The density of the tire particle is assumed to be constant throughout the pyrolysis.
• The volatile pyrolysis products are produced in the reaction zone and they leave immediately.
• The shape of the tire particle is cubic (thickness is negligible).
The above assumptions define the geometry of the tire particle and the heat transfer modes that take place inside the particle. The thermal balance of the tire particle can then be established based on these assumptions. Indeed, the tire particle is divided into multiple layers of control volume. Since heat is applied to the particle externally, the positive heat flux is defined from the surface of the particle to the core. Exothermic reactions contribute with exothermic heat (qexo) to the particle and, on the other hand, the pyrolysis products are vaporized and consume the heat of vaporization (qvap). Sensitive heat (qS) is also involved in thermal equilibrium and can be treated as energy stored inside the control volume and thus affects its temperature.
The heat flows coming in a control volume inside the particle are:
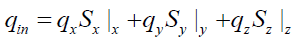 (15)
(15)
The heat fluxes outgoing from the control volume are:
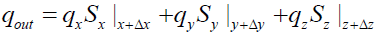 (16)
(16)
Where
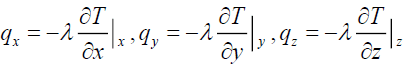
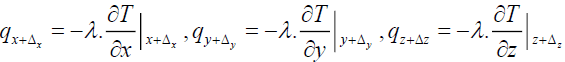 (17)
(17)
The heat flow consumed by vaporization inside the control volume is:
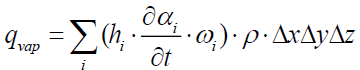 (18)
(18)
The heat flux released by the exothermic reaction inside the control volume is:
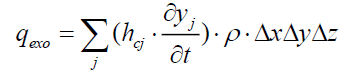 (19)
(19)
The heat flux stored inside the control volume is:
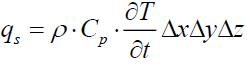 (20)
(20)
Thermal equilibrium is thus:
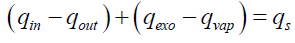 (21)
(21)
By expanding the terms of the above equation we obtain the following equation of heat:
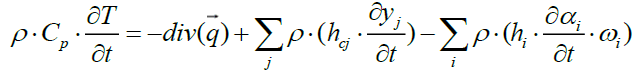 (22)
(22)
In the incoming paragraphs, we will only model a section of the particle following x and y.
As the tire particle is subjected to pyrolysis, the compositions of the tire particle vary. The following equations are used to monitor the consequent change in the thermal conductivity of the particles λ and the heat capacity Cp [33].
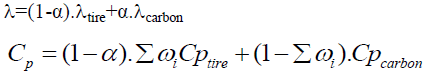 (23)
(23)
To obtain the equation of the specific capacity, several hypotheses have been made:
• Tire waste is assumed to consist of rubber and carbon black only.
• The calorific capacity of rubber is equal to the calorific capacity of the tire (CpRubber=Cptire). The thermal capacity of the tire particle (Cp) is therefore influenced by the amount of rubber and black carbon present in the tire particle.
Initial and boundary conditions
The admitted conditions are:
• T(t=0)=T0: initial temperature
• The transfer of heat between the pyrolysis gas and the particle surface is carried out by convection (boundary condition at the surface of the particle)
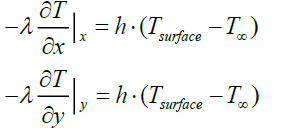 (24)
(24)
Where
T∞ : Reactor temperature (°C)
Tsurface : Particle surface temperature (°C)
h: coefficient of convection between the pyrolysis gas and the particle
• During the pyrolysis, the reactor temperature is increased at a predefined heating rate (β) until the reactor reaches the set point temperature.
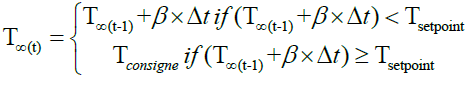 (25)
(25)
The various quantities introduced into the heat and mass balances as well as the equations describing the boundary conditions are summarized in TABLES 1 and 2. These quantities are either derived from the literature, or calculated by analyzes of the graphs of TGA, or even measured according to the case.
| Parameter | Value | Reference |
|---|---|---|
| T∞(t-1) | 25°C | Measured |
| β | 9°C/min | Measured |
| λtire | 0,38 W/mK | [39] |
| λcarbon | 0,20 W/mK | [39] |
| h | 50 W/m2K | [39] |
| Tsetpoint | 550°C | Measured |
| ρ | 1100 Kg/m3 | [39] |
| Cp | 1230 J/KgK | [34] |
| Cpcarbon | 1800 J/KgK | [34] |
TABLE 1. Values of different parameters used in the model.
| Kinetic and thermodynamic parameters | Reaction 1 | Reaction 2 | Reaction 3a | Reaction 3b | Reaction 3c |
|---|---|---|---|---|---|
| Pre-exponential factor A (s-1) | 51,7 | 4,17 106 | 2,52 106 | 9,96 106 | 2,70 107 |
| Activation energy Ea (J/mol) | 61,63 103 | 119,15 103 | 119,42 103 | 130,10 103 | 129 103 |
| Reaction order n | 2,26 | 1,74 | 0,93 | 0,89 | 0,9 |
| Reaction Enthalpy (J/kg) | 480 103 | 42,5 103 | 253,4 103 | 195,5 103 | 701,9 103 |
TABLE 2. Kinetic and thermodynamic parameter values used in the model.
Results and Discussion
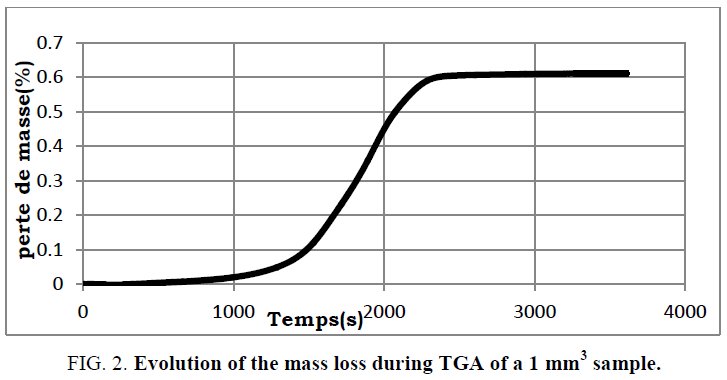
The numerical resolution of the different differential equations of the model was performed using finite element software. This type of resolution makes it possible to carry out a discretization of the differential equations which are then integrated in order to obtain solutions at different times. At the program execution, the user can choose the sample size and the initial and final temperatures of the reaction. The model presented by equation (22) and the initial and boundary conditions have been validated for different samples. The mass loss profiles of a 1 cubic mm sample are measured and compared to the results from the model (FIG. 1 and 2 ).
FIG. 2: Evolution of the mass loss during TGA of a 1 mm3 sample.
The general profile of the conversion as a function of time is similar to that obtained experimentally. Still, there is an offset between the two paces of about 600 s. This is probably due to the difference between the temperature introduced in the model and that actually followed by the reactor which adjusts itself according to the operating conditions of the experiment. The model needs to be refined to better match the experimental results.
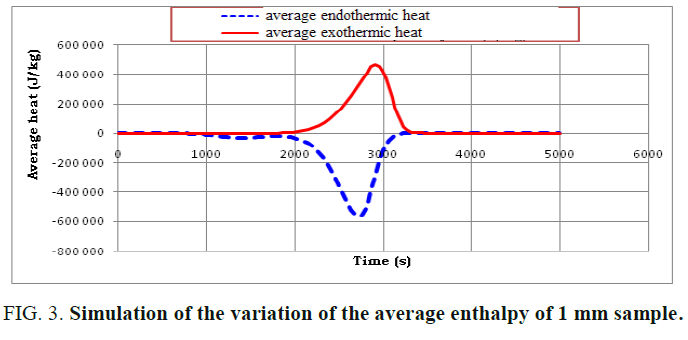
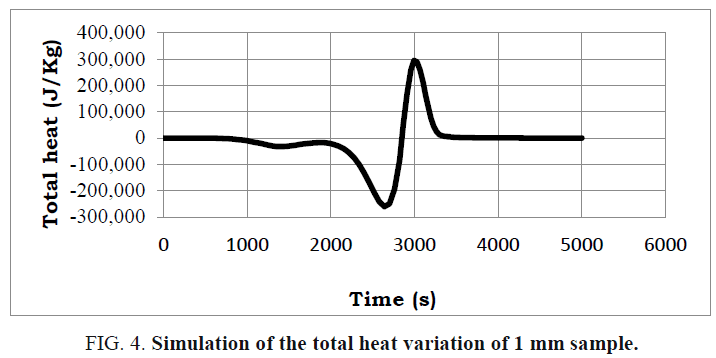
A presentation of the average heat and the total heat during the reaction of the pyrolysis is illustrated in FIG. 3 and 4.
By examining these figures, a good match with the proposed reaction scheme is noted. This is because the reaction of the pyrolysis begins with an endothermic reaction and then with an exothermic reaction which provides the energy necessary to complete the endothermic reaction which thus presents an energy gain for the installation.
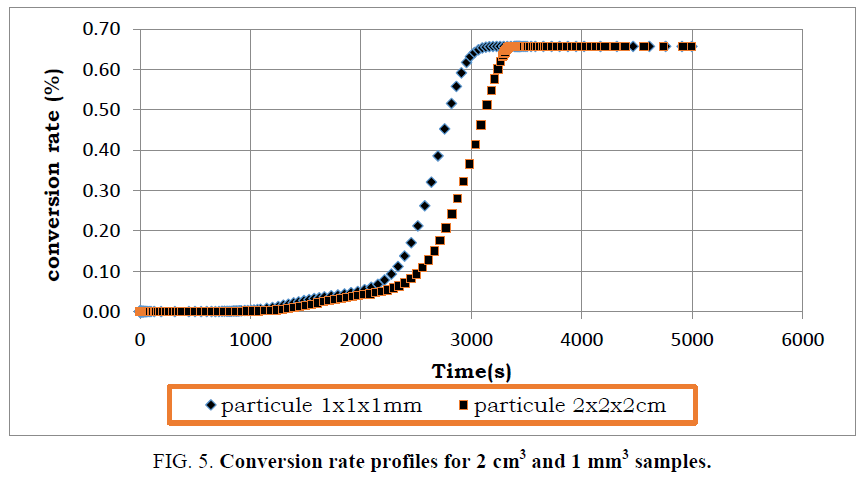
During pyrolysis of used tires, operating parameters such as tire composition, process temperature, heating rate and particle size impact the products of pyrolysis. Some of these parameters have been examined closely, but the particle size of used tires is often neglected. In order to analyze the effect of the particle size on the mass and heat transfer of the pyrolysis reaction, the model was tested for a 2 cm sample size. The mass loss and heat loss profiles of the pyrolysis reaction are compared in FIG. 5 to 8 with those of the 1 mm scale sample.
By comparing the mass loss profiles for the two types of particles, it is logically found that the conversion time of the used tires with dimensions 1 mm is shorter than that recorded with the particle of dimension 2 cm (FIG. 5). This is due to thermal transfer phenomena which are more efficient with small particles. In addition, the reactivity of solid residues increases when the particle size is smaller. Indeed, the heat transfer barrier decreases as the size of the particles becomes smaller.
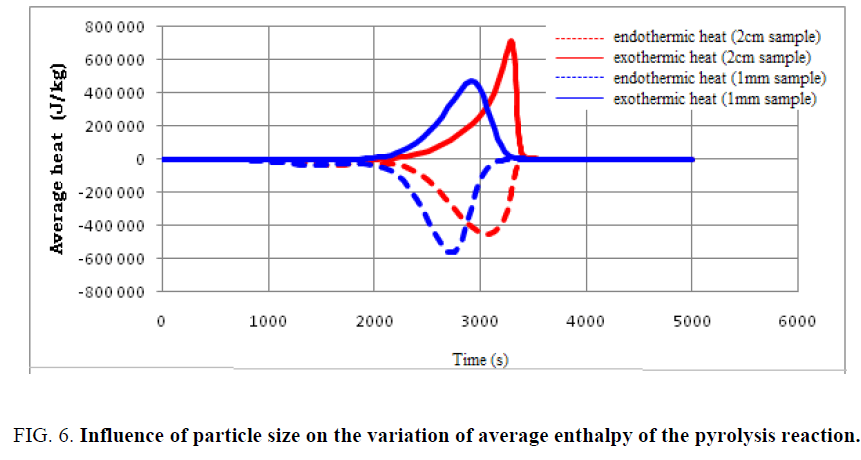
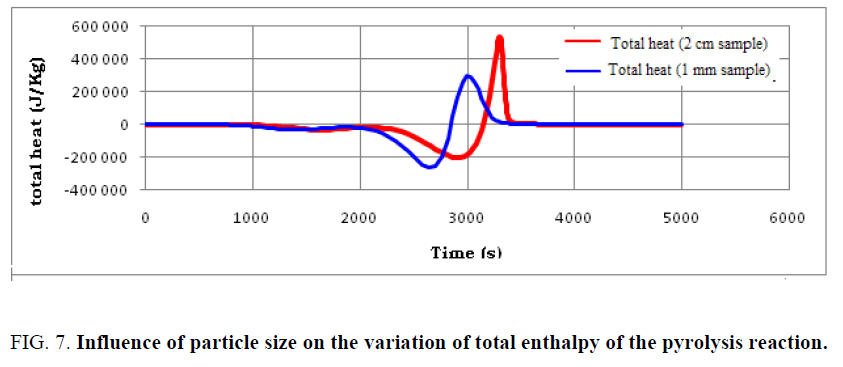
The particle size of the used tires is considered an important factor in determining the intensity of the overall energy used as well as the completion time of the pyrolysis reaction. In order to follow the effect of particle size on the heat distribution at the particle level, the variation of average and total enthalpies during the pyrolysis of used tires is shown in FIG. 6 and 7.
Findings can be made:
• The same aspect of heat distribution is observed for both samples; however, the evolution of the enthalpies with sample of dimension 1 mm is more advanced.
• Small particles are capable of completing the pyrolysis process in a shorter time, but the total energy requirement is higher compared to larger particles.
• Particle size is one of the operating parameters that can largely influence the amount of heat required to complete the pyrolysis.
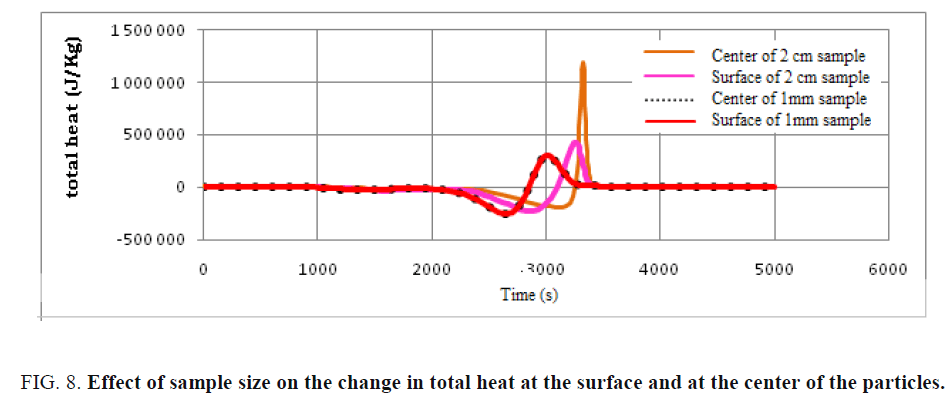
The variation of endothermic and exothermic heat at the surface of the particle and at its center was simulated and presented in FIG. 8. Note that there is a notable difference in the heat distribution between the center and the surface for the particle of dimension 2 cm, which is not the case with the particle of dimension 1 mm, this is due to the small size of the particle thus low heat transfer. The exothermic heat at the center of the particle of dimension 2 cm exceeds 1500 kJ/Kg which presents an economic and energetic payoff for the plant. Thus, by increasing the particle size, the thermal transfer between surface and center influences the overall energy rate of the pyrolysis process of used tires. It can also be observed that an increase in particle size can then increase the heat gradient.
FIG. 8: Effect of sample size on the change in total heat at the surface and at the center of the particles.
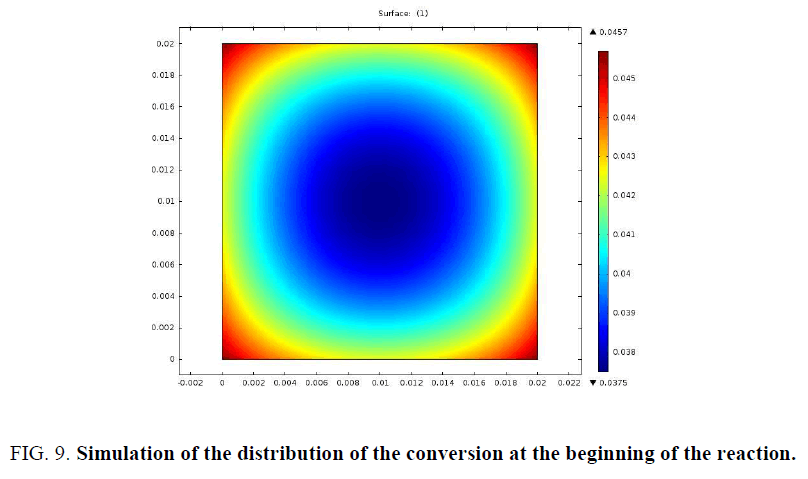
In order to better examine the distribution of mass loss and temperature at the beginning of the pyrolysis reaction, a simulation of a 2 cm sample was presented in FIG. 9 and 10.
The particle begins to consume from the edges towards the center. The profiles of the distribution of the conversion and that of the temperature at the beginning of the pyrolysis confirm this.
Conclusion
A review of the literature on the modeling of the pyrolysis process of used tires shows that these studies can be classified according to the type of reaction scheme chosen, namely single-step or multi-step reaction mechanisms. Most of these studies admit that the pyrolysis reaction is endothermic and does not take into account exothermic reactions. It is also noted that the thermal balances considered did not integrate the energy contribution of the exothermic reactions. Therefore, the model developed in this work has been designed to represent the loss of mass and heat profiles taking into account thermal phenomena and the kinetics of exothermic reactions.
After making certain assumptions about the model, the thermal balances and kinetics of each reaction were written. The resolution of the differential equations by the software makes it possible to present the profile of the variation of heat within the sample as a function of time. The conversion of the reaction was also modeled and compared with that obtained experimentally. There is a satisfactory agreement between the theoretical and the experimental results.
This work showed that the modeling of the mass loss profile and heat of the pyrolysis reaction was feasible based on the energy behavior of each reaction. It has been shown in particular that certain exothermic reactions occur during the pyrolysis of used tires. It has also been noted that the small particle size can result in faster heat transfer during pyrolysis and will shorten the process completion time, but on the other hand rapid heat transfer can also trigger more endothermic reactions that increase the overall energy consumption of the reaction.
References
- Aguado R, Olazar M, Velez D, et al. Kinetics of scrap tire pyrolysis under fast heating conditions. J Anal App Pyrol. 2005;73:290-8.
- Lin JP, Chang CY, Wu CH. Pyrolytic treatment of rubber waste: Pyrolysis kinetics of styrene-butadiene rubber. J Chem Technol Biotechnol. 1996;66(1):7-14.
- Leung DY, Wang CL. Kinetic study of scrap tire pyrolysis and combustion. J Anal App Pyrol. 1998;45(2):153-69.
- Leung DY, Wang CL. Kinetic modeling of scrap tire pyrolysis. Energy & Fuels. 1999;13(2):421-7.
- Yang J, Kaliaguine S, Roy C. Improved quantitative determination of elastomers in tire rubber by kinetic simulation of DTG curves. Rubber Chem Technol. 1993;66(2):213-29.
- Aylon E, Callen MS, Lopez JM, et al. Assessment of tire devolatilization kinetics. J Anal App Pyrol. 2005;74(1):259-64.
- Bouvier JM, Charbel F, Gelus M. Gas-solid pyrolysis of tire wastes: Kinetics and material balances of batch pyrolysis of used tires. Resources and Conservation. 1987;15(3):205-14.
- Conesa JA, Font R, Fullana A, et al. Kinetic model for the combustion of tyre wastes. Fuel. 1998;77(13):1469-75.
- Kim S, Park JK, Chun HD. Pyrolysis kinetics of scrap tire rubbers. I: Using DTG and TGA. Journal of Environmental Engineering. 1995;121(7):507-14.
- Ko DC, Mui EL, Lau KS, et al. Production of activated carbons from waste tire: Process design and economic analysis. Waste Management. 2004;24(9):875-88.
- Mui EL, Ko DC, McKay G. Production of active carbons from waste tires: A review. Carbon. 2004;42(14):2789-805.
- Seidelt S, Muller-Hagedorn M, Bockhorn H. Description of tire pyrolysis by thermal degradation behaviour of main components. Journal of Analytical and Applied Pyrolysis. 2006;75(1):11-8.
- Williams PT, Besler S. Pyrolysis-thermogravimetric analysis of tires and tire components. Fuel. 1995;74(9):1277-83.
- Lah B, Klinar D, Likozar B. Pyrolysis of natural, butadiene, styrene-butadiene rubber and tyre components: Modelling kinetics and transport phenomena at different heating rates and formulations. Chem Eng Sci. 2013;87:1-3.
- Lopez G, Aguado R, Olazar M, et al. Kinetics of scrap tire pyrolysis under vacuum conditions. Waste Mangement. 2009;29(10):2649-55.
- Quek A, Balasubramanian R. Mathematical modeling of rubber tire pyrolysis, Journal of Analytical and Applied Pyrolysis. 2012;95:1-13.
- Berrueco C, Esperanza E, Mastral FJ, et al. Pyrolysis of waste tires in an atmospheric static-bed batch reactor: Analysis of the gases obtained. J Anal App Pyr. 2005;74(1):245-53.
- Quek A, Balasubramanian R. An algorithm for the kinetics of tire pyrolysis under different heating rates. Journal of Hazardous Materials. 2009;166(1):126-32.
- Williams PT, Besler S, Taylor DT. The pyrolysis of scrap automotive tires: The influence of temperature and heating rate on product composition. Fuel. 1990;69(12):1474-82.
- Al-Salem SM, Lettieri P, Baeyens J. Kinetics and product distribution of end of life tires (ELTs) pyrolysis: A novel approach in polyisoprene and SBR thermal cracking. J Hazard Mat. 2009;172:1690-4.
- Conesa JA, Marcilla A. Kinetic study of the thermogravimetric behavior of different rubbers. J Anal App Pyrol. 1996;37(1):95-110.
- Islam MR, Haniu H, Fardoushi J. Pyrolysis kinetics behavior of solid tire wastes available in Bangladesh. Waste Management. 2009;29(2):668-77.
- Mui EL, Lee VK, Cheung WH. Kinetic modeling of waste tire carbonization. Energy & Fuels. 2008;22(3):1650-7.
- Chen KS, Yeh RZ, Chang YR. Kinetics of thermal decomposition of styrene-butadiene rubber at low heating rates in nitrogen and oxygen. Combustion and Flame. 1997;108(4):408-18.
- Lopez FA, Centeno TA, Alguacil FJ, et al. Distillation of granulated scrap tires in a pilot plant. J Haz Mat. 2011;190(1):285-92.
- Liu ZR, Tang HY, Zheng YL. (1992). Handbook of Rubber Industry, Chemical Industry Publishing House, China. 1992.
- Sommer JG. Engineered Rubber Products-Introduction to Design, Manufacture and Testing, Hanser Publishers, Munich, Germany. 2009.
- Senneca O, Salatino P, Chirone R. A fast heating-rate thermogravimetric study of the pyrolysis of scrap tires. Fuel. 1999;78(13):1575-81.
- Golub MA, Gargiulo RJ. Thermal degradation of 1, 4?polyisoprene and 1, 4?polybutadiene. Journal of Polymer Science Part C: Polymer Letters. 1972;10(1):41-9.
- Bhowmick AK, Rampalli S, Gallagher K, et al. The degradation of guayule rubber and the effect of resin components on degradation at high temperature. J App Poly Sci. 1987;33(4):1125-39.
- Brazier DW, Schwartz NV. The effect of heating rate on the thermal degradation of polybutadiene. Journal of Applied Polymer Science. 1978;22(1):113-24.
- Atal A, Levendis YA. Comparison of the combustion behavior of pulverized waste tires and coal. Fuel. 1995;74:1570-81.
- Cheung KY, Lee KL, Lam KL, et al. Integrated kinetics and heat flow modelling to optimize waste tyre pyrolysis at different heating rates. Fuel Processing Technology. 2011;92(5):856-63.
- Yang J, Roy C. A new method for DTA measurement of enthalpy change during the pyrolysis of rubbers. Thermochimica Acta. 1996;288(1):155-68.
- Oyedun AO, Lam KL, Gebreegziabher T, et al. Optimization of multi-stage pyrolysis. App Ther Eng. 2013;61(1):123-7.
- Lam K, Lee CW, Hui CW. Multi-stage waste tyre pyrolysis: An optimization approach. Chem Eng Transac. 2010;21:853.
- Chen JH, Chen KS, Tong LY. On the pyrolysis kinetics of scrap automotive tires. J Haz Mat. 2001;84(1):43-55.
- Olazar M, Aguado R, Vélez D, et al. Kinetics of scrap tire pyrolysis in a conical spouted bed reactor. Ind Eng Chem Res. 2005;44(11):3918-24.
- Yang J, Tanguy PA, Roy C. Heat transfer, mass transfer and kinetics study of the vacuum pyrolysis of a large used tire particle. Chemical Engineering Science. 1995;50(12):1909-22.