Original Article
, Volume: 12( 1)Magneto-Elastic Properties of [Fe(etz)6](BF4)2, [Fe(ptz)6](BF4)2 and [Fe(4ditz)3](BF4)2
- *Correspondence:
- Wolfgang Linert, Institute of Applied Synthetic Chemistry, Vienna University of Technology, Getreidemarkt 9/163-AC, 1060, Vienna, Austria E-mail: wolfgang.linert@tuwien.ac.at
Received: April 03, 2017; Accepted: April 27, 2017; Published: April 29, 2017
Citation: Kriegisch M, Eder F, Kryeziu MT, et al. Magneto-Elastic Properties of [Fe(etz)6](BF4)2, [Fe(ptz)6](BF4)2 and [Fe(4ditz)3](BF4)2. Phys Chem Ind J. 2017;12(1):108.
Abstract
Large single crystals of [Fe(etz)6 ](BF4 )2 , [Fe(ptz)6 ](BF4 )2 as well as polycrystalline pellets of [Fe(4ditz)3 ](BF4 )2 were grown. Here we report first measurements of outstanding physical properties like thermal expansion and magnetostriction of these compounds. A discussion of the magnetostriction within a thermodynamic model is provided. Moreover magnetization data of some of these samples are presented.
Keywords
Iron (II) complexes; Tetrazole; Magnetic susceptibility; Thermal expansion; Magnetostriction
Introduction
In a series of transition metal complexes a change of the spin state of the central ion can be initiated by external perturbations such as temperature, light, pressure or magnetic field [1,2]. A spin transition from low-spin state to high spin state represents a population of anti-bonding orbitals so that the ligand-metal bond is weakened. This in turn leads to changes in the volume of the primitive cell, which relative length-variation often differing along the primitive axes. This has been measured especially at thermally induced spin-transition systems. The possibility of magnetic induced spin transition [2] encouraged us to investigate such systems in some detail via measuring magnetostriction. As length variations, leading to the observed volume changes are expected to depend on crystal axes, we tried investigated powder samples as well as unit crystals.
The family of Fe-complexes [Fe(X)y](BF4)2 where X = ptz, etz, and 4ditz, shows a temperature and magnetically induced high-spin low-spin transition [3-11]. This transition is thermodynamically of first order, which is highlighted by the large hysteresis these compounds show in the susceptibility versus temperature measurements. This transition manifests itself in a thermal expansion with an abrupt jump and a switch from a diamagnetic low spin (LS) to a paramagnetic high spin (HS) state and vice versa. The results of the given investigations might be valuable in preparing nano-materials or even nano-machines driving mechanical changes based on changes in the environmental magnetic field.
Experimental Procedure
Chemicals and physical characterization
Chemicals characterization: Ethylamine (>98 %), propylamine (>98%), 1,4-diaminobutane (>98%), glacial acetic acid (99.8%), sodium azide (99%), sodium hydroxide (97%), triethyl orthoformate (98%), iron (II) tetrafluoroborate hexahydrate (97%) were obtained from Sigma-Aldrich. All other chemicals were standard reagent grade and used as supplied.
Physical measurements
Elemental analyses (C, H and N) were performed on a Perkin Elmer 2400 CHN Elemental Analyzer. The characterisation of the ligand was accomplished by NMR spectroscopy: 1H and 13C spectra in deuterated CDCl3 for etz and ptz ligands and DMSO for 4ditz were measured using a Bruker 250 FS FT NMR spectrometer. Proton NMR chemical shifts are reported in ppm versus TMS. Mid-range FTIR spectra of the compounds were recorded as KBr-pellets within the range 4400 to 450 cm-1 using a Perkin–Elmer 16PC FTIR spectrometer. Pellets were obtained by pressing the powdered mixture of the samples in KBr in vacuo using a hydraulic press applying a pressure of approx. 10 000 kg/cm2 for 5 min.
The magnetic susceptibilities on the [Fe(ptz)6](BF4)2 single crystal were carried out in a S600 SQUID from Cryogenics. The measurements were performed in the temperature range 5 K - 300 K at 2 K min sweeping mode under an applied magnetic field of 0.5 T.
All thermal expansion and magnetostriction measurements were carried out by a fully compensated capacitance cell based on a tilted-plate principle [12]. This cell was mounted in a variable temperature inset in a cryostat with a 9 T coil. The thermal expansion measurements were performed by warming up with a constant heating rate of 5 mK/s, also the magnetostriction measurements were performed with increasing temperature after an initial cooling to 4.2 K.
Synthesis of the ligands and complexes
The synthesis of the ligands: 1-ethyl-1H-tetrazole (etz), 1-propyl-1H-tetrazole (ptz) and 1,4-Bis (tertazol-1-yl) butane (4ditz) ligands has been performed according to literature by Kamiya and Saito [13].
1-ethyl-1H-tetrazole (etz): 1H NMR (250.13 MHz, CDCl3-d1) δ [ppm]: 8.71 (s, 1H , Ha); 4.42 (m, J = 7.3 Hz, 2H, Hb); 1.47 (t, J = 7.3 Hz, 2H, Hc).13C NMR (62.86 MHz, CDCl3-d1) d [ppm]: 142.8 (d, Ca); 44.0 (t, Cb); 15.4 (q, Cc). IR: vC-H(tz) = 3133 cm-1.
1-propyl-1H-tetrazole (ptz): 1H NMR (250.13 MHz, CDCl3-d1) δ [ppm]: 8.67 (s, 1H , Ha); 4.38 (t, J = 7.3 Hz, 2H, Hb); 1.92 (m, J = 7.3 Hz, 2H, Hc); 0.90 (t, J = 7.3 Hz, 3H, Hd). 13C NMR (62.86 MHz, CDCl3-d1) δ [ppm]: 143.3 (d, Ca); 50.2 (t, Cb); 23.4 (t, Cc); 11.0 (q, Cd). IR: vC-H(tz)= 3132 cm-1.
1,4-Bis (tertazol-1-yl) butane (4ditz): 1H NMR (250.13 MHz, d6- DMSO) δ [ppm]: 1.81 (s, 2H, CH2-CH2), 4.50 (s, 2H, tz-CH2), 9.38 (s, tz-H5). 13C NMR (62.86 MHz, d6- DMSO) δ [ppm]: 26.4 (s, tz-CH - 62 CH2), 47.1(s, tz-CH2), 143.6 (s, tz-C5). IR: vC-H(tz) = 3117 cm-1.
Synthesis of [Fe(etz)6](BF4)2 has also been carried out according to previous published papers [3-6]. Sin-gle crystals of the complex were produced following a method described in Spin?Crossover System, Part-1 [4] with some modifications. 1.224 mmol of ethyltetrazole and 0.204 mmol of Fe(BF4)2 ? 6 H2O and a small amount of ascorbic acid (to avoid oxidation of iron (II)) were dissolved in ethanol. The iron solution was slowly added to the dissolved ligand. Single crystals (formed as hexagonal plates) were obtained after few days by a slow evaporation of the solvent. Elemental analysis for C18H36N24FeB2F8 (%): Calcd.: C 26.4; H 4.4; N 41.1. Found: C 26.3; H 3.8; N 40.7. IR: vC-H(tz) = 3168 cm-1.
Synthesis of [Fe(4ditz)3](BF4)2 has been carried out according to a procedure described in structure and physical properties of [μ-Tris (1, 4-bis (tetrazol-1-yl) butane-N4,N4‘) iron (II)] Bis (hexafluorophosphate), a New Fe (II) spin-crossover compound with a three-dimensional threefold interlocked crystal lattice. [7]. Elemental analysis for C18H30N24FeB2F8 (%): Calcd.: C 26.62; H 3.72; N 41.40. Found: C 26.20; H 3.75; N 40.40. IR: vC-H(tz) = 3148 cm-1.
All attempts of growing single crystals, big enough for our measurements, were without success for this compound. Therefore the powder of the pure complex was pressed to round pellets (r~1.5mm) with the lowest possible pressure (250 kg/cm²) in order to prevent a mechanical destruction of the samples.
Their crystal structure and spin-crossover (SCO) behavior has already been characterized in various papers [3-6,8] in more detail by using different methods such as Single-Crystal, X-ray Diffraction, Mössbauer spectroscopy, magnetic susceptibility, UV-VIS-NIR Spectroscopy, IR spectroscopy as well as Irradiation Experiments.
Synthesis of [Fe(ptz)6](BF4)2 has been previously reported in comparative investigations on a series of [hexakis (1-(tetrazol-1-yl) alkane-N4) iron (II)] bis (tetrafluoroborate) spin crossover complexes: Methyl-to butyl-substituted species [6]. Single crystals were produced according to reference [10]. Well-shaped crystals were grown from a saturated solution in nitro methane by evaporation of the solvent. The solubility was increased by slightly heating the solvent. The crystals are formed as hexagonal shaped plates with 1 cm to 2 cm diameter and a thickness of several millimeters with a layered structure. These hexagonal shaped layers are oriented perpendicular to the crystallographic c-axis. The crystal structure of this compound has been reported previously [10,11]. Elemental analysis found (calc.) for C24H48N24FeB2F8 (%): Calcd.: C 32.0; H 5.4; N 37.3. Found: C 32.2; H 5.6; N 37.1. IR: vC-H(tz) = 3136 cm-1.
Results and Discussion
Table 1, summarizes the physical properties of the three compounds according to our measurements and to literature. It is important to note that this sample class is very sensitive to humidity and also very brittle, which makes it difficult to perform measurements on the samples.
| Variables | [Fe(etz)6](BF4)2 | [Fe(4ditz)3](BF4)2 | [Fe(ptz)6](BF4)2 | ||
|---|---|---|---|---|---|
| Pressed Powder | Pressed Powder | SC – B || c | SC– B⊥ c | Pressed Powder | |
| Empirical Formula | C18H36N24B2F8Fe | C18H30N24B2F8Fe | C24H48N24B2F8Fe | ||
| Molar Weight [G/Mol] | 818.11 | 812.13 | 902.1 | 902.1 | 902.1 |
| Density [G/Cm³] | 1.424 | 1.527 | 1.312 | 1.312 | 1.312 |
| Hs-Ls Temperature [K] | |||||
| Susceptibility Cooling | 105 | 80 | 124.4 | 122.4 | -- |
| Susceptibility Heating | 105 | 89 | 134.4 | 136.2 | -- |
| Single crystal (SC) | Single crystal (SC) | ||||
| Thermal Expansion Heating | 107 | 89.4 | 138 | -- | 133.7 |
Table 1: Physical properties of the three compounds: presently measured values and from literature [1,4,5,8].
Susceptibility
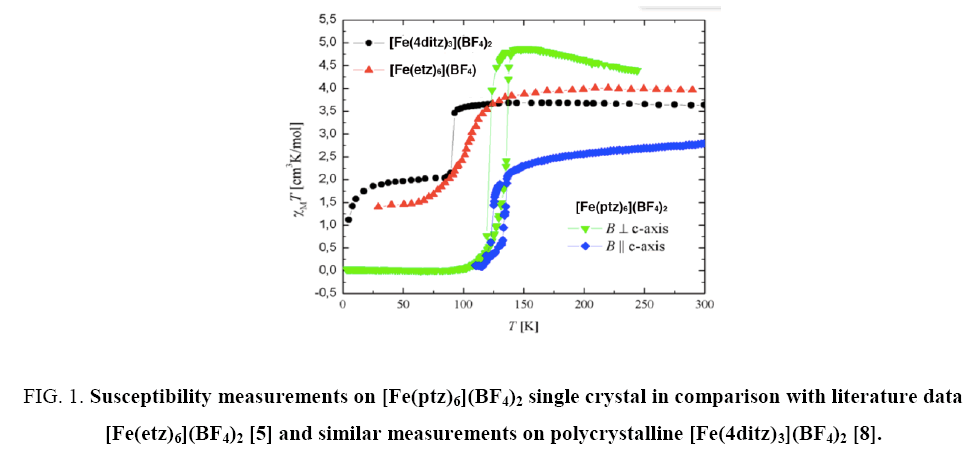
For performing the susceptibility measurements on the single crystal, the magnetic field was applied parallel and perpendicular to the c-axis as shown in Figure 1. The remarkable difference of the susceptibility for applying B parallel or perpendicular to the c-axis can be understood from the complex structure. This leads also to a magnetic anisotropic behavior. It seems that the paramagnetic moments are not randomly distributed. (The units used in Figure 1, are related to densities is given in mol/cm3 which is meaningful such complex materials and give more sense than μeff / μB values. Such values are also referred to in the text.) The susceptibility data can be described with the modified Curie-Weiss law (χ=χ0 + C/(T-Θ)) above and below the transition. χ0 is a temperature independent diamagnetic contribution, C is the Curie constant from which the effective moment is determined and Θ is the paramagnetic Curie temperature.
Figure 1: Susceptibility measurements on [Fe(ptz)6](BF4)2 single crystal in comparison with literature data [Fe(etz)6](BF4)2 [5] and similar measurements on polycrystalline [Fe(4ditz)3](BF4)2 [8].
The effective magnetic moment for B perpendicular to the c-axis is 6.49 μB per formula unit. As Θ=0.3 K, the sample shows normal Curie-like behavior. No diamagnetic corrections were applied, so χ0 shows a small negative contribution of the diamagnetic ligand. However, at low temperatures (3 K to 30 K) the effective magnetic moment is 0.5 μB / f.u., resulting in approx. 0.6% of Fe atoms remaining in high-spin state. Thus one can say that this single crystal exhibits highest purity ever obtained and reported, as 99.4% of the Fe atoms were switched from HS to LS state.
For B=μ0H parallel to the c-axis the effective magnetic moment is almost equal to 6.43 μB per formula unit. It is important to note that the Parameter Θ is approx. -142 K. This behavior (the value is quite high) can be explained by anti-ferromagnetic fluctuations (occurring in the paramagnetic range. Obviously, the transition range has not been included), which let χ shrink and give rise to a large negative value of Θ. The values of all magnetic measurements are presented in Table 2. The Jahn-Teller effect pronouncing the difference between dz2, dx2-y2 on the one hand and dxy, dxz, and dyz on the other hand, in case of the high spin state might explain the differences in the magnetic susceptibility parallel and orthogonal to the magnetic field.
| Variables | [Fe(ptz)6](BF4)2 | ||
|---|---|---|---|
| SC – B || c | SC– B⊥ c | Pressed Powder | |
| CW-Fit [150-300K] | |||
| µeff [µb] | 6.43 | 6.49 | - |
| Θ [K] | -142.6 | 0.32 | - |
| χ0 | -37.9 | -57.2 | - |
| CW-Fit [3-30K] | |||
| µeff [µb] | - | 0.5 | - |
| Θ [K] | - | -0.53 | - |
| χ0 | - | -45.2 | - |
Table 2: Susceptibility data of the Curie-Weiss fits on [Fe(ptz)6](BF4)2.
Thermal expansion and magnetostriction
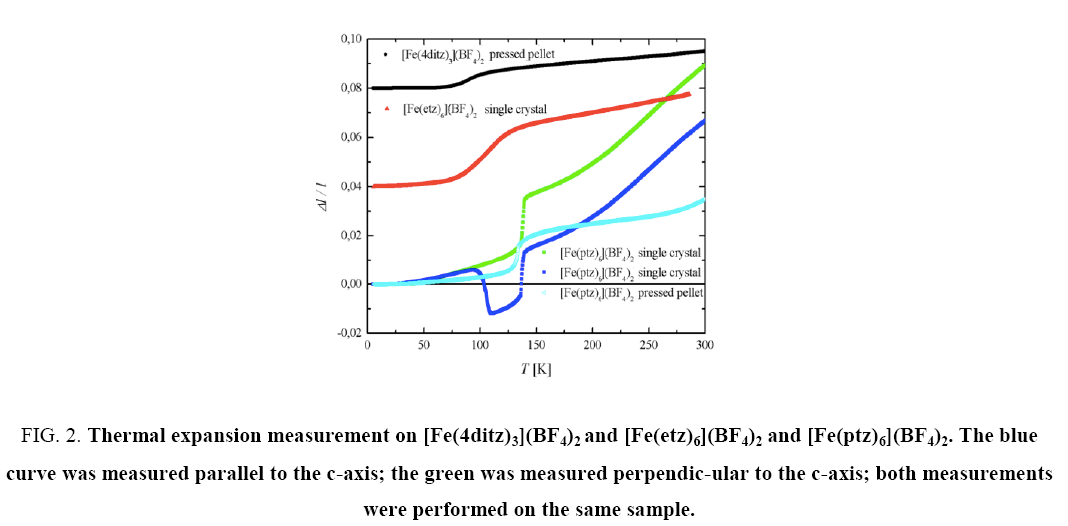
Figure 2, shows in the thermal expansion measurements a step at the HS-LS transition temperature for all three samples. A summary of the different transition temperatures is given in Table 1. Within these measurements only data during the warming up period were taken, therefore no hysteresis effects are visible.
Figure 2: Thermal expansion measurement on [Fe(4ditz)3](BF4)2 and [Fe(etz)6](BF4)2 and [Fe(ptz)6](BF4)2. The blue curve was measured parallel to the c-axis; the green was measured perpendic-ular to the c-axis; both measurements were performed on the same sample.
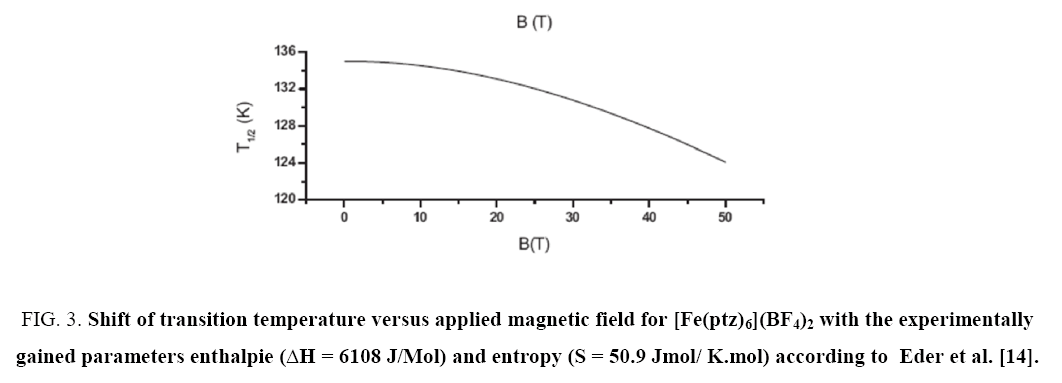
As previously reported by Edera et al. [14], the transition can be shifted to lower temperatures by applying a magnetic field. This explanation is based on a thermodynamically based model as was published [14]. In a previous paper the modelling of spin crossover systems with a special focus on molecular vibrations and on the effect of a magnetic field was discussed.
Two different theoretical models were applied, namely: a thermodynamic model and an Ising like model including molecular vibrations. A combination two already existing Ising like models – one including the effect of an external magnetic field and the other taking molecular vibrations into account - was also examined. In all calculations a field dependence of the spin crossover transition temperature T1/2 became evident.
Equation (1) gives an expression for the field dependence of the spin crossover transition temperature.
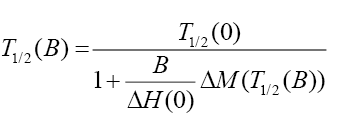 (1)
(1)
Where ΔH(0) is the enthalpy and entropy difference between LS and HS state,
ΔM(T1/2(B)) jump in magnetization at the spin transition temperature T1/2 in a field B.
According to this formula an external magnetic field induces a downward shift of T1/2 ( Figure 3).
Figure 3: Shift of transition temperature versus applied magnetic field for [Fe(ptz)6](BF4)2 with the experimentally gained parameters enthalpie (ΔH = 6108 J/Mol) and entropy (S = 50.9 Jmol/ K.mol) according to Eder et al. [14].
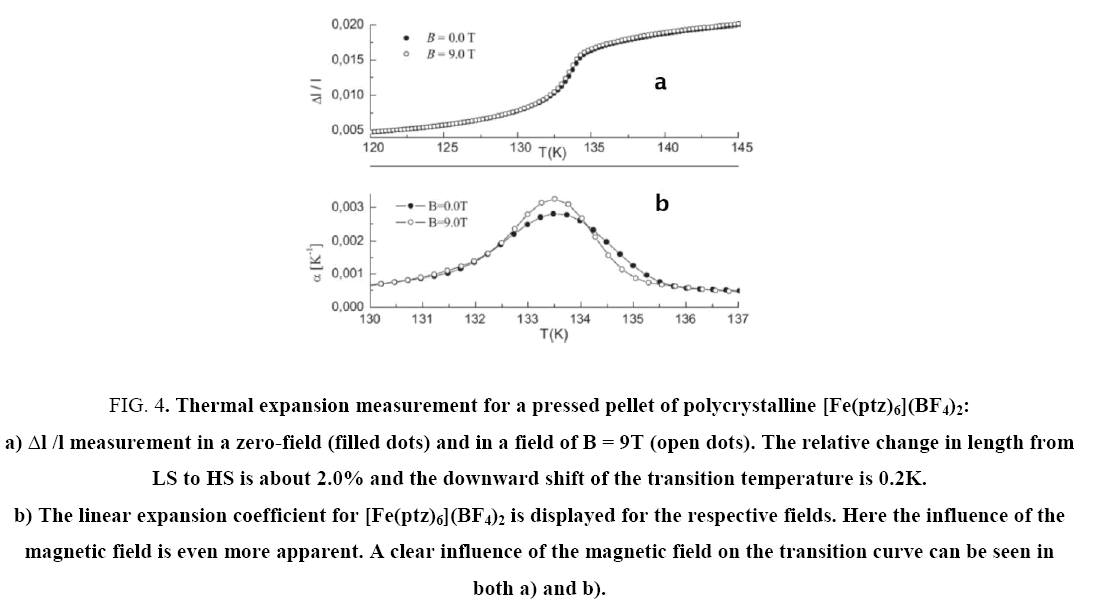
This corresponds to the results of high magnetic field experiments and thermal expansion experiments. An anomaly was observed in the [Fe(ptz)6](BF4)2 sample: a second step can occur below the spin-crossover transition (at T~100K). The origin is not fully understood, but same behavior in magnetization measurements was reported earlier in similar samples [8,15]. It seems that this effect comes from a freezing of a metasTable HS-LS state due to a very high cooling rate at the HS-LS transition. Repetitive measurements with different cooling rates were performed confirming this behavior. As all thermal expansion measurements were performed during the heating up period, one can only observe the second (= higher) HS-LS transition temperature. All three thermal expansion curves have in common that the value of length change is quite high (from 1.5 to 8%), resulting in a thermal expansion coefficient α from 10-4 K-1 to 10-3 K-1 ( Figure 4), according to Eder et al. [14].
Figure 4: Thermal expansion measurement for a pressed pellet of polycrystalline [Fe(ptz)6](BF4)2: a) Δl /l measurement in a zero-field (filled dots) and in a field of B = 9T (open dots). The relative change in length from LS to HS is about 2.0% and the downward shift of the transition temperature is 0.2K. b) The linear expansion coefficient for [Fe(ptz)6](BF4)2 is displayed for the respective fields. Here the influence of the magnetic field is even more apparent. A clear influence of the magnetic field on the transition curve can be seen in both a) and b).
This can be taken as an indication for a mechanically very soft material, which means softening of the elastic constants. Such high values for α are usually obtained for liquids which is also in agreement with this crystal structure with rather low packing factor. More over one can deduce here, that the respective ligands, acting as “spacers” between the central metal ions having different elastic properties.
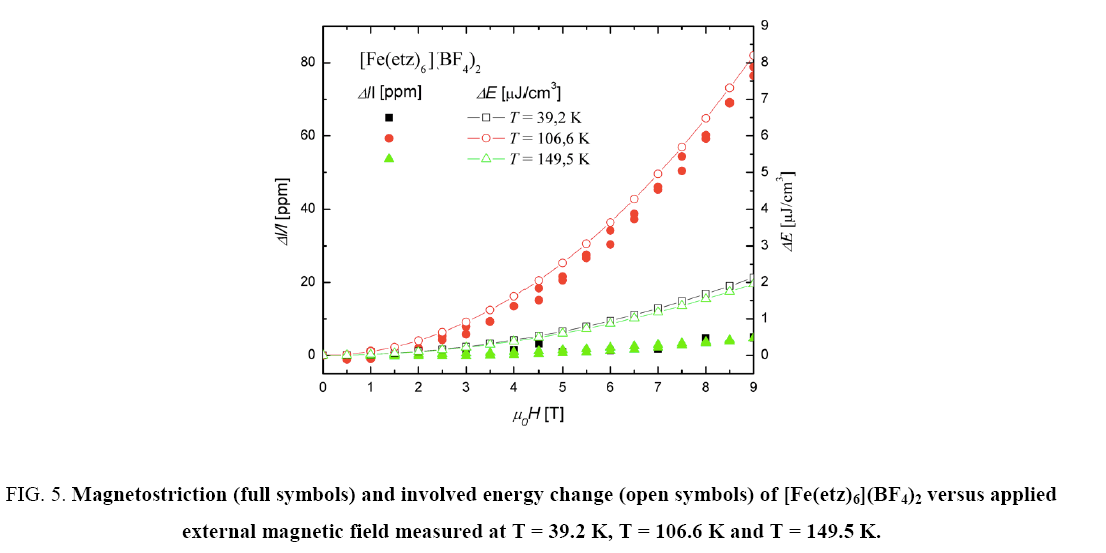
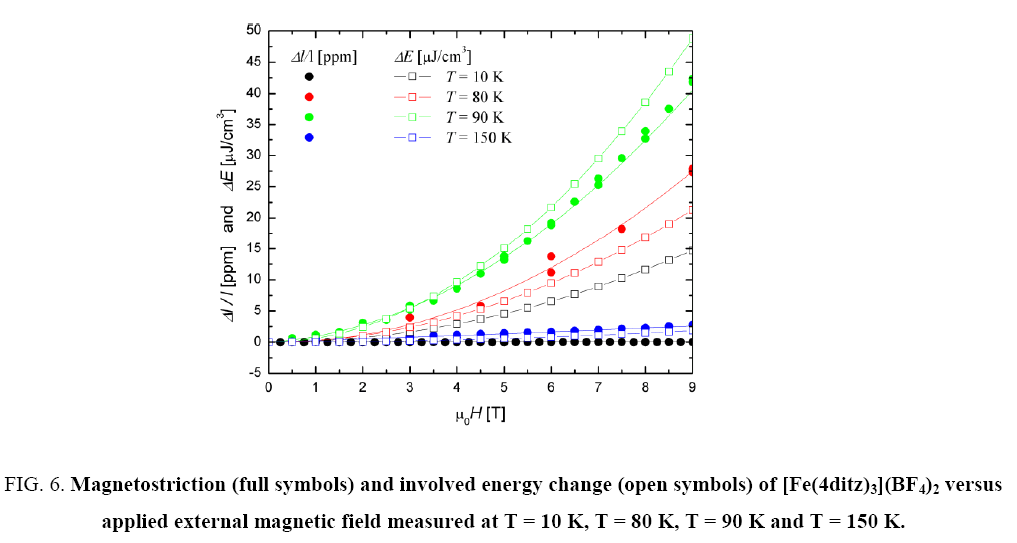
Magnetostriction denotes the change of dimensions and/or shape of a sample under the influence of a magnetic field. Only on two samples, namely [Fe(etz)6](BF4)2 and [Fe(4ditz)3](BF4)2, it was possible to measure magnetostriction. The results can be seen in Figure 5 and Figure 6.
Figure 5: Magnetostriction (full symbols) and involved energy change (open symbols) of [Fe(etz)6](BF4)2 versus applied external magnetic field measured at T = 39.2 K, T = 106.6 K and T = 149.5 K.
Figure 6: Magnetostriction (full symbols) and involved energy change (open symbols) of [Fe(4ditz)3](BF4)2 versus applied external magnetic field measured at T = 10 K, T = 80 K, T = 90 K and T = 150 K.
Since magnetostriction is normally a phenomenon of magnetically ordered materials, one would not expect very high values, because all samples are paramagnetic. In this case only a polarization effect may occur.
As mentioned in the introduction, a spin crossover is usually accompanied by a change in volume. Thus the measured magnetostriction can be seen as a consequence of a field induced switching of the spin states [2]. The fact, that the highest values are obtained at T1/2 can be explained by a field induced downward shift (or high polarization effect within the transition range) of the transition temperature [14]. Also for of ?Fe(4ditz)3](BF4)2 the field polarization effect is largest close to the transition temperature (90 K).
In order to explain this unusual behavior, we use a thermodynamical model [16]. In this model we compare the change of internal energy ΔU = TΔSm with the change of the external energy due to the change of the magnetic field: -MH + ΔE = TΔSm, where ΔE is the change of lattice energy due to the external magnetic field, M is the magnetisation, H the magnetic field, T the temperature and ΔSm is the change of the magnetic entropy.
We used our magnetization measurements and data from the literature (Table 1) in order to calculate
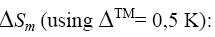
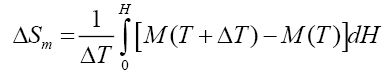 (2)
(2)
The calculated values of the field dependence agree quite good with the measurements, as can be seen in Figure 5 and Figure 6. The open symbols are the calculated values and the filled symbols are the measured ones.
When comparing the magnetostriction measurements with the calculated energy values of the field dependence, one can see that there is a good agreement. Only the T = 10 K measurement of the [Fe(4ditz)3](BF4)2 compound deviates significantly from the measurement. The reason for this deviation lies in the fact that the literature data of the magnetization shows a downturn with decreasing temperature ( Figure 1).
Generally the magnetostriction can be described with the thermodynamic model to 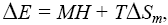 so the contribution of entropy change due to the magnetostriction is verified.
so the contribution of entropy change due to the magnetostriction is verified.
Conclusion
The magnetic and magneto elastic properties of single crystalline of [Fe(etz)6](BF4)2 and polycrystalline were investigated. The by magnetic measurements observed HS-LS transition was verified by measurements of the thermal expansion. All three thermal expansion curves show that the value of the change of length is quite high (from 1.5 to 8%), resulting in a thermal expansion coefficient varying from 10-4 K-1 to 10-3 K-1. These high values can be understood by the rather open crystal structure which corresponds a “soft material” with low values of the elastic modulus. Thermodynamic modeling shows that the transition temperature can be shifted by applying a magnetic field.
Magnetostriction measurements show a large polarization effect close to the transition temperature. The field dependence corresponds well to the change of magnetic entropy. Similar investigations on other high-spin low spin systems are proposed.
References
- Gütlich P, Goodwin HA. Spin crossover in transition metal compounds I, II, and III; Springer-Verlag: Berlin, Germany. 2004; (b) Halcrow MA (Ed.). Spin-Crossover Materials: Properties and Applications; John Wiley & Sons, Ltd. Oxford, UK. 2013.
- Richter B, Kirste A, Hansel S, et al. Field induced low-spin high-spin transition. J MagnMagn Mater. 2007;310(2):2731-3.
- Franke PL, Haasnoot JG, Zuur AP. Tetrazoles as ligands. Part IV. Iron (II) complexes of monofunctional tetrazole ligands, showing high-spin (p5T2g)? low-spin transitions. InorganicaChimicaActa. 1982;59:5-9.
- Hauser A, Gütlich P, Hinek R, et al. The [Fe (etz) 6](BF4) 2 Spin?Crossover System—Part One: High?Spin? Low?Spin Transition in Two Lattice Sites. Chemistry–A European Journal. 1996;2(11):1427-34.
- Hauser A, Hinek R, Spiering H, et al. The [Fe(etz)6](BF4)2 Spin-Crossover System—Part Two: Hysteresis in the LIESST Regime. Chemistry - A European Journal. 1996;2(11):1435-39.
- Hassan N, Weinberger P, Mereiter K, et al. Comparative investigations on a series of [hexakis (1-(tetrazol-1-yl) alkane-N4) iron (II)] bis (tetrafluoroborate) spin crossover complexes: Methyl-to butyl-substituted species. InorganicaChimicaActa. 2008;361(5):1291-7.
- Grunert CM, Schweifer J, Weinberger P, et al. Structure and physical properties of [μ-Tris (1, 4-bis (tetrazol-1-yl) butane-N4,N4‘) iron (II)] Bis (hexafluorophosphate), a New Fe (II) spin-crossover compound with a three-dimensional threefold interlocked crystal lattice. Inorganic chemistry. 2004;43(1):155-65.
- Jameson GN, Werner F, Bartel M, et al. Anion, solvent and time dependence of high?spin–low?spin interactions in a 3D coordination polymer. European Journal of Inorganic Chemistry. 2009;2009(26):3948-59.
- Jeftic J, Hinek R, Capelli SC, et al. Cooperativity in the Iron(II) spin-crossover compound [Fe(ptz)6](PF6)2under the influence of external pressure (ptz = 1-n-Propyltetrazole). Inorg Chem. 1997;36(14):3080.
- Kusz J, Guttlich P, Spiering H. Spin-crossover in transition metal compounds II. Springer Verlag, Berlin, Germany. 2004;234:129-53.
- Wiehl LE. Structures of hexakis (1-propyltetrazole) iron (II) bis (tetrafluoroborate), [Fe(CHN4C3H7)6](BF4)2, hexakis (1-methyltetrazole) iron (II) bis (tetrafluoroborate),[Fe(CHN4CH3)6](BF4)2, and the analogous perchlorates.Their relation to spin crossover behaviour and comparison of Debye–Waller factors from structure determination and Mössbauer spectroscopy. ActaCrystallographica Section B: Structural Science. 1993;49:289-303.
- Rotter M, Müller H, Gratz E, et al. A miniature capacitance dilatometer for thermal expansion and magnetostriction. Review of scientific instruments. 1998;69(7):2742-46.
- Kamiya T, Saito Y. Synthesis of 1-(2,2-Diphenylethyl)-1H-tetrazole Ger Pat. P2147023; 1973.
- Edera F, Kriegischb M, Linerta W. Mean field modeling of feii spin crossover systems in a magnetic field. Match-Communications in Mathematical and in Computer Chemistry. 2011;66(1):163-75.
- Absmeier A, Bartel M, Carbonera C, et al. Mutual influence of spacer length and noncoordinating anions on thermal and light?induced spin?crossover properties of iron (II)–α, ω?Bis (tetrazol?1?yl) alkane coordination polymers. Eur J Inorg Chem. 2007;2007(19):3047-54.
- Nizhankovskii VI. Classical magnetostriction of nickel in high magnetic field. The European Physical Journal B - Condensed Matter and Complex Systems. 2006;53(1):1-4.