Original Article
, Volume: 15( 2)Intelligent Based Controllers for Multivariable Boiler Turbine Systems
- *Correspondence:
- Deepa T, VIT University, Chennai, Tamilnadu, India, Tel: 04439931198; E-mail: deepa.t@vit.ac.in
Received: March 31, 2017; Accepted: April 18, 2017; Published: April 21, 2017
Citation: Deepa T, Lakshmi P, Balaji V. Intelligent Based Controllers for Multivariable Boiler Turbine Systems. Int J Chem Sci. 2017;15(2):122.
Abstract
The paper presents the Co-ordinated controller design of boiler turbine unit. Co-ordinated controller design is a conventional method, that controller values are optimized using the optimization techniques like Particle Swarm Optimization (PSO) and Genetic Algorithm (GA) in dynamic system. A complete analysis for each technique is presented in time domain. Performance of both controllers is examined and control performance measures for common input changes. Integral Square Error (ISE) is used as performance index for designing the controllers. Finally, a comparative assessment of each controller on the system performance is presented and discussed. From the results, it is inferred that the performance of PSO gives minimum Integral Square Error (ISE).
Keywords
Co-ordinated control; Boiler turbine units; Genetic algorithm; Particle swarm
Introduction
Multiloop single-input-single-output (SISO) controllers are often used for controlling interacting multivariable processes because of their simplicity in implementation, namely, they are easily understandable to control engineers and require fewer parameters to tune than multivariable controllers. Two multivariable systems are presented in this paper namely boiler turbine units and four tank system. Advantage of the multiloop controllers is that loop failure tolerance of the resulting control system can be easily obtained. Since some loops can be in manual mode or the manipulated variables of some loops can be saturated to their limits, the loop failure tolerance is important for practical applications [1].
The controller design for a boiler-turbine unit has attracted much attention in last two decades. Tan et al. [2] proposed a PID reduction procedure for a centralized controller and showed that the performance of the PI controller for a boiler - turbine unit did not degrade much from the original loop-shaping H∞ controller. A method for auto-tuning fully cross-coupled multivariable PID controllers from decentralized relay feedback is proposed [3]. It should be noted that modern control techniques might achieve better performance than the conventional PID controller. Zhuang et al. [4] proposed multivariable PID controllers and Shiu et al. [5] discussed sequential design method for multivariable decoupling and multiloop PID controllers.
Interaction analysis of multivariable systems has been an important issue for control structure design (such as input output pairing) and decentralized control problems. The first quantitative measure of interaction was the Relative Gain Array (RGA) introduced by Bristol [6].
A single boiler is used to generate steam that is directly fed to a single turbine. This configuration is usually called a boiler-turbine unit. The capacity of the boiler used in this configuration is very large. The control system for a power plant is usually divided into several subsystems. For example, the feed water control subsystem is used to regulate the drum level. The temperature control subsystem is used to regulate the steam temperature and the air control subsystem is used to regulate the excess oxygen. Since the coupling between the drum level, the steam temperature and the excess oxygen are not strong, then these subsystems can be designed independently. Thus, the boiler-turbine unit can be modeled as a 2 × 2 system. The two inputs are boiler firing rate (or fuel flow rate, assuming air flow rate is regulated well by air control subsystem) and governor valve position and the two outputs are electric power and throttle pressure [7].
A boiler–turbine system provides high-pressure steam to drive the turbine in thermal electric power generation. The purpose of the boiler–turbine system control is to meet the load demand of electric power while maintaining the pressure and water level in the drum within tolerance. This boiler–turbine system is usually modeled with a Multi-Input–Multi-Output (MIMO) nonlinear system [8]. Zhuang and Atherton [9] designed a diagonal PID controller tuning using an integral performance optimization procedure for a Two Input Two Output (TITO) system.
Genetic Algorithm (GA) has been demonstrated to be an appropriate tool for parameters optimization tasks and they have been used with good results. GA is a search technique used to find good solutions to optimization and search problems. They belong to a particular class of evolutionary algorithms that use techniques inspired by evolutionary biology such as inheritance, mutation, selection and crossover. A good solution is found by the GA providing a parametric fitness function to minimize [10].
Dimeo and Lee [11] discussed the application of a genetic algorithm to control system design for a boiler-turbine plant. The improved genetic algorithm for identifying multi-variables nonlinear boiler model of 300 MW power unit is introduced [12]. In this algorithm, floating-point coding, and rank - based selection, elitist reservation and grouping method are used, and the premature convergence is restrained, and the searching ability is improved.
GAs and Neural Networks are adaptive optimization method based on biological principles [13]. These problems include optimizing the weighted connections in feed-forward neural networks using both binary and real-valued representations, and using a genetic algorithm to discover novel architectures in the form of connectivity patterns for neural networks that learn using error propagation.
Application of the GA to an optimal control problem entails minimizing the Integral Squared Error (ISE) of the input and states [14]. Yuen [15] proposed by interacting with a dynamically constructed Binary Space Partitioning archive (BSP). The concept of BSP originates from the fields of computer graphics and computational geometry. The BSP archive is built up as a random tree for which its growth process reflects the evolution history of the GA, and is a quick method to query whether there is a revisit.
Subba lekshmi and Kanakaraj [16] proposed to make the system linear, non-interacting system using Genetic Algorithm. The performance/robustness comparison among the decentralized, GA and PSO controllers are designed to control the liquid level of the laboratory QTP [17].
Dongmei Zhang et al. [18] proposed an improved genetic algorithm based on simplex crossover operator is used for the parameter optimization for support vector regression to make the crossover operation obtain the gradient. To make an adjustment through linear computing in the parameters, which are beyond the constraint scope after the reflection, expansion, and compression operation on the simplex operator? To introduce the crossover validation strategy into the design of fitness function of genetic algorithm to improve the algorithm's generalization performance.
Design of frequency selective surface using Particle Swarm Optimization (PSO) technique is discussed [19,20]. The PSO algorithm is the population based optimization algorithm which can be used to solve the minimization problem [21]. Sadeghierad et al. [22] presented the optimal design of high speed axial flux generator. The GA and PSO are used for optimizing the efficiency of machine.
Bouzid Mhamdi et al. [23] proposed the algorithm that integrates the main features of GA and PSO into the optimization process to solve the complicated scattering inverse problem. Particle swarm optimization technique has been used for tuning of neural networks utilized for carrying out both forward and reverse mappings of metal inert gas (MIG) welding process [24].
El-Zonkoly [25] proposed a multi-objective index-based approach for optimally determining the size and location of multi-Distributed Generation (multi-DG) units in distribution systems with different load models. It is shown that the load models can significantly affect the optimal location and sizing of DG resources in distribution systems. The proposed function also considers a wide range of technical issues such as active and reactive power losses of the system, the voltage profile, the line loading, and the Mega Volt Ampere (MVA) intake by the grid. An optimization technique based on particle swarm optimization (PSO) is introduced.
Safdar Raza et al. [26] proposed an intelligent islanding detection technique based on artificial neural network (ANN) that employs minimal features from the power system. The accuracy of the trained ANN is improved by optimising the learning rate, momentum and number of neurons in the hidden layers using evolutionary programming (EP) and particle swarm optimisation (PSO). The performance comparison between stand-alone ANN, ANN-EP and ANN-PSO in the form of regression value is performed to obtain the best feature combination for an efficient islanding detection. The proposed technique is tested on- and off-line for various islanding and non-islanding events.
Manoj Kumar Debnath et al. [27] discussed aboutthe optimal fuzzy- PID controller tuned by hybrid differential evolution-particle swarm optimization (DEPSO) for automatic generation control of a two area multi-unit interconnected power system.
In Section II a simple model for a boiler-turbine unit on physical data are derived. Multi-loop PID control of the boiler turbine unit using PSO and GA are discussed in section III. The results and conclusions are presented in Sections IV and V respectively.
Physical Model
Simple boiler turbine model
A First-Order Plus Dead Time (FOPDT) model is often used for PID tuning for single-variable stable systems [7]. Tuning of controller for a boiler-turbine unit is important because it is helpful to find a simple model that can capture the essential dynamics, especially the coupling effect between the generated electricity and the throttle pressure.
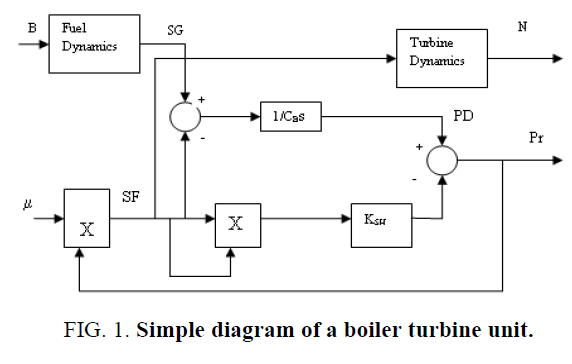
A simple diagram of a boiler turbine unit is given in Figure 1 and it shows the energy balance relation and the essential nonlinear characteristics of the boiler-turbine system.
Energy balance relation
Drum pressure PD relates the balance between the steam generation SG and the turbine steam flow SF
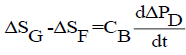 (1)
(1)
where CB- Boiler storage constant
Nonlinear characteristics
1. The pressure drop between the drum pressure PD and the steam pressure PT is related to the steam flow SF by
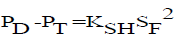 (2)
(2)
where KSH - Super heater friction drop coefficient
2. The steam flow SF is the product of the throttle pressure PT and the turbine governor position
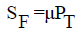 (3)
(3)
A linearized model of a boiler turbine unit [2] is
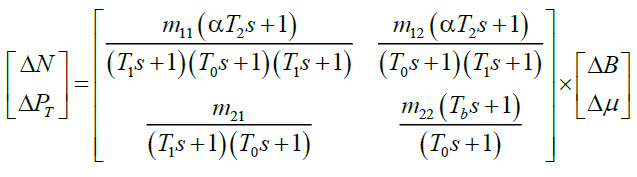 (4)
(4)
where
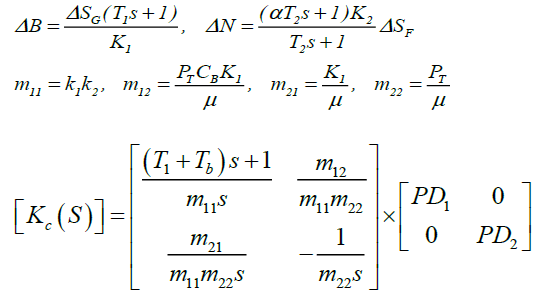 (5)
(5)
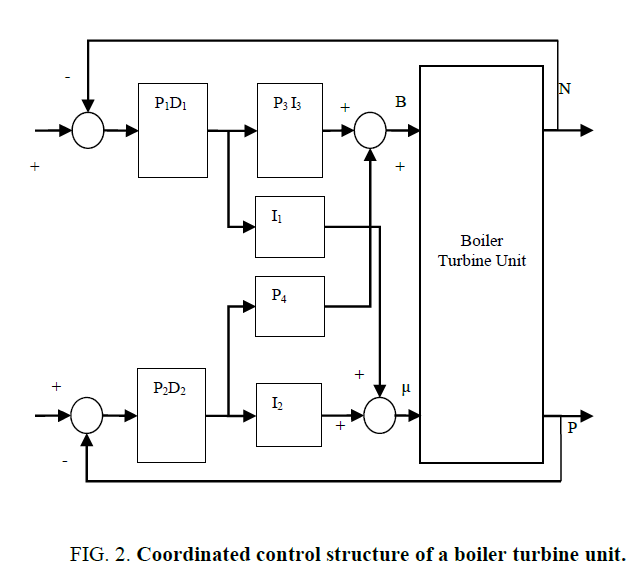
Figure 2 shows that the coordinated control structure of a boiler turbine unit [7]. The co-ordinated PID controller for the boilerturbine unit is Kc(S).
Genetic Algorithm (GA)
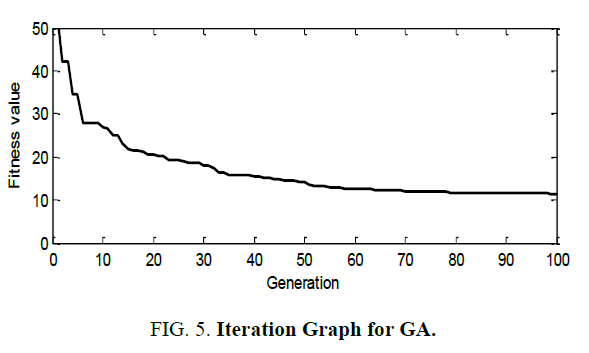
The most popular technique in evolutionary computation research has been the genetic algorithm [7]. An initial population of step response data is created. The fitness is evaluated through some appropriate measure. The algorithm is driven towards maximizing this fitness measure. For example, in a function maximization problem the fitness measure might be the function evaluation itself. Application of the GA to an optimal control problem entails minimizing the ISE of the input and states. After the fitness of the entire population has been determined, it must be determined whether or not the termination criterion has been satisfied. This criterion can be any number of things. One possibility is to stop the algorithm at some finite number of generations and designate the result as the best fit from the population. Another possibility is to test if the average fitness of the population exceeds some fraction of the best fit in the population. If the criterion is not satisfied then continue with the three genetic operators. Next, the three genetic operations of reproduction, crossover, and mutation are invoked. Fitness-proportionate reproduction is effected thought the simulated spin of a weighted roulette wheel.
The roulette wheel is biased with the fitness of each of the solution candidates. The wheel is spinned N times where N is the number of strings in the population. This operation yields a new population of strings that reflect the fitness of the previous generation's fit candidates. The next operation, crossover, is performed on two strings at a time that are selected from the population at random. Crossover involves choosing a random position in the two strings and swapping the bits that occur after this position. In one generation, the crossover operation is performed on a specified percentage of the population. This proportion of the population is specified at the initialization stage of the algorithm. The final genetic operator in the algorithm is mutation. Mutation is performed sparingly, typically every 100-1000 bit transfers from crossover, and it involves selecting a string at random as well as a bit position at random and changing it from a 1 to a 0 or vice-versa. After mutation, the new generation is complete and the procedure begins again with fitness evaluation of the population.
In a control system design using the GA the parameters that are represented as binary strings are the relevant control parameters. In the design of the Coordinated PID control system, the parameters are illustrated in Figure 2.
The GA based PI parameters are tuned using MATLAB software and these values are applied to experimental set up of four tank process. The objective function (F) considered is based on the error criterion [9]. The controller performance is evaluated in terms of ISE given by,
F=ISE (6)
where ISE=sum (1-y)2
The following GA parameters are selected for the training cycle
Population Size : 10
Selection : Roulette Wheel
Cross Over Rate : 0.8
Mutation Rate : 0.01
Generations : 100
Population Type : Double vector
Particle Swarm Optimization (PSO)
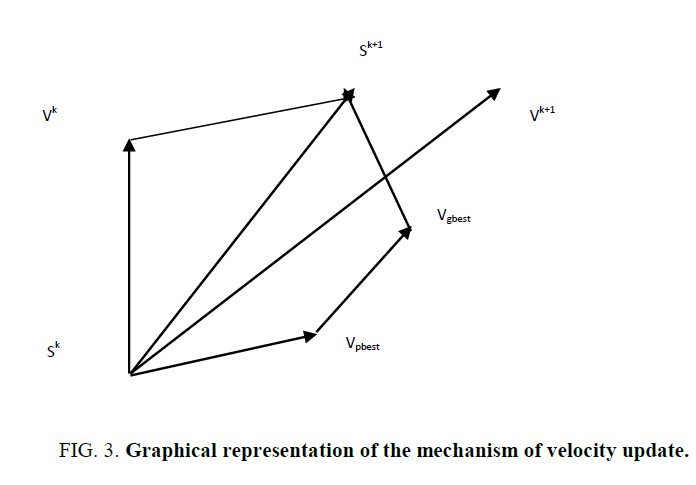
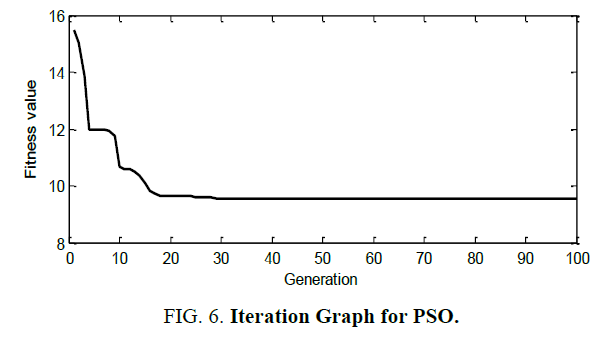
PSO is a robust stochastic optimization technique based on the movement and intelligence of swarms. PSO applies the concept of social interaction to problem solving. It was developed in 1995 by James Kennedy and Russell Eberhart. It uses a number of agents that constitute a swarm, moving around in the search space, looking for the best solution. Each particle is treated as a point in an N-dimensional space which adjusts its “flying” according to its own flying experience as well as the flying experience of other particles. Each particle keeps track of its coordinates, in the solution space, which are associated with the best solution that has achieved so far by that particle. This value is called personal best, pbest. Another best value that is tracked by the PSO is the best value obtained so far by any particle in the neighbourhood of that particle. This value is called gbest. The basic concept of PSO lies in accelerating each particle towards its pbest and the gbest locations, with a random weighted acceleration at each time step as shown in Figure 3.
where
Sk : Current searching point.
Sk+1 : Modified searching point.
Vk : Current velocity.
Vk+1 : Modified velocity.
Vpbest : Velocity based on pbest.
Vgbest : Velocity based on gbest.
Each particle tries to modify its position using various informations, such as current positions, current velocities, the distance between the current position and pbest, and the distance between the current position and the gbest. The modification of the particle’s position can be mathematically modeled according to the following equation:
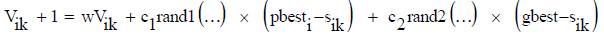 (7)
(7)
where,
Vik : velocity of agent i at iteration k,
w : weighting function,
cj : weighting factor,
rand : uniformly distributed random number between 0 and 1,
sik : current position of agent i at iteration k,
pbesti : pbest of agent i,
gbest : gbest of the group.
The following weighting function is usually utilized in the equation (7)
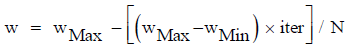 (8)
(8)
where
wMa: Initial weight,
wMin : Final weight,
N: Maximum iteration number,
iter : Current iteration number.
The new position is then determined by the sum of the previous position and the velocity
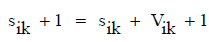 (9)
(9)
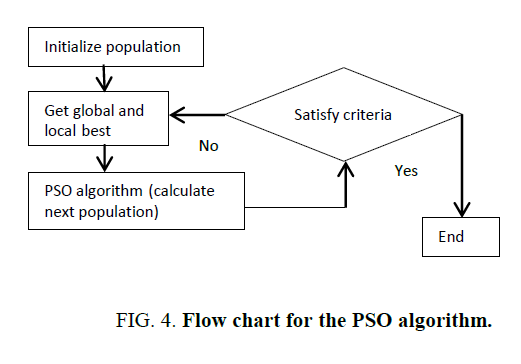
The flow chart of a general PSO algorithm [21] is developed. The optimal values of the conventional PI controller parameters Kp and Ki are found using PSO. Certain parameters of PSO need to be defined. The objective function (F) considered, is based on the error criterion (9). The controller performance is evaluated in terms of Integral Square Error (ISE) given in equation (6).
The PSO algorithm will compare the objective function evaluated at the new positions with the error criterion set by the user as illustrated in Figure 4-6. If the criterion is not satisfied, the random number generations will insure that different numerical values will be tried in the next update and the process can go on until the termination of the evaluation of the algorithm.
The following PSO parameters are selected for the training cycle for the QTP.
Size of the swarm "no of birds" (n)=50;
Maximum number of "birds steps"=100;
PSO parameter c1 =0.4;
PSO paramer c2 =0.4;
PSO momentum or inertia w =0.9;
The controller performance is evaluated in terms of Integral Square Error (ISE) and Integral Absolute Error (IAE) given by Boiler turbine unit.
ISE=ISE1+ISE2
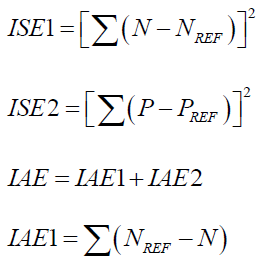
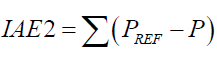 (10)
(10)
Results and Discussion
Boiler turbine unit
Example 1: Consider a boiler-turbine unit with the following transfer function which was obtained by fitting the step response data [7]:
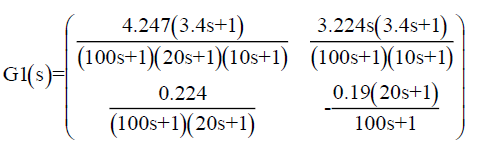
Simulations are carried out to evaluate the proposed control method by utilizing the MATLAB program. The performance of the different control strategies is compared based on the performance criteria (ISE) for the two controlled outputs electrical power and throttle pressure. The design of the disturbance is also shown for characterizing the performance of the two different control strategies.
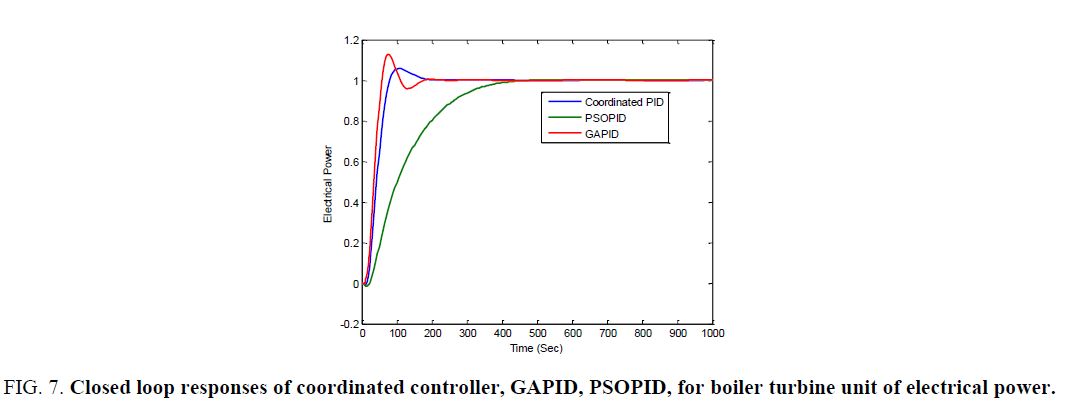
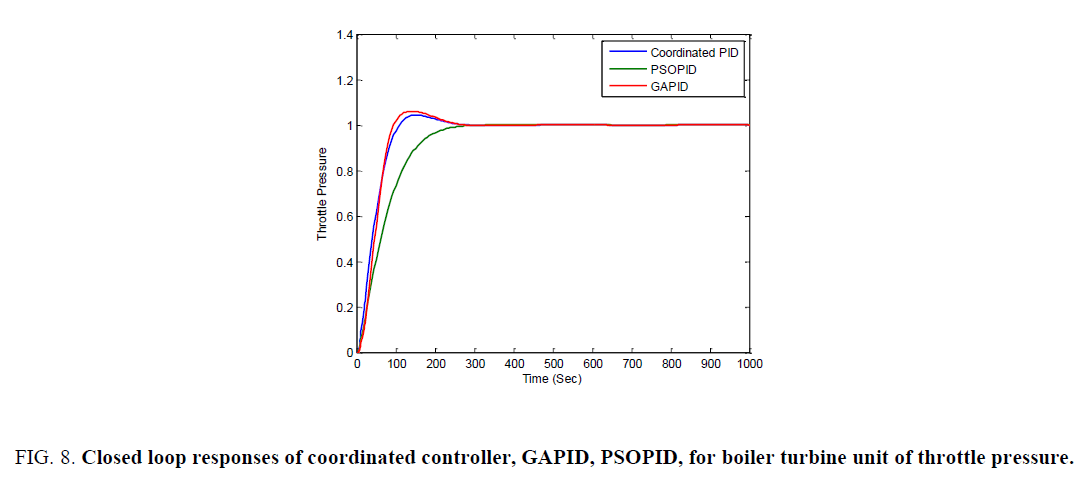
Figure 7 and 8 are the closed loop responses of the electrical power output and throttle pressure for coordinated controller GAPID and PSOPID.
Figure 7. Closed loop responses of coordinated controller, GAPID, PSOPID, for boiler turbine unit of electrical power.
Figure 8. Closed loop responses of coordinated controller, GAPID, PSOPID, for boiler turbine unit of throttle pressure.
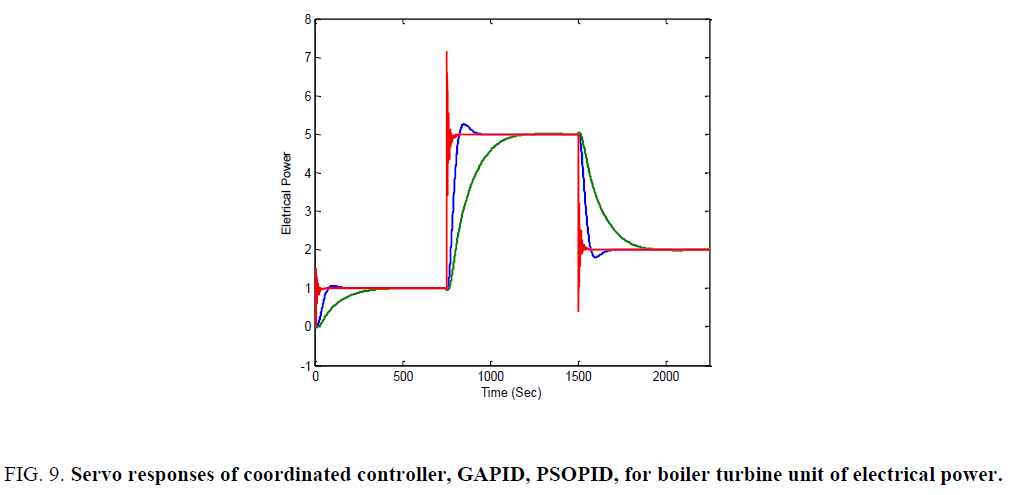
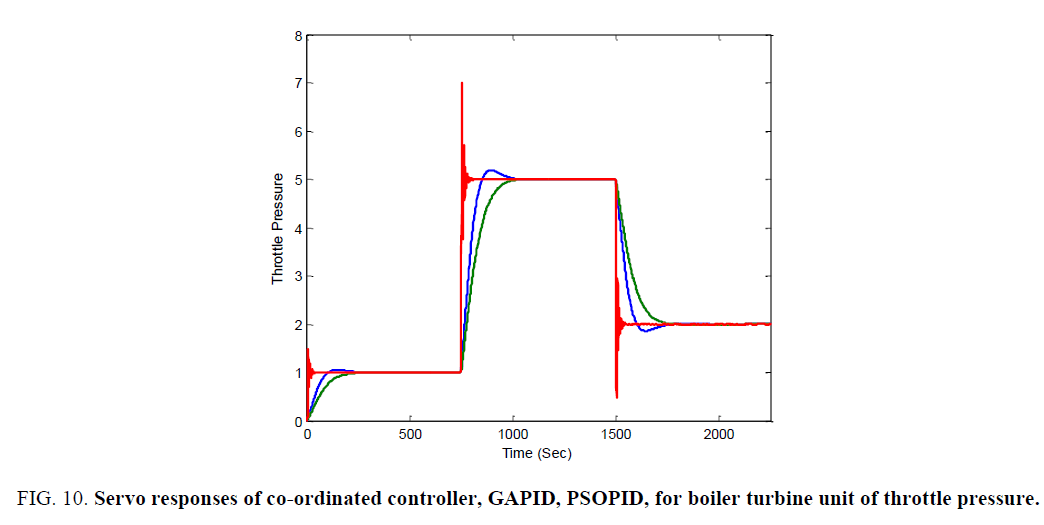
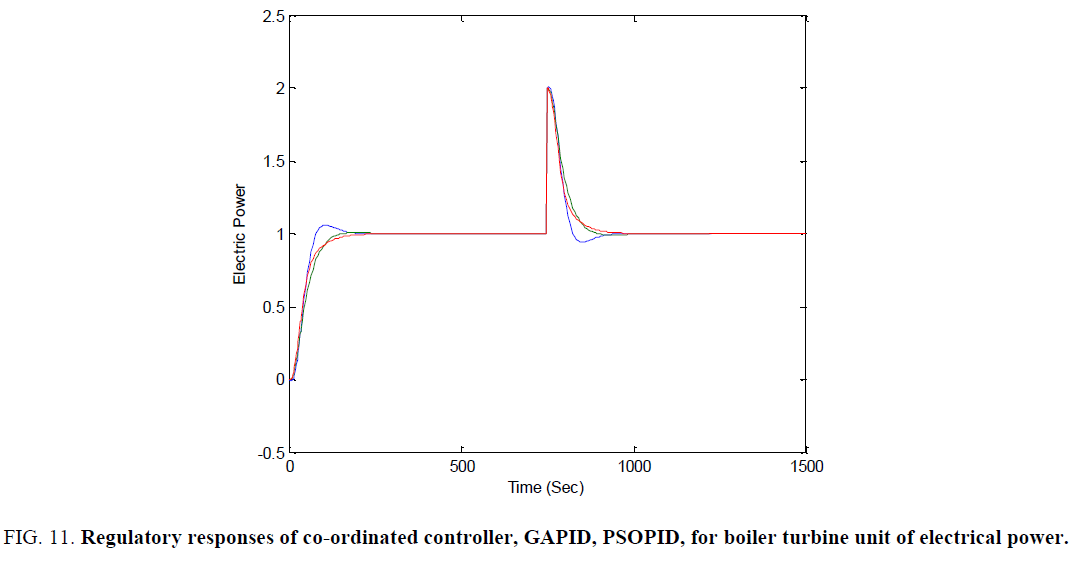
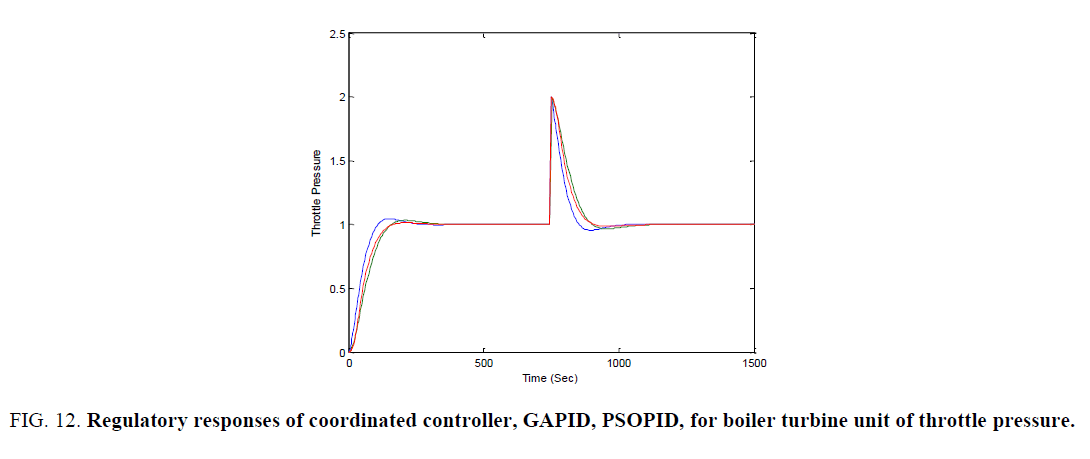
Servo responses and regulatory responses of Co-ordinated controller, GAPID, PSOPID, for Boiler turbine Unit of Electrical Power and Throttle Pressure are shown in Figure 9-12 respectively.
Figure 9. Servo responses of coordinated controller, GAPID, PSOPID, for boiler turbine unit of electrical power.
Figure 10. Servo responses of co-ordinated controller, GAPID, PSOPID, for boiler turbine unit of throttle pressure.
Figure 11. Regulatory responses of co-ordinated controller, GAPID, PSOPID, for boiler turbine unit of electrical power.
Figure 12. Regulatory responses of coordinated controller, GAPID, PSOPID, for boiler turbine unit of throttle pressure.
ISE and IAE of the controllers for both the unit step input of Electrical Power and Throttle Pressure are given in the following Table 1.
| Controllers | ISE | IAE |
|---|---|---|
| Coordinated Controllers | 0.117371 | 0.157555 |
| GAPID | 0.066894 | 0.084545 |
| PSOPID | 0.065113 | 0.080336 |
Table 1. ISE and IAE values of Coordinated controller, GAPID and PSOPID.
From the Table 1 the ISE and IAE values of PSOPID is less when compared to Coordinated controller and GAPID/. It settles quickly and the peak over shoot is less when compared to coordinated controller and GAPID.
Conclusion
The performance trade-off comparison among the coordinated controller, GAPID and PSOPID are designed to control the electric power and throttle pressure for boiler turbine units. The PSOPID responses are compared with Co-ordinated and GAPID responses. From these responses, it is observed that the ISE and IAE values are low with PSOPID than with Co-ordinated controller and GAPID. The results show that PSOPID performance is better and is effective responses.
References
- Lee J, Cho W, Edgar TF. Multiloop PI controller tuning for interacting multivariable processes. Computers and Chemical Engineering. 1998;22:1711-23.
- Tan W, Liu JZ, Tam PK. ID tuning based on loop-shaping H∞ control.IEE Proceedings on Control Theory and Applications. 1998;145:485-90.
- Wang QG, Zou Q, Lee TH, et al. Auto-tuning of multivariable PID controllers from decentralized relay feedback. Automatica. 1997;33:319-30.
- Zhuang M, Atherton DP. IEE Proceedings on control theory and applications. 1994;141:111-20.
- Shiu SJ, Huang SH. Sequential design method for multivariable decoupling and multiloop PID controllers. Industrial Engineering Chemistry Research. 1998;37:107-19.
- Bristol E. On a new measure of interaction for multivariable process control. IEEE transactions on automatic control. IEEE Trans Autom Control. 1966;11:133-4.
- Tan W, Liu J, Fang F, et al. Tuning of PID controllers for boiler-turbine units. ISA Transactions. 2004;43:571-83.
- Moon UC, Lee KY. Tuning of PID controllers for boiler-turbine units. IEEE transactions on energy conversion. 2009;24:423-30.
- Zhuang M, Atherton DP. PID controller design for a TITO system. IEE Proceedings-Control theory and applications. IEE Proceedings on Control Theory and Applications. 1994;141:111-20.
- Shopova E, Vaklievabancheva N. Basic-A genetic algorithm for engineering problems solution. Computers and Chemical Engineering. 2006;30:1293-309.
- Dimeo R, Lee KY. IEEE Transactions on Energy Conversion. 1995;10:752-9.
- Liu CL, Liu JZ, Niu YG, et al. Proceedings of the Second International Conference on Machine Learning and Cybernetics. 2003;1:314-7.
- Whitleya D, Starkweathera T, Bogarta C. Parallel computing. 1990;4:347-61.
- Goldberg DE. Addison-Wesley Publication. 1989.
- Yuen SY. IEEE Transactions on Evolutionary Computation. 2009;13:454-72.
- Subbulekshmi D, Kanakaraj J. Journal of Computer Science. 2012;8:1422-7.
- Deepa T, Lakshmi P. International Journal of Engineering and Technology. 2013;5:4660-71.
- Zhang D, Liu W, Wang A, et al. Journal of Information and Computational Science. 2011;8:911-20.
- Yang XS. Wiley. 2010.
- Genovesi S, Mittra R, Monorchio A, et al. IEEE Transactions on antennas and wireless propagation letters. 2006;5:277-9.
- Del Valle Y, Venayagamoorthy GK, Mohagheghi S, et al. IEEE Transactions on Evolutionary computations. 2008;12:171-95.
- Sadeghierad M, Darabi A, Lesani H. International Journal of Electrical Power and Energy Systems. 2010;32:804-8.
- Mhamdi B, Grayaa K, Aguili T. International Journal of Electronics and Communications. 2011;65:1032-9.
- Rakesh M, Dilip KP. Swarm and evolutionary computing. 2011;1:223-35.
- El-Zonkoly AM. Swarm and evolutionary computing. 2011;1:50-9.
- Raza S, Mokhlis H, Arof H, et al. IET Renewable power generation. 2016;10:1255-63.
- Manoj KD, Sabita T, Mallick RK. IEEE Uttar Pradesh Section International Conference on Electrical, Computer and Electronics Engineering (UPCON). 2016;pp:537-42.