Original Article
, Volume: 15( 3)Effects of Radiation and Chemical Reaction on MHD Flow Past an Oscillating Inclined Porous Plate with Variable Temperature and Mass Diffusion
- *Correspondence:
- Hari Krishna Y , Department of Mathematics, KL University, Vaddeswaram, India, Tel: 0863-239 9999; E-mail: yaraganihari@gmail.com
Received: May 10, 2017; Accepted: June 21, 2017; Published: June 26, 2017
Citation: Hari Krishna Y, Ramana Murthy MV, Bhikshu NL and Venkata Ramana G. Effects of Radiation and Chemical Reaction on MHD Flow Past an Oscillating Inclined Porous Plate with Variable Temperature and Mass Diffusion. Int J Chem Sci. 2017;15(3):149.
Abstract
The objective of present issue is to concentrate the radiation and compound response consequences for MHD flow of a viscous, incompressible and electrically directing fluid past a swaying slanted porous plate with variable divider temperature and mass dissemination within the sight of crosswise over connected uniform attractive field. The non-linear fixed partial differential conditions are illuminated by perturbation technique. The impact of a few physical parameters mixing into the issue on velocity, temperature and concentration field is communicated with the assistance of graphs.
Keywords
MHD; Inclined porous plate; Radiation; Chemical reaction; Mass diffusion
Introduction
The influence of magnetic field on viscous incompressible flow of electrically conducting, radiative reactive fluid through porous medium associated with heat and mass transfer playing a key role in different areas of science and technology. The convective hence at and mass transfer flow in porous medium find several applications in many branches of science and technology like chemical industry, cooling of nuclear reactions. MHD power generators, geothermal energy extractions processes, petroleum engineering etc., [1,2]. Ganesan et al. [3] deliberate the unruly of instable natural convection flow of viscous incompressible electrically conducting fluid past an inclined plate with variable heat and mass flux’s. Reddy et al. [4] were studied the thermo diffusion and chemical effects with immediate thermal and mass diffusion in MHD mixed convection flow by Ohmic heating. Chen [5] examined the heat and mass transfer features of MHD natural convection flow over a porous, inclined surface through variable wall temperature and concentration, pleasing into consideration the properties of Ohmic heating and viscous overindulgence. The study of Sparrow et al. [6] is associated to the convection flow nearby an inclined surface in which the combined forced and free boundary layer problem has been deliberated using the similarity method. The problem of convection flow from an isothermal plate inclined at a small angle to the horizontal was studied by Hossain [7]. Alam [8] studied the combined effect of viscous dissipation and joule heating on steady MHD free convective heat and mass transfer flow of a viscous incompressible fluid past a semi-infinite inclined radiate isothermal permeable moving surface in the presence of thermophoresis. Bhuvaneswari [9] was calculated an exact analysis of radiation convective flow heat and mass transfer over an inclined plate in a porous medium.
Uddin et al. [10] were developed closed kind of the precise answer for unsteady MHD heat and mass transfer flow on a moving inclined porous heated plate within the presence of radiation and chemical action. Pal et al. [11] were studied the perturbation analysis of unsteady magnetoelectric machine fluid mechanics convective heat and mass transfer in a very physical phenomenon slip flow past a vertical permeable plate with thermal radiation and chemical action. Hashim et al. [12] delineate in heat and mass transfer of thermophoretic MHD flow over an inclined radiate equal permeable surface within the presence of warmth source/sink. Unsteady MHD radiative and with chemicals reactive free convection flow close to a moving vertical plate in porous medium was studied by Reddy et al. [13]. Raju et al. [14] analysed on MHD convective flow through porous medium in a very horizontal channel with insulated and rubberised bottom in close the presence of viscous dissipation and joule’s heating. Ravikumar et al. [15] have studied the combined effects of heat absorption and MHD on convective Rivlin-Ericksen flow past a semi-infinite vertical porous plate.
Recently, Bhikshu et al. [16] studied the effects of MHD on peristaltic transport of 4th grade fluid through a channel kept at an angle with permeability at its walls. Chandra Shekar et al. [17] were investigated the radiation impact on MHD convective heat and mass travel through a vertical plate with chemical reaction and viscous dissolution. Bhikshu et al. [18] made an attempt to study peristaltic transport of conducting Williamson fluid in a vertical asymmetric passage with heat travel past porous medium. Rajput et al. [19] have associate with the radiation impact on unsteady MHD flow through porous medium past an oscillatory inclined plate with variable temperature and mass diffusion within the presence of Hall current driven by the higher than studies, during this manuscript an attempt is made to investigate the radiation and chemical action effects on MHD flow past a porous medium past an oscillatory inclined porous plate with varying temperature and mass diffusion.
Consider a laminar flow of an electrically conducting of incompressible fluid past a semi-infinite moving permeable plate inclined at an angle α in vertical path embedded in a uniform porous medium, which is subject to thermal and concentration buoyancy effects. The X-axis is reserved along the vertical plane and Z-axis is common to it. Thus, the Z-axis lies in the horizontal plane. The plate is kept at an angle from vertical surface. The magnetic field B0 of uniform strength is applied normal to the flow. During the motion, the direction of the magnetic field changes along with the plate in such a way that it always remains perpendicular to it. This means, the direction of magnetic field is tied with the plate. Initially it has been considered that the plate as well as the fluid is at the same temperature T∞. The species concentration in the fluid is taken as C∞. At time t>0, the plate starts oscillating in its own plane with frequency ?, and temperature of the plate is raised to Tw. The concentrationC near the plate is raised linearly with respect to time. Also, it is assumed that there exists a chemical effect of 1st order at a rate Kr which is a constant between the diffusing species and the fluid. Based on the above expectations the governing equations that describe the physical situation can be given in Cartesian frame of reference as
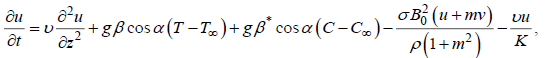 (1)
(1)
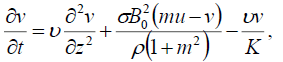 (2)
(2)
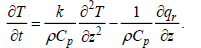 (3)
(3)
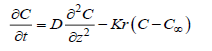 (4)
(4)
Under the boundary conditions;
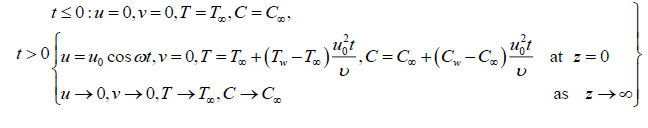 (5)
(5)
Here u is the primary velocity, v – the secondary velocity, g – the acceleration due to gravity, β – volumetric coefficient of thermal expansion, t – time, ![]() – the Hall current parameter with ωe– cyclotron frequency of electrons and τe – electron collision of time, T – temperature of the fluid β*– volumetric coefficient, C–species concentration, ν-the kinematic viscosity, ρ-the density Cp– the specific heat, k-thermal conductivity of the fluid, D – the mass diffusion coefficient, K-the permeability parameter, Tw temperature of the plate at z=0, Cw–species concentration at the plate z=0, B0– the uniform magnetic field, σ– electrical conductivity.
– the Hall current parameter with ωe– cyclotron frequency of electrons and τe – electron collision of time, T – temperature of the fluid β*– volumetric coefficient, C–species concentration, ν-the kinematic viscosity, ρ-the density Cp– the specific heat, k-thermal conductivity of the fluid, D – the mass diffusion coefficient, K-the permeability parameter, Tw temperature of the plate at z=0, Cw–species concentration at the plate z=0, B0– the uniform magnetic field, σ– electrical conductivity.
The local radiant gray gas is expressed by
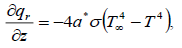 (6)
(6)
Where a* is absorption constant. The temperature difference within the flow is sufficiently small therefore, T4 can be expressed by expanding T∞ and neglecting higher-order terms
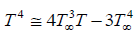 . (7)
. (7)
Using equations (6) and (7), equation (3) becomes
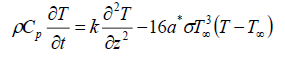 (8)
(8)
Introducing the dimensionless quantities to transform equations (1), (2), (4) and (8) into dimensionless form:
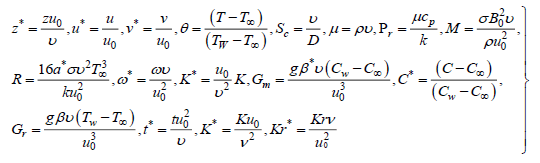 (9)
(9)
Here u,v are the dimensionless velocities, t -dimensionless, C-the dimensionless concentration, Gr–thermal Grashoff number, Gm -mass Grashof number, μ -the coefficient of viscosity, K-the dimensionless permeability parameter, Pr -the Prandtl number, Sc -the Schmidt number, R-radiation parameter, M-the magnetic parameter.
The basic field equations (1)-(4) can be expressed in the non-dimensional form and dropping the stars (*) as:
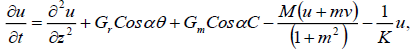 (10)
(10)
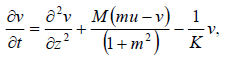 (11)
(11)
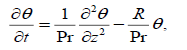 (12)
(12)
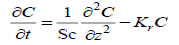 (13)
(13)
The corresponding boundary conditions are;
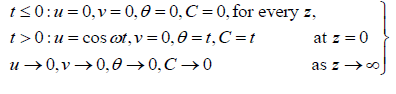 (14)
(14)
Combining equation (10) and (11), the model becomes
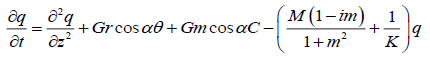 (15)
(15)
Finally, the boundary becomes:
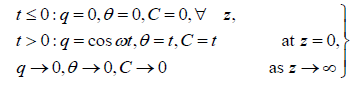 (16)
(16)
Here q = u + iv
Method of Solution
Assuming the dimensionless quantities for velocity, temperature and concentration as:
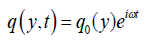 (17)
(17)
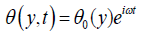 (18)
(18)
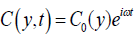 (19)
(19)
Substituting equations (17), (18) and (19) in equations (15), (12) and (13), we obtain:
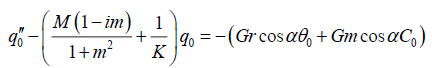 (20)
(20)
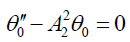 (21)
(21)
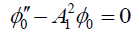 (22)
(22)
Here the summits denote the differentiation w.r.t y.
The respective boundary conditions are
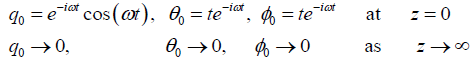 (23)
(23)
The analytical solutions of equations (20) – (22) with satisfying the equations (23) are given by
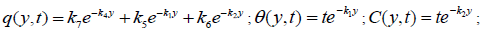
Appendix
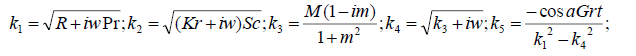
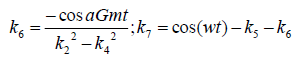
Results
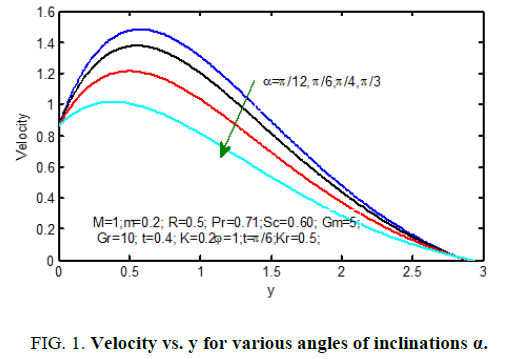
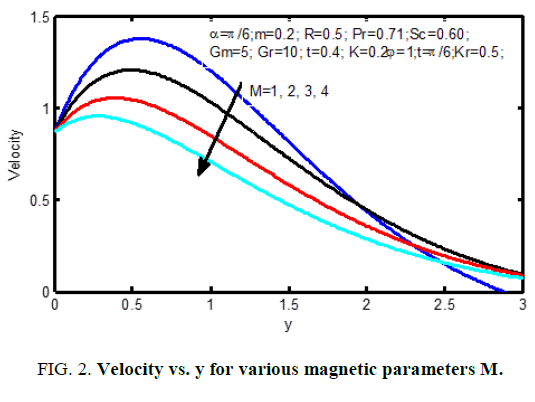
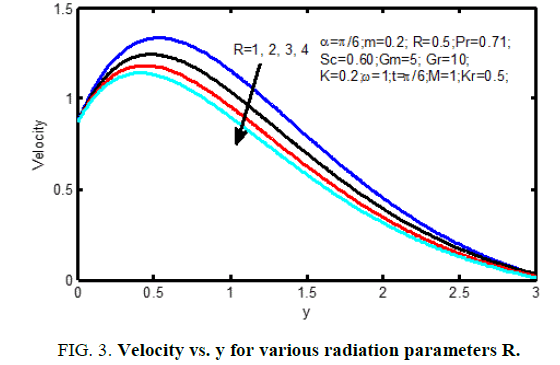
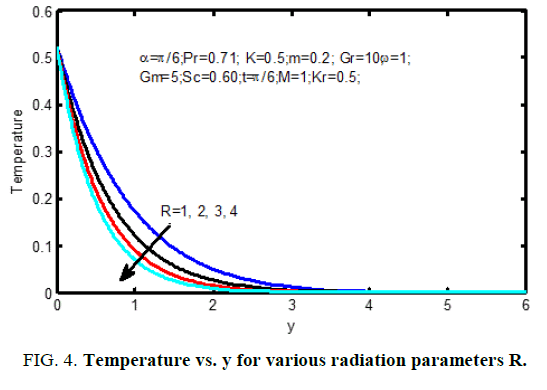
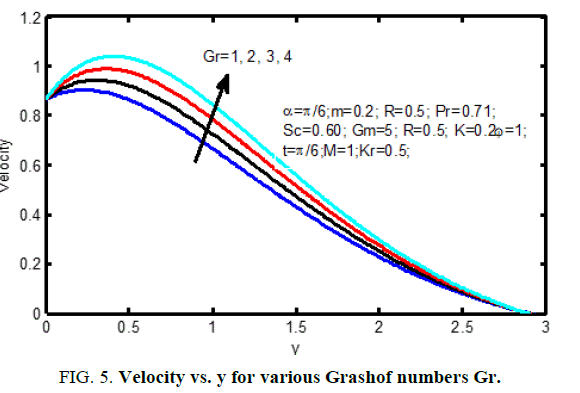
Figure. 1 displays the consequences of angle of disposition α on velocity profiles. It's pragmatic that the velocity reduces for positive change in the angle of inclination α. Figure. 2 signifies the velocity outlines for various principles of magnetic parameter M in the figure; it ascertained that the velocity decrease reduces with improvement of the magnetic parameter. the consequences of radiation parameter on velocity and temperature area unit shown in Figure. 3 and 4 respectively. It’s seen that the velocity and temperature declines with a growing the radiation parameter. The effect of thermal Grashof number on the velocity is exposed in Figure. 5.
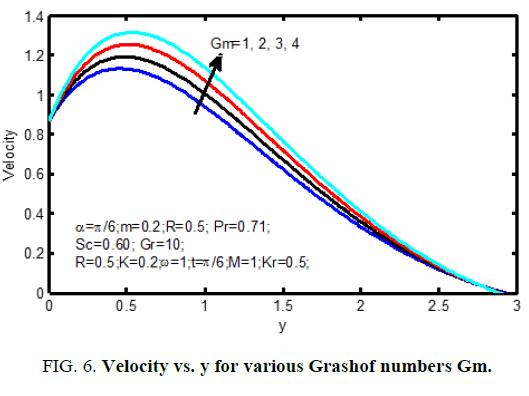
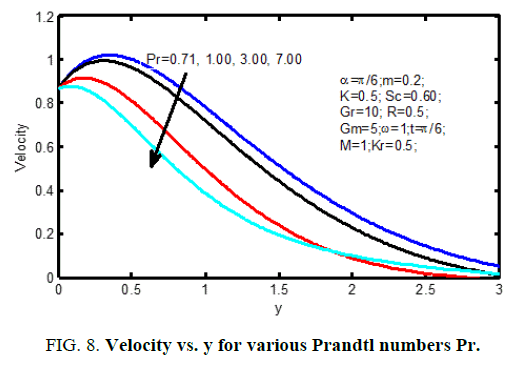
The thermal Grashof number shows the qualified result of the thermal buoyancy force to the viscous hydraulics force. The flow is quicker as a result of the event in buoyancy force matching to a growth within the thermal Grashof number. Heat is so conducted aloof from the vertical plate into the fluid that will increase the temperature and thereby enhances the buoyancy force. Additionally, it is seen that the values of the velocity improve quickly close to the plate as thermal Grashof number will increase so disintegrates swimmingly to stream velocity. Figure 6 shows velocity profiles within the physical phenomenon for different solutal Grashof number (Gm). We observe that the velocity will increase with increasing values of the solutal Grashof number. Figure. 7 shows the result of the permeability on the velocity profiles and the velocity increases with the increasing dimensionless porous parameter. Figure. 8 and 9 shows the characteristics of velocity and temperature profiles for various values Prandtl number (Pr). It is noticed that a rise within the Prandtl number results in reduction of the thermal thickness and generally lower average temperature among the physical phenomenon. the reason for that smaller values of area unit admire increase within the thermal conduction of the fluid and thus, heat will diffuse aloof from the heated surface earlier for higher values of Prandtl number (Pr).
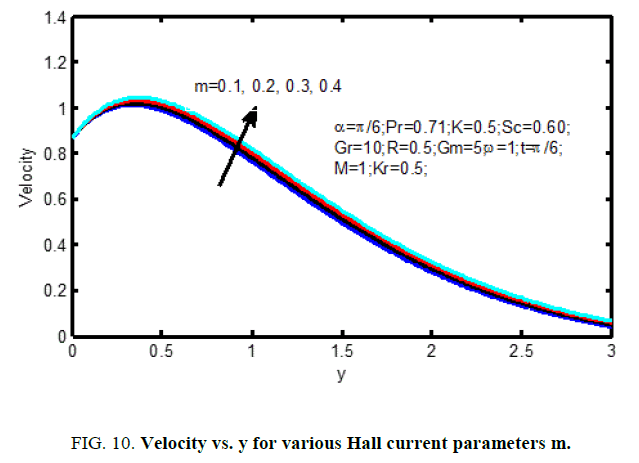
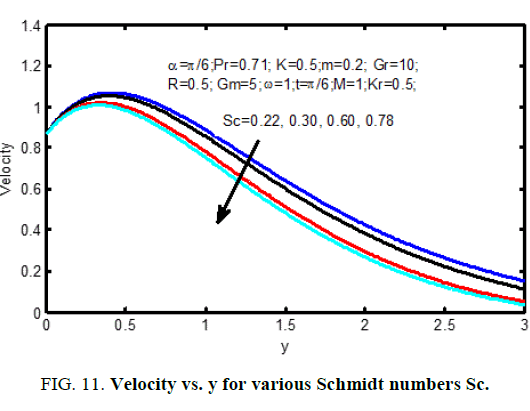
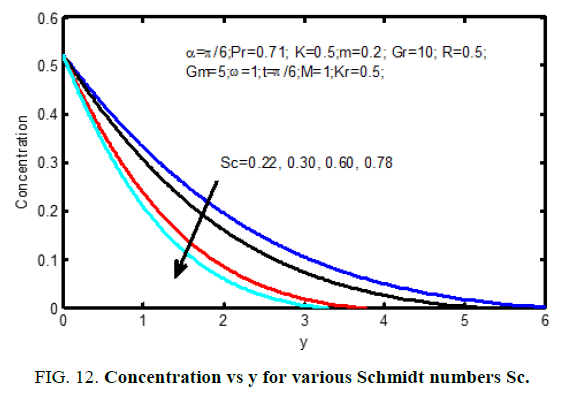
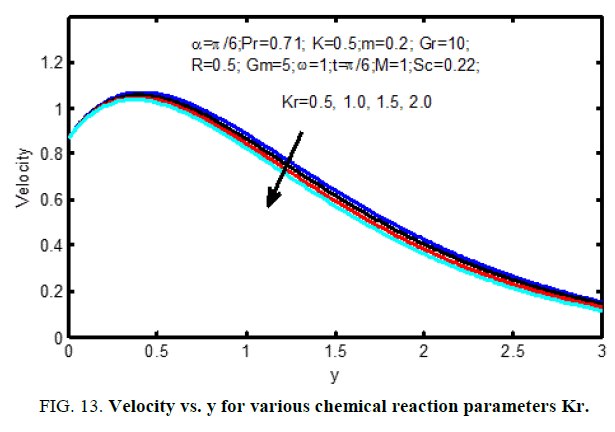
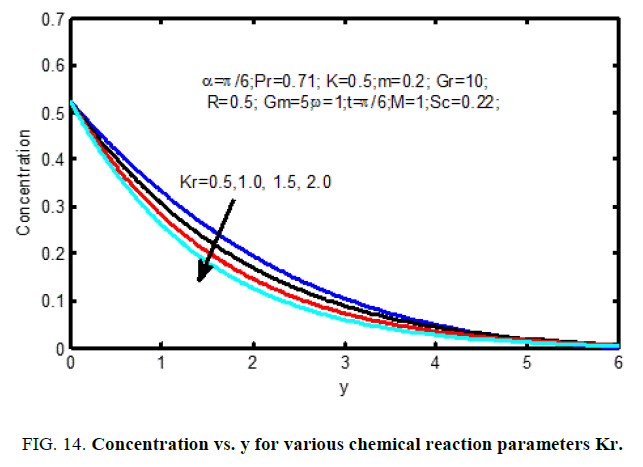
Figure. 10 shows the result of the Hall current parameter (m) on the velocity profiles. it's ascertained that for lower values Hall current parameter, the velocity will increase for increasing Hall current parameter (m). The influence of Schmidt number on the velocity profiles is shown in Figure. 11 and on concentration profiles is shown in Figure. 12. Increase in Schmidt number shows that the concentration profiles and the velocity reduce. This causes the concentration buoyancy effects to reduce yielding a reduction within the fluid velocity. Reductions within the velocity and concentration distributions area unit in the simultaneous reductions within the velocity and concentration boundary layers. Figure. 13 and 14, illustrate the behavior velocity and concentration profiles for various values of chemical action parameter (Kr). It’s ascertained that a rise in results in a decrease in each the values of velocity and concentration. a definite velocity increase happens close to the wall when that profiles decay swimmingly to the stationary price in free stream. Hence the chemical action accelerates the flow.
References
- Chaudhary RC, Sharma BK, Jha AK. Radiation effect with simultaneous thermal and mass diffusion in MHD mixed convective flow. Rom J Phys. 2006;51:715-27.
- Dulal P, Talukdar BP. Buoyancy and chemical effects on MHD mixed convection heat and mass transfer in a porous medium with thermal radiation and Ohmic heating. Common Nonlinear Sci Number Simulate. 2010;15:2878-93.
- Ganesan P, Palani G. Finite different analysis of unsteady natural convective MHD flow an inclined plate with variable surface heat and mass flux. Int J Heat Mass Transfer. 2004;47:4449-57.
- Reddy NA, Varma SVK, Raju MC. Thermo diffusion and chemical effects with simultaneous thermal and mass diffusion in MHD mixed convection flow with Ohmic heating. J Nav Archict Mar Eng. 2009;6:84-93.
- Chen CH. The heat and mass transfer characteristics of MHD natural convection flow over a permille, inclined surface with variable wall temperature and concentration. Acta Mech. 2004;172:2192-35.
- Sparrow EM, Eichhorn R, Grigg JL. Combined and free convection in a boundary layer. Physics of Fluids. 1959;2:319-20.
- Hossain MA, Pop I, Ahmed M. MHD free convection flow from an isothermal plate inclined at a small angle to the horizontal. J Theo Appl Fluid Mech. 19961:194-207
- Alam MS, Rahman MM, Sattar MA. On the effectiveness of viscous dissipation and joule heating on steady magneto hydrodynamic heat and mass transfer flow over an inclined isothermal permeable surface in the presence of thermophoresis. Commun nonlinear sci Numer simul. 2009;14:2132-43.
- Bhuvaneswari M, Sivasankaran S, Kim YJ. Exact analysis of radiation convective flow heat and mass transfer over an inclined plate in a porous medium. World Appl Sci J. 2010;10:774-8.
- Uddin Z, Kumar M. Radiation effect on unsteady MHD heat and mass transfer flow on a moving inclined porous heated plate in the presence of chemical reaction. Int J math Modell Simul Appl. 2010;3:155-63.
- Pal D, Talukdar B. Perturbation analysis of unsteady magneto hydrodynamic convective heat and mass transfer in a boundary layer slip flow past a vertical permeable plate with thermal radiation and chemical reaction. Commun nonlinear Sci Numer Simulate. 2010;15:1813-30.
- Noor NFM, Abbas Bandy S, Hashim I. Heat and mass transfer of thermophoretic MHD flow over an inclined radiate isothethermal permeable surface in the presence of heat source/sink. Int J Heat Mass Transf. 2012;55:2122-28.
- Reddy TS, Raju MC, Varma SVK. Unsteady MHD radiative and chemically reactive free convection flow near a moving vertical plate in porous medium. JAFM. 2013;6:443-51.
- Raju KVS, Reddy TS, Raj MC, et al. MHD convective flow through porous medium in a horizontal channel with insulated and impermeable bottom wall in the presence of viscous dissipation and joule?s heating. Ain Sham?s Eng J. 2014;5:543-51.
- Ravikumar V, Raju MC, Raju GSS. Combined effects of heat absorption and MHD on convective Rivlin-Ericksen flow past a semi-infinite vertical porous plate. Ain Sham?s Eng J. 2014;5:867-75.
- Bhikshu NL, Ramana Murthy MV, Ravi Kumar YVK. The effects of Magnetohydrodynamics on the peristaltic flow of fourth grade fluid in an inclined channel with permeable walls. J Chem Biol Phy Sci. 2015;5:4251-68.
- Chandra Shekar B, Naikoti K. Radiation effect on unsteady MHD convective heat and mass transfer past a vertical plate with chemical reaction and viscous dissipation. Alex Eng J. 2015;54:661-71.
- Bhikshu NL, Ramana Murthy MV, Ravi Kumar YVK. Peristaltic flow of a conducting Williamson fluid in a vertical asymmetric channel with heat transfer through porous medium. IPASJ Int J Mech Eng (IIJME). 2015;3:27-38.
- Rajput US, Kumar G. Radiation effect on unsteady MHD flow through porous medium past an oscillating inclined plate with variable temperature and mass diffusion in the presence of Hall current. Mal J Fundament App Sci. 2016;12:68-76.