Original Article
, Volume: 16( 2) DOI: 10.21767/0972-768X.1000270Effect of Methylation on 2-Hydroxypyridine in Ground State: Theoretical Study
- *Correspondence:
- Srivastava AK , Department of Physics, Indian Institute of Technology Bombay, Mumbai, India, Tel: +91-9769336195; E-mail: pushpankit@gmail.com
Received: May 08, 2018; Accepted: May 25, 2018; Published: June 02, 2018
Citation: Srivastava AK, Sinha RK, Saxena S, et al. Effect of Methylation on 2-Hydroxypyridine in Ground State: Theoretical Study. Int J Chem Sci. 2018;16(2):270
Abstract
A systematic study on the methyl substituted 2-hydroxypyridine molecule is presented in this paper to investigate the methylation effect in the ground electronic state (S0) using ab initio calculations. The minimum energy conformation of these molecules was evaluated using Hartree-Fock (HF), second order Mollar Plesset perturbation (MP2) and B3LYP density functional level of theories and TZVP Gaussian type basis set. B3LYP/TZVP level of theory was used for the natural bond orbital (NBO) calculations to get insight into the substitution energy of the stationary states and also to estimate the role of Lewis and non-Lewis (delocalization) energies. The present study reveals that stabilization of these molecules is due to the change in nuclear-electron interaction energy. However, the local interactions to methyl group are the responsible term for the delocalization energy contribution.
Keywords
2-hydroxypyridine; Ab initio; Natural Bond Orbital (NBO); Lewis energy; Delocalization energy; Structural energy; Steric energy
Introduction
Methyl group can alter enormously the pharmacological properties of a molecule and can easily change the effectiveness, nature and also the inhibition properties of the molecule. So, it is important to establish a correlation between methyl group substitution and the change in properties. For such study, methyl derivative of 2-hydroxypyridine has been taken under consideration. 2-hydroxypyridine is the tautomer of 2-pyridone which is the smallest nucleobase analogue molecule. 2-hydroxypyridine generally used as a model molecule to understand the keto-enol equilibrium in complex systems like nucleobase. In gaseous phase, 2-hydroxypyridine exhibits both the forms i.e., keto-enol. The barrier for hydroxyl to keto tautomerism is 34 kcal/mol [1]. In previous years many researchers have presented their studies on the physical properties of 2-hydroxypyridine in different ways. These two keto-enol form is one of the basic system to investigate the DNA base. Friedberg shows that this type of tautomerization causes the genetic damage through the hydrogen or proton transfer [2] which can lead to serious disease. However, repairing of the damage has also been reported earlier [3-5]. Some of the mechanisms namely nucleotide excision repair (NER), base excision repair (BER) and excitation spectrum used for the damage repairing. The tautomeric equilibrium of 2-, 3- and 4-hydroxypyridine were studied by Wang et al. in which they showed the structural changes of the molecules in presence of different solvents [6]. Sobolewski et al. studied the photo physics of the inter conversion of these two tautomeric molecules by ab initio calculations [7]. The parent molecule for our study i.e., 2- hydroxypyridine has already been studied experimentally as well theoretically.
Bernstein and co-workers reported the R2PI spectrum of the 2-hydroxypyridine and its monoclusters with water and ammonia [8]. Since the 2-hydroxypyridine and its clusters have been investigated, methylated 2-hydroxypyridines are considered to understand the effect on energies of the stationary states due to the substitution of methyl group. Methyl group substitution at different positions in 2-hydroxypyridine provides an opportunity to study the effect of methyl group on 2HP and the change in their different energies. The detailed study involves theoretical investigations which have been performed to these molecules in their ground electronic state and will be discussed in the following sections.
Results and Discussion
Ab initio optimized molecular conformations
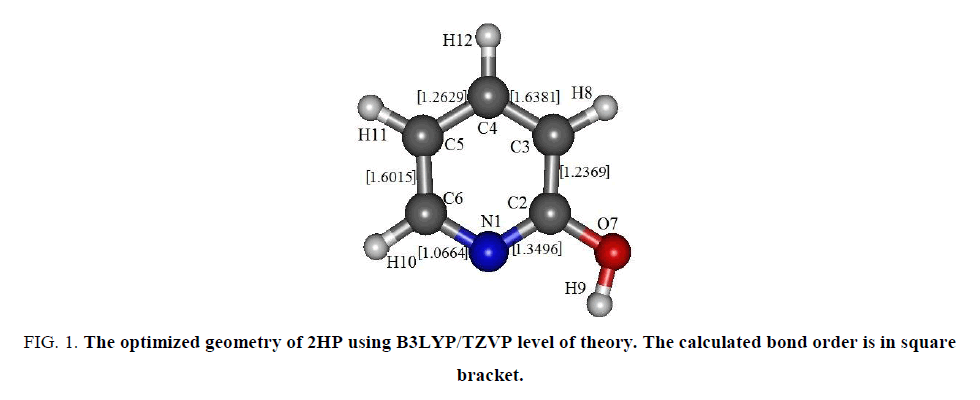
The geometry optimization of 2-hydroxypyridine in its ground electronic state (S0) were carried out using Hartree-Fock (HF), density functional theory (B3LYP) and 2nd order Moller-Plesset perturbative (MP2) levels of theory with different basis sets. For better estimation of structure and energy, the structural optimization was performed with “tight” option including ultrafine integration grid. The structural optimizations were followed by the harmonic frequency calculations to ensure that the optimized molecular structure is at the true minimum of the potential. The optimized geometry of 2-hydroxypyridine in ground electronic state using B3LYP/TZVP level of theory is shown in FIG. 1.
Figure 1: The optimized geometry of 2HP using B3LYP/TZVP level of theory. The calculated bond order is in square bracket.
During optimization of 2-hydroxypyridine using different level of theories with various basis sets, it was observed that the -OH group is eclipsed the nitrogen as reported earlier [6-8]. The localized molecular orbital (LMO) bond order calculation have also been performed to understand the double bond characteristics of the molecule and it confirms the double bond character for the bonds N1C2, C3C4 and C5C6 with higher π-bond order as mentioned in square bracket. All the calculations have been performed in Gaussian’09 package and in built NBO suit program [9]. For the visualization of the molecular geometry as well as molecular orbitals, “Gabedit-A graphical user interface for computational chemistry softwares” has been used [10]. All the other details regarding the method employed to study the molecule is provided in previous paper [11].
In the minimum energy conformation of 2-hydroxypyridine using different methods with various Gaussian basis sets, the total energy has been also calculated. The calculated total energy using different methods and basis sets is listed in TABLE 1. The total energy calculated using Hartree-Fock (HF) and 2nd order Moller-Plesset perturbative (MP2) methods is higher than that obtained from density functional theory (B3LYP). However, MP2 calculation including electron correlation predicts somewhat higher values (of the order of 321.56) for total energy compared to the obtained from HF (of the order of 321.57). The obtained results from density functional theory (B3LYP) always predict the lowest energy (of the order of 323.51) irrespective to the used basis set. Addition of polarised function along with the diffuse function in the used basis set improved the obtained result.
| Basis set/Method | B3LYP | HF | MP2 |
|---|---|---|---|
| 631G(d) | -323.515879293 | -321.567105619 | -321.563517398 |
| 631G(d,p) | -323.527585169 | -321.580835254 | -321.577730845 |
| 631+G(d,p) | -323.543695239 | -321.591055349 | -321.587674562 |
| 631++G(d,p) | -323.543801055 | -321.591179162 | -321.587804804 |
| 6311G(d,p) | -323.605637139 | -321.646907837 | -321.643530731 |
| 6311+G(d,p) | -323.613500988 | -321.652783030 | -321.649246816 |
| 6311++G(d,p) | -323.613598457 | -321.652896620 | -321.649366861 |
| TZVP | -323.633643113 | -321.672858742 | -321.669993060 |
Table 1: The calculated total energy (in Hartree) for optimized geometry using different level of theories with various basis sets.
The methyl group substitution at different positions such as ortho-, meta- and para- (with respect to nitrogen) in 2-hydroxypyridine provides an opportunity to investigate the effect of methyl group on the energy of 2-hydroxypyridine in the ground as well as in the excited electronic states (here ground state will be discussed). These four methyl substitutes of 2-hydroxypyridine having same molecular formula, are structural isomers to each other’s. The optimization of the methyl group substituted molecules was performed using different level of theories involving various basis sets. The minimum energy conformation of these molecules using B3LYP/TZVP level of theory is shown in FIG. 2. Methyl group eclipses towards the higher π bond order in the entire methylated 2-hydroxypyridine molecule.
Figure 2: The optimized geometry of (a) 3-methyl-2-hydroxypyridine (b) 4-methyl-2-hydroxypyridine (c) 5-methyl-2-hydroxypyridine (d) 6-methyl-2-hydroxypyridine in ground electronic state (S0) using B3LYP/TZVP level of theory. Corresponding calculated bond orders are in square brackets.
The geometrical parameters of 2-hydroxypyridine as well as of xM2HP (x: 3-6) in their minimum energy conformation for ground electronic state calculated using B3LYP/TZVP level of theory, are provided in the supplementary (ST1). There is no change observed for bond length O7H9 as well as no major change obtained for bond angle ∠C2O7H9 observed while methyl group substitution takes place on 2-hydroxypyridine however, little decrease observed in case of N1C2. The adjacent bond lengths such as C2C3, C4C5 and C5C6 get increased upon substitution on 3,4,5 and 6 positions of 2-hydroxypyridine respectively. To get the insight of the energy components contributing to total energy, the calculated values of total energies (TE) in their minimum energy conformation of these molecules are partitioned into the kinetic energy (KE) and potential energy (PE).
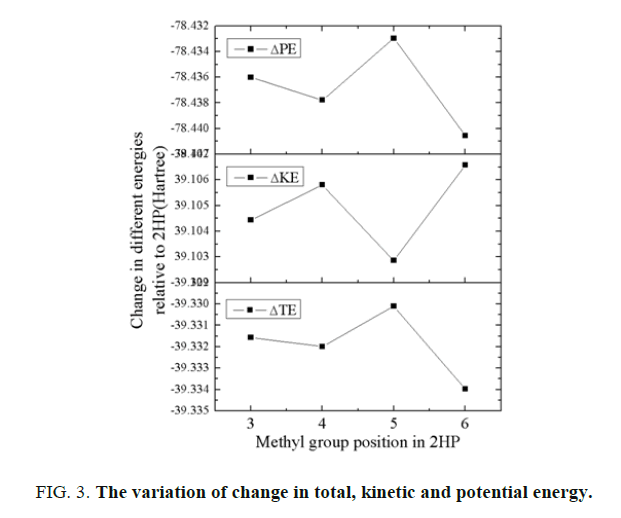
TABLE 2 shows the calculated values of total energy, kinetic energy and potential energy of these four-methyl substituents of 2-hydroxypyridine as well as of the parent molecule. It can be observed from the table; the most stabilized molecular structure belongs to 6-methyl-2-hydroxypyridine (6M2HP) among these structural isomers. Next stable molecular structure belongs to 4-methyl-2-hydroxypyridine (4M2HP) which is 5.20 kJ/mol higher than 6M2HP. 3-methyl-2-hydroxypyridine (3M2HP) and 5-methyl-2-hydroxypyridine (5M2HP) are higher in energy relative to 6M2HP by 6.31 kJ/mol and 10.15 kJ/mol respectively. The potential energy is playing an important role in the formation as well as stabilization of these substituted molecules in their ground electronic state. Current change in energies obtained for 2-hydroxypyridine while substitution, is listed in TABLE 3. The total energy can be partitioned into the kinetic and potential energy (ΔE=ΔKE + ΔPE). The kinetic energy gets increased during substitution of methyl group. Thus, the change in kinetic energy does not play important role in stabilization of the molecule. The change in potential energy (ΔPE ≈ 2ΔE) has been observed as the stabilizing factor for these molecules.
| Energy | 3M2HP | 4M2HP | 5M2HP | 6M2HP |
|---|---|---|---|---|
| ΔTE | -39.3316 | -39.3320 | -39.3301 | -39.3340 |
| ΔKE | 39.1044 | 39.1058 | 39.1028 | 39.1065 |
| ΔPE | -78.4360 | -78.4378 | -78.4330 | -78.4405 |
Table 2: . The calculated values of total energy (TE), kinetic energy (KE) and potential energy (PE) in ground state using B3LYP/TZVP level of theory. All the parameters are in Hartree. Change in TE relative to 6M2HP is in kJ/mol.
| Interaction energy | 3M2HP | 4M2HP | 5M2HP | 6M2HP |
|---|---|---|---|---|
| (ΔVnn) | 77.0312 | 72.4113 | 71.5277 | 73.5332 |
| (ΔVee) | 89.6199 | 84.9415 | 84.0684 | 86.1314 |
| (ΔVne) | -245.0871 | -235.7906 | -234.0291 | -238.1051 |
| (ΔVr) | 166.6511 | 157.3528 | 155.5962 | 159.6646 |
Table 3:Change in total energy (ΔTE), kinetic energy (ΔKE) and potential energy (ΔPE) relative to 2HP. All parameters are in Hartree.
The potential energy can be divided into the different interaction energies such as nuclear-nuclear (Vnn), electron-electron (Vee) and nuclear-electron (Vne) interaction energy. The change in contribution from these interactions is tabulated in TABLE 4.
| Bond length | In Å | Bond angle | In degree |
|---|---|---|---|
| N1C2 | -0.0030 | ∠N1C2C3 | 0.9520 |
| C2C3 | 0.0081 | ∠C2C3C4 | -1.8207 |
| C3C4 | 0.0038 | ∠C3C4C5 | 1.0836 |
| C5C6 | -0.0020 | ∠C4C5C6 | 0.1183 |
| C2O7 | 0.0038 | ∠N1C2O7 | -0.2249 |
| C4H12 | 0.0011 | - | - |
Table 4: Change in various interaction energies relative to 2-hydroxypyridine. All parameters are in Hartree.
The nuclear-electron interaction energy is the only negative term i.e. decreased which overwhelms the increase in ΔVnnand ΔVee terms. Hence from this point of view it can be said that the decrease in nuclear-electron attraction energy is the cause of the stabilization of these methylated molecules relative to 2-hydroxypyridine. The variation of change in total energy, kinetic energy and potential energy of these methylated 2-hydroxypyridine is shown in FIG. 3 relative to 2-hydroxypyridine. The change in total energy for 6-methyl-2-hydroxypyridine is minimum whereas maximum for 5M2HP. Hence 6M2HP has most stabilized structure among these structural isomers.
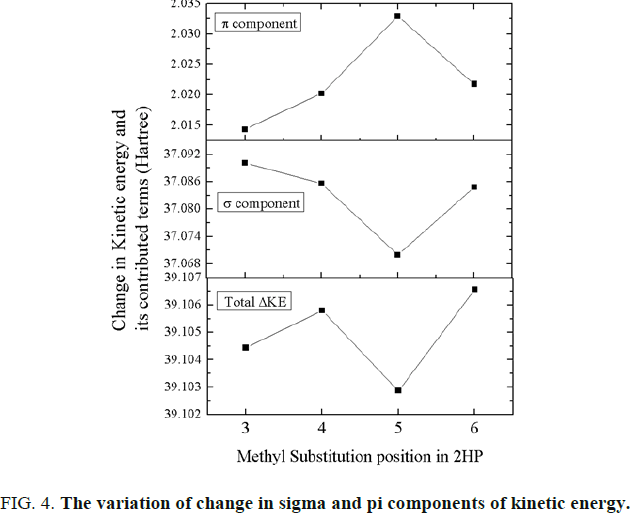
The change in kinetic energy favours 5-methyl-2-hydroxypyridine while the change in potential energy also favours 6-methyl-2-hydroxypyridine as the most stable molecular structure among these four methyl substituted 2-hydroxypyridine molecules. Hence, it can be said here that the interplay of the change in various energies play major role in stabilizing the molecular structure in their ground electronic state. The total contribution from the kinetic energy term can further be partitioned into the contribution from the σ and π components as shown in FIG. 4. Here the σ contribution is the dominant factor for the molecule to be stable. Hence the σ component overwhelms the π contributions.
Natural Bond Orbital (NBO) calculations
To get a clear picture of the contributions from the individual interactions of the molecular system, Natural Bond Orbital (NBO) analysis has been performed. In NBO analysis, the total energy of the molecule can be partitioned into the Lewis and non-Lewis energies, in determination of relative stability of the molecules. The bond order calculations were also performed using localized molecular orbital (LMO) under NBO package. NBO calculations were analyzed for all methyl substituent of 2-hydroxypyridine to find out the origin of their stability.
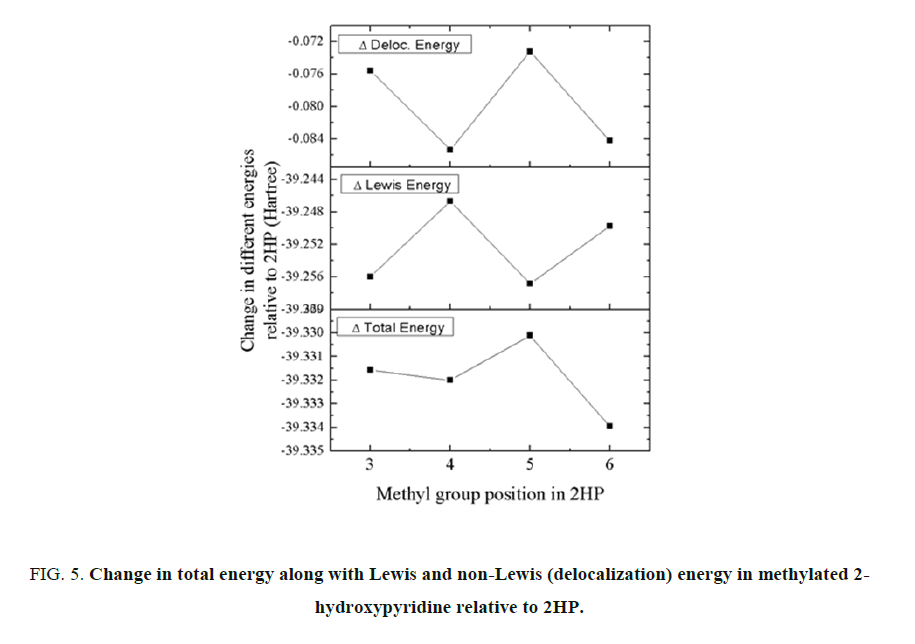
B3LYP/TZVP level of theory has been chosen for the theoretical investigation using NBO analysis. The non-Lewis (delocalization) energy is the energy obtained because of the different kind of interactions of different bonding and anti-bonding orbital and the Lewis energy is the energy due to the structural change within the molecules. The energy partitioned curve for the change in total energy of the molecules is shown in FIG. 5. In the minimum energy conformation of these methyl substituents, the most stabilized molecular structure belongs to 6-methyl-2-hydroxypyridine in all these structural isomers. The change in delocalization energy is maximum for 5-mehtyl-2-hydroxypyridine while minimum is observed for 4-methyl-2-hydroxypyridine. However, the Lewis energy change is highest for 4-methyl-2-hydroxypyridine while lowest for 5-methyl-2-hydroxypyridine. From the partition curve, it can be suggested here that, in all of these methylated 2-hydroxypyridine molecules, the delocalization energy change favours 4-methyl-2-hydroxypyridine while Lewis energy change favours the 5-methyl-2-hydroxypyridine. Hence the interplay of these two energies plays crucial role in stabilization of the molecular system in these chosen structural isomers.
In delocalization energy change, the bond-antibond and lone pair-antibond interactions has been taken into the account, however, in Lewis energy determination only the structural energy change has been used for the observation. The change in bond lengths as well as in bond angles is calculated whenever substitution of methyl group on different positions of 2-hydroxypyridine takes place. It was observed that whenever methyl group is at meta- position, major decrease observed in bond length N1C2. In the following, the detailed NBO analysis on these molecules has been discussed.
3-methyl-2-hydroxypyridine
3M2HP has one C-C single bond and one C-C double bond adjacent to methyl group. The -OH group is always inclined towards the nitrogen while the methyl group eclipsed towards the higher π bond order. The change in the geometrical parameters in minimum energy conformation is tabulated in TABLE 5. The bonds such as N1C2 and C5C6 are decreased while C2C3, C3C4, C2O7 and C4H12 get increased. There is not a major change observed in C4C5 and O7H9. The bond angles ∠C2C3C4 and ∠C3C4H12 decreases by -1.8207 and -0.7221 degrees while ∠N1C2C3 and ∠C3C4C5 get increased by 0.9520 and 1.0836 degrees respectively.
| Bond length | In Å | Bond angle | In degree |
|---|---|---|---|
| N1C2 | -0.0015 | ∠N1C2C3 | 0.2194 |
| C3C4 | 0.0034 | ∠C2C3C4 | -1.0688 |
| C4C5 | 0.0074 | ∠C3C4C5 | 1.869 |
| C5C6 | -0.0031 | ∠C4C5C6 | 1.0297 |
| C5H11 | 0.0013 | - | - |
Table 5: Change in geometrical parameters after substitution on 2HP.
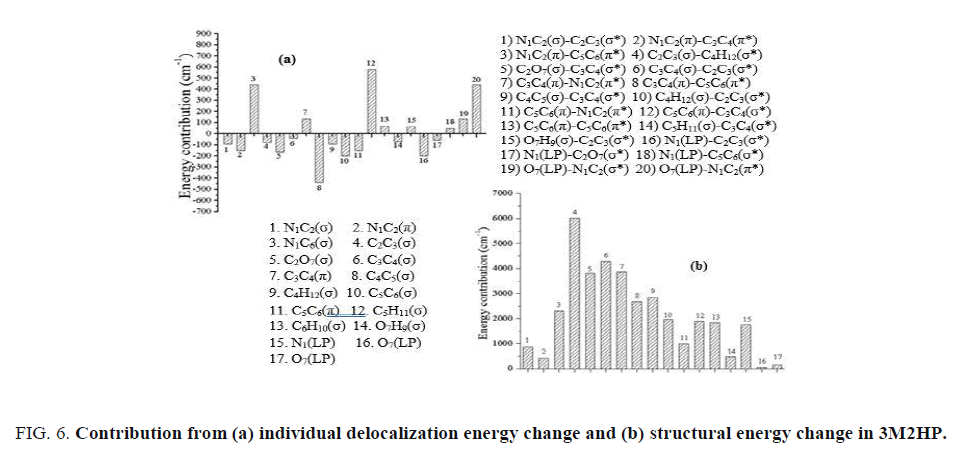
The individual delocalization energy change for 3-methyl-2-hydroxypyridine molecule is shown in FIG. 6a. In the contribution from the individual delocalization energy change, it was observed that the total contribution is positive (188 cm-1), hence does not match with the result obtained from the partitioned curve. Thus, the other interactions such as anti-bond- anti-bond, core-antibond and rydberg-anti-bond play important role in determining the total delocalization energy change. The contribution from π bond orbital of N1C2 to π anti-bond orbital of C5C6 is cancelled by the contribution from the π bond orbital of C3C4 to π anti-bond orbital of C5C6.
The overall contribution from the σ bond orbital to σ anti-bond orbital is negative. Hence, from here it can be said that the contribution from the π bond orbital to π anti-bond orbital is the dominant factor. The contribution from the change in structural energy is shown in FIG. 6b. The overall structural energy change is positive and contradicting with the result obtained from the partitioned curve. The change in Lewis energy is the sum of change in structural energy as well as of change in steric energy. Hence, the contribution from the steric energy is playing major role in determining the total Lewis energy. However, from the FIG. 6b the highest change observed as the contribution due to the maximum change in σ bond of C2C3. In structural energy change curve, the major contribution is from the σ bonds. The contribution from the π bonds is very less hence the σ bond contribution is the dominant factor.
4-methyl-2-hydroxypyridine
In this molecule, the methyl group is adjacent to one single C-C bond and one double C-C bond as observed in 3M2HP. The change in geometrical parameters while substitution took place is tabulated in TABLE 6. Due to the attachment of methyl group on C4, the adjacent bonds get affected such as C3C4 and C4C5 increased by 0.0034Å and 0.0074Å while C5C6 decreased by 0.0031Å. This change could be because of the opening of bond angles ∠C2C3C4 and ∠C4C5C6 whereas ∠C3C4C5 decreases by 1.8690 degrees. Here, the total energy of the 4-methyl-2-hydroxypyridine molecule is partitioned into contribution from delocalization and Lewis energy.
| Bond length | In Å | Bond angle | In degree |
|---|---|---|---|
| N1C2 | -0.0015 | ∠N1C2C3 | 0.2194 |
| C3C4 | 0.0034 | ∠C2C3C4 | -1.0688 |
| C4C5 | 0.0074 | ∠C3C4C5 | 1.8690 |
| C5C6 | -0.0031 | ∠C4C5C6 | 1.0297 |
| C5H11 | 0.0013 | - | - |
Table 6: Change in geometrical parameters after substitution on 2HP in 4M2HP.
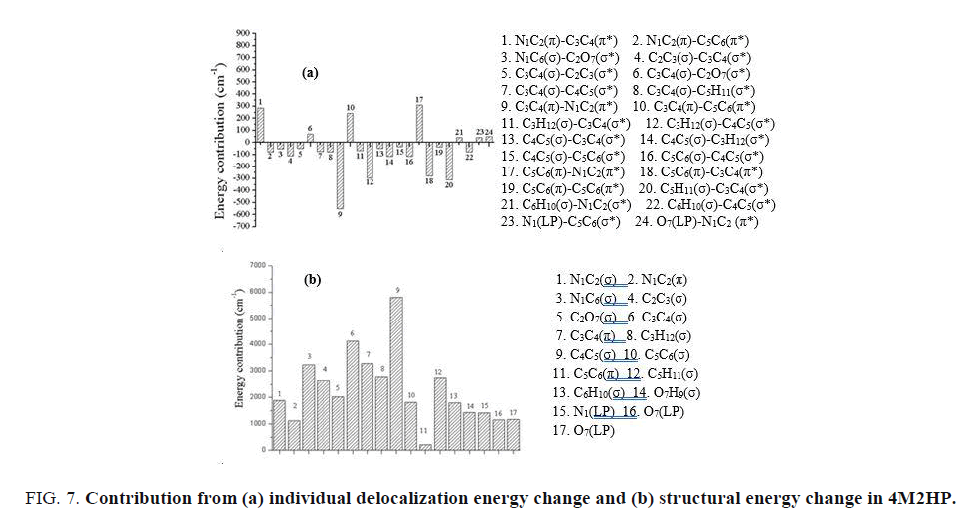
The individual delocalization energy change is shown in FIG. 7a. In this case the overall change in delocalization energy is negative (-1343cm-1). The major contribution from the interaction of π bond orbital of N1C2 and π anti-bond orbital of C3C4 is cancelled by the negative contribution from the π bond orbital of C5C6 and π anti-bond orbital of C3C4. In a similar manner the contribution from π bond orbital of C5C6 and π anti-bond orbital of N1C2 is cancelled by the σ bond orbital of C5H11 and σ anti-bond orbital of C3C4. The overall contribution from the σ bond orbital and σ anti-bond orbital is the dominant factor here in 4-methyl-2-hydroxypyridine. FIG. 7b shows the changes observed in structural energy. The overall contribution from the structural energy change is positive and does not match with the result obtained from energy partitioned curve. The change in Lewis energy can be partitioned into the change in structural energy and change in steric energy. Hence, the contribution from the steric energy is playing a major role in determining the total Lewis energy. The highest contribution is observed as σ bond of C4C5 while lowest is observed as π bond of C5C6. Since the methyl group is attached to the C4, the adjacent contribution is large. The contribution from the π bonds is very little since the σ bond contribution is the dominant factor.
5-methyl-2-hydroxypyridine
As discussed in 3M2HP and 4M2HP in a similar manner the methyl group has one single and one double C-C bond adjacent to it. The geometrical change in minimum energy conformation of 5-methyl-2-hydroxypyridine with respect to the 2-hydroxypyridine molecule is listed in TABLE 7. The bond N1C2 decreased by 0.0031Å while C4C5 and C5C6 increased by 0.0058Å and 0.0035Å respectively. The possible reason for this increase could be the closing of the bond angle ∠C4C5C6 by 1.6590 degrees. The bond angle ∠C4C3H8 decreased by 2.9220 degrees and this is because of the decrease and increase of the bond C3C4 and C4C5 respectively.
| Bond length | In Å | Bond angle | In degree |
|---|---|---|---|
| N1C2 | -0.0031 | ∠N1C2C3 | 0.1642 |
| C5C6 | 0.0054 | ∠C2C3C4 | -0.5358 |
| C2O7 | 0.0011 | ∠C3C4C5 | 0.2495 |
| - | - | ∠C4C5C6 | 0.8725 |
| - | - | ∠N1C2O7 | -0.141 |
Table 7: Change in geometrical parameters after substitution on 2HP in 5M2HP.
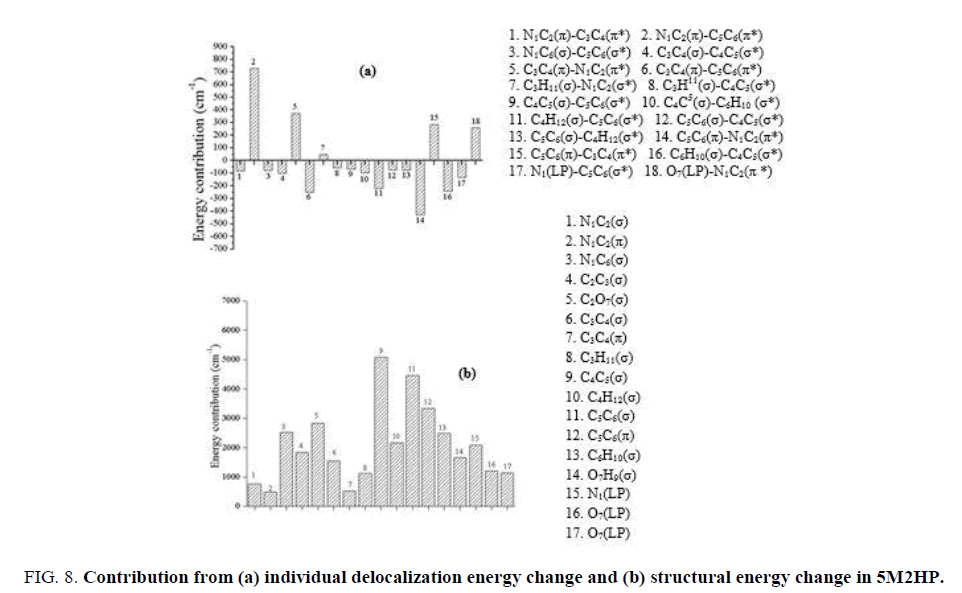
In the individual delocalization energy change as shown in FIG. 8a, the overall contribution is negative (-199 cm-1) and matched with the result shown in energy partitioned curve. The contributions from the π bonding orbital of C3C4 to the π antibonding orbital of N1C2 is cancelled out by the contributions from the σ bonding orbital of C5C6 and C4H12 and σ antibonding orbital of C5C6. The contribution from the interaction of π bond orbital of N1C2 with π anti-bond orbital of C5C6 is observed as the highest contributing term. The overall contribution from the σ components is negative hence the π component contributions play an important role in stabilization of the molecule. The structural energy change is shown in FIG. 8b. The overall change in structural energy is observed as positive as obtained in previously discussed molecules and does not match with the result shown in partitioned curve. The Lewis energy change can be calculated by calculating the change in structural energy and change in steric energy. Hence, in the contribution from change in steric energy is very important in determining the total Lewis energy. The major contribution is observed due to the contribution from σ components of bonds adjacent to the methyl group. In this molecule, the σ bond contribution is the dominant factor.
6-methyl-2-hydroxypyridine
In 6-methyl-2-hydroxypyridine, the methyl group has one N-C single bond and one C-C double bond adjacent to it. Hence the in-plane CH bond of methyl group is eclipsed towards the C-C double bond due to the higher π bond order. The change in geometrical parameters with respect to 2-hydroxypyridine is listed in TABLE 8. The major change observed as increase in C5C6 by 0.0054Å whereas decreases in N1C2 by 0.0020Å. This change could be because of the opening of the ∠C4C5C6 .
| Bond length | In Å | Bond angle | In degree |
|---|---|---|---|
| N1C2 | -0.0031 | ∠N1C2C3 | 0.1642 |
| C5C6 | 0.0054 | ∠C2C3C4 | -0.5358 |
| C2O7 | 0.0011 | ∠C3C4C5 | 0.2495 |
| - | - | ∠C4C5C6 | 0.8725 |
| - | - | ∠N1C2O7 | -0.141 |
Table 8: Change in geometrical parameters after substitution on 2HP in 6M2HP.
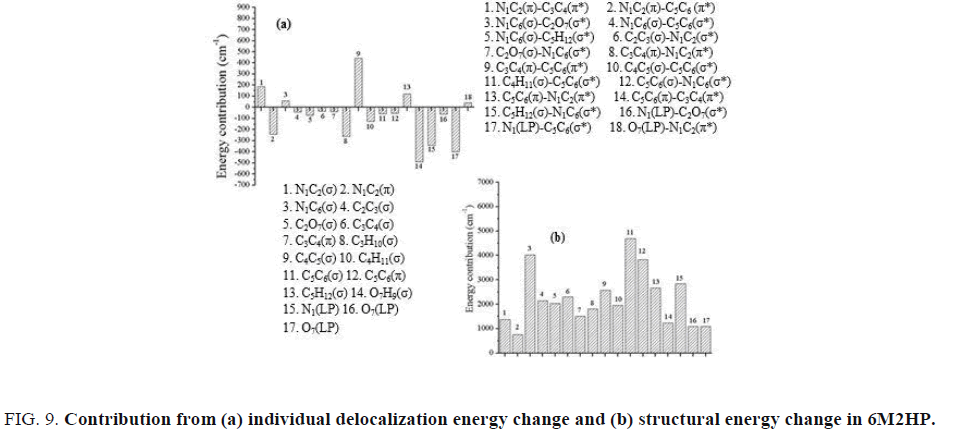
The change in individual delocalization energy of 6M2HP relative to 2-hydroxypyridine is shown in FIG. 9a. The overall contribution from the change in delocalization energy was observed as negative (-1357 cm-1). This is in accordance with the obtained result during partitioning the total energy into Lewis and non-Lewis terms. Due to the attachment of methyl group at C6 position, the lone pair interaction plays significant role in stabilization. As shown in FIG. 9a, the major contribution is from the local environment of methyl group.
The structural energy change in 6-methyl-2-hydroxypyridine is shown in FIG. 9b. The overall contribution is positive as observed in all other substituted molecules. Thus, in a similar manner, the change in steric energy plays an important role in determining the total Lewis energy as discussed earlier for other molecules. The major contribution is observed because of the σ bond component. The contribution from the adjacent bonds of methyl group also plays an important role and act as a stabilizing factor.
Conclusion
B3LYP/TZVP level of theory has been used for the study of 2-hydroxypyridine and its methyl substituent’s in ground electronic state. In the minimum energy conformation, the change in total energy was found to minimum for 6-methyl-2-hydroxypyridine whereas maximum for 5-methyl-2-hydroxypyridine in ground electronic state. The nuclear-electron (Vne) interaction energy is responsible for the stabilization of the methylated 2-hydroxypyridines in minimum energy conformation. The interplay of the various energies play key role in stabilizing the molecular structure in ground as well as in excited state. The steric energy is an important factor to overwhelm the Lewis energy. The local interaction of methyl group is the responsible term for the delocalization energy contribution.
Acknowledgement
This work was supported by the Department of Science and Technology (DST), India.
References
- Hazra MK, Chakraborty T. 2-Hydroxypyridine↔2-pyridone tautomerization: catalytic influence of formic acid. The J Phy Chem. 2006;110(29):9130-6.
- Friedberg EC. DNA damage and repair. Nature. 2003;421(6921):436.
- Rasmussen RE, Painter RB. Evidence for repair of ultra-violet damaged deoxyribonucleic acid in cultured mammalian cells. Nature. 1964;203(4952):1360.
- Setlow RB, Carrier WL. The disappearance of thymine dimers from DNA: An error-correcting mechanism. Proceedings of the National Academy of Sciences. 1964;51(2):226-31.
- Wang J, Boyd RJ. Tautomeric equilibria of hydroxypyridines in different solvents: An ab initio study. The Journal of Physical Chemistry. 1996;100(40):16141-6.
- Sobolewski AL, Adamowicz L. Photophysics of 2-Hydroxypyridine: an ab initio study. The Journal of Physical Chemistry. 1996;100(10):3933-41.
- Nimlos MR, Kelley DF, Bernstein ER. Spectroscopy, structure, and proton dynamics of 2-hydroxypyridine and its clusters with water and ammonia. The J Phy Chem. 1989;93(2):643-51.
- Frisch MJ, Trucks GW, Schlegel HB, et al. Gaussian 09, revision a. 02, gaussian. Inc., Wallingford, CT. 2009;11:200.
- Allouche AR. Gabedit: A graphical user interface for computational chemistry softwares. J Computational Chem. 2011;32(1):174-82.