Image Article

, Volume: 14( 1)

• View PDF
• Download PDF

Could We Forecast the High Energy Solar Flares Using Neutrino Detectors of the Second Generation?

*Correspondence:

O.M. Boyarkina
Department of Space Exploration, Belarusian State University, Dolgobrodskaya Street 23, Minsk, 220070, Belarus
E-mail: univerzumkaorelativnanula@gmail.com

Abstract

The physics physics-based method of forecasting the high energy Solar Flares (SFs) with the help of the neutrino detectors utilizing the Coherent Elastic Neutrino Neutrino-Nucleus Scattering (CEνNS) is considered. The behavior of the neutrino beams traveling through the Coupled Sunspots (CSs) being the source s of the future SFs is investigated. Two neutrino beams are included into consideration, namely, the ν_eL beam and the ν_µL beam which have been produced after the passage of the Micheev-SmirnovSmirnov-Wolfenstein resonance. It is assumed that the neutrinos possess the charge radius, the magnetic and anapole moments while the CS magnetic field is vortex, nonhomogeneous and has twisting. Estimations of the weakening of the neutrino beams after traversing the resonant layers are given. It is demonstrated, that this weakening could be registered by t he detectors employing CEνNS only when the neutrinos have the Dirac nature.

Keywords

Solar flares; Forecasting the flares; Neutrino oscillations oscillations; Magnetic moment moment; Anapole moment moment; Charge neutrino radius radius; Neutrino detectors detectors; Coherent elastic neutrino neutrino-nucle us scattering scattering; RED-100.

Introduction

Solar Flares (SFs) are the most striking explosive form of solar activity. They take place in the solar atmosphere and release a wealth of energy, which could be as large as 10²⁸-10³³ erg. Moreover, the super SFs with the energy of 10³⁶ erg and more are also possible in the solar conditions [1]. The SFs are often (but not always) followed by coronal mass ejections which represent eruptions of the solar coronal plasma into the interplanetary space. It is clear that the high energy SFs are very destructive when they are focused on the Earth as it was in 1859 [2]. It might be worth pointing out that the flares may be also occurred in other Sun-like stars. Flares at these stars are also dangerous for crew members of interplanetary spaceships. Therefore, for our ever more technologically dependent society forecasting the SFs has a large practical value.

It is generally accepted that the magnetic field is the basic energy source of the SF [3,4]. The course of the periods of the high solar activity, the magnetic flux ?10²⁴ G·cm² [5] is erupted from the solar center and stored on the sunspots. In so doing, big sunspots of opposite polarity could be paired forming, the so-called, Coupled Sunspots (CSs). Then accumulation of the magnetic energy starts. The more energetic the SF, the more will be the magnetic field strength of the CS. For example, in the case of the super SFs Bcs may reach the values of 10⁸ G and upwards. The length of the initial SF stage is extended from several to dozens of hours. Obviously, the successful SF forecasting should be based on the analysis of the phenomena occurring in the CS region at the initial stage of the SF. Previous studies of forecasting the SF are carried out with a help of γ-telescopes which observe the Sun collecting particle measurements related to SFs. Further, this huge amount of observations is transferred, stored, and handled. To deal with this data, a new method of Machine Learning (ML) has been created. The ML method has been utilizing such as models, as support vector machines [6], neural networks [7], a regression model [8], an extremely randomized trees [9] and so on. It was proposed to use satellites in the solar orbit with built in the ML capability that continuously monitor the Sun. These observatories will use the ML to calculate the probability of the solar explosions from the remote sensing data. Currently in operation are the following space-borne instruments: Solar and heliospheric observatory, solar dynamics observatory, advanced composition explorer, atmospheric imaging assembly, large angle spectroscopic coronagraph on the solar and heliospheric observatory. The ML can clarify which feature is most effective for forecasting the SFs. However, to date, it is not known which of the models used in the ML is the best.

Among the physics-based models that are used for forecasting the SF, the so-called kappa scheme proposed by a team of Japanese physicists [10] should be noted. Their model forecasts the high energy SFs through a critical condition of magneto hydrodynamic instability, triggered by magnetic reconnection. The group tested the method using observations of the Sun from 2008 to 2019. In the most cases, the method correctly identifies which regions will produce the high energy SF within the next 20 hours, the method also provides the exact location where each the SF will begin and limits on how powerful it will be.

The Sun is not only the source of electromagnetic radiation; it also emits a huge stream of electron neutrinos (N_νeL ≃ 6 × 10¹⁰ cm⁻² s⁻¹). It is obvious that with the help of sensitive neutrino detectors it will be possible to obtain information about events occurring in the CS region. It could be done with the detectors of the second generation whose work is based on coherent elastic (anti)neutrino-atomic nucleus scattering (CEνNS). This type of low-energy (anti)neutrino interaction was predicted in 1974 [11, 12] and was recently discovered by COHERENT Collaboration [13]. It was shown that neutrinos and antineutrinos of all types can interact by exchanging the Z-boson with the atomic nucleus as a whole, i.e. coherently. This take place with the (anti)neutrino energy being less than 50 MeV when De Broglie wavelength increases to the value of order of the nucleus charge radius R=1.12 × (A)^1/310⁻¹³ cm (A is the number of nucleons). The cross section of the CEνNS is described by the formula

σ ≃ few × 10⁻⁴⁵N²(Eν)²cm²,

Where, N is the number of neutrons, Eν is the (anti)neutrino energy, expressed in MeV. Thanks to the N2 factor, the cross section of this process is large, it is more than two orders of magnitude (for heavy nuclei) larger than the cross section of other known processes describing the interactions of low-energy (anti)neutrinos. To satisfy the demands for a coherently enhanced interaction, (anti)neutrinos need to be have energies in the MeVregime. As of now, the two favored antineutrino sources are nuclear reactors (Connie, Conus, Ncc-1701) and πDAR sources (Coherent, Ccm, Ess). These antineutrino sources taking together allow us to investigate different aspects of CEνNS at various energies and neutrino flavors.

Detectors based on the employment of the CEνNS are already being used for monitoring the operation of a nuclear reactor in the on-line regime. Examples are found in Russian Emission Detector-100 (RED-100) at Kalininskaya nuclear power plant [14]. Installed at a distance of 19 meters from a nuclear reactor, where the reactor antineutrino flux reaches the values 1.35 × 10¹³ cm⁻² c⁻¹, RED-100 should record 3300 antineutrino events per day. Moreover, in the future, it is planned to scale the detector by a factor of 10 to the mass of the sensitive volume of the order of 1 ton (RED-1000) [15]. This will make it possible to register 33,000 events per day. Obviously, such detectors can be also developed for observations of solar neutrinos (but here we shall deal with the coherent elastic neutrino-atomic nucleus scattering). Then, if to study the behavior of the solar pp neutrinos the detector similar in design to the RED-1000 will be used, then it could register about 2000 neutrino events per day.

The aim of our work is to investigate the possibility of forecasting the high energy SF with the help of the neutrino detectors utilizing the CEνNS. The work represents continuation of the papers [16-19] in which the correlation between the SF and behavior of the electron neutrino beam in the CS magnetic field during the initial stage of the SF was discussed. In contrast to the previous works, we take into account all the neutrino multipole moments and carry out the analysis for the Dirac and Majorana neutrinos. In the next Section constraining by two flavor approximation we obtain the evolution equation and find all the resonance conversions both of the electron neutrinos and of the muon neutrinos that emerged from the MSW resonance in the convective zone of the Sun. Further we give estimations of weakening the neutrino beam after traversing the resonant layers and demonstrate that this quantity could be observed by the neutrino detector of the second generation. Finally, in section 3, some conclusions are drawn.

In the Standard Model (SM) the neutrino magnetic moment is determined by the expression

It clear that such a small value cannot bring to any observable effects in real magnetic fields. Hence, if we use the values of the neutrino MMs being close to the upper experimental limits (10⁻¹⁰−10⁻¹¹) μB, then we should go beyond the SM. As an example of such a SM extension we may employ the left-right symmetric model which is based on the SU (2)R × SU (2)L × U (1)B−L gauge group [20]. In the one-photon approximation, the effective interaction Hamiltonian satisfying the demands both of the Lorentz and of the electromagnetic gauge invariance is determined by the following expression.

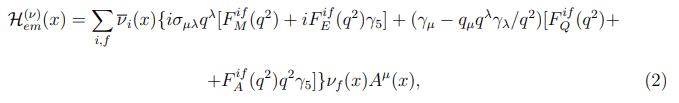
where q_μ=p′μ−pμ is the transferred 4-momentum, while F^ifQ, F^ifM, F^ifE, and F^ifA are the charge, dipole magnetic, dipole electric, and anapole neutrino form factors. The formfactors with i=f (i ?=f) are named” diagonal” (”off-diagonal” or ”transition”) ones. In the static limit (q²=0), F ^if M (q²), F^ifE (q²) and F^ifA (q²) determine the dipole magnetic, dipole electric and anapole moments, respectively. Note, the second term in the expansion of the Fif Q (q²) in series of powers of q2 determines the neutrino charge radius.

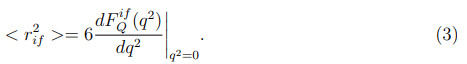
In what follows, we shall be interested in the Magnetic Moments (MM), the Anapole Moments (AM) and the Charge Radii (NCR). The exhibiting of neutrino MMs are being searched in the reactors (MUNU, TEXONO and GEMMA), the accelerators (LSND), and solar (Super-Kamiokande and Borexino) experiments. The current best sensitivity limits on the diagonal MMs gotten in laboratory experiments are as follow

μ^expee ≤ 2.9 × 10⁻¹¹μB, 90% C.L. [GEMMA] [25],

μ^expμμ ≤ 6.8 × 10⁻¹⁰μB, 90% C.L. [LSND] [26]

For the τ-neutrino, the limits on μττ are less limitative (see, for example), and the current upper bound on that is 3.9 × 10⁻⁷μB. The limits on the NCRs could be received from the studying the elastic neutrino electron scattering. For example, investigation of this process at the TEXONO experiment results in the following bounds on the NCR.

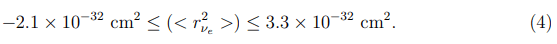
The AM of 1/2-spin Dirac particle was introduced in the work for a T-invariant interaction which violates P-parity and C-parity, individually. Later in order to describe this kind of interaction a more general characteristic, the toroid dipole moment (TM), was entered. It was shown that the TM is a general case of the AM and at the mass-shell of the viewed particle the both moments coincide. The neutrino toroid interaction are manifested in scattering of the neutrinos with charged particles. In so doing, the interaction saves the neutrino helicity and gives an extra contribution, as a part of the radiative corrections. In this regards, the AM is similar to the NCR. Both quantities preserve the helicity in coherent neutrino collisions, but have various nature. They define the axial-vector (AM) and the vector (NCR) contact interactions with an external electromagnetic field, respectively. From the viewpoint of determining the NCR and AM the low-energy scattering processes are of special interest. The both neutrino interactions may have very interesting consequences in various media. The possible role of the AM in studying the neutrino oscillations was first specified in Reference 33. A point that should be also mentioned is Reference 34 in which the existence of the AM led to the changing the flux of the solar electron neutrino during the initial stage of the SF. Since phenomenology of the AM is analogous to that of the NCR, the linkage between these quantities must exist. In the SM for a zero-mass neutrino, the value of the AM aν is connected with the NCR through the simple relation.

(the dimensionality of the AM in CGS system is” length²×charge”, that is to say, aν=ea′ν [29]). However, in the SM with the massive neutrinos and in the case of the SM extensions this relationship is violated.

As for the CS magnetic fields, we shall assume that they are nonhomogeneous, vortex and have the geometrical phase Φ(z) (twisting)

where Φ(z)=arctan (By/Bx). We notice that both for the Sun and for the Sun-like stars the reason of twisting is differential rotation rates of their components and the global convection of the plasma fluid. It should be recorded that configurations of the solar magnetic field implying twisting nature are already being discussed in the astrophysical literature for a long time. The phase Φ was introduced for the solar neutrino description for the first time. Subsequently, an account of this phase was demonstrated. It should be remarked the works which were devoted to the effects on neutrino behavior in the twisting magnetic fields. For example, the neutrino beam traveling in the twisting magnetic fields of the solar convective zone was considered and some new effects (changing the energy level scheme, changing the resonances location, appearing the new resonances, merging the resonances and so on) were predicted. Assuming that the magnitude of the twist frequency Φ? is determined by the curvature radius r0 of the magnetic field lines, Φ? ∼ 1/r,while r0 has the order of 10% of the solar radius, the authors came to the following conclusion. To ensure that these new effects will be observed the value of Φ? in the convective zone should have the ? order of 10⁻¹⁵ eV.

Insamuch as we shall take into investigation the interaction of the neutrinos with the electromagnetic fields, the neutrino system under study must contain both the left-handed and right-handed neutrinos. By virtue of the fact that the right-handed Majorana neutrinos are not sterile and interact as the right-handed Dirac antineutrinos, we shall denote them as νlR. In order to stress the sterility of right-handed Dirac neutrinos we shall use for them the notation νlR. So, in two-flavor approximation the Majorana neutrino system will be described by the function (ψ^M)^T=(ν_eL, ν_κL, ν_eR, ν_κR) while for the Dirac neutrinos we shall deal with the function (ψ^D)^T=(νeL, ν_κL, ν_eR, ν_κR). In what follows to be specific, we shall reason κ=μ. To facilitate the evolution equation for the solar neutrinos we transfer to the Reference Frame (RF) which rotates with the same angular velocity as the transverse magnetic field. The matrix of the transition to the new RF has the view

Where

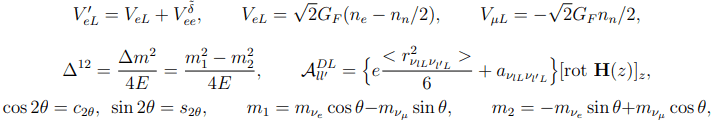
V_eL (V_μL) is a matter potential caused by interaction of the ν_eL (ν_μL) neutrinos with the gauge bosons W− and Z, V_δ˜ee is contribution to the matter potential produced by the singly charged Higgs boson ˜δ−, θ is a neutrino mixing angle in vacuum, m₁ and m₂ are mass eigenstates, ?Φis the twisting frequency, nn (ne) is neutron (electron) density and the free Hamiltonian covers interaction with medium.

When writing H^D_int we have taken into consideration that the toroid interaction does not equal to zero in the external inhomogeneous vortex magnetic field. In a concrete experimental situation this field may be realized according to Maxwell’s equations as the displacement and conduction currents. The universally adopted model of the SF is the magnetic reconnection model 4. Owing to it, a variable electric field induced by variation of the CS magnetic field appears at the SF initial phase. This field causes the conduction current which takes on the appearance of a current layer aimed at the limiting strength line which is common for the both CSs. So, in this case the neutrinos are influenced by both the displacement current and the conduction current. For the Majorana neutrino case the evolution equation will look like

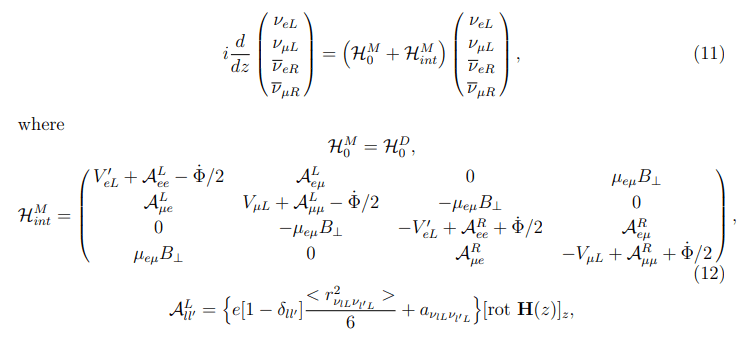
Our next task is to investigate the resonance transitions of the neutrino beam traveling the magnetic field of the CS which is the source of the future SFs. Remember, that for the resonance transition to occur, the following requirements must be met:

•The resonance condition must be carried out;
•The width of the resonance transition must be nonzero;
•The neutrinos must transit a distance comparable with the oscillation length.

In order to find the exact expressions for the resonance conversion probabilities we should specify the coordinate dependence of the quantities n_e, n_n B_⊥, Φ and solve the evolution equation. Then, with the help of the found functions νl(z), we could determine all resonance conversion probabilities. Of course we shall be dealing with numerical solution and, as a result, the physical meaning will be far from transparent. Moreover, in the most general case some of the resonance transitions may be forbidden. Therefore, first we must establish which of these transitions are allowed and which are forbidden. Further we shall follow generally accepted scheme, namely, we shall believe that all resonance regions are well separated what allows us to put these resonances independent. As far as the twisting is concerned, amongst existing the twisting models we choose the simple model proposed.

where α is a constant and Lmf is a distance on which the magnetic field exists. We begin with the resonant transitions of the νeL neutrinos in the Dirac neutrino case. Here the ν_eL may experience three resonance transitions. The first one is the ν_eL→ν_μL resonance transition. The requirement of the resonance existence, the width of the transition and the oscillation length are given by the expressions

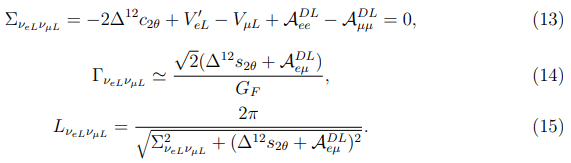
From Equation (14) and (15) it follows that the oscillation length reaches its maximum value at the resonance

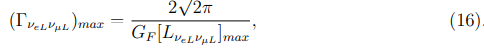
By virtue of the fact that (Γ_νeL_νμL)_max 3.5 × 10⁷ cm, this resonance transition is realized before the convective zone. Therefore, it is unrelated to the SFs which occurs in the solar atmosphere. That, in its turn, means that under the MSW resonance the quantities
A^DL_ee, A^DL_μμ and A^DL_eμ play no part. Estimation of the transition probability at the MSW resonance could be fulfilled with the help of the Landau-Zener formulae which in the case of the linear dependence of density on distance.

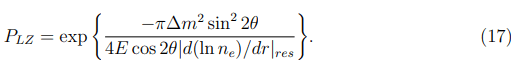
Then using P_LZ it can be shown that the neutrino flux passing through the region of this resonance must be reduced by about a factor of two as it was verified by experiments. Further we cross to treating the resonances of the ν_eL neutrinos traversing the CS magnetic field. In that case the ν_eL neutrinos may experience the following resonance transitions

ν_eL → ν_eR, ν_eL → ν_μR.

The quantities characterizing the ν_eL→ν_eR resonance transition are as follows

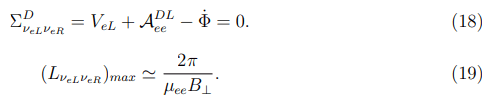
The case, when the term A^DL_ee is negligible compared to Φ and the resonance condition amounts to is unreal.

Genuinely, in order for Equation (18) to be satisfied, it is necessary that the twisting magnetic field exists at a distance greater than the solar radius. On the other hand, the currents producing the inhomogeneous vortex magnetic field could reach the values of 10⁻¹ A/cm². Then, for the CSs the quantity (a_νeLνeL) [rot H(z)]z will have the order of 10⁻³⁰ eV and being negative it could compensate the term of V_eL in Equation (18). In doing so the ν_eL→ν_eR resonance may take place only in the corona.

We are coming now to the ν_eL→ν_μR resonance. The pertinent expressions for this resonance will look like

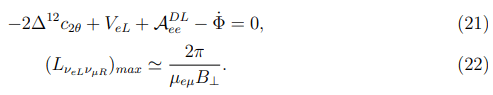
In the solar atmosphere, the term V_eL in Equation (21) are more less than Δ¹²_c2θ and play no part. Analogously the quantity (a_νeLν_eL) [rot H(z)]_z appears to be also small compared with Δ12_c2θ. Hence, the ν_eL→ν_μR resonance may take place only at the cost of the twisting, that is, when the relation will be realized.

Let us determine the values of the parameter α which provide the fulfilment of Equation (23) for different solar neutrinos. Assuming μ_eμ=μ_ee, B_⊥=10⁵ G and using for μ_ee its upper bound 2.9 × 10⁻¹¹μB we obtain

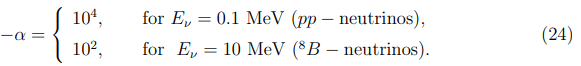
If the CS magnetic field increases to the value of 10⁸ G (as it may be for the super flare case [1]), the above mentioned values of |α| are decreased by a factor of 10³. Thus it becomes obvious that under the certain conditions the ν_eL→ν_μR resonance transition may be observed. The resonance condition (23) does not contain ne and nn and, as a consequence, the ν_eL→ν_μR resonance may occur both in the corona and in the chromosphere. Now we introduce the quantity which characterizes weakening the electron neutrino beam after traversing the resonant layer

η_νeLνμR=N_i–N_f/N_i

where N_i and N_f are numbers of the ν_eL neutrinos before and after the passage of the ν_eL→νμR resonance, respectively. Again, to find the exact value of ηνe_{LνμR w}e should concretize the dependence on distance of the quantities ne, nn, B⊥ and solve Equation (8). However, to roughly estimate this quantity, it will suffice to compare the resonance widths Γ_νeLνμL and Γ_νeLνμR, while taking into account the value of η_νeLνμL. Calculations result in

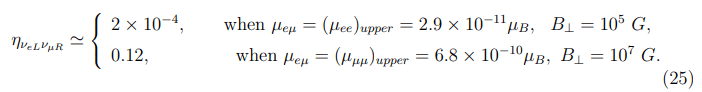
It should be noted that all the magnetic-induced resonances have the resonance widths which are completely determined by the quantity μ_νlνl′B_⊥. So, the foregoing estimations remain valid for such resonance conversions. Then it becomes evident that neutrino detectors utilizing the CEνNS could display weakening the νeL beam already at B_⊥ ≥ 10⁷ G.

Further we shall assume that the ν_eL beam has passed through the MSW resonance before entering the CS magnetic field. To put it another way, we shall deal with the beam which has been weakened at the cost of the ν_eL→ν_μL resonance. In the CS magnetic field, the νμL neutrinos produced due to the ν_eL→ν_μL resonance may experience the νμL→_νeR and νμL→_νμR resonance conversions. The corresponding resonance conditions will look like.

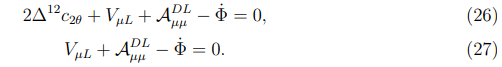
From Equation (26) follows that the ν_μL→ν_μR resonance appears to be allowed when

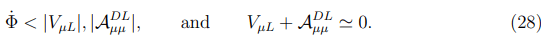
Note that in the conditions of the ν_μL→ν_eR and ν_eL→ν_μR resonances a large value of Δ¹²_c2θ could be compensated only by Φ. However, the fulfillment of the condition (26) ? requires that Φ be positive, while the condition (21) will be satisfied only if ? Φ is negative.

So, the survival probabilities of the electron and muon neutrinos are defined by the expressions:

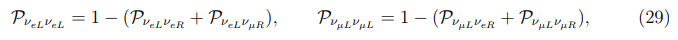
Where the contribution of the MSW-resonance has been eliminated for reasons expounded above. From the foregoing expressions follows that the AM and/or the NCR must be taken into account for the Dirac neutrino case. In what follows we shall discuss the oscillation picture for the Majorana neutrinos. Here for νeL we shall deal with the ν_eL→ν_μR resonance transition only. The relations being pertinent to this transition are as follows

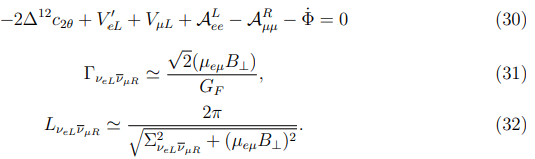
In the solar atmosphere, the terms V′_eL, V_μL and (a_νeLνeL + a_νμRνμR) [rot H(z)]_z appear to be small compared with Δ¹²_c2θ. Therefore, the ν_eL→ν^μR resonance may take place only at the cost of the twisting, that is, when the relation will be realized.

The oscillations picture will be incomplete, if we don’t take into consideration the oscillation transitions of the ν_μL neutrinos, which were produced due to the MSW resonance. In the CS magnetic field these neutrinos may experience the ν_μL→νe_{R r}esonance conversion. The corresponding resonance condition will look like

From comparing of the obtained expression with ΣνeLνμR it follows that when the ν_eL→ν_μR resonance will be forbidden then the ν_μL→ν_eR resonance is allowed, and vice versa. In that case the survival probabilities for the ν_eL and the ν_μL beams will be given by the expressions:

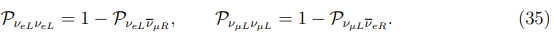
It should be also noted that from the obtained equations it follows that the contributions coming from the AM and the CNR can be safely neglected when the neutrino is the Majorana particle.

Conclusion

The physics-based method of forecasting the high energy Earth-directed SFs with the help of the neutrino detectors utilizing the CEνNS has been investigated. Consideration has been fulfilled within the left right symmetric model of the electroweak interaction. It was assumed that the neutrinos possess such multipole moments as the charge radius, the magnetic and anapole moments. In so doing we have constrained by two flavor approximation. The behavior of the neutrino beam traveling through the CSs being the sources of the future SFs has been discussed. It was speculated that the CS magnetic field is vortex, nonhomogeneous and possesses twisting. For the geometrical phase Φ(z) connected with magnetic field twisting Φ? (z) the simple model Φ?=exp[αz/Lmf ] has been employed.

Two neutrino beams are included into consideration, namely, the ν_eL beam and the ν_μL beam which has been produced after the passage of the MSW resonance. The investigations have been completed both for the Majorana and for the Dirac neutrinos. The evolution equation has been obtained in the Schrodinger-like form and all the possible magnetic-induced neutrino resonance transitions have been established.

It was shown that in the Majorana neutrino case the decreasing of the electron neutrino numbers is caused by the ν_eL→ν_μR resonance while decreasing the muon neutrino numbers is connected with the ν_μL→ν_eR resonance. Both these resonances may be in existence only when the CS magnetic field possesses twisting. It should be stressed that under the fulfillment of the ν_eL→ν_μR resonance condition appearance of the ν_μL→νe_R resonance is excluded, and conversely. Also note, that for the Majorana neutrino the AM and the NCF do not exert any influence on the values of the oscillation parameters at the conditions of the Sun. In the Majorana theory the right-handed neutrinos ν_μR and ν_eR are physical particles whereas detectors based on CEνNC are flavor-blind (at least with the existing experimental technique). Then, since the total neutrino flux is kept constant after traveling the resonances, the detectors will not feel the change in the flavor composition of the neutrino beam.

In the Dirac neutrino case the oscillation picture is richer. Here we have the following resonances ν_eL→ν_eR, ν_eL→ν_μR for the electron neutrinos, and ν_μL→ν_μR, v_μL →ν_eR for the muon neutrinos.

It should be stressed that in this case the ν_eR and ν_μR are sterile particles and they cannot be recorded by detectors based on CEνNC. The νeL→νμR and νμL→νeR - resonances could be realized only in the magnetic field with twisting, while the existing of the ν_eL→ν_eR and ν_μL→ν_μR - resonances are only possible if either or both the AM and the NCR have the values close to their experimental bounds. For all the magnetic-induced resonances the oscillation width depends on the quantity μ_ll′B_⊥ which, in its turn, determines the weakening of the neutrino beams traveling the CS magnetic field.

In this time, one should be expected that decreasing the electron neutrino beam will be less than decreasing the muon neutrino beam, since the upper bound on μμμ is bigger than that on μ_ee. Then, for example, using the upper bound on μμμ and assuming B_⊥=10⁸ G we shall get weakening of the νμL beam being equal to 1.2. It is obvious that the second generation detectors could observe such weakening the neutrino flux. Note, that the sensitivity of the measuring could be significantly improved when detectors with different element compositions are exploited. Then the systematic errors associated with the inaccuracy in determining the intensity of the neutrino beam are mutually excluded.

So, the detectors based on CEνNC could be utilized for forecasting the high-energy SFs only when the neutrino has a Dirac nature. This also allows us to state that the observation of the neutrino beams passing through the magnetic fields of the CSs, which are the sources of the SF, will allow to determine the neutrino nature.

The flares could occur in the Sun-like stars too. In that case the high energy flares exhibit the serious danger to the crew of the spacecraft. Consequently, the problem of forecasting the flare is topical for the cosmic flights as well. Obviously that terrestrial neutrino detectors will be of no avail when flying outside the solar system. It is hoped that the problem could find its solution with the help of neutrino detectors similar in design to the RED-100 installed on a spacecraft.

Acknowledgments

This work is partially supported by the grant of Belorussian Ministry of Education No 20211660.

References

1. Lingam M, Loeb A. Risks for life on habitable planets from superflares of their host stars. Astrophys J. 2017;848(1):41.

   [Google Scholar]

2. Carrington RC. Description of a singular appearance seen in the Sun on September 1, 1859. Monthly Notices Royal Astron Soc. 1859;20:13-15.
3. Shibata K, Magara T. Solar flares: magnetohydrodynamic processes. Living Rev Sol Phys. 2011;8(1):1-99.

   [Google Scholar]

4. Galloway DJ, Weiss NO. Convection and magnetic fields in stars. Astrophys J. 1981;243:945-953.

   [Crossref] [Google Scholar]

5. Qahwaji R, Colak T. Automatic short-term solar flare prediction using machine learning and sunspot associations. Solar Phys. 2007;241:195-211.

   [Google Scholar]

6. Ahmed OW, Qahwaji R, Colak T, Higgins PA, Gallagher PT, Bloomfield DS. Solar flare prediction using advanced feature extraction, machine learning, and feature selection. Solar Phys. 2013;283:157-175.

   [Google Scholar]

7. Lee JY, Moon YJ, Kim KS, Park YD, Fletcher AB. Prediction of daily maximum x-ray flux using multilinear regression and autoregressive time-series methods. J Korean Astron Soc. 2007;40(4):99-106.

   [Google Scholar]

8. Nishizuka N, Sugiura K, Kubo Y, Den M, Watari S, Ishii M. Solar flare prediction model with three machine-learning algorithms using ultraviolet brightening and vector magnetograms. Astrophys J. 2017;835(2): 156.

   [Google Scholar]

9. Kusano K, Iju T, Bamba Y, Inoue S. A physics-based method that can predict imminent large solar flares. Science. 2020;369(6503):587-591.

   [Crossref] [Google Scholar] [PubMed]

10. Freedman DZ. Coherent effects of a weak neutral current. Phys Rev D. 1974;9(5):1389.

    [Crossref] [Google Scholar]

11. Akimov D, Albert JB, An P, Awe C, Barbeau PS, Becker B. Observation of coherent elastic neutrino-nucleus scattering. Science. 2017;357(6356):1123-1126.

    [Crossref] [Google Scholar] [PubMed]

12. Akimov DY, Berdnikova AK, Belov VA, Bolozdynya AI, Burenkov AA, Dolgolenko AG, Tolstukhin IA et al. Status of the RED-100 experiment. J Instrum. 2017;12(06):C06018.

    [Google Scholar]

13. Boyarkin OM, Bakanova TI. Solar neutrino oscillations in extensions of the standard model. Phys Rev D. 2000;62(7):075008.

    [Google Scholar]

14. Pati JC, Salam A. Lepton number as the fourth" color". Phys Rev D. 1974;10(1):275.

    [Google Scholar]

15. Mohapatra RN, Pati JC. Left-right gauge symmetry and an" isoconjugate" model of CP violation. Phys Rev D. 1975;11(3):566.

    [Crossref] [Google Scholar]

16. Senjanovic G, Mohapatra RN. Exact left-right symmetry and spontaneous violation of parity. Phys Rev D. 1975;12(5):1502.

    [Crossref] [Google Scholar]

17. Nieves JF. Electromagnetic properties of Majorana neutrinos. Phys Rev D. 1982;26(11):3152.

    [Crossref] [Google Scholar]

18. Kayser B. Majorana neutrinos and their electromagnetic properties. Phys Rev D. 1982;26(7):1662.

    [Crossref] [Google Scholar]

19. Beda AG, Brudanin VB, Egorov VG, Medvedev DV, Pogosov VS, Shirchenko MV, Starostin AS, et al. The results of search for the neutrino magnetic moment in GEMMA experiment. Adv High Energy Phys. 2012(1):350150.

    [Crossref] [Google Scholar]

20. Auerbach LB, Burman RL, Caldwell DO, Church ED, Donahue JB, Fazely A. Measurement of electron-neutrino electron elastic scattering. Phys Rev D. 2001;63(11):112001.

    [Crossref] [Google Scholar]