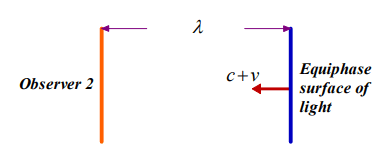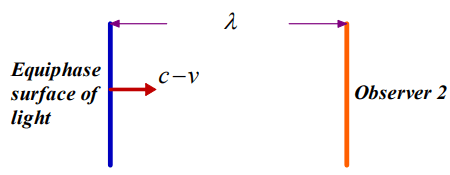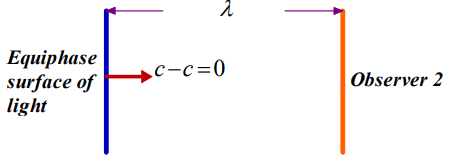Review
, Volume: 14( 2)Coordinate Transformations for the Optical Wave Equation
Abstract
A new coordinate transform is introduced for the wave equation, defined in different inertial reference frames. It is shown that two different measurement sets can be identified for a moving reference system with respect to the motionless observer. In one of these measurements, the speed of light does not change and has the same value with the velocity of light, propagating in the medium according to which the stationary observer rests. This behavior is also mathematically proven. Coordinate transformations are derived by using the wave equation and the phase term of its general solution. The behaviors of these transforms for different cases are studied.
Keywords
Wave equation; Speed of light; Relativity
Introduction
The speed of light, generally shown by the symbol c, depends on the electromagnetic properties of the medium, in which it propagates. These properties are the permittivity (ε) and permeability (µ) that show the electric and magnetic responses of the medium to the electromagnetic field respectively. Thus the speed of light is expressed by the formula 1/√µεdirectly. In fact, the reason of the null result, in the Michelson-Morley experiment, is hidden in this concept. In the 19th century, it was generally accepted (not a scientific attitude, because general acceptances are generally wrong as is shown by the history) that the light propagates in a conceptual medium, named ether. Michelson and Morley tried to determine the relative motion of the earth with respect to this medium [1]. They thought that the earth was moving and the ether was at rest. Thus an interference based set-up was constructed that was comparing two light waves propagating in perpendicular directions with respect to the motion of earth. However, the experimenters could not find any difference between the velocities of the light waves wherever they repeated the experiment. Thus they concluded that the speed of light was constant with respect to the inertial reference frames. The scientist of that era tried to explain the outcomes of the Michelson-Morley experiment according to the ether theory. As a result, Lorentz put forth a coordinate transformation system, named after him. His aim was to derive a transformation, which would lead to the same wave equation, between two inertial coordinate systems. Einstein's special theory of relativity is directly based on the Lorentz transformation. One of the main inferences of this theory was the ultimate limit of speed, which was the velocity of light in the universe. This result is directly related with the Lorentz transformation [2].
The motivation of this paper is to put forward that there is an alternative set of transformation for inertial reference systems. With this aim, we will consider two reference frames, one of which is moving with a constant speed and the other one is motionless. We will show that two cases can be defined for the coordinate system of the moving observer. Frequency and velocity equations will be derived by taking into account these two cases. The coordinate transformations will be obtained with the aid of the wave equation and the argument of the general solution of this equation. Such an approach is important in the sense of the relative and subjective measurements of moving observers with constant velocities. The physical implications and interpretations of the new coordinate transformations will be discussed [3].
Literature Review
The wave equation
The propagation of light, in a simple medium (linear and isotropic) medium is governed by the wave equation of
Equation
where u is a component of the electromagnetic field. Note that Equation. (1) is defined for a source- free region. The wave equation can be directly derived from the Maxwell’s equations. As mentioned in the Introduction, the speed of light c is equal to
Equation
which is a function of the permittivity and permeability of the medium [4]. Thus the velocity of light is determined by the medium in which it propagates [5]. The general solution of the wave equation can be expressed by
Equation
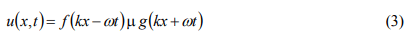
For a one spatial dimensional wave. f and g are arbitrary functions. k and ω are the wave-number and angular frequency respectively [6]. This equation can be obtained from the parametric solution of the wave equation. Equation (3) can be arranged as
Equation
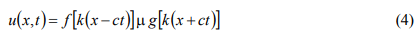
Where the speed of light is defined by
Equation
in terms of wave-number and angular frequency. We will use Equation. (1) and the arguments of the general solution, which can be expressed as
Equation
for the derivation of the coordinate transforms. Note that the wave-number is equal to
Equation
Where λ is the wavelength [4].
The mathematical foundations of the coordinate transformations
We take into account two reference frames as (x,t) and (x1,t1). The coordinate system of (x,t) is motionless and (x1,t1) is moving with a constant velocity of v according to (x,t). We assume the transformation set of
Equation
and
Equation
for α, a, b, d and e are constant coefficients that will be determined. The wave equation can be written by
Equation
and
Equation
for the reference frames of (x,t) and (x1,t1) respectively. c1 is the speed of light in the coordinate frame (x1,t1). One can object that c1 should be equal to c, but at this time and for the generalization of the results we assume it to be so. The function p, in Equation. (6), can also be written as
Equation
and
Equation
for (x,t) and (x1,t1) respectively. k1 is generally not equal to k because of the effects as the Doppler shift. The second derivatives of u, in Equation (10), according to x and time can be evaluated as
Equation
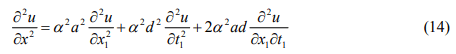
and
Equation
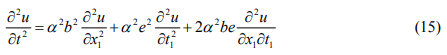
respectively. Equation (10) becomes
Equation
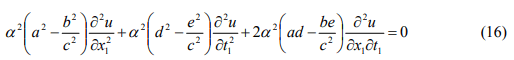
when Equations. (14) and (15) are used. The relations of
Equation
can be obtained when Equations. (11) and (16) are compared. The equation set of
Equation
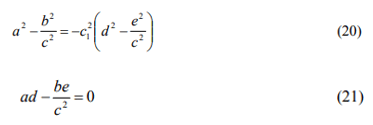
can be defined in order to obtain the Lorentz transformation. Of course, c1 is equal to c in this case. We will consider Equations. (17-19) in this study.
The coefficient a and d are determined to be
Equation
respectively. The equation of
Equation
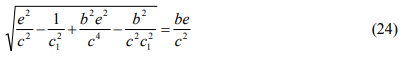
can be obtained from Equation. (21). The coefficient e is found to be
Equation
from Equation. (24). d is expressed by
Equation
in terms of b. As a result, the coordinate transform can be written as
Equation
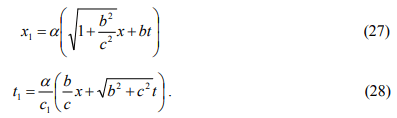
The function p, in Equation. (13), reads
Equation
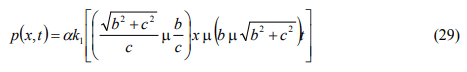
when Equation. (27) and (28) are taken into consideration. Equation (29) can be arranged as
Equation
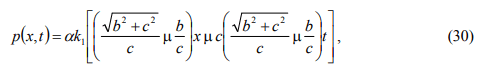
which yields the expression of
Equation
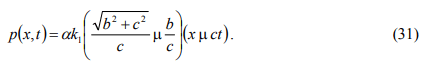
The coefficient α is found to be
Equation
when Equations. (12) and (31) are compared. As a result, the new coordinate transformation set is given by
Equation
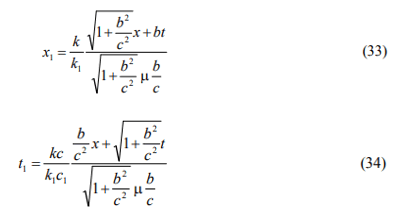
in terms of b, which will be determined in the next section. The inverse transformations can be derived in a similar manner. In this case, c and k replaces with c1 and k1 and vice versa. The set of inverse transformation can be written as
Equation
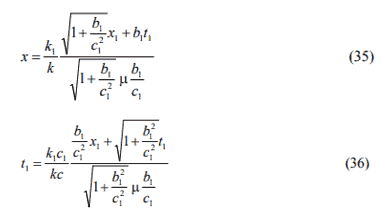
in terms of the coefficient b1.
Discussion
The coordinate transformations between inertial reference frames
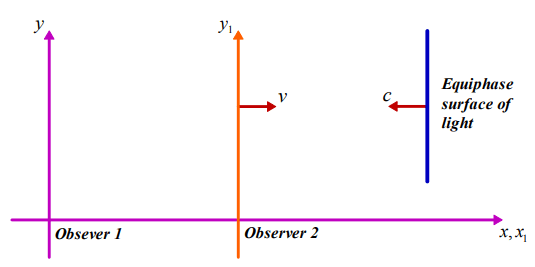
Two inertial reference frames are taken into account as shown in Figure 1. Observer 1, shown by (x, y, t) is motionless. The second observer, (x1, y1, t1) is moving with the constant velocity of v. The light is propagating in the stationary medium, in which Observer 1 is stationary. Thus according to this observer, its speed is equal to c.
FIG. 1. The geometry of the inertial reference frames.
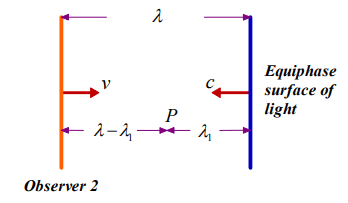
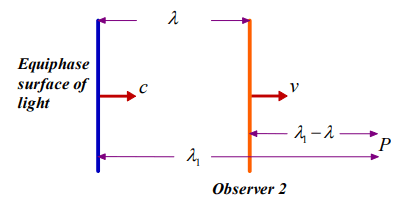
We can investigate two distinct cases for the scenario, in Figure 1. The first case is the evaluation of the observer 2’s measurement on light according to observer 1. In this situation, the geometry, in Figure 2, can be considered for the determination of light’s parameters.
FIG. 2. The measurement of observer 2 according to observer 1.
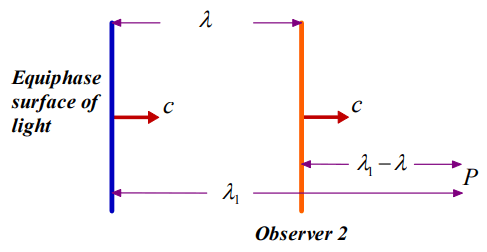
In Figure 2, observer 2 is in the same point with one of the equiphase surfaces of light. The distance, between the observer and the following surface is equal to the wavelength. The observer and the second equiphase surface will meet at point P at the same time according to the reference frame of the observer 1. Thus the relation of
Equation
can be written from the geometry. λ1 is found to be
Equation
from Equation (37). According to Observer 1, λ1 is the wavelength that will be measured by observer 2. The period of the light is equal to
Equation
which is also the arrival time of the observer 2 and the equiphase surface of light to point P. The frequency reads
Equation
and the speed of light, measured by observer 2 according to observer 1, is found to be
Equation
from the relation of vp=λf. vp is the phase velocity. The wave-number can be expressed as
Equation
which is also equal to
Equation
in terms of k, which is the wave-number according to observer 1. The coordinate transformations can be written as
Equation
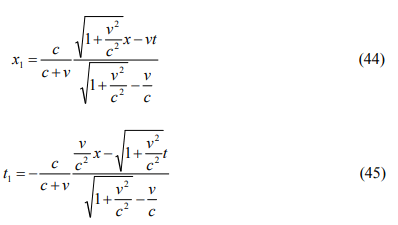
from Equations. (33) and (34). b is taken as -v, since observer 2 is moving away from observer 1. The plus sign is chosen from μ, because the light is approaching towards both of the observers. In the non-relativistic limit of c→∞, the transformations become
Equation
which are the well-known Galilean transformations for the geometry, in Figure 1. It is also important to note that the transform of
Equation
is valid for the relativistic and non-relativistic cases.
In the second case, we will investigate the direct observation of light by observer 2 and compose the coordinate transformation according to the parameters, obtained.
FIG. 3. The measurement of Observer 2 on light.
In this case, the measurement is being made from the reference system of observer 2. Thus this observer evaluates himself as standing still and the equiphase surface of the light reaches him quicker. Note that the light is propagating in a medium, which is stationary according to the reference frame of observer 1. If observer 2 was measuring the light, which is moving in his reference frame, he would find its speed as c. Thus the parameters λ1, f1, vp1 and k1 is determined to be
Equation
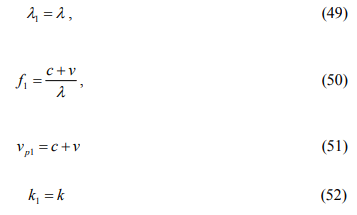
respectively. The coordinate transformations become
Equation
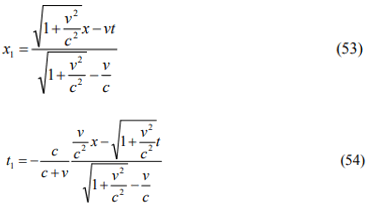
in this case. Note that Equations. (45) and (54) have the same expressions. Only, Equations. (44) and (53) are different.
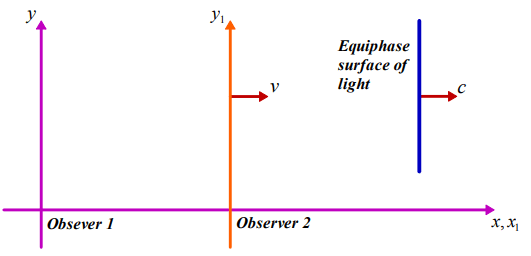
The geometry for the second scenario that will be investigated in this study is given in Figure 4. In this case, the light is propagating in the same direction with observer 2.
FIG. 4. The geometry of the inertial reference frames.
First of all, we will study the measurement of observer 2 with respect to observer 1.
The related geometry is shown by Figure 5.
FIG. 5. The measurement of observer 2 according to observer 1.
In the initial moment of measurement, observer 2 is in the same location with the first equiphase surface of light. The second equiphase surface will catch observer 2 at point P as shown in Figure 5. According to observer 1, observer 2 will measure the wavelength of light as λ1. The relation of
Equation
can be written from the geometry, in Figure 5. The relative wavelength λ1 can be evaluated as
Equation
from Equation. (55) in terms of the actual wavelength λ. The relative period and frequency of light is found to be
Equation
respectively. The relative speed of light can be expressed by
Equation
The relative wave-number can be determined as
Equation
in terms of the actual wave-number k. The phase function, in Equations. (12) and (13), are equal to
Equation
in this case. As a result, the coordinate transformations can be written by
Equation
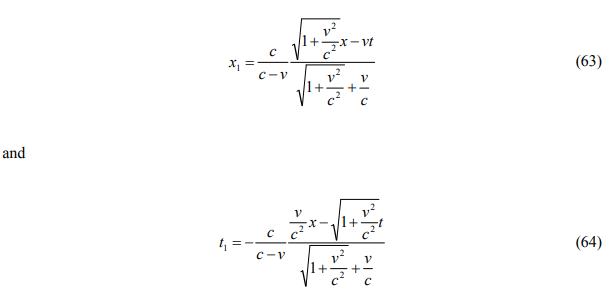
where the coefficient b is equal to -v. The spatial coordinate y1 is equal to y.
As the second case, we will investigate the observation, performed by observer 2. The geometry, in Figure 6, is taken into consideration.
FIG. 6. The measurement of observer 2 on light.
Observer 2 perceives that he is motionless and the light approaches him with the velocity of c-v. The wavelength, which is measured by the second observer is equal to the actual wavelength of light λ. The period, frequency and wavenumber can be expressed by
Equation
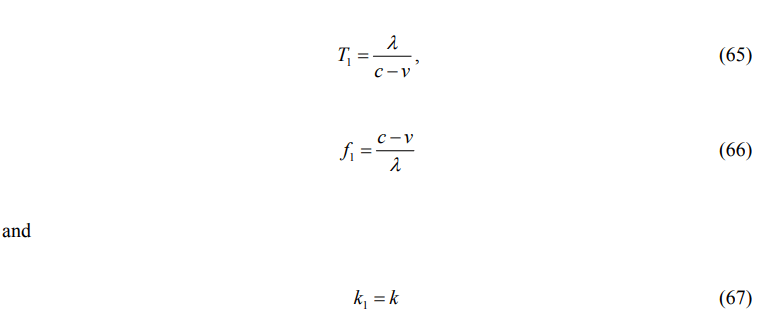
according to Figure 6 respectively. The phase velocity of light is equal to c-v. Thus the coordinate transformations become
Equation
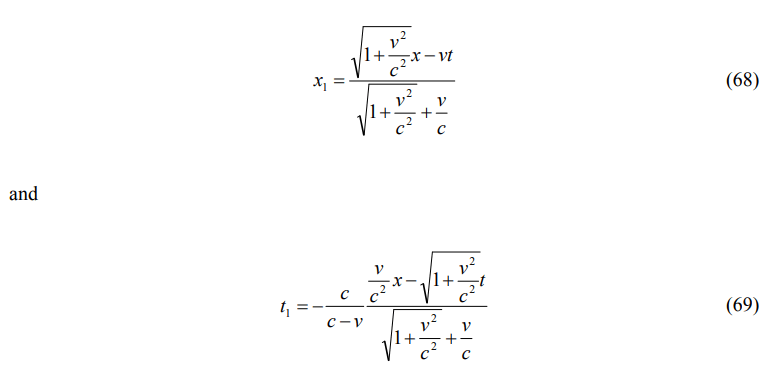
from Equations. (33) and (34) for this case.
The relative effect of velocity on time
In this section, we will analyze the effect of the velocity on time observations. The scenario, in Figure 1, is taken into account. In the first case, the frequency, wavelength and speed of light was measured according to observer 2, but with respect to the coordinate system of observer.
The obtained coordinate transformation can be given by
Equation
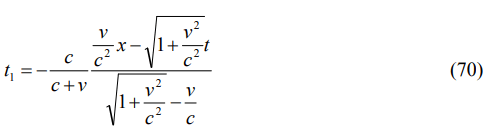
for time. Note that the observations give the same results as shown in Equations. (45) and (54). The Galilean and Lorentz transformations have the expressions of
Equation
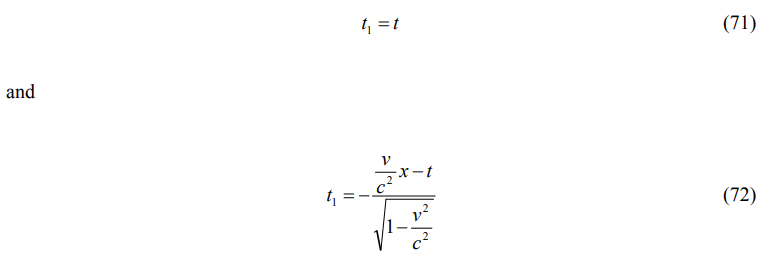
respectively.
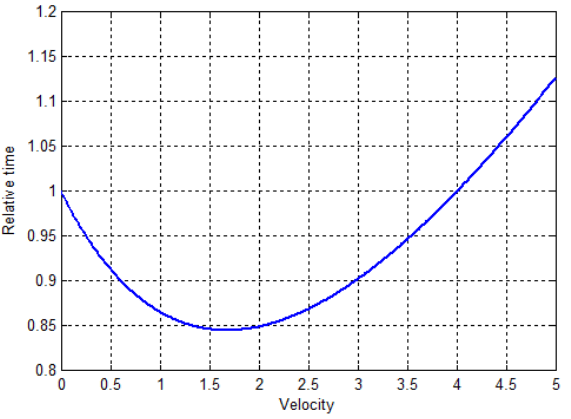
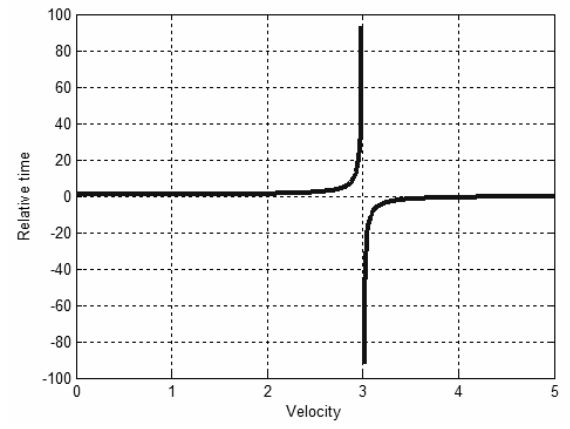
Figure 7 shows the variation of the relative time with respect to the velocity. The velocity is taken from zero to five without dimensions. The speed of light is accepted to be three. It can be seen from the figure that the time slows down till the velocity is equal to 1.65. Then it begins to accelerate with respect to the time frame of the motionless observer.
FIG. 7. The variation of relative time, in Equation. (70).
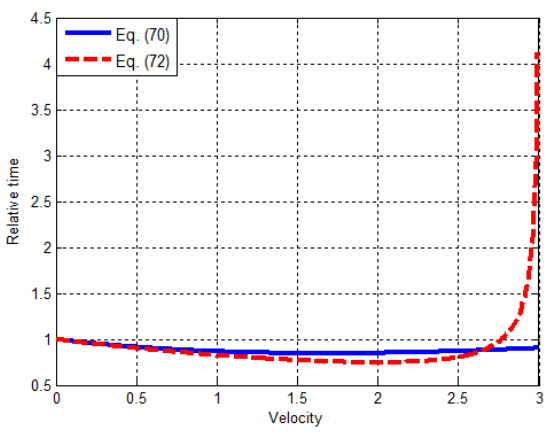
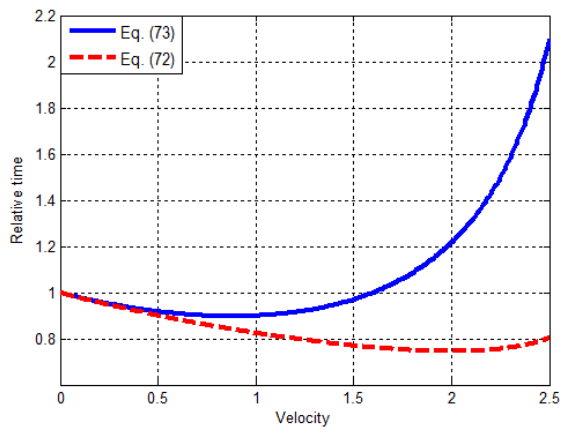
In Figure 8, the variations of the relative times, in Equations. (70) and (72), are compared. The Lorentz transform also shows a similar behavior with the one, derived in this study. However, the relative time approaches to infinity at the speed of light because of the term in the denominator of Equation. (72). This behavior does not have any physical meaning. As is well known, in physics the infinities are not acceptable and the mathematical expressions that give asymptotes are corrected or replaced with functions that give finite values at those points. The uniform expressions in edge diffraction and renormalization in quantum electrodynamics can be given as examples to this process.
FIG. 8. The comparion of relative times, in Equations. (70) and (72).
As the second case, we will investigate the scenario, in which the light moves in the same direction with both of the observers. The relative times had also same expressions for the scenarios, defined in the previous section. The equation can be given by
Equation
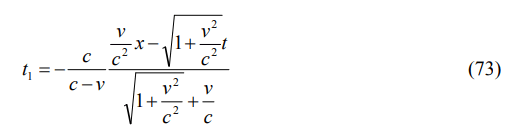
from Equations. (64) and (69). The Lorentz transformation has the same expression with Equation. (72) in this case.
In Figure 9, the variation of the relative time versus velocity is plotted. As can be seen from the figure, the time goes to infinity at the speed of light, because of the term c-v, in Equation. (73). This behavior is related with the scenario, shown in Figures 5 and 6. The period of the light is defined as the time, required for the arrival of phase front to the observer 2. When the velocity of the observer is equal to the speed of light, the equiphase surface will never be able to reach the observer. This also means that the arrival time of the wave-front to observer 2 is infinite. In order to represent this idea, the related figures are re-shown as Figures 10 and 11 for this case.
Equation
FIG. 9. The variation of relative time, in Eq. (73).
FIG. 10. The measurement of observer 2 according to observer 1 for the velocity is equal to the speed of light.
FIG. 11. The measurement of observer 2 on light for the velocity is equal to the speed of light.
Figure 12 shows the comparison of our formulation with the transformation of Lorentz. The two solutions approach to infinity at the speed of light, but our equation’s behavior is based on a physical explanation. Both of the relative times follow the same pattern which can be expressed by acceleration after slowing down. Equation (73) more rapidly approaches to infinity than the Lorentz transform. As mentioned above, this behavior is strictly related with the relative period of the light wave.
FIG. 12. The comparion of relative times, in Equations. (72) and (73).
Conclusion
In this paper, we derived novel coordinate transformations between two inertial reference frames. To our knowledge, these expressions have not been introduced in the literature yet. The transformations are based on the definition of the wave equation in the two reference frames. The results were studied numerically with respect to the relative time. The transformations are finite except one case, in which the relative time approaches to infinity when the velocity of a reference frame goes to the speed of light. It is shown that this behavior is related with the measurement of light and the physical meaning of the infinity is outlined in Figure. 10 and 11. This means that the wave front of light cannot catch the moving reference frame when its velocity is equal to the speed of light. These transformations can be thought as an alternative to the Lorentz transformations.
