Review

, Volume: 14( 3)

• View PDF
• Download PDF

Black Holes

*Correspondence:

Pastushenko Vladimir Alexandrovich Department of Space Exploration, Megatrend University, Beograd, Serbia, E-mail: past.vlad2@gmail.com

 

Abstract

We will talk about the properties of “black spheres” called “black holes”, within the framework of the properties of dynamic space-matter, which are subject to experimental testing. First of all, the presence of new quanta in the cores of planets, in the cores of stars, in the cores of galaxies, in the cores of quasars and in the cores of quasar galaxies. And first of all, stable quanta of the new substance.

Keywords

Dynamic space; Euclidean axi omatic Parallelism Length

Introduction

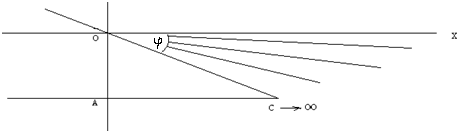
It is generally accepted (in 2020) that there is a “supermassive compact object in the center of the galaxy.” And there is the fact of the presence of dynamic space-matter within the always dynamic (φ ≠ const) angle of parallelism [1].

FIG. 1. Dynamic space of a bunch of parallel straight lines.

Literature Review

There is no matter outside space, and there is no space without matter, therefore space, as a form of matter, is one whole. Infinity (AC→∞) cannot be stopped, therefore such dynamic space-matter always exists. The limiting case ((φ=0)=const) of ((φ≠0) =const) dynamic space-matter is the Euclidean axiomatics and Riemannian space in particular [2].

• A point is something of which nothing is a part”) (“Principles” by Euclid). and is a point something that has no parts,

• Line-length without width.

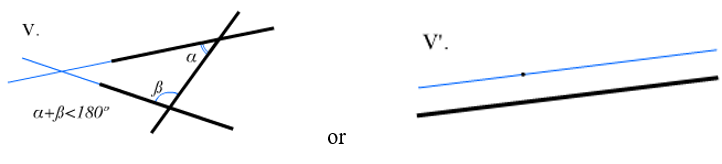
• and 5^th postulate about parallel straight lines that do not intersect. If a straight line intersecting two straight lines forms interior one-sided angles less than two right angles, then, extended indefinitely, these two straight lines will meet on the side where the angles are less than two right angles.

FIG. 2. Euclidean axiomatics.

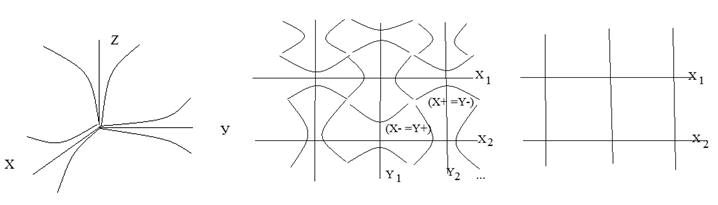
Within the framework of the Euclidean (φ=0) axes grid, we do not see dynamic (X+=Y-), (X-=Y+) space-matter and we will not be able to imagine it. Therefore, the axioms of dynamic space-matter are introduced as facts that do not require proof. Already in these axioms the problem of the Euclidean axiomatics of a point, as a set of indivisible sphere-points, is solved in one indivisible sphere-point, but already on (n) convergence, dynamic space-matter [3].

FIG. 3. Dynamic space-matter.

FIG. 4. Dynamic space-matter.

Any fixation (in experiments) of a non-zero (φ ≠ 0) angle of parallelism gives a multi-leaf Riemannian space. Now within the framework of the axioms of dynamic space-matter in the form:

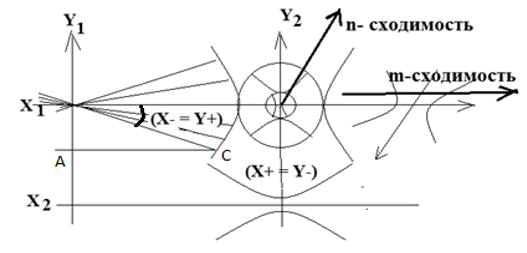
• A non-zero, dynamic angle of parallelism (φ ≠ 0) ≠ const, a beam of parallel straight lines, determines the orthogonal fields (X-) ? (Y-) of parallel lines - trajectories, as isotropic properties, of space-matter.

• Zero angle of parallelism (φ=0), gives a “length without width” with a zero or non-zero Y0 radius of a sphere-point “having no parts” in the Euclidean axiomatics.

• A bundle of parallel lines with zero angle of parallelism (φ=0), “equally located to all its points,” produces many straight lines in one “widthless” Euclidean straight line [4].

• Internal (X-), (Y-) and external (X+), (Y+) fields of line-trajectories are non-zero ?0 ≠ 0 or Y0 ≠ 0 material sphere-point, form an Indivisible Area of Localization HO? (X ±) or HO? (Y ±) dynamic space-matter.

• In unified fields (X-=Y+), (Y-=X+) orthogonal lines-trajectories, (X-) ? (Y-) there are no two identical sphere-points and lines-trajectories.

•A sequence of indivisible areas of localization, (X+), (Y+), (X+), ... along a radius ?0 ≠ 0 or Y0 ≠ 0

•?0≠0 or a sphere-point on one line-trajectory gives n convergence, and on different trajectories m convergence.

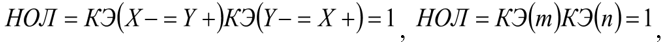
• Each indivisible area of localization of space-matter corresponds to a unit of all its evolution criteria - CE, in a single (X-=Y+), space (Y-=X+) –matter at m-n convergence in a system of numbers of units equal by analogy.

• Fixation of an angle (φ ≠ 0) ≠ const or (φ=0) a bundle of straight parallel lines, space-matter, gives Euclid's 5^th postulate and the axiom of parallelism [5].

Any point of fixed line-trajectories is represented by local basis vectors of Riemannian space:

with fundamental tensor 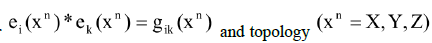Euclidean space. That is, Riemannian space is a fixed (φ ≠ 0) ≠ const state of dynamic (φ ≠ const) space-matter. Local basis vectors correspond to the velocity space WN =K+N T- N, in multidimensional space-time. Space-time is a special case of a fixed state of dynamic space-matter. At the same time, all Criteria for the Evolution of Matter are formed in multidimensional space-time.

They are presented in the “Unified Theory 2”, in the form of: (P=W²) potential, (F=P²) force, energy: charge PK=q (Y+ =X -) in electro (Y+=X-) magnetic fields, or mass PK=m (X+=Y-) in gravit (X+=Y-), mass fields, then density 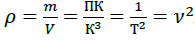is the square of frequency, energy E=P²K, impulse (p=P²T), action (?=P²KT)…, a single space-matter [6].

FIG. 5. Unified criteria for the evolution of space-matter.

Let us immediately note the “point that has no parts” in the Euclidean axiomatics, and the non-zero radius ?₀ ≠ 0 or Y₀ ≠ 0 material sphere-point of the axioms of dynamic space-matter. In addition, there is a minimum Planck length (λ=10^-33??). These are questions of singularity that are not here, plus the mathematical prohibitions of division by zero.

As part of a dynamic (φ ≠ const) space-matter, we have a non-stationary Euclidean space-time (X, Y, Z, cT), or a geodesic variable (?s ≠ const), fundamental tensor g_ik(?^s) Riemannian space. For example, the no stationary space of Lobachevski geometry, with variable asymptotes of hyperbolas. There is no such mathematics yet.

In other words, we will consider the issues of “black holes” in the axioms of Euclidean space-time, as a special case (φ=0) or ((φ≠0)=const) dynamic (φ ≠ const) space-matter.

Discussion

Assumptions: Within the framework of classical physics, even 100-200 years ago, and in the laws of conservation of energy

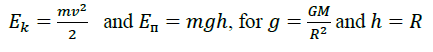
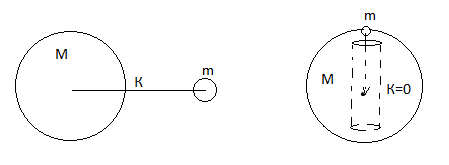
Earth, the maximum speed was determined: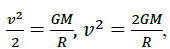 in which the body may not return to Earth (m). And even then, the hypothesis of super massive (m ≠0) “black stars”, from which light does not come out, arose. The sphere of such “black stars” 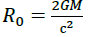was called the Schwarzschild sphere. The reason was considered to be Newton’s gravitational force, F=2GMm/R². Here
R is the distance between the centers of massive (m≠0) and (m≠0)massive spheres, the Earth and the Moon, for example. But if a small ball is lowered into the diametrical hole of a large massive sphere (??→0), then the force does not increase indefinitely.

FIG. 6. Newton's law.

Newton's law doesn't apply here. Newton introduced the very concept of force from the springy collision of two balls, with inverse proportionality to their accelerations of expansion.

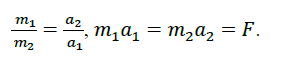
In other words, in Euclidean axiomatics it is impossible in principle to create the Quantum Theory of Relativity. Both theories: Special Theory of Relativity and Quantum Theory of Relativity, allow superluminal (vi=N*c) velocity space:

Already within the framework of such ideas, we will consider “black holes”. In classical physics with the Euclidean axiomatic of space-time, for super massive “black stars” (m≠0), with a gravitational radius, 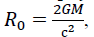of any mass in theory. And for the masses (m≠0)= const such a sphere, there must be a superluminal space of velocities (v_i >c) or ( v_i = n*c), ( N>1). This does not contradict either the Special Theory of Relativity or the Quantum Theory of Relativity. In the quantum coordinate system of the dynamic ( φ = const ) space-matter, we are talking about superluminal space of velocities vi= n*c where α=1/137,036 the constant.

But let's return to the laws of classical physics, in which Newton's law of gravity has limits of application, and did not answer the question WHY do masses attract? Studying Maxwell's equations, like electromagnetic fields with Lorentz transformations in two (x₀,y₀,z₀,ct₀) And (x₁,y₁,z₁,ct₁) coordinate systems, and from the laws of conservation of energy, back in 1905, Einstein derived a formula, which we will dwell on in more detail.

Body with non-zero(m≠0) mass, emits light with energy (m=0) in symte coordinates, with the law of conservation of energy: (E0=E1+L), before and after radiation. For the same mass in a different coordinate system, the law of conservation of energy with 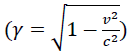Lorentz transformations, Einstein wrote in the _form (H0=H1+L/γ). Subtracting their difference, Einstein got:

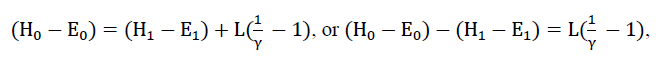
With separation of the radiation energy difference. Both inertial coordinate systems are moving, but (x₁,y₁,z₁,ct₁)moving at a speed (??) rlati (x₁,y₁,z₁,ct₁e) . And it is clear that blue and red light have an energy difference, which Einstein wrote down in the equation. Einstein wrote down the equation itself as the difference in kinetic energies in the first expansion.

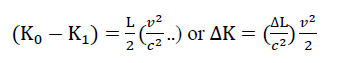
Here 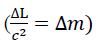the multiplier has the properties of the “radiant energy” mass, or: ΔL=Δcm². This formula has been interpreted in different ways. The annihilation energy of E=m₀c²the rest mass, or: 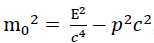in relativistic dynamics. Here is the mass with zero momentum(?=0), has and the zero mass of _the photon: (m0=0), momentum and energy

E=P*C Einstein derived another law of “radiant energy” (ΔL=Δmc²), with mass properties. This is not the energy of a photon, and this is not the energy of (ΔE= Δmc²)a defect in the mass of nucleons in the nucleus of an atom. Einstein saw something that no one else saw. Like a moving charge, with the magnetic field induction of Maxwell's equations, a moving mass induces mass energy , which is what Einstein found. For example, a charged sphere inside a moving carriage has no magnetic field. But the compass on the platform will show the magnetic field of the sphere in the moving carriage. It was precisely this kind of inductive magnetic field, from the moving electrons of a conductor current, that Oersted discovered. Then there were Faraday's experiments, the induction of vortex electric fields in an alternating magnetic field, the laws of induction and self-induction, and Maxwell's equations. By analogy with the inductive energy of a magnetic field from a moving charge, Einstein derived the formula for the inductive, “radiant” energy of mass fields from moving non-zero masses, including stars in galaxies. And here Einstein went beyond the Euclidean (φ=0)axiomatics of space-time. In the axioms of dynamic space-matter (φ= const), we are talkinabout inductive m(Y^-)mass fields, in complete analogy with Maxwell’s equations. This is what Einstein saw, and no one else. Already from the Equivalence Principle, the potential of the inductive mass field

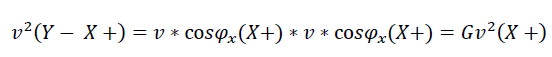
in a gravitational field, a constant follows (G=cos²φx)as a mathematical truth. And already writing the equation of the General

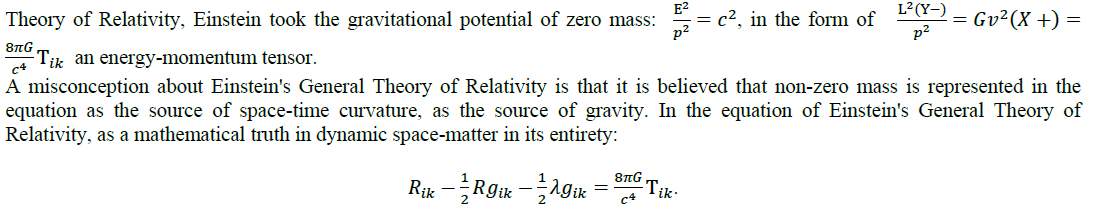
There is no mass: (m=0), in its classical sense. In mathematical truth, this is the difference in relativistic dynamics at two fixed points in Riemannian space, one of which is reduced to the Euclidean sphere, in the external, non-stationary (λ≠0) Euclidean space-time. In physical truth, in the equation of the General Theory of Relativity, Einstein, in the unified Criteria of Evolution, Newton’s formula (law) is “hardwired”:

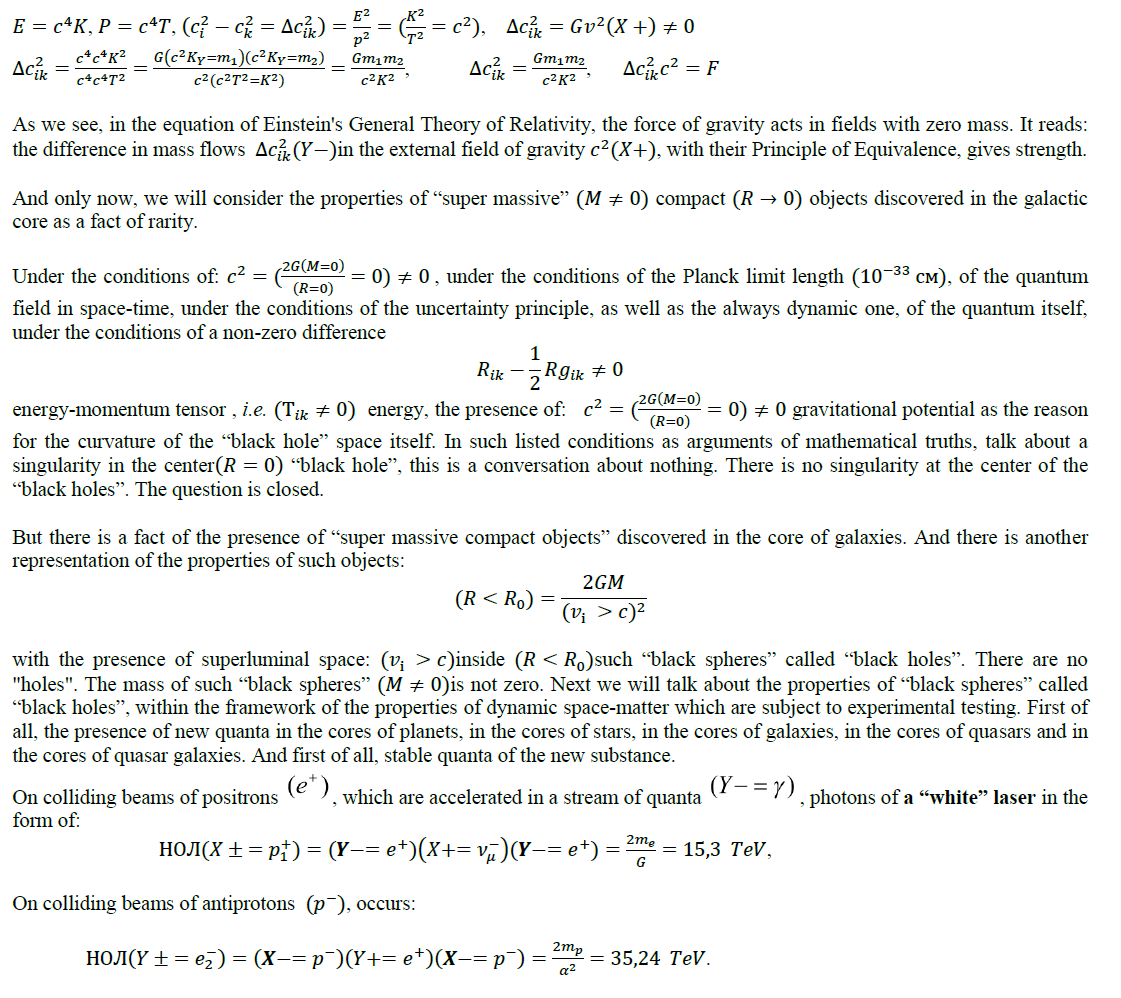
indivisible and stable quanta of matter, similar to the substance of electron quanta.

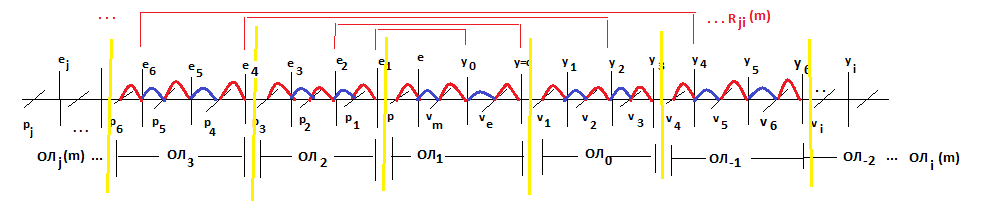
We are talking about a quantum coordinate system O_JI(m-n)in the space-matter of the Universe, in each O_JIlevel O_JIthere are three (X-=YX+)charge and two (Y-=X+)mass isopotentials. And in this quantum coordinate system, “heavy ”(pi/ji) quanta, each of which has its own “depth” of energy levels(v1/yi) quanta of physical vacuum. Let's imagine them in the form of models such R^ji(m) Indivisible Regions of space - the matter of the Universe.

FIG. 7. Spectrum of indivisible quanta.

This is a certain sphere in space-matter, in the center of which are “heavy”((pi/ji)) quanta that determine “down” and “up” along the radius, up to the level(v1/yi) quanta of the physical vacuum of space-matter of the Universe, for any similar object within this sphere.

In the axioms of dynamic space-matter, HOJi=KEM1 , we obtain for the masses (M) of indivisible quanta in (OJI_ji) levels:

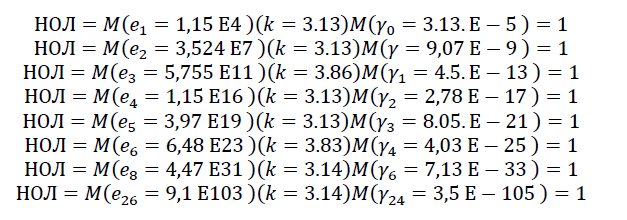
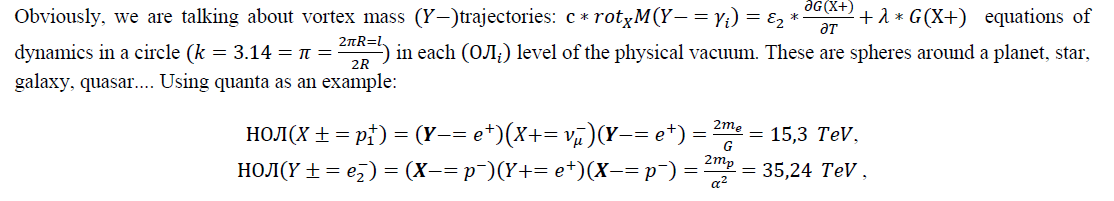
Conclusion

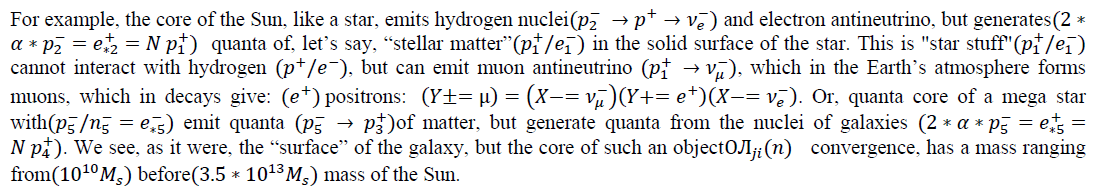
We are talking about valid objects OJI_ji(n) convergence, in the dynamic space-matter of the Universe. In this case, the calculated cause-and-effect relationships are indicated.

References

1. Skenderis K, Taylor M. The fuzzball proposal for black holes. Phys Reports. 2008;467(4-5):117-171.

   [Crossref] [Google Scholar]

2. Alexander DM, Hickox RC. What drives the growth of black holes? New Astron Rev. 2012;56(4):93-121.

   [Crossref] [Google Scholar]

3. Taylor EF, Wheeler JA. Exploring black holes. San Francisco: Addison Wesley Longman, 2000.
4. Novikov ID, Frolov VALERYP. Physics of black holes. Springer Science & Business Media, 2013.

   [Google Scholar]

5. Hawking SW. Black holes and thermodynamics. Phys Rev D. 1976;13(2):191.

   [Crossref] [Google Scholar]

6. Bekenstein JD. Black holes and the second law. In JACOB BEKENSTEIN: The Conservative Revolutionary, 2020:303-306.

   [Crossref] [Google Scholar]