Original Article
, Volume: 6( 3)Designing Force Field Engines
- *Correspondence:
- Solomon BT, Xodus One Foundation, 815 N Sherman Street, Denver, Colorado, USA, Tel: 310- 666-3553; E-mail: bts@XodusOneFoundation.org
Received: September 11, 2017; Accepted: October 20, 2017; Published: October 24, 2017
Citation: Solomon BT. Designing Force Field Engines. J Space Explor. 2017;6(3):132.
Abstract
The main objective of this paper is to present sample conceptual propulsion engines that researchers can tinker with to gain a better engineering understanding of how to research propulsion that is based on gravity modification.
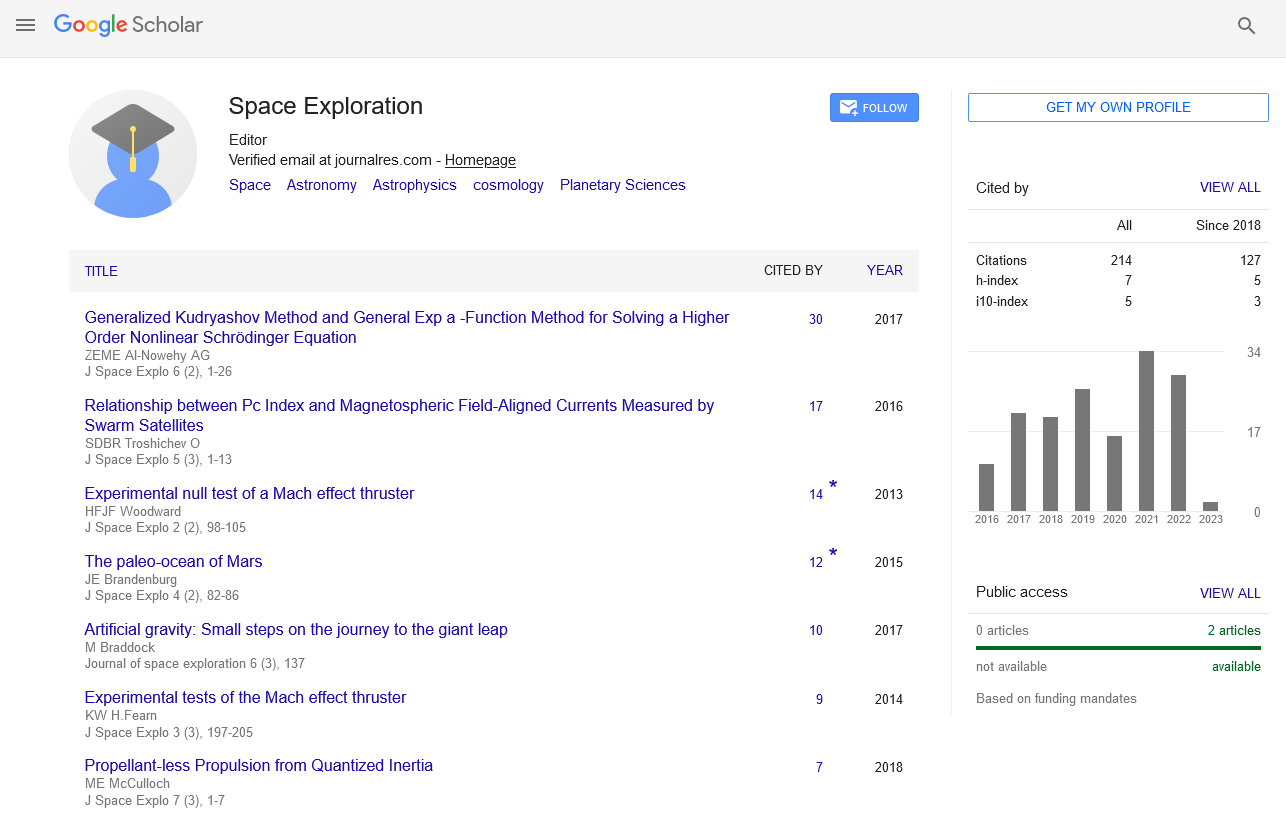
A Non- Inertia (Ni) Field is the spatial gradient of real or latent velocities. These velocities are real in mechanical structures, and latent in gravitational and electromagnetic field. These velocities have corresponding time dilations, and thus g=τc2 is the mathematical formula to calculate acceleration. It was verified that gravitational, electromagnetic and mechanical accelerations are present when a Ni Field is present. For example, a gravitational field is a spatial gradient of latent velocities along the field’s radii. g=τc2 is the mathematical expression of Hooft’s assertion that “absence of matter no longer guarantees local flatness”, and the new gravity modification based propulsion equation for force field engines.
To achieve Force Field based propulsion, a discussion of the latest findings with the problems in theoretical physics and warp drives is presented. Solomon showed that four criteria need to be present when designing force field engines (i) the spatial gradient of velocities, (ii) asymmetrical non-cancelling fields, (iii) vectoring, or the ability to change field direction and (iv) modulation, the ability to alter the field strength. The importance of Podkletnov’s gravity modification experiments is that they can lead to the confirmation that mass does not cause gravitational fields and therefore, matter and not mass is the cause of gravitational fields.
Two examples on how to construct Ni Field engines are presented. First, the Gravitational Column Launch, using Podkletnov-type devices to reverse the gravitational field above a launch vehicle and propel it into space. Second, the Unibeam Projector, a topological modification of Podkletnov’s spinning superconducting disc, to create spacecraft artificial gravity, and tractor beams.
Keywords
Alcubierre; Gravity; Electromagnetic force; Lorentz-Fitzgerald transformation; Electric fields; Gravity modification; Ni fields
Introduction
The purpose of this section is to provide a background as to why gravity modification is feasible. In 2015, Steinhardt [1] stated that the Planck Space Telescope data shows that the Universe is simpler than had been thought for three reasons (1)
The deviations in the Cosmic Microwave Background is within the limits of quantum theory, (2) Don’t see gravitation waves i.e., inflation and (3) Don’t see the effects of strings theories. Esftathiou [1] concurred, adding that theories leading to infinities reflects a crisis in physics and a resolution to these problems would involve revolutionary physics. In 2012 using NASA’s Fermi Gamma-Ray Space Telescope photographs of gamma ray burst, Nemiroff [2] showed that quantum foam could not exist.
In 2013 Solomon [3] proposed that both exotic matter and strings could not exist. First, the former leads to perpetual motion machine, and the latter contradicts Lorentz-FitzGerald Transformations (LFT). By assuming that particles were compressive Solomon [3-8] proposed a new equation for gravitational acceleration (1) without a priori knowledge of mass and radius of the gravitating object.
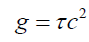 (1)
(1)
Where τ is the spatial gradient of the time dilation transformation or change in time dilation transformation divided by that distance, and noting that the time dilation transformation is the ratio of tv/t0 per Lorentz-FitzGerald Transformations (LFT) or (2), and Newtonian Transformations (3). Table 1. [7-9] presents the comparisons for gravitational acceleration using Newtonian physics and (1).
| Heavenly Body |
Gravitational g=GM/R2 (m/s2) |
Acceleration g=τc2 (m/s2) |
Error in g PPM (Parts Per Million) |
Change in Time Dilation Transformation Across Particle |
Gravitationally Distorted Distance (m) |
|---|---|---|---|---|---|
| Earth | 9.802893102465580 | 9.802893122930450 | -0.002087636085405 | 1.090173598033850E-27 | 9.994999993044690E-12 |
| Jupiter | 24.868616073880500 | 24.868617547825600 | -0.059269286588270 | 2.765623312782150E-27 | 9.994999802534500E-12 |
| Mars | 3.820506452258500 | 3.820506453910170 | -0.000432315179401 | 4.248761276124040E-28 | 9.994999998559660E-12 |
| Mercury | 4.023548458075780 | 4.023548459394310 | -0.000327701863842 | 4.474563017681310E-28 | 9.994999998908200E-12 |
| Neptune | 11.265170220787000 | 11.265170325416100 | -0.009287836549597 | 1.252792525904500E-27 | 9.994999969056020E-12 |
| Pluto | 0.605452400756143 | 0.605452400770215 | -0.000023241154340 | 6.733198193257340E-29 | 9.994999999922560E-12 |
| Saturn | 10.563045030532200 | 10.563045253624700 | -0.021120092215353 | 1.174709632439570E-27 | 9.994999929634890E-12 |
| Sun | 280.302037387103000 | 280.303846992092000 | -6.455910938663970 | 3.117234802040310E-26 | 9.994978491149290E-12 |
| Uranus | 8.758854078032970 | 8.758854143845340 | -0.007513810986813 | 9.740666759941420E-28 | 9.994999974966480E-12 |
| Venus | 8.873871553457870 | 8.873871569412800 | -0.001797966844070 | 9.868576936355740E-28 | 9.994999994009770E-12 |
Notes: (a) Though the data presented is only to 15 decimal places, all numerical analyses were conducted to 250 significant digits using G of 6.67259x10-11. (b) The numerical results validate equation (1), that gravitational acceleration can be derived without reference to its mass source as the errors between Newtonian g (column 2) and Ni Field g (column 3) is < |6.5| ppm, (c) Combining all recent experimental results [4] provides measured range of between 6.671x10-11 to 6.676x10-11 or a mean of 6.6738x10-11 and standard deviation of 0.0012x10-11 that the true G is in this range. (d) These near field gravity probe G measurements are a good example of precision versus accuracy and proof of the presence of systematic errors.
Source: Papers [7-9]
Table 1: Gravitational acceleration values using Newtonian equation and equation (15), for a particle diameter of 10-11 m.
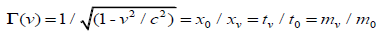 (2)
(2)
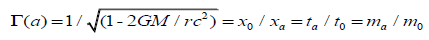 (3)
(3)
Therefore, an expanded scope of new gravitational theories requires applicability in (1) distant cosmology, (2) near field local gravity probes, and (3) local gravity modification, thereby introducing more avenues for exploration. Near field gravity probe research [10-13] has proved that it is very difficult to concur on a specific value for the gravitational constant G. This points to the need for a different model for gravitation.
What if gravity is not caused by mass? Podkletnov [14,15] reported gravity shielding effects above a spinning superconducting ceramic disc. Podkletnov’s results have not been reproduced. However, other researchers’ [16,17] ceramic discs cracked before reaching Podkletnov’s disc spin requirements. Solomon [7,9] deconstructed Podkletnov’s experiments so that future experimenters can avoid the mistakes of past experiments [16-17]. If gravity modification experiments are vindicated they confirm that gravitational fields are not caused by mass but by some other property of matter that can be measured equivalent to mass.
Solomon [8] proposed a schema approach to understanding gravity. A schema is an outline of a model of a complex reality to assist in explaining this reality. The work of various researchers [7,8,18] in the gravity field can be presented by a conceptual formalism referred to as source-field-effect schema. The source-field-effect schema corresponds to the mass-gravityacceleration phenomenon, respectively.
Solomon proposed [3,5-8] that in contemporary physics, there are three types of schema with their corresponding particle characteristics, (i) General Relativity as a geometric surface schema and ignores particle characteristics, (ii) Quantum Mechanics with inelastic point-like elementary particle schema, and (iii) String Theories with tensile strings schema. Solomon [7,8] proposed a fourth schema that is consistent with General Relativity, with compressive particles [19].
Solomon [20] and Solomon and Beckwith [21] proposed that this quark interaction is the source of gravitational fields. The equivalent measure concept is described by mass as a proxy for number of quarks, and number of quarks as a proxy for quark interaction [22,23].
General Relativity [24] begins with separation vectors. This schema approach is presented by equations (4) to (8). The standard z-direction (4) separation vector is a function of gravitational mass m, and gravitational constant G at a distance r from the source. Gravitational acceleration g (5) is defined by these separation vectors. This three-part schema can be described as, i) the mass source (8), ii) the field (7), and iii) the field effect or acceleration (5).
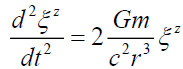 (4)
(4)
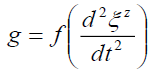 (5)
(5)
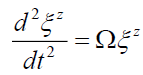 (6)
(6)
or,
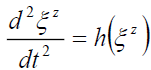 (7)
(7)
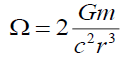 (8)
(8)
The importance of the shape of spacetime, unlike Newtonian gravity or General Relativity [24], is that it informs what the spatial gradients of time dilation, mass increase and length contraction are. General Relativity [24] theorizes gravity as the curving of spacetime, shape change, to cause this effect of gravity. Similarly, one could propose for a non-point sized particle, the shape change of spacetime in the local region of the particle is mirrored by an identical shape change of the particle. This is not macro body deformation due to the gravitational gradienti but particle-level deformation due to space contraction, time dilation and mass increase. The resulting deformation of the particle’s shape is evidenced as a shift in the center of fields of its mass-volume ‘field’; and is a logical extension of the inertia Lorentz-Fitzgerald transformations Γ(v) (2) and the Newtonian non-inertia gravitational field transformation Γ(a) (3). In the generic form, the environmental transformation Γ(e),
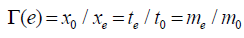 (9)
(9)
Solomon [3,5-8] proposed that this mass-volume field deformation was due to the internal effects of the Newtonian noninertia transformations Γ(a), present in the local region of the external gravitational field such that the spacetime transformations Γs(x,y,z,t) are concurrently reflected as particle transformations Γp(x,y,z,t) or,
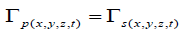 (10)
(10)
The utility of (10) is that it explains why the gravitational field passes through all matter. Further, using the Newtonian noninertia transformations Γ(a) one can now replace the right-hand side separation vector function in equation (5) with mass and volume spatial gradients per equation (11).
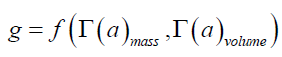 (11)
(11)
In 2015 Solomon [25] proposed a 4th approach to forces not related to Relativity, String or Quantum (RSQ) theories. That a particle’s velocity and acceleration is evidenced by the shift in the Center of Field CF of the local field’s spatial gradient. This field could be gravitational, electromagnetic, electric, magnetic or mechanical motion. It was proposed that the shift in the Center of Field CF, is the result of the deformation of this field just as altering the shape of an object would alter its Center of Mass, CM. The magnitude and direction of this CF shift governs the strength and direction (attraction or repulsion) of motion. Using the Center of Mass concept, the Center of Field CF of a field F that ranges from lower limit L to upper limit U, is defined as:
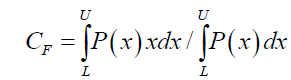 (12)
(12)
Where P is the property of the Field used to evaluate the Field’s CF. The relevant field property depends upon the type of deformation applied to this field. If the deformation of the field property is non-linear then the spatial gradient of the Field’s property P or dP/dx is the parameter used to estimate the Field’s CF. If the deformation of the field property is linear than then the field’s property P is the parameter used to estimate the Field’s CF as the spatial gradient of P is zero. The importance of this finding is that Poincaré stresses [26] no longer exists as electric field lines are no longer repulsive. This led to the simplification of particle structure, and Solomon proposed (i) a new model for the nuclei [27] that eliminates the need for a particle based approach to weak and strong forces, (ii) a new model for the electron shell [28], (iii) a replacement for the Schrödinger wave function [29-31], and (iv) a new structured approach to particle design [28] that could possibly replace the Standard Model, though much work is required.
As a paper on force field engines, there is one last point, the Alcubierre warp drive [32] as a means to interstellar drive based on exotic matter. The two problems with the Alcubierre warp drive are exotic matter and axioms.
First, Solomon [3] showed that exotic cannot exist as it leads to perpetual motion machines. However, there is a subtler issue. The esteemed Bondi [19] authenticated exotic matter using General Relativity or rephrasing, General Relativity endorsed perpetual motion physics. The lesson here is care is required not to modify or develop a theory that leads to perpetual motion physics. As Klein [33] stated, mathematics has become so powerful that it can now be used to prove anything. Therefore, the urgent need for the extensive use of empirical data and process models to guide the mathematical development.
The second problem are the axioms. As pointed out earlier with Bondi’s exotic matter, General Relativity may not provide meaningful results in extreme conditions. Beckwith [33] states that “in assuming violation of conservation of energy, within the confines of a local universe, as modeled either by steady state models, or the usual FRW universe structure, one is by necessity appealing to a multiverse structure, i.e., multiple universes. However, unless one explicitly models the evolutionary history of the universe, used by the Alcubierre drive, as a multiverse, one is using a single universe, but implicitly assuming a physical process which could only work if a multiverse structure exists. Hence, the Alcubierre drive program, modeled within a single universe, is appealing to a multiverse structure in order to allow for its local universe violation of conservation of energy to occur. By any physical reasoning, the result is a reduc to absurdum which is not supported by logic” [34,35].
Experimental Evidence
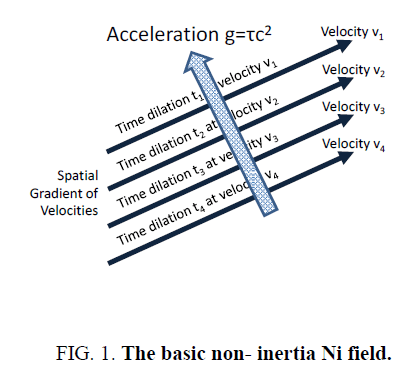
The purpose of this section is to provide a background as how gravity modification is feasible. Per Solomon [7,8,36] a gravitational field is a spatial gradient of tangential latent velocities along the axis of any radii and exhibits an acceleration along that radius. Therefore, the Non- Inertia or Ni field is defined as a field that exhibits acceleration along a spatial gradient of latent or real velocities. Figure 1. [7,9] illustrates the Ni field of four velocity vectors v1, v2, v3 and v4 and their associated time dilations.
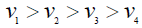 (13)
(13)
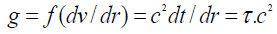 (14)
(14)
In effect, a Ni Field is a force field as it is a field that occupies space which is accompanied by an acceleration vector. Solomon [7,9,32] proposed that for a force field to be technologically useful it has two properties, field modulation and field vectoring. Field modulation is the ability to attenuate (shield) or amplify (intensify) the field strength. Second, field vectoring is the ability to change the direction of force. Both properties exist in Nature, field modulation is determined by the mass and radius of the heavenly body, and field vectoring changes with relative position of this heavenly body.
The Ni Field method (Table 2) [7-9], is in good agreement with both classical mechanics and classical electromagnetism. However, there is one more test for the Ni Field method. Can the Ni Field method solve a problem that classical mechanics cannot? Laithwaite [37,38] had demonstrated that a spinning disc (spin radius) when rotated about himself (rotational radius) would lose weight. To date nobody, using classical mechanics, has been able to derive a solution to this Laithwaite Big Wheel enigma that matches the experimental results.
| Acceleration | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Angular Velocity |
Path Radius (m) |
Tangential Velocity (m/s) |
Particle Size (m) |
Centripetal Method | Electro- Magnetic Theory |
Mechanical Ni Field Method | Mechanical Ni Field Error |
Electromagnetic Ni Field Method | Electro-magnetic Ni Field Error |
| Equation (16) | Equation (15) | Equations (1) | (1)-(16) | Using Eqn. (1) | (1)-(15) | ||||
| 68 | 9.85 | 669.8 | 1.00E-30 | 45,546.40 | 45,546.40 | 45,546.40 | 2.4033E-13 | 45,546.4000003409 | -3.4E-07 |
| 127 | 4.07 | 516.89 | 1.00E-27 | 65,645.03 | 65,645.03 | 65,645.03 | 4.1720E-14 | 65,645.0300002925 | -2.9E-07 |
| 49 | 5.01 | 245.49 | 1.00E-24 | 12,029.01 | 12,029.01 | 12,029.01 | 3.2700E-15 | 12,029.0100000120 | -1.2E-08 |
| 98 | 6.13 | 600.74 | 1.00E-21 | 58,872.52 | 58,872.52 | 58,872.52 | 6.0000E-16 | 58,872.5200003546 | -3.5E-07 |
| 148 | 4.75 | 703 | 1.00E-18 | 104,044.00 | 104,044.00 | 104,044.00 | 1.7090E-12 | 104,044.000000858 | -8.6E-07 |
| 116 | 0.42 | 48.72 | 1.00E-15 | 5,651.52 | 5,651.52 | 5,651.52 | 9.6100E-15 | 5,651.5200000002 | -2.2E-10 |
| 96 | 0.79 | 75.84 | 1.00E-12 | 7,280.64 | 7,280.64 | 7,280.64 | 3.3797E-12 | 7,280.6400000007 | -6.8E-10 |
| 2 | 1.17 | 2.34 | 1.00E-09 | 4.68 | 4.68 | 4.68 | 6.0083E-12 | 4.6800000000 | -5.1E-14 |
| 74 | 1.86 | 137.64 | 1.00E-06 | 10,185.36 | 10,185.36 | 10,185.36 | 2.1640E-14 | 10,185.3600000812 | -8.1E-08 |
| 170 | 4.64 | 788.8 | 1.00E-03 | 134,096.00 | 134,096.00 | 134,096.00 | 7.4337E-13 | 134,096.000413369 | -4.1E-04 |
Note: The new Ni field method agrees with other methods except in the last row where particle size is >10-3 m. This is because the distance between the two velocities is great enough to be the effective or averaged acceleration over a large distance.
Table 2: The Ni field method is in good agreement with both classical mechanics and classical electromagnetism.
Solomon investigated this [7-9]. The results confirm Laithwaite’s [9,37,38] original demonstration that a disc spinning at 5,000rpm and rotating at 7 rpm, with a radius of rotation of at least 1m, and spin radius of 0.3m would be almost weightless (9.8 m/s2 - 9.7 m/s2 = 0.1 m/s2), if not rise. (15) presents the findings. The acceleration a created by a rotating-spinning disc’s three-dimensional Ni Field with spin ωs, disc radius s, rotational ωd, rotation radius d and hypotenuse h formed by s and d is given by:
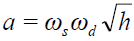
Though Laithwaite demonstrated weight loss, this is a weight change phenomenon as both weight loss and gain are observed. If the sense of the spin and rotation are different, the direction of the acceleration is reversed, as one of the ω’s is negative.
Hayasaka and Takeuchi [39] had reported that a gyroscope would lose weight, but Lou et al. [40] could not reproduce this effect. Given their experiments downward pointing spin vector, eq. (15) shows that Lou et al. were correct because eq. (15) requires that acceleration produced be orthogonal to both spin and rotation. Therefore, for weight change to be observed, the spin vector should be orthogonal to the gravitational field, and spin vector needs to be rotated in a manner that is orthogonal to the spin plane. Thus, confirming, that the Ω function (8) can be replaced by purely mechanical functions.
Some significant inferences are,
• A mathematical property is now explained by a physical process: The cross product (16) in electromagnetic theory, Solomon [7-9], is due to the spherical shape of the electron’s field and causes an acceleration that is orthogonal to its velocity and the magnetic field lines.
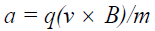 (15)
(15)
• The Ω function (8) can be replaced with an electromagnetic function: Table 2 confirms this as both the classical methods and the Ni Field methods agree with each other for gravitational, mechanical and electromagnetic accelerations.
• Ni Field Unification: Table 2. shows that the Ni Field method provides an elegantly simple unification of macro forces by the common equation (14).
• Ni Field subset: (15) suggests that classical mechanics is a subset of the Ni Field method, but more research is required to get there.
Lessons from Podkletnov Experiments
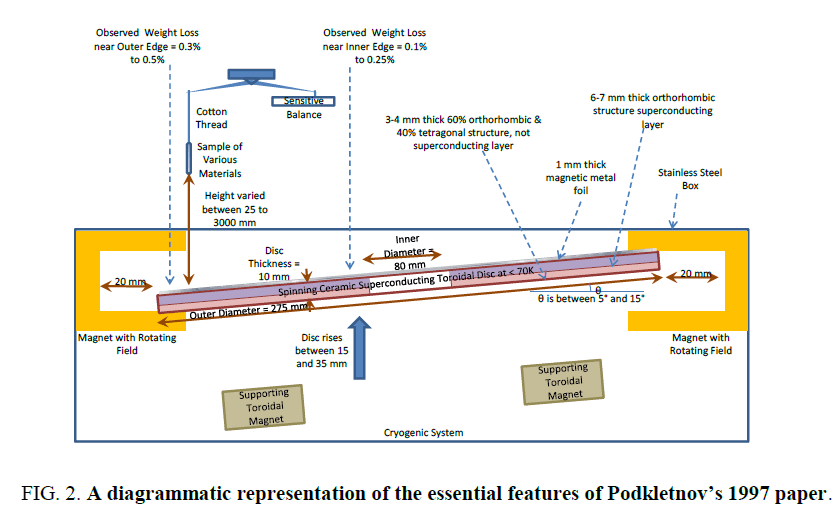
The purpose of this section is to provide a brief understanding of why and how Podkletnov’s [14,15] design works. The importance of Podkletnov [14,15] experiments is that if correctly reproduced it confirms that gravity is not caused by mass but by some other constituent of matter. Podkletnov [14,15] reported that an electrified superconducting ceramic disc (see Figure 2. [7,9]) at temperatures below TC (critical temperature) would exhibit gravity shielding effects above the disc when this disc was spun to 5,000 rpm.
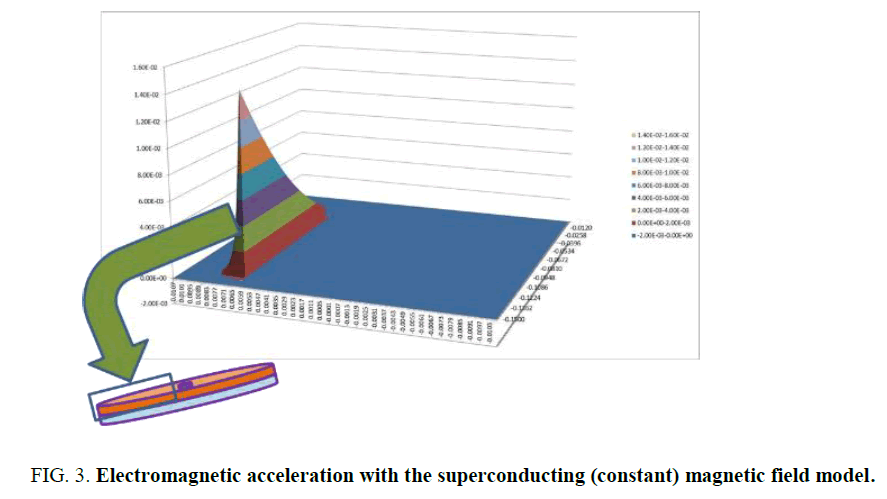
Solomon [7,9] reviewed Podkletnov’s [14,15] papers using the source-field-effect schema, and proposed that any hypothesis on superconducting gravity shielding should explain four observations, the stationary disc weight loss, spinning disc weight loss, weight loss increases along a radial distance and weight increase. Its importance to force field engine design is field modulation and field vectoring, i.e., gravitational field strength modulation, either attenuation (shielding) or amplification (intensification) and gravitational field vectoring, or a directed force field, the use of fields to change the direction of force. Solomon [7,9] using an approximate numerical model for this superconducting ceramic disc, showed that the shielding effect indeed increases with radius from inner to the outer radius (Figure 3.)[7,9].
Note that the top side had overlapping electric and magnetic fields while the bottom side did not as the bottom side of this ceramic disc was not superconducting. By the Ni Field method [7,9] the top side of the spinning disc had an upward acceleration that negated gravity. The latent velocity of the electrified superconducting magnetic field should have a latent velocity vhigh at higher part of the field that is greater than the latent velocity vlow at the lower part of the field.
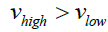 (16)
(16)
This occurs when their respective high and low parameters (electric field strength E, magnetic field strength B and height above disc d) along an electric field line obey,
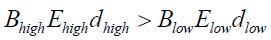 (17)
(17)
As the bottom side did not have overlapping magnetic and electric fields, this would not apply. If it did then the symmetrical structure would cancel any force field effects. Therefore, the electric/magnetic field effects were asymmetrical, with an effect on the top side and none on the bottom side.
Similar asymmetry is observed in a gravitational field. Particles deform asymmetrically [3-8] and a particle’s, near side (of the gravitational source) is flatter and denser than the far side. Likewise, with mechanical and electromagnetic forces. Solomon [24] also showed that this asymmetrical field effect is present with charged particles, and thus magnetic monopoles.
Force Field Design Rules
From the above discussion, to build a force field engine, one has to create a Ni Field that obeys four design rules. These rules are:
• The field effects must result in a spatial gradient of latent or real velocities. These velocities are latent with gravitational and electromagnetic fields, and real with mechanical structures such as centripetal motion and Laithewaite’s Big Wheel experiment.
• The field must be asymmetrical, and non-cancelling. This is observed in the asymmetrical ovoid-like [7,9] shape of particles in gravitational fields. In the Podkletnov experiments [7,9] this is achieved by the asymmetrical structure of the electrified magnetic field. Note that there are no net forces in charged particles and naturally occurring magnetic fields as these fields are symmetrical.
• Vectoring is provided by direction of the spatial gradient of velocities. In gravitational fields, this vectoring is along the radii of the field. In the electron moving in a magnetic field, this vectoring is derived from the direction of the magnetic field acting on the spherical shape of the electron’s electric field.
• Modulation is provided by the field strengths. In gravitational fields modulation is accomplished by the amount of matter, with mass as a proxy for this quantity of matter [20] and by the radius of the gravitating source. In the electron moving in a magnetic field, this modulation is derived from the magnetic field strength.
Engine Concepts
Using Ni Fields two engine concepts are proposed to facilitate an understanding of how Ni Fields can be implemented. The first is the Gravitational Column Launch, GCL [41]. By equations (17) and (18) a superconducting magnetic field is not required [7,9]. Knowing that gravity shielding was observed above Podkletnov’s device, therefore anything above this device would lose weight. Using non-superconducting magnetic fields, a square matrix of 1,000 × 1,000 of these devices several meters under the launch pad, one could generate a gravitationally modified launch column. This would impell the space vehicle into outer space. To recover the vehicle, the spacecraft simply “docks” into the GCL which then gently retracts the spacecraft.
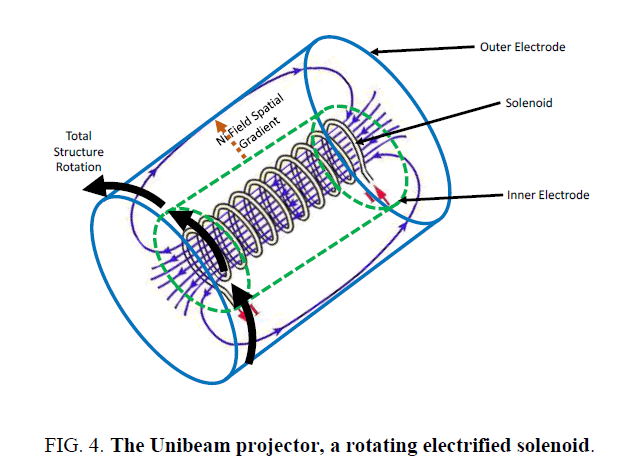
The second concept is the Unibeam Projector. It is a topological modification of Podkletnov’s spinning superconducting disc (Figure 4). By equations (17) and (18) superconducting magnetic field is not required [7,9], therefore, a Ni Field can be created by spinning a magnetic solenoid enclosed by an orthogonal electric field. The spatial gradient of the Ni Field will be along the radii orthogonal to cylinder, from the center of the solenoid to the outer electric field electrodes. If the outer electrodes are formed by sectional strips, then by turning on selected strips synchronized to the rotation one should be able to create a unidirectional Ni Field or a tractor beam or a means to spaceship artificial gravity [42]. Vectoring is achieved by changing the synchronized electrified sectional strip. Modulation is achieved by power to the solenoid. If the net high velocity, tangential rotational velocity vr,high + latent electromagnetic velocity, vhigh near the outer electrode is greater than the net low velocity, tangential rotational velocity vr,low + latent electromagnetic velocity, vlow near the inner electrode (31) than the acceleration is outward or repulsive, else it is inward and attractive.
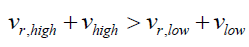 (18)
(18)
Conclusion
This paper presented an approach to determining how force fields can be generated, partly by showing what is no longer correct, and partly by proposing new empirically consistent concepts. Given that Relativity, String & Quantum (RSQ) theories can be replaced by Spatial Gradients as the mechanism for force, Ni Fields are the future of propulsion engineering. Two engine concepts that are relatively easy for experiments to conduct have been proposed.
Acknowledgements
I would like to thank Dr, Andrew Beckwith, for his review, comments, advice and suggestions, especially with respect to the Alcubierre drive, on how to improve this paper.
References
- Efstathiou G, Pryke C, Steinhardt P, et al. Spotlight live: Looking back in time-oldest light in existence offers insight into the universe. The Kavli Foundation; 2015.
- Nemiroff R. Bounds on spectral dispersion from fermi-detected gamma ray bursts. Phys Rev Lett. 2012;108:231103.
- Solomon BT. New evidence, conditions, instruments and experiments for gravitational theories. J Modern Phys. 2013;8A.
- Cowen R. Quantum method closes in on gravitational constant: Cold rubidium atoms provide fresh approach to measuring Newton's big G. Nature News; 2014.
- Solomon BT. Empirical evidence suggests a need for a different gravitational theory. In: The proceedings of the 100 Year Starship Study Public Symposium (100YSS,); 2013.
- Solomon BT. Empirical evidence suggest a need for a different gravitational theory, American Physical Society (APS) April Conference, Denver; 2013.
- Solomon BT. An introduction to gravity modification: A guide to using Laithwaite's and Podkletnov's experiments and the physics of forces for empirical results. 2nd edition. Universal Publishers, Boca Raton: 2012.
- Solomon BT. Gravitational acceleration without mass and non-inertia fields. Phys Essays. 2011;24: 327.
- Solomon BT. An approach to gravity modification as a propulsion technology. In: The proceedings of the space, propulsion and energy sciences International Forum (SPESIF-09). Glen AR, editors. AIP Conference Proceedings 1103; Melville, New York; 2009.
- Gundlach JH, Merkowitz SM. Measurement of Newton's constant using a torsion balance with angular acceleration feedback Phys Rev Lett. 2000;852869.
- Parks HV, Faller JE. A simple pendulum determination of the gravitational constant. Phys Rev Lett. 2010; 105:110801.
- Luo J, Liu Q, Liang-Cheng Tu, et al. Determination of the Newtonian gravitational constant G with time-of-swing method. Phys Rev Lett. 2009;102:240801.
- Schlamminger E, Holzschuh W, Kündig D, et al. Measurement of Newton’s gravitational constant. Phys Rev D. 2006;74:082001.
- Podkletnov E. Weak gravitational shielding properties of composite bulk YBa2Cu3O7-x superconductor below 70K under em field. lanl.gov; 1997.
- Podkletnov E, Nieminen R. A possibility of gravitational force shielding by bulk YBa2Cu3O7-x superconductor. Physica C. 1992;203:441-44.
- Woods RC, Cooke SG, Helme J, et al. Gravity modification by high-temperature superconductors. In: The proceedings of the 37th AIAA/ASME/SAE/ASSEE Joint Propulsion Conference & Exhibit, 8-11 July, Salt Lake City, Utah; 2001.
- Hathaway G, Cleveland B, Bao Y, et al. Gravity Modification Experiments Using a Rotating Superconducting Disk and Radio Frequency Fields. Physica C. 2013;385(4):488-500.
- Amoroso RL, Hunter G, Kafatos M et al. Gravitation and cosmology: From the hubble radius to the plank scale. Proceedings of a Symposium in Honour of the 80th Birthday of Jean-Pierre Vigier, Kluwer Academic Publishers, Boston, USA; 2002.
- Bondi H. Negative mass in general relativity. Rev Mod Phys. 1957;29:423.
- Solomon BT. The variable isotopic gravitational constant, super physics for super technologies: Replacing Bohr, Heisenberg, Schrodinger & Einstein, Propulsion Physics Inc Denver; 2015.
- Solomon BT, Beckwith AW. The origins of gravitational fields. J Space Explor. 2017;6(1):111.
- Hooft G. The Mathematical basis for deterministic quantum mechanics. Found Phys. 2008;38:733.
- Wagoner RV. 26th SLAC Summer Institute on Particle Physics. 1998;1:SSI98.
- Misner CW, Thorne KS, Wheeler JA. Gravitation. W.H. Freeman and Company, New York, NY, USA, 1973.
- Solomon BT. A universal approach to forces, super physics for super technologies: Replacing Bohr, Heisenberg, Schrodinger & Einstein. Propulsion Physics Inc; 2015.
- Feynman R. Feynman Lectures on Physics. Chapters 28-34.
- Solomon BT. A non standard model nucleon/nuclei structure, super physics for super technologies: Replacing Bohr, Heisenberg, Schrodinger & Einstein, Propulsion Physics Inc; 2015.
- Solomon BT. Replacing Schrödinger, Super Physics for Super Technologies: Replacing Bohr, Heisenberg, Schrodinger & Einstein, Propulsion Physics Inc. 2015.
- Solomon BT, Beckwith AW. Photon probability control with experiments. J Space Explor. 2017;6(1):116.
- Solomon BT, Beckwith AW. Probability, randomness & subspace, with experiments. J Space Explor. 2017;6(1):110.
- Solomon AW. Beckwith probability as a field theory.
- Solomon BT. Particle structure, super physics for super technologies: Replacing Bohr, Heisenberg, Schrodinger & Einstein, Propulsion Physics Inc; 2015.
- Torchinsky J. The painful truth about NASA's warp drive spaceship from a physicist. Jalopnik; 2014.
- Klein M. Mathematics: The loss of certainty. Oxford University Press; 1982.
- Beckwith A. A conversation with the Professor, Department of Physics, Chongqing University, China.
- Solomon BT. Reverse Engineering Podkletnov’s Experiments. In: The proceedings of the Space, Propulsion & Energy Sciences International Forum (SPESIF-11), Edited by Robertson GA, Physics Procedia, Elsevier Science; 2011.
- http://www.gyroscopes.org/heretic.asp.
- Laithwaite E. Royal Institution’s 1974-1975 Christmas Lectures, presented at The Royal Institution, United Kingdom; 1974.
- Hideo H, Sakae T. Anomalous weight reduction on a Gyroscope’s right rotations around the vertical axis on the earth. Phys Rev Lett. 1989;63(25): 2701-04.
- Luo J, Nie YX, Zhang YZ, et al. Null result for violation of the equivalence principle with free-fall rotating gyroscopes. Phys Rev D. 2002;65;042005.
- Solomon BT. Building gravitational column launch engines. Xodus One Foundation; 2015.
- Solomon BT. Non-Gaussian photon probability distributions, in the proceedings of the space, propulsion and energy sciences International Forum (SPESIF-10). Glen AR, editor. AIP Conference Proceedings 1208; Melville, New York; 2010.