Review
, Volume: 6( 2)A New Splitting Method for the Navier-Stokes Equation
- *Correspondence:
- Amattouch MR , Department of Mathematics, Faculty of Sciences and Techniques, University of Abdelmalek Essaadi, BP.416, Tangier, Morocco, Tel: +212 5399-79095; E-mail: amattouch36@yhoo.fr
Received: July 17, 2017; Accepted: August 22, 2017; Published: August 26, 2017
Citation:Amattouch MR, Nagid N, Belhadj H. A New Splitting Method for the Navier-Stokes Equation. J Space Explor. 2017;6(2):127
Abstract
This work is devoted to a robust splitting method applied to solve the time dependent incompressible Navier-Stokes equation. The proposed method is based on analytical step of computing and a vortex method easy to handle to compute the velocities and a Poisson equation to compute the pressure. The Poisson equation is solved by an optimized domain decomposition method. Several test-cases of analytical problems illustrate this approach and show the efficiency of the proposed new method
Keywords
Navier-Stokes equation; Splitting operator; Vortex method; Optimized domain decomposition
Introduction
The aim of this paper is to propose a new splitting operator to solve a non-linear incompressible Navier-Stokes equation on a bounded domain such that:
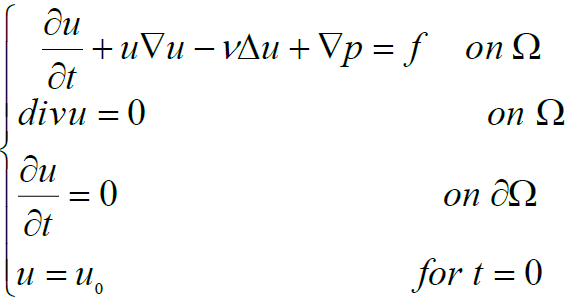 (1)
(1)
a condition on pressure to have the uniqueness of the problem.
Applications in engineering and aerodynamics often result in models consisting of large systems of these equations. For example, direct turbulent flow simulations (DNS) need to solve large Navier-Stokes equations. Due to the size of the model, the usage of direct, well-known approximation methods like finite element is not feasible and one needs to partition or split the problem.
There are many splitting operators in the Navier-Stokes jargon; we can cite the Chorin's projection scheme, the Van Kan's projection scheme and the Glowinski's splitting scheme. Of course, there are other splitting method more accurate [1-5] but here we study a splitting method that transform the Navier-Stokes equation on easy equations to solve and implement in software. The equation contains a non-linear term which is not symmetric and heavy to resolve in time with an implicit scheme, an explicit scheme is often inaccurate. So, the proposed splitting method resolve this problem by using an analytical solution to the non-linear and the viscous term of the equation. Then we obtain an equation of pressure and velocity that we separate in a Poisson equation in space and an equation easy to solve by the vortex method [6,7]. To make the method quick, we propose a new domain decomposition method to solve the Poisson equation. This method is based on a transmission condition of fractional derivative in the interface between sub-domains which converges in two iterations.
At the end of this work you can find some numerical experiment compared to analytical solution that effectively illustrate the efficiency of our proposed methods.
The Splitting Method
In this section, we present the splitting method for the equation (1) where we decouple u and p and separate convection diffusion term from incompressibility:
Let N a positive integer, 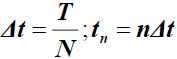 with n=0, 1 ..., N be a uniform partition of the time period [0, T].
with n=0, 1 ..., N be a uniform partition of the time period [0, T].
We consider intermediate times 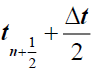
We take in the beginning U0=u0 and concede the two steps:
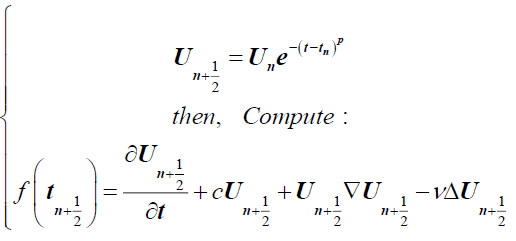 (2)
(2)
Then we solve,
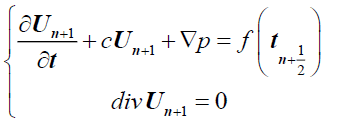 (3)
(3)
By applying the divergence and the rotational, this equation is equivalent to the two next equations:
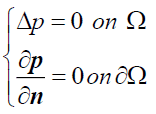 (4)
(4)
And
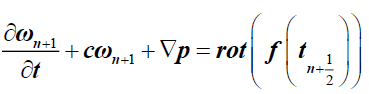 (5)
(5)
Where 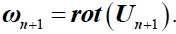 .
.
These two equations are solved by a discontinuous Galerkin method to ensure best regularity, accuracy and the continuity in thin meshes.
Notice that the equation (5) is a system of differentials equations that is easy to solve analytically.
Remarks
Replacing 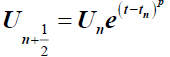 in (3) we obtain:
in (3) we obtain:
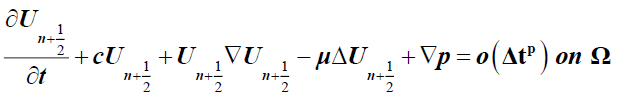 (6)
(6)
This result show that our method converges in p order per time.
In the case of a Dirichlet condition step 1 in equation (2) is replaced by:
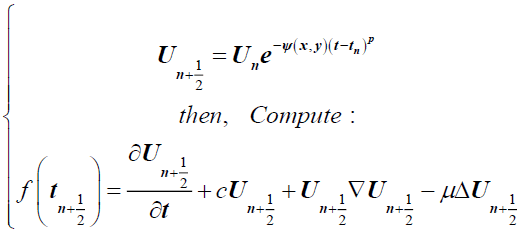 (7)
(7)
ψ is a function that verify 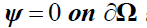 and: div ψ = 0 on Ω
and: div ψ = 0 on Ω
The Domain Decomposition Method
Domain decomposition methods consist of splitting initial problem into two or more sub-problems with smaller dimensions which make the computations fast. Many authors have studied domain decomposition methods these last decades [8,9]. Among these methods we consider in this work the method called second order optimized method OO2. This method was developed by different authors [10,11]. We present the OO2 method as in [10,11] applied to a reaction advection diffusion equation and then we will apply this method to the Poisson equation.
We split the domain Ω for example in two sub-domains Ω1 and Ω2 with an interface Γ (Figure. 1).
Then we built two sequences u1P and u2P respectively solutions of two sub-problems as described below:
We choose two initials functions u10 defined on Ω1 and u20 defined on Ω2 then we consider the two problems:
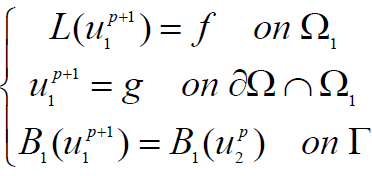 (8)
(8)
and
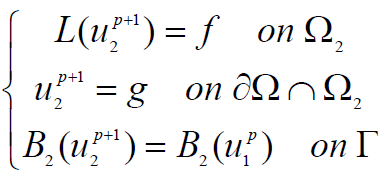 (9)
(9)
Where,
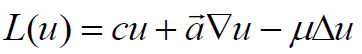 (10)
(10)
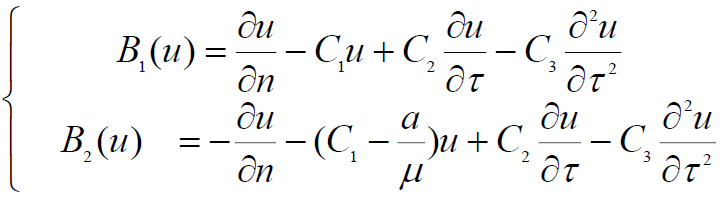 (11)
(11)
n and τ are the normal and the tangent on Ω1
Because of the Fourier analysis we show that the rate of convergence in the Fourier way is [6]:
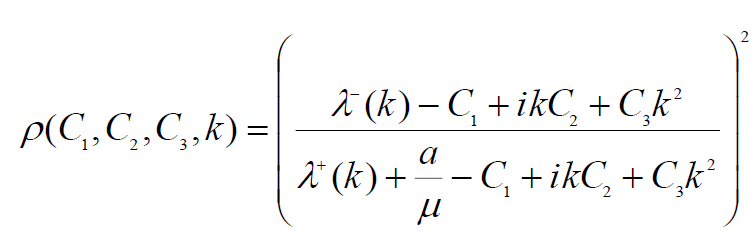 (12)
(12)
Where,
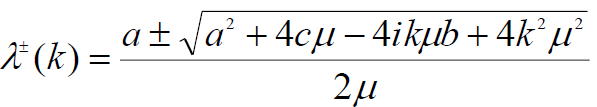 (13)
(13)
In order to optimize the method, we need to optimize the rate of convergence so we look for:
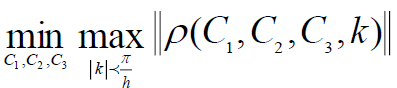
We prove that ([9]) if c>0 and sign(b)=sign(C2) and C3≥0 then,
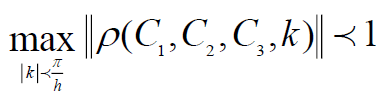
In our work, we treat a Poisson equation which mean c=0 and make the OO2 method not convergent. To avoid this issue, we propose a non-symmetric interface condition as follows which ensure two iterations convergence of our method: u10 defined on Ω1 then the first step is to solve:
Then we solve the next iteration:
 (14)
(14)
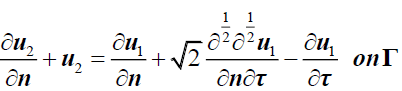
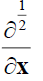 is the fractional Caputo derivative?
is the fractional Caputo derivative?
We used to prove that the rate of convergence is of two orders the Fourier transform using result:
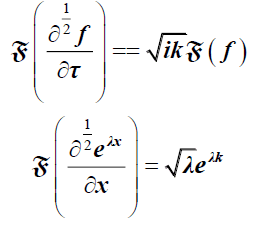 (15)
(15)
Numerical Simulation
Numerically, we have implemented these methods to approach the analytic forced and unforced flow. The problem considered, uses an analytical forcing to yield an exact solution. The test problem is set in a channel with periodic boundary condition in the x-direction and no-flow boundaries at y=0 and y=1. This geometry is the simplest setting in which to consider a slip boundary condition. A no-slip condition is prescribed at y=0, while a non-trivial slip condition is specified at y=1. Results from more complicated geometries will be reported in subsequent work.
The analytical solutions are given:
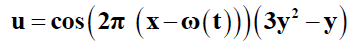 (16)
(16)
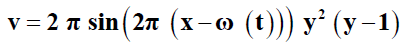 (17)
(17)
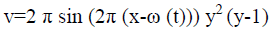
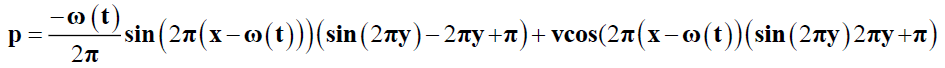 (18)
(18)
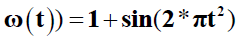 (19)
(19)
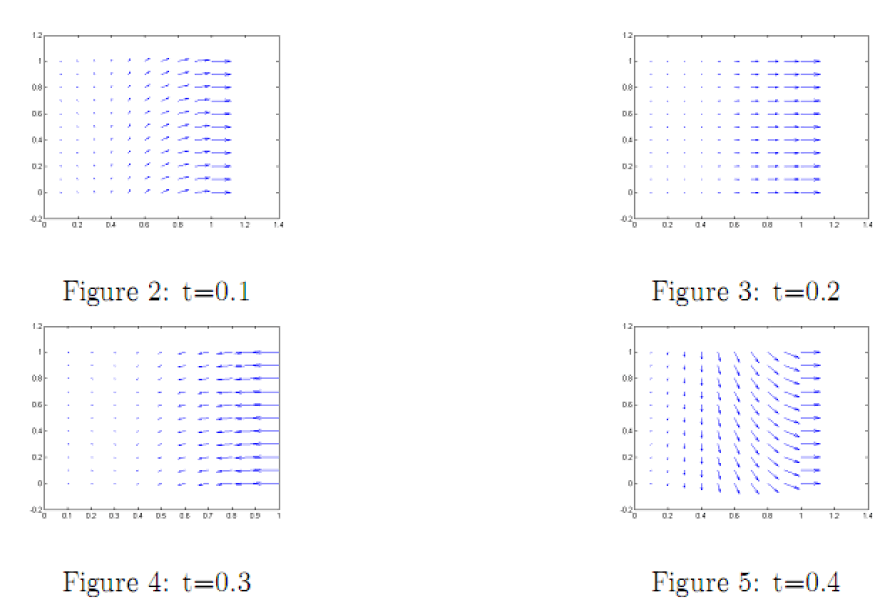
The simulation of the Navier-Stokes with viscosity ν=1 gives this result for velocity: Figure. 2 to Figure. 5.
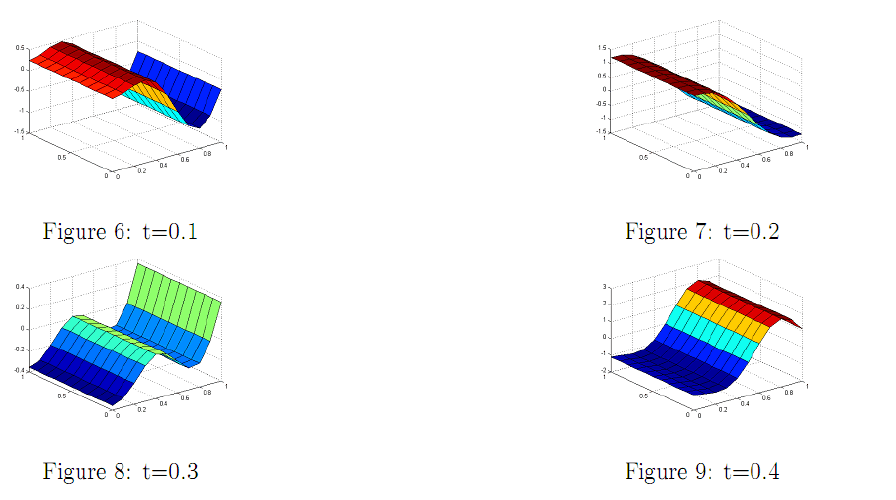
And for pressure: Figure. 6-Figure.11.
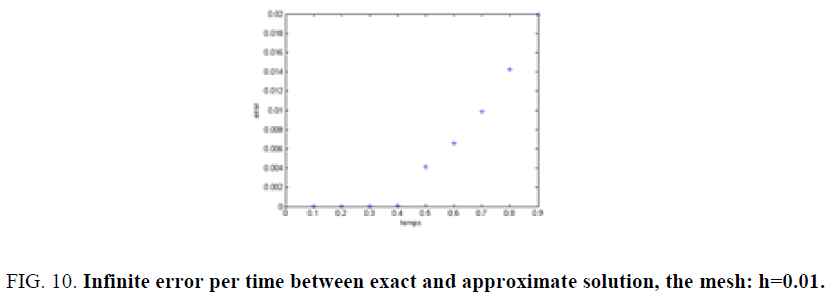
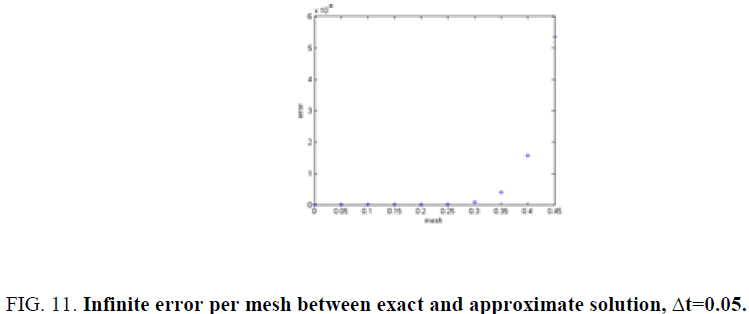
For a mesh of 62 × 64 grids and in t=0.1 s the infinite was in the order of 10-8 on some usual test-functions. This proves the efficiency of our method compared to the usual projection method. The result of the method using the proposed decomposition method are extremely fast in the order of ms. In this simulation, we have decomposed our domain in four and 16 sub domains, and we used the parallel library of MATLAB to implement the code using a core 4 duo Pentium computer [12,13].
Conclusion
In this work, we have developed a new robust algorithm applied to the non-linear Navier-Stokes equation. We firstly, prescribed a technique of splitting based on analytic transformation and the vortex method. By this way, we split our Complex Navier-Stokes equation in two simple equations: A Poisson equation and a system of separate differential equation that could be solved easily. We solved the Poisson equation by a sophisticated domain decomposition method which makes our algorithm very fast.
Secondly, we have presented several test-cases to show the efficiency of this approach. The fundamental result is that we obtained high accuracy and a fast method with a well optimized rate of convergence of the proposed algorithm in comparison with usual and classical solvers that make calculation fast.
As perspective of the present work, we can study the following ideas:
• Applying the method to turbulent flow in a square duct.
• Generalize the approach to multi-dimensional non-linear Compressible Euler equation and complex non-symmetric equation.
• Applying the method to non-linear method with complex geometries.
• Proposing a real application in fluid dynamics or environmental sciences.
References
- Chorin AJ.Numerical solution of the Navier-Stokes equations. Math Comp. 1968;22:745-62.
- Chorin AJ, Marsden JE.A Mathematical Introduction to Fluid Mechanics. 3rd ed. Springer-Verlag; 1993.
- Weinan E, Liu JG. Projection Method I: Convergence and Numerical Boundary Layers. SIAM J NumerAnal. 1995;32, (4):1017-57.
- Van KanJ.A second-order accurate pressure-correction scheme for viscous incompressible flow. SIAM J Sci Statist Comp. 1986;7:870-91.
- Karniadakis GE, IsraeliM, Orszag SA. High-order splitting methods for the Navier-Stokes equations.J Comput Phys. 1991;97(2):414-43.
- Cottet GH, Gallic SM, Raviart PA. Vortex methods for the incompressible Euler and Navier-Stokes equations.IMA Vol Math Appl. 1988;12:47-68.
- Anderson C, Greengard C.On Vortex methods. SIAM J Numer Anal. 1985;22:413-40.
- QuarteroniA, ValliA.Domain decomposition methods for partial differential equations. Oxford science publications; 1999.
- ToselliA.Domain Decomposition Methods-Algorithms and Theory. Springer; 2010.
- Gander MJ. Optimized, Schwartz Methods.SIAM J Numer Anal. 2006;44(2):699-731.
- Nataf F, Rogier F,De SturlerE.Optimal interface condition for domain decomposition methods, CMAP, EcolePolytechnique: 1994.
- Manuel D, OrtigueiraJA, MachadoT.What is a fractional derivative?J ComputPhys.2015;293:4-13.
- Zeng F, Li C. Numerical approach to the Caputo derivative of the unknown function. Cent Eur J Phys. 2013;11(10):1433-39.