Review

, Volume: 6( 3)

• View PDF
• Download PDF

The Wavelength Dependent Resolution of the Doppler in Molecular Spectrum - A New Simplified Theory of Electromagnetic Relativity

*Correspondence:

Szarycz P , Physist, Tijuana, E-Mail: Stalwart9@protonmail.com

Abstract

The subject of this paper concerns the fundamental flaws and inconsistencies in the Einstein's special and general theories of relativity which came to resemble a ptolemaic entanglement through successive addition of epicycles to present a very complicated model. Hence, a simpler, complete theory of light must exist. Naturally, I do not intend to discredit someone with the authority of Einstein and his supporters, but only one aspect of his work.

Keywords

Relativity; Molecular spectrum; Doppler; Band spread; UV spectroscopy; Tachyon; Inverse-compton

Introduction

The Einstein Lorentz connection

Einstein of course is recognized for having contributed many groundbreaking discoveries including his proof of the atomic theory by rationalizing the Brownian motion, explaining the photoelectric effect, conceptualizing the mass and energy equivalence etc. With regards to the Special Theory of Relativity however, he simply made too many assumptions and most likely he based his math on the erroneous Lorenz equations which were intended to reconcile the existence of Luminiferous Aether with the results of Michelson-Morley experiment which revealed the Aether concept to be most likely false since the speed of light was invariable regardless of the direction this light took relative to the Earth's motion, and according to the prevailing Aether theory this speed should have varied from the perspective of an Earth observer depending on whether the light was or was not travelling with the Earth through the Aether. One must recall here that in the 19th century, light was thought of strictly in terms of a wave form which by definition requires a medium - the Aether, a conjecture subsequently undermined by the theory of light first as a photon particle, and then as a hybrid wave pocket. Since light was assumed to travel and to exhibit all its properties including its velocity relative to its Aether medium and not the Earth, then if the light beam was sent in the same direction as the Earth's motion, its velocity as experienced by the Earth observer should have decreased by the velocity of the Earth along its orbit and relative to the stationary Aether. Since this was not observed by Michelson and Morley, to compensate for the unexpected results of their experiment, Lorenz consequently derived a set of equations which had an object - here the Earth and everything on it and moving with it - contract in the axis corresponding to its direction of travel through the Aether (here the Earth's orbit around the Sun) to prove that the light speed did actually vary relative to the Earth depending on whether their direction of travel aligned or not (Gribbin, 2004). But because the Earth contracted at the same time on its axis corresponding to its direction of travel through the Aether, the light beam travelling in the same direction as the Earth which should have covered less distance along the Earth's surface per unit time (Gribbin, 2004) since the Earth was moving with it through the Aether, this "slower light" would now also cover extra distance per unit time along the Earth's surface when the Earth CONTRACTED along the same axis by the same fraction as when dividing the Earth's orbital velocity by the speed of light, and the two effects would effectively cancel out, leaving the Earth observer with a false impression - according to Lorentz - that light speed does not change relative to the Earth when it travels in the same direction with the Earth through the Aether.

So what made the Lorenz ideas so attractive for Albert Einstein, that the Lorentz equations essentially formed the basis for the Special Theory of Relativity? Well, it was the hunch that there is this single entity in the universe with fixed parameters which constitutes or represents a grid, and only the light's parameters including its velocity are affixed to it (here because of the wave-medium relationship), while everything else according to Lorenz is prone to expansion or contraction or other parameter adjustments. Since light and the Aether were part of the same phenomenon and light only a disturbance in the Aether field or medium and the only part of the Aether visible to our senses or exhibited at all in our own supposed dimension (meaning the only manifestation of the Aether which our universe can interact with through the fundamental forces - a fancy theory but all hypothetical and far-fetched), once Einstein proved light to be a particle when he explained the photoelectric effect, rather than dismissing the velocity caps set upon light (just as the air limits the speed of sound waves) together with its presumed Aether medium, the next illogical step which Einstein took was to propose why not just let the light be that grid, a one single observed (as opposed to the speculative Aether) phenomenon with immutable properties which could be used as a set of definite values of universal reference, a representation of order across the universe and holding it in some form of unity? So in short, while Lorentz stipulated that the light speed is constant only in relation to its Aether medium but nothing else (light=Aether=space), Einstein tried to simplify this relationship (light=space).

Moreover, both Lorenz and Einstein started out from the assumption that there should be a grid of a universal reference - Lorenz because he believed in the Aether theory, and Einstein because he too believed light and the quasi-Aether (which he called space) to be equivalent at least as far as the mathematics are concerned (both governed by the same 3-D algebra), just one of them to be redundant from the perspective of these mathematics. They would have both made a fundamental error however, if in fact there was no grid to affix the propagation of light to begin with either through the notion that light as a wave ripple needs a medium or that light as an energy pocket is guided by a force field. And by such, no grid relationship conferring limits imposed by a medium or a force field automatically implies no velocity caps.

In hindsight, light should be placed in a proper context, which suggests that to all intent and purposes, light travels in a vacuum at a velocity c (Maxwell's Fourth Equation) relative to its emitter but not necessarily the observer. Or more concisely, all electromagnetic radiation is relative to the velocity frame of reference of their emitter, and follows a simple Euclidean geometry in tracing its trajectory relative to that emitter if outside of contact with a medium.

Thereafter came additional concerns, such as what constitutes the character of an empty space, and to what extent the force fields may play a central role in defining its dimensions and other parameters? In conceptualizing a region of space which contains nothing but a perfect vacuum (empty of any matter, radiation and fields) does the distance and the direction become irrelevant and meaningless, meaning it's all the same if this space measures a centimeter or a million miles across, straight or bent, since there is nothing inside this void to reference against? If you then added force fields across this perfect vacuum (which are now presumed to permeate space everywhere), would these fields now become the sole source of reference and consequently define the space they occupy? What if there are two competing fields operating in the same region of space, and some particles could interact with just one field, while others with both? Which field would then become dominant, and why not the other? But from the perspective of light or charged particles, what if you extended a very long straight ruler (control) from their emitter point of origin? Afterall, it is the emitter which in isolation determines all the properties and subsequent behaviour of its radiation, unless something else later acts on it. Does a straight ruler follow force fields plotting space? Let's say you attach a straight ruler to an emitter which then sends out a charged particle along the length of this ruler.

The particle later encounters a force field and its trajectory deviates away from the said ruler. Would this region of space now become defined by the ruler or the particle's trajectory? So would this behaviour be now intrinsic to or induced on the light or the particle? And then if also the ruler submitted and followed such grids defined by force fields, would it be defined by the trajectory followed by light, the gravity, or the equivalence of them both such was the case with the Aether and the light? So all such important philosophical questions were likely tackled by the General Theory of Relativity which followed - return of the Aether earlier dismissed by Einstein, by way of gravitational fields.

It seems that Einstein successfully asked all the right questions, but he was not always successful at answering them without raising doubt. For instance, what of the gravity's special status? Can it really be thought of as a force field endowed with seniority overriding all other force fields in defining the space dimension? It is understood that any single gravitational field is infinite in extent so that any single particle with mass will affect everything else with mass in the universe as long as they travel at less than the speed of light relative to each other. But this also applies to every electric field. Now, not every particle carries charge and would remain completely ignorant of electric fields, but also not everything out there has mass, such as light, and in conjunction with the WMAP and ESA’s Planck experiments which determined the universe to be flat (Wollack, 2014), the analysis of light from very distant clusters at the edge of the visible universe during the Hubble Deep Field probing for light dispersion over very long distances which would manifest itself as dispersive alteration in the image of cluster structures revealed that light does not bend (at least for reasons other than refraction) and instead follows a Euclidean geometry behaving as if gravity didn't exist at all, since some bending of light would occur over a distance of 10 billion light years if light did exhibit any smallest amount of mass. So then, mass may convert into energy, but energy in its pure state has no properties of mass. At least there was no proof ever offered otherwise beyond the scope of certain mathematics. It is true that fundamental forces are unified at higher energies, but at the temperature of the present universe the gravity and electromagnetism follow different laws and are effectively separate. They conform to a different spacial geometry and when plotting the space they span they are in competition with each other.

I have independently worked out a similar straight-forward analogy to the one provided by the Deep Field, having comprehended the assigning of emphasis on studying clusters during the Deep Field only after contemplating the gravity-induced dispersion of starlight from a single star or from nebulae. So let’s assume for a moment that if gravity were to define the behaviour of light rather than light defining space, either by warping space creating gravity wells, or by interacting with the photon’s quasi-mass derived from its kinetic energy which should endow the photon with momentum, then if we were to consider the latter case, why does light from the Sun’s photosphere seem to go straight rather than - in the extreme case - not enter an orbit around the Sun if light entirely submitted to the Sun’s gravitational field, or at the very least having its motion deflected/bent by the Sun which should then produce its warped image on Earth, and the extent of this warping should in consequence perceivably vary with the distance of the observer from the Sun, since light emitted at a greater deviation angle from the straight between the Sun's center and the observer (as from the edge of the Sun's disk) would need to warp more extensively with the increasing distance between the light source and the observer, than the light from the center of the disk having its initial trajectory aligned better with the Sun's gravitational field lines which always point towards the Sun’s core, i.e. the Earth observer, the photon emitter, and the Sun’s core all falling on the same straight line? Any deviation from this straight line in the end should produce an ever more distorted image of the Sun proportionally with an increasing distance of the observer from the Sun. Are such image dispersion/warping/smearing observed at the Hubble distances where they should be profound, since the angle of deviation between the photon’s trajectory and this straight line should grow ever larger with the increasing distance from the emitter due to a gravitational influence which is trying to force the photon into an elliptical motion around the star? This does not seem to be the case at all, judging from the sharply focussed images obtained by the Hubble of the Eagle or the Orion Nebulae for example. The same principle should apply if light is considered to have no momentum and quasi-mass, but then on the other hand to respond to the gravity-altered geometry of space. If the emitter in the photosphere does not shoot a photon straight along the line connecting the observer with the Star’s core or gravitational center, then in the process of escaping the star’s gravity well, or the warping of space, this photon should acquire some angular momentum (and initially at least some angular acceleration) in a manner of a slingshot effect causing its trajectory to gradually diverge from “the straight”, with the angle of such deviation increasing always a little with the increasing distance from the source to the observer to amplify the optical distortion effect thus inducing a diffusion of the star’s image.

So in the post-Einstein world and many epicycles later, what we have today is a light speed constant which cannot be exceeded between any two entities in the universe and is therefore a taboo necessary to account for the presumed integrity of the universe where everything in it, the particles and the fields must be able to communicate with their partners and concurrently with everything else in the universe, and maintain such communications by using photons or other slower means, ensuring cohesion of the universe so it doesn't fly apart. Light speed is therefore a magical barrier having to do with a flawed concept of the universe connected by an intrinsic velocity limit of a fastest entity out there of pure energy and no mass in relation to everything else rather than within a confined system consisting only of the photon and its emitter. Again, further analysis and concrete proof are needed that such fine cohesion across the wide universe is entirely possible, where everything is limited by the speed of light out of the necessity of communicating with each other and possibly vice versa, where the presence of fields will impose relative velocity limits on light from other sources moving at different velocities. Magnetic and electric fields do after all tend to cancel each other out as seen in magnetic fields generated by electrons orbiting the nucleus (“Concepts in Science: Electromagnetism”; episode on “Electromagnetism and Electron Flow”), and are not infinite in extent since they are made up of discrete and finite constituents - the electrons whose intensity or density will eventually fall down to zero beyond a certain distance from the source generating the field. Hence there will be regions of space where electric and magnetic fields will essentially be zero, and the photon can continue on its way unimpeded by any such field interactions which might otherwise confer velocity limits. This leaves the gravitational fields which are indeed thought of as infinite in extent, however they are not supposed to interact with photons given that photons do not have any real mass. This was bypassed by endowing photons with a quasi-mass mathematically derived from their kinetic energy which thus also gave them momentum (mass times velocity), or by having gravity indirectly influence the trajectory of photons by warping space, a concept which isn’t very clear. All conceptual and lacking proof. If all or most of what makes up the entire universe does interact and communicate with each other by using a certain medium thus allowing the universe to retain an overall macro-scale integrity, this would not be mediated by way of a real or virtual photon exchange or by another lepton exhibiting photon’s velocity.

Two types of Doppler

Returning back to the main topic of this paper, the stipulation that the velocity of light is only constant relative to its emitter (while the role of the medium will be discussed shortly), would immediately sketch a contrast between the Doppler phenomena in sound and in light, which would not be equivalent, but would come about on the basis of subtle yet key differences in wave behaviour. Sound waves are distortions in the air medium, and they always travel at a constant speed relative to the air medium which therefore limits their upper velocity, not relative to the observer or the moving emitter (similar to Lorentz' Aether). Light in the vacuum on the other hand is not limited by any medium since it is not a classical wave but instead a wave pocket which does not depend on a medium for its propagation, and neither should its velocity be limited relative to the observer.

It is best to understand the Doppler in terms of the number of wavefronts that pass through a given point, the observer, per unit time. With both light and sound the Doppler is due to the motion of the emitter, which implies that once the emitter starts moving from rest, more wavefronts pass the observer per unit time. However the difference arises on the following point. In sound, the waves are compressed both relative to each other and the observer. The Doppler is created due to the shortening of the distance between the wavefronts while the velocity of those wavefronts remains unchanged regardless of whether the emitter is moving relative to the medium or not. With light, more wavefronts pass the observer per unit time because of the velocity of the emitter which displaces the point of origin of each subsequent wave closer to the observer, but here in contrast to sound, the waves are not compressed relative to each other because they travel at a higher velocity than if they were emitted by the emitter at rest and hence "escape" the moving emitter just as fast as it is encroaching on them. They only appear compressed from the observer's experience because each subsequent wave front has less distance to cover between the emitter and the observer and hence covers it in less time leading to higher frequency as experienced by the observer. Here, the Doppler is the product of the cumulative speed of the wave (intrinsic wave speed + emitter speed) since two successive wavefronts would always remain separated from each other by the same wavelength distance, but each wavefront would take less time to cover this distance in the same direction that the emitter is moving, due to the velocity boost received from the emitter, leading to a shorter period. Or another way to put it, the Doppler here results from the intrinsic velocity of each wavefront of light relative to the emitter boosted by the velocity of the emitter relative to the observer which decreases the period between each successive wavefront hitting the observer. In sound and in light, those two different Doppler effects result in a higher pitch and a blueshift respectively.

It may sometimes be helpful to think of the Doppler in light in terms of a wavetrain which falls within the classical model. The emitter in a manner of a locomotive is pushing a wavetrain ahead of it, and the faster it goes, the more waves will cross the observer in allocated time. On the key note however, the observer can only directly experience the number of waves moving past him per second i.e. the frequency, but not the speed of the wavetrain.

One can also think of an emitter moving along together with an affixed wavetrain. The observer will detect only the peaks and valleys along this wavetrain. Because of the velocity boost provided by the emitter, the peaks and valleys will stream faster past the observer.

The total frequency of the Doppler light as experienced by the observer is then the sum of two effects, since the emitter acting as a locomotive model pushing a wavetrain ahead of it accounts only for the additional frequencies responsible for the Doppler itself. So the total frequency of the Doppler light as experienced by the observer will be the number of waves/wavefronts the emitter produces in a second, plus the number of waves in a wavetrain that the moving emitter pushes past the observer per second (or another way to put it, the number of waves which are squeezed out of the space occupied by the wavetrain connecting the emitter and the observer, when the emitter is moving). Or in strict mathematical terms, the frequency of light as experienced by the observer, is the original frequency relative to the emitter, plus this original frequency multiplied by the fraction given by dividing the velocity of the emitter relative to the observer by the speed of light, c.

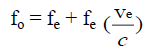(When the observer and the emitter are approaching each other)

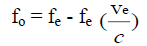(When the emitter is receding from the observer)

hence velocity of the emitter relative to the observer is given by

v_e = (f_o - f_e)/f_e * c (When approaching)

v_e = (f_e - f_o)/f_e * c (When receding)

One should also recall that although the speed of light from a stationary emitter (emitter and observer found in the same velocity frame of reference) was known since Ole Romer conducted his famous experiment by observing eclipses of the Jovian moons, yet the speed of light with red or blueshift was never experimentally determined, and in fact all that we detect on the basis of light spectrum alone is its frequency but not its velocity. And the key to measuring the relative speed of a photon is the Doppler, and some of the clearest evidence which underpins the relationship between the Doppler and the relative speed of a photon is revealed by critically deducing the band spread in molecular spectrum in different wavelengths.

The proof

It is commonly acknowledged that the molecular spectrum is subtly different from the atomic spectrum. The molecules can rotate and vibrate in complex manner - much faster than atomic motions which are usually limited to bouncing around at the speed of sound - and hence exhibit a much wider variety of spectral frequencies than atoms, providing a better testbed for studying spectral anomalies. Those additional frequencies and wavelengths associated with varying velocities in the vibrational and rotational cycles of the molecules result when electrons in atoms that constitute these oscillating molecules emit photons at constant frequencies and velocities and those velocities are then in turn superimposed against the molecule’s vibrational and rotational velocities inducing blue and red shifts in the apparent observed spectrum. The same effect can also be observed on a bigger scale in the spectrum of galaxies and Tauruses enveloping massive black holes, where the rotational velocities cause the spectral lines to broaden, and it forms the basis of the Tully-Fisher law used to determine the velocity of galactic rotation and such (Moore, 2007). In the same way, one can provide an explanation for the blue and red shifts in the microwave background radiation that results from an object’s motion relative to the epicentre of the big bang rather than a proof that the space is expanding. And the expansion of space is not synonymous with the expansion of the universe. One can be expanding without the other.

The broad band spread in the UV spectrometry

Because the UV wavelengths are so much shorter than the infrared, the superimposition of vibration and rotation of the molecules is much more pronounced with the result that bands in the UV spectra are very much broader and spread out than in the infrared spectrum that features only sharp and focused lines. In other words, the velocity and hence the Doppler of the molecule during its rotational and vibrational cycles is sufficient to affect UV wavelengths to exhibit a significant frequency spread, but carries a barely perceivable frequency spread in the infrared range due to longer wavelengths involved.

To demonstrate a common misconception concerning this difference in resolution in molecular spectrum which seems to vary with the wavelengths of the emitted light, I would like to quote from Roberts, Gilbert, Rodewall, Wingrove page 119:

“The diffusiveness of the spectrum is a consequence of the fact that electronic transitions can occur from a variety of vibrational and rotational levels of the ground electronic state into a number of different such levels of the excited electronic state. Thus, although the transitions themselves are quantized and therefore should appear as sharp “lines”, the fact that closely spaced vibrational-rotational levels give rise to closely spaced lines causes coalescence of the discrete absorptions into a band envelope to produce the broad bands observed experimentally.”

The above interpretation rationalizes the differences in observed resolution strictly in terms of the classic qualitative types of the spectral lines which were later adopted to denote the different sublevels of atomic orbitals i.e. 's' for sharp, 'p' for principle, 'd' for diffuse, and 'f' for fine [1]. Therefore the UV bands are more diffuse perhaps because electrons fall down to their ground state from several subshells of an orbital rather than one as would be observed in the infrared emission light. However, this analysis fails to explain why the electrons which generate the infrared light would prefer a single subshell which to transition from, and by the same token why the UV electronic transitions would be so much less selective, less discriminating and indeterminate in their suborbital preference? Therefore it is more plausible that the phenomenon of the UV band spread is not at all induced by the electrons falling from different types of suborbitals, but instead there is a whole different process at work. What seems to take place is a consequence of the velocity of the emitter during its vibrational and rotational cycles relative to the observer which superimposes itself against the wavelength of a constant parameter relative to the emitter. Or in other words, the culprit is the Doppler experienced only by the observer but not the emitter, and affecting the resolution of the emission spectrum to a varying degree depending on the wavelength of light, because the resolution is obtained by dividing the number of wavelengths pushed past the observer by the Doppler motion of the emitter per second, by the number of wavelengths pushed past the observer due to the photon's c velocity if the emitter was not moving relative to the observer and hence the Doppler was not present, per second. The higher the fraction, the lower the resolution, and the fraction will be higher in the UV light than in the IR.

To simplify, the molecular motions of the emitter molecules will cause the light to travel a little faster or slower relative to the observer depending on the direction the emitter is moving from the observer, and induce a greater displacement of the UV waves as a fraction of their wavelength than in the infrared. This will be manifested as spectral lines becoming more diffuse in the UV than in the IR. Another way to consider this, the observer will register slightly higher and lower frequencies than normal, and this frequency spread in a band- due to the emitter's motion - which will occur over identical time intervals in both the UV and the infrared light as registered by the observer, will affect the UV light more since it is a higher frequency light and it takes less time for a single UV wavelength to travel past the observer than for the infrared wavelength. The frequency spread takes the same amount of time to pass the observer in both types of light, but it takes less time for light in the UV to travel between two of its peaks i.e. to move two successive wave peaks past the observer, hence the frequency spread will affect a greater percentage of the UV wavelength (or fraction of the time interval to complete one cycle). As a reminder, there would be no frequency spread if photons were measured separately one at the time, but of course the detectors are tuned to show results from the input of lump sums.

The wavetrain model shuffle

And so it is, that the emission spectra are prone to varying resolution effects. But next let us quantitatively analyse how the blueshift and the redshift originate at all in the molecular spectrum in terms of the classic wavetrain model, and here you can play around with the math a bit to find a fitting though not necessarily accurate representation of what really happens, therefore the reader may find it conjectural based on an already obsolete model and somewhat of a side-track and prefer to skip over to the next section.

The frequency of light will be either intrinsic and factual, associated with the emitter's velocity frame of reference, reflecting the way the electric and magnetic fields are stacked up inside the photon wave pocket itself, or observed - associated with how the observer will experience it. In the latter case, as the excited atoms emit light, the oscillating molecular motions will extend and compress the length of the entire wavetrain of light past or short of the observer. The wavelengths from a series of wavetrains which originated from the same emitter will also compress or extend like an accordion from the perspective of an observer as I will shortly explain. The wavetrain will only be displaced on one end, the observer's end, and be fixed at the emitter's end. The length of the wavetrain will change because it represents the distance that light travels in the same amount of time that it would take light to travel from the emitter to the observer if the emitter was stationary. If the emitter approaches the observer, then the wavetrain in the emitter's velocity frame of reference will lengthen past the observer, and more wave sections will have to be added to span the length of the wavetrain, the extra length due to the motion of the emitter or the Doppler effect. If you now translate this emitter's wavetrain into the wavetrain in the observer's velocity frame of reference which has to connect the emitter with the observer, then the wavetrain in the emitter's frame of reference will have to be compressed in length, and the wave sections will also need to be compressed to accommodate the extra wave sections added to the wavetrain in the emitter's velocity frame of reference. Once you translate this into the wavetrain in the observer's frame of reference (OFR), the waves will now be shorter, the frequency higher, and you will get a blueshift. The frequency of course will be equal to the number of the wavelengths/wave sections across the entire wavetrain in the OFR divided by the number of seconds it takes for light to travel the length of the entire wavetrain at velocity c. Dividing the blueshifted frequency by the stationary emitter frequency and multiplying it by c will give you the velocity of light relative to the observer. The opposite will be true when the emitter is receding from the observer with longer wave sections and a redshift.

Now, it is important to note that the wavetrain representation describes the entire history of a single photon rather than of a series of photons intercepted by a single observer from the same source. A photon is a discrete wave section rather than spanning the length of the entire wavetrain. Moreover, one should not think in terms of peak and valley distance displacement in a continuous wave when it reaches the observer in considering what causes the band spread, because this displacement range would accumulate with increasing distance from the emitter to the observer, and hence the band spread would increase by increasing this distance, which would make any coherent spectral observation of molecules on cosmic scales quite impossible. One must think strictly in terms of the time elapsation between two successive wave peaks as they rush past the observer. Less time when the emitter molecule oscillates towards us means shift to higher frequency and shorter wavelength, and longer time when the emitter is receding from us implying a longer time between two successive peaks reaching the observer and hence redshift. But because the molecule is moving only at a fraction of the speed of light c, this time delay or time reduction between two successive peaks of a wave within a photon rushing past the observer will be a bigger fraction of the time between successive peaks in an ultraviolet light than in the infrared, giving the appearance of a greater band diffusion. This can only work however if the entire wave inside a photon is given off in "one shot", hence the front and the back end of a single photon wave will travel with the same velocity relative to either the emitter or the observer. On the other hand, successive photons given off by the same emitter do not need to reach the observer in the same sequence in which they were emitted. Some late photons may overtake others and reach the observer ahead of the early photons, especially over longer distances such as the cosmic distances.

The molecular motions of equal magnitude will induce equal but opposite displacement in the wavetrain lengths (elongation or shortening) in both the UV and IR light, since the light speed is independent of the wavelength. Moreover, the molecules experience these oscillations only at a fraction of the velocity of that of light, so the wavetrain on the whole may not be displaced by much. Despite the displacement of the entire wavetrain in both wavelengths exhibiting an exact match, the effect of this displacement on individual waves will be drastically different depending on the wavelength. In the UV light, any wavetrain displacement will be a good fraction of the UV wavelength and will significantly diffuse its emission lines rendering them their characteristic fuzzy appearance. Hence any variation in the emitter's velocity relative to the observer will have a considerable, high-sensitivity effect on the observed spectral lines. The opposite is true with the low sensitivity infrared light. Here because of the low molecular velocities versus the speed of light (c) ratio, the overall wavetrain displacement at the point of observation will remain quite small compared to any single wavelength of the IR light, and the IR lines will appear focused. Hence molecular IR radiation is robust and immune to high resolution distortions. Another way to summarize it, the distance range over which peaks or valleys of a light wave will be found as a consequence of the Doppler displacement when they reach the observer will be a good fraction of the UV wavelength, but only a small fraction of the infrared wavelength.

If the Einstein’s Theory of Relativity was correct and light propagation occurred in accordance with the time frames of reference, such frequency spread would then be absent, since light emitted by molecules at a given specific frequency should reach us always and regardless of that molecule’s vibration or rotation, with that same precise frequency. What happens instead from our velocity frame of reference, is when, during its rotational cycle, the molecule recedes from us, its apparent observed wavelength increases while the frequency decreases, and vice versa when the molecule vibrates in the direction towards us. This is what causes the frequency spread. From the emitter molecule’s velocity frame of reference however, the frequency and wavelength of the light emitted never changes.

Other possible considerations and supportive evidence

The energy transfer and velocity adjustment of tachyonic light emitted by relativistic electrons that enter a medium: The Cerenkov and Bremsstrahlung radiation: Going by the standard definition of the Bremsstrahlung type of emission: “ Photons emitted by electrons when they pass through matter. Charged particles radiate when accelerated, and in this case the electric fields of atomic nuclei provide the force that accelerates electrons. The continuous spectrum of X-rays from an X-ray tube is that of the Bremsstrahlung; in addition there is a characteristic X-ray spectrum due to excitation of atoms by the incident electron beam. The angular distribution of Bremsstrahlung is roughly isotropic at low electron velocities, but is largely restricted to the forward direction at high velocities. Very little Bremsstrahlung is emitted at an angle much larger than θ = m(electron)c²/T radians ” [2]. There is a similar pattern with respect to the direction of emission observed in the Cherenkov radiation: “ Cherenkov radiation is emitted at a fixed angle θ to the direction of motion of the particle such that cos θ = c/nv, where v is speed of the particle and n is index of refraction of the medium. The light forms a cone of angle θ around the direction of motion. If this angle can be measured, and n is known for the medium, the speed of the particle can be determined i.e. v = c/ncosθ “ [2].

One way to interpret these results is to assume that at slow, non-relativistic velocities the detector will register an equal distribution of radiation given off by the electron in all directions in relation to that electron. At relativistic velocities however, the distribution of radiation from the said electron remains even, but the detector will pick up more intensive radiation when the electron travels more or less towards it, and much less when the electron recedes from it, because radiation emitted by the electron in direction of the detector will be stretched out or redshifted towards much longer wavelengths which the X-ray detectors are not tuned to pick up. This radiation may be registered by say, the UV or the infrared apparatus, and beyond this at the microwave or radio frequencies it may blend in with the background noise emitted from ordinary objects. From the point of view of relativistic electron though, the wavelength of radiation it gives off in any direction has not changed at all, and the angle θ is not limited by the electron’s kinetic energy. What did change was the much reduced relative speed between the photon and the detector and hence increasing the photon’s wavelength from the detector’s frame of reference. If one were to eliminate most of the background radiation and set up an array of detectors with sensitivities corresponding to various longer wavelengths from UV to radio, one just might find the “missing” radiation, which in terms of intensity of photons given off should be uniform in all directions, similar to what you find at the slower electron velocities.

One can also speculate on whether the Cherenkov and Bremsstrahlung emissions are not the result of excitation of atoms in the medium by photons given off by the electrons that travel at relativistic speeds? These medium atoms would then give off a secondary radiation. Such atoms would need to be heavy however to account for radiation in the X-ray range, and the type of media used in the experiments testing for the said emissions most often consists of lighter atoms. Moreover, the X-rays would then have to be of a specific frequency in correspondence to the types of atoms that were excited, whereas the X-ray frequency range of the Cherenkov and Bremsstrahlung radiation is probably continuous. This secondary radiation hypothesis therefore falls short.

The impact of diffuse medium on blueshifted light in low and high energy settings

Considering now how a photon of high energy, say an X-ray or a gamma ray would pass too close to a nucleus of an atom, it would then convert to particle pairs (Britannica, vol.10, def’n of Light, p.551-558). Since light from a moving emitter will be blueshifted from the perspective of an encountered atomic nucleus, it would then convert even more readily. This is why light can travel in excess of c, but often fails to reach us because we don't sit in a vacuum but are instead surrounded by medium of all sorts, from an atmosphere to the solar wind. Or rather, any blueshifted light we detect travels in excess of c relative to us, but we have no way to measure its speed directly since we can only measure its frequency i.e. the number of "wavefronts" passing us per unit time. And much of the highly blueshifted light will never reach us (unless it starts out as low frequency radiation, say in the radio or the microwave range in the emitter's velocity frame of reference) since it will usually convert to particle pairs once it encounters any medium in our velocity frame of reference, due to its particularly high energy.

When on the other hand a photon exhibiting less exotic energy encounters a medium, it may have one of three supposed effects. It may excite electrons which is how they invented semiconductors; it may excite the atom’s nucleus that would subsequently de-excite by giving off gamma rays - which has not been observed and may have something to do with the conservation of energy [2]; or when a photon carries higher energy - possibly as a result of its increased frequency due to its velocity in excess of c relative to anything it encounters - yet alone insufficient to convert to particle pairs, this photon may nevertheless find a way to undergo conversion to particles in the manner as quoted below:

“ e+ /e- pairs can be created from gamma rays, by collision of two heavy particles, a fast electron passing through the field of a nucleus, the direct collision of two electrons, the collision of two light quanta in a vacuum “ [3].

Normally, you need a photon in the gamma ray frequency range, with at least 1.02 MeV energy to produce an e+ /e- pair. But then if you carefully direct two less exotic photons at each other head on, which separately have insufficient frequency and energy to produce e+ /e- pairs, lone behold, you end up with this two-photon interaction spitting out e+ /e- pairs. It’s as if one photon was held stationary, and the other’s frequency or speed were doubled and λ halved. Or if one photon assumed the role of a nucleus and the other was promoted to a gamma ray status passing nearby, not unlikely due to its frequency boost provided by doubling of its velocity. The GTR would have it on the other hand, that you cannot have such a doubling of the velocity or frequency with respect to another particle, as nothing can exceed the speed of light.

So one can infer from all these observations, that a photon which is moving at a speed highly in excess of the value c relative to the medium, that it cannot travel for a long distance inside this medium before encountering medium atoms within close range, causing the photon to either becoming absorbed by the electrons inducing photoelectric effect allowing electrons to escape their atoms hence ionizing them which surely happens in places like the heliopause, or such photons would instead convert into electron/positron pairs, muons or pions in collisions with other photons emitted by the surrounding medium electrons depending on their combined incident energy of at least 1.02 MeV, or through close encounters with the nuclei provided that these photons are high energy carriers either due to a significant blueshift or their high energy emitter, or a combination of both. If neither restriction is breached then light can proceed without interference through the medium at the velocity in excess of c relative to this medium. This can be said with a great deal of certainty about diffuse medium, while dense medium may or may not present a more complicated scenario.

The group and phase velocities of light

“The quantity of the c constant can be measured either by c = Δd/Δt (group velocity) or c = frequency/wavelength (phase velocity). The group velocity for light that travels through a medium will come out smaller (by 1.5% in water, 2.4% in glass etc.) than the phase velocity unless measurements are carried out in a nondispersive medium in which velocity is the same for all wavelengths. The experimental values determined by the two methods are at an admitted and disturbing variance with one another” [2].

Since the group and phase velocities of light that travels in a medium are by no means interchangeable, and are known to diverge due to the dispersive effect associated with the index of refraction of the media that the light travels through, by the same token there is also no reason to doubt why the group and the phase velocities should also not differ due to the motion of the light emission source relative to the observer, where the emission source and the observer are separated only by a vacuum. The phase velocity, will always be c in a vacuum or c/n in a given medium, but the group velocity can vary with the relative velocity of the source of emission.

The Doppler-Fitzeau effect

“ If the source moves away from the observer with a velocity (v) that is small compared with the velocity of light, then the length of the wavetrain increases so as to be numerically equal to the sum of the two velocities (c + v) and the number of waves remains the same. The wavelength λ increases to λ’ by a factor (c + v)/c; that is λ’ = (1 + v/c)λ ”[3].

This law assumes that the number of wavelengths in the wavetrain between the receding source and the observer as compared with a stationary source would remain the same. In other words, when the source and the observer begin to recede from one another, the number of cycles or the frequency of light as it traverses the expanded gap between the two, would remain unaltered. On the other hand, the wavelengths are assumed to have increased, while the speed of light is assumed to have remained the same. This law has formed the basis for the Lorentz equations which in turn laid the foundations for the General Theory of Relativity which soon followed. A more correct interpretation however would have the number of wavelengths in the wavetrain between the receding emission source and the observer increase, but then from the perspective of the emission source, the frequency, the wavelength and the speed of light would remain unaltered, while from the perspective of the observer, the wavelength shortens, the frequency remains the same, and the speed of light decreases, taking the light more time to close the gap due to a decreased distance the light travels through in each cycle.

The Poynting Vector

A Poynting vector (S) is equivalent to Є times H as well as velocity of the electromagnetic radiation v(EM) times W, where v(EM) is the velocity of EM waves and W is the energy density [3]. S can also be thought of in terms of the energy crossing a unit area in unit time [3].

If we register the light that is redshifted, the energy crossing a unit area per unit time will be reduced compared to the energy of a non-red-shifted light, because redshift implies a reduction of energy. Since both the dielectric constant and the strength of the electric field of photons don’t change (in the latter case because the amplitude of planar waves doesn’t change in relation to the distance propagated from the source; that only applies to spherical waves which the light is not [3]), the energy density (W) will remain the same, since it’s equivalent to W = εЄ² [3], which implies that the speed of the redshifted light has decreased to account for reduced S.

The Inverse Compton scattering

“ Rich clusters of galaxies are generally X-ray sources which result from combination of radiation from a very hot (100 million K) gas filling intergalactic space, as well as of emission from a few discrete sources. Each source radiates by a mechanism known as inverse Compton scattering, which can add energy to low-energy photons, converting them to X-rays. It does this through the interaction of the photons with electrons that are moving at relativistic velocities” [4].

In contrast to the well understood Compton effect where the higher energy incident photons transfer part of their momentum and energy to the electrons they collide with and henceforth bounce off them but now acquiring longer wavelengths, here with the Inverse Compton scattering it is quite conceivable that there is a process involved in the inter-galactic space which builds up electric potential which subsequently discharges. This process involves highly diffused charged gas particles which encounter very little friction and thus move at a very high velocity relative to the Earth or any stars in the neighbouring galaxies. Normal-energy incident photons from neighbouring stars or nebulae are initially absorbed at frequencies adjusted to the velocity of the intergalactic gas, this absorption taking place over time involving several photon absorptions and in the process building up voltage potential, and once this voltage exceeds a certain threshold, energy is released in form of photons boosted up by the velocity of the emitter electrons to X-ray frequencies in the Earth observer’s velocity frame of reference. The electric discharge may thus occur by a similar mechanism as the one used to explain how radiation beams are hypothetically generated by fast spinning millisecond pulsars as proposed by Donald E. Scott [5]. Alternatively, the photons may be emitted simply when protons and electrons or two different electrons pass too close to each other at very high velocities or when these charged particles simply encounter electric or magnetic fields of any kind that would induce their angular acceleration which generates photons. If the approaching electron and the field it encounters find themselves in very much different velocity frame of references, this alone could generate the Inverse-compton photons even if the field and the Earth observer are in a similar velocity frame of reference. Again, this frequency boosting is due to the cumulative velocity of the Inverse-compton photons which combines the speed of light, c, with the electron’s “relativistic” velocity, provided that the said electrons are moving in a fairly head on direction towards the Earth at the instance when they emit or re-radiate the Inverse-compton photons. The frequency of the Inverse-compton photons of a value f_s in the velocity frame of reference of the source electrons (photon frequency at the source) will be adjusted in the velocity frame of reference of the observer or fo according to f_o = f_s + f_s * (vscosθ/c), where θ is the angle between the line of sight connecting the Earth observer and the emitter electron, and the deviation in the direction of travel of the electron from that line. v_s is velocity of the electron relative to the Earth observer.

As an emitter nears the speed of light relative to a receding observer, the time it takes for the light that travels in the direction of the observer to reach this observer would equally increase and approach infinity. If the electric and magnetic fields inside the photon’s wave pocket are imprinted, then to the observer who can only measure photon’s frequency but not its velocity its wavelengths would appear close to infinity and frequency close to 0. By the Doppler – Fitzeau effect analogy, the length of the waves in the wavetrain would increase exponentially and finally reach infinity. This may apply perhaps in studying radio waves where according to a classical interpretation the shape of the wave is synonymous with the orbiting motions of the emitter electron. This would also have an impact when studying objects at the very edge of the visible universe whose UV and visible light spectrum may have shifted into radio wavelengths [6].

Alternatively, one should pause here and recall that the curvature of the photon wave represents the strength and direction of the electric field across a given space, as well as its affiliated but much weaker magnetic field. Rather than being imprinted in the inner space of the photon’s wavepocket, those fields are thought to reverse in intensity back and forth between electrical and magnetic which is what is thought that allows the photon to propagate along through space. Consequently, if the emitter attained relativistic receding velocities relative to the observer, once the photon had reached the observer, this observer would experience photon's frequency equal to the sum of the frequency of its emitter electron's oscillations plus the number of wavelengths in the photon’s wave passing by the observer per second. The classic wavetrain model would fail here at the receding relativistic velocities, since technically the photon wave would have to undergo almost an infinite number of oscillation cycles before reaching the observer, and the wavetrain would need to be divided into an infinite number of wavelength sections [7-12].

Conclusion

In hindsight, light does not determine, outline or trace geometry of the universe since it cannot interact with gravity which also means that gravitational fields cannot slow down and impose velocity limits on light, and light does not impose the ultimate velocity limit on everything else in the universe. Likewise, the properties of light are set only relative to its emitter and light can exceed the velocity of c relative to anything else except its own emitter as long as it is in a vacuum without electric or magnetic fields present. Upon encountering fields light may still travel in excess of c unimpeded as long as its energy does not exceed certain threshold values starting with ones equivalent to the potential energy difference between electron orbitals resulting in the absorption of the photon by these electrons. Then if its frequency boosted by its velocity relative to the radiation within the fields or nuclei at close encounters is sufficient, the photon may then convert into particles before it gets a chance to ionize an electron. The overall scenario at higher energies gets complicated, but given the right conditions, light can travel through a medium in excess of c. The X-rays in Cherenkov radiation and the molecular spectrum up to the UV wavelengths seem to meet such conditions.

The mistake which some physicists could have made was to consider problems and phenomena associated with light in relativity settings in terms of wavelengths, but it’s much more helpful to consider them in terms of frequencies, since the actual speed of photons relative to the observer’s speed frame of reference and hence their actual wavelengths are often unknown to the observer in situations where the relative velocity of the emission source remains uncertain. Examining relativity from the perspective of wavelengths of light may lead to speculation about how space may behave much like a wave which quite easily stretches or contracts.

Since the speed of light is not a universal constant but varies in the context of which velocity frame of reference it is referred to, then the light cannot link space distances and time together, whereby changing the value of one will automatically impact the value of the other, which means that space and time are not equivalent. The Lorenz and Einstein’s Special Relativity static formulas which attempted to accomplish this by keeping the velocity of light always at the constant c regardless of which velocity frame of reference was considered, observer’s or the emitter’s, and thus forcing d and t to change instead by way of c = d/t in order to maintain the velocity of light always at c regardless of what is referenced against, are fundamentally flawed by making this wild assumption where space-time = constant and therefore space and time becoming synonymous. This is what may be described as a photon-oriented universe. Examining the universe from perspective of a photon, where dimensions of space are altered to maintain the c velocity constant regardless of the reference point context represented either by the emitter or the observer.

Saving best for last, here is the breakdown of the Einstein hoax. Naturally, you cannot maintain light’s velocity at a c constant (in the observer’s velocity frame of reference who is moving relative to the emitter, and let’s say they are approaching thus increasing the distance that light covers relative to the observer each second) if you increase distance and decrease time or vice versa. Both d and t need to either increase or decrease simultaneously. Then again, only the numerator and denominator both need to increase. But Lorenz wanted space to constrict at increased velocity while keeping the time constant in order to counteract the effects of greater real distance so that light would always experience this distance which it spans as 300,000 km per second. Then he realized further that t too could be adjusted instead of d just for the sake of it since going either way will have the same impact on the c constant. Then Einstein deduced that both d and t could be adjusted simultaneously to keep the velocity of light always at the c constant. The easiest thing would be to start from c = d * t or c = (dx)(dt) = (1/2)(2) if you’re going to make space shrink and time expand to cancel out each change, but that would defy common sense! Yet this is exactly what Einstein proposed: not space over time but space-time yields a constant. Here v becomes a derivative of c, and c doubles down either as acceleration or a “natural motion” perhaps due to gravity, so trajectory traced by the motion of light defines the curvature of space caused by gravity. This was all an elaboration of what Lorentz postulated who wanted to rework the v = d/t into something like c = d/(1 - Δ t), or c = d/(1 - Δ t)2 but then noticed after changing the values at increased velocity that the numerator and denominator still did not run in parallel to cancel each other out since only one could be kept as a function and its derivative prone to change according to his concept of the Aether universe. Work it, work it and eventually up becomes down and maybe by accident you will get a constant, keeping v always at c. But it hasn’t happened yet, not without profound conceptual errors.

Presuming that everything will convert their mass into energy proportionally with their velocity as a fraction of the speed of light and then proportionally experience shrinking space up to half (a nice, round, magic number, as if the neatness of which is supposed to lend credibility to the concept, but the universe seems more random than this) of the normal space and extended time up to twice (magic number) the normal time is simply a wishful thinking. This line of reasoning says that everything will become more like light and less its normal self as their velocity increases, and in the process proportionally experience a different universe with fluid parameters, or even changing those parameters as the universe might experience them by the very act of acquiring velocity. This contradicts observations since electrons accelerated in synchrotrons or in Van Allen belts (Karen C. Fox, 2013) close to the speed of light seem not to exhibit the properties of pure energy of light at all, but behave instead much like any normal electrons around stationary nuclei which attain only one percent of the speed of light (Carl Zorn). Fiddling around with the math taken out of context or proper reference or math impaired by deriving it from hit and miss models imposes its own limitations.

References

1. Eric WW. The section on general quantum mechanics.1996-2007.
2. Sybil PP. McGraw-Hill encyclopedia of Physics, McGraw-Hill Book Company, New York. 1983.
3. Encyclopedia Britannica, Helen Hemingway benton publisher, University of Chicago. 1975.
4. Jay MP. Contemporary Astronomy, 2nd ed., Williams College-Hopkins Observatory, Williamstown, Massachusetts, Sounders College Publishing. 1981.
5. Donald ES. The Electric sky: A challenge to the myths of modern Astronomy, Mikamar Publishing.2006.
6. Royston MR, John G, Lynn BR, et al. Modern experimental organic chemistry third edition, Sounders College, Philadelphia. 1979.
7. William K. Concepts in Science: Electromagnetism, A production of TVO. 1987.
8. Moore SP. Philip?s Atlas of the Universe (6th ed. softcover). 2007.
9. Gribbin J. The Scientists, random house trade paperbacks. 2004.
10. Fox KC. Nasa's van allen probes discover particle accelerator in the heart of earth?s radiation belts. NASA. 2013.
11. Zorn C. Questions and answers: how fast do electrons move?, Jefferson Lab.
12. Wollack EJ. Measurements from WMAP, NASA. 2014.