Review
, Volume: 14( 3)The Gravity Waves from the Binary Galaxies-The New Deal of the James Webb Space Telescope
The Gravity Waves from the Binary Galaxies-The New Deal of the James Webb Space Telescope
Miroslav Pardy*
Department of Physical Electronics, Masaryk University, Brno, Czech Republic *
Corresponding author: Miroslav Pardy, Department of Physical Electronics, Masaryk University, Brno, Czech Republic, Email: pamir@physics.muni.cz
Received: July 02, 2024, Manuscript No. TSSE-24-140480; Editor assigned: July 05, 2024, PreQC No. TSSE-24-140480 (PQ); Reviewed: July 22, 2024, QC No. TSSE-24-140480; Revised: June 02, 2025, Manuscript No. TSSE-24-140480 (R); Published: June 10, 2025, DOI. 10.37532/2320-6756.2025.14(3).388
Abstract
The energy spectrum of gravitons emitted by the black hole binary as a gravity waves is calculated in the first part of the article. Then, the total quantum loss of energy, is calculated in the Schwinger theory of gravity. Using analogy with the binary stars, we calculate the graviton spectrum of the binary galaxies discovered by the JWST of NASA.
Abstract
The energy spectrum of gravitons emitted by the black hole binary as a gravity waves is calculated in the first part of the article. Then, the total quantum loss of energy, is calculated in the Schwinger theory of gravity. Using analogy with the binary stars, we calculate the graviton spectrum of the binary galaxies discovered by the JWST of NASA. Keywords: Binary stars; Binary galaxies; JWST; Graviton; Schwinger source theory Journal of Space Exploration Review Article | Vol 14 Iss 3 The Gravity Waves from the Binary Galaxies-The New Deal of the James Webb Space Telescope Miroslav Pardy* Department of Physical Electronics, Masaryk University, Brno, Czech Republic * Corresponding author: Miroslav Pardy, Department of Physical Electronics, Masaryk University, Brno, Czech Republic, Email: pamir@physics.muni.cz Received: July 02, 2024, Manuscript No. TSSE-24-140480; Editor assigned: July 05, 2024, PreQC No. TSSE-24-140480 (PQ); Reviewed: July 22, 2024, QC No. TSSE-24-140480; Revised: June 02, 2025, Manuscript No. TSSE-24-140480 (R); Published: June 10, 2025, DOI. 10.37532/2320-6756.2025.14(3).388 Introduction A binary star is a system of two stars that are gravitationally bound to and in orbit around each other. Binary stars-a single object to the naked eye-are often resolved using a telescope as separate stars, in which case they are called visual binaries. Many visual binaries have long orbital periods of several centuries and therefore have orbits which are uncertain or poorly known. They may also be detected by indirect techniques, such as spectroscopy-spectroscopic binaries or astrometry-astrometric binaries. If a binary star happens to orbit in a plane along our line of sight, its components will eclipse and transit each other; these pairs are called eclipsing binaries or together with other binaries that change brightness as they orbit, photometric binaries. If components in binary star systems are close enough they can gravitationally distort their mutual outer stellar atmospheres. Double stars, a pair of stars that appear close to each other, have been observed since the invention of the telescope. Mizar, in the Ursa Major, was observed to be double by Giovanni Battista Riccioli in 1650 and earlier by Benedetto Castelli and Galileo. The double star Acrux, in the Southern Cross, was discovered to be double by Father Fontenay in 1685. William Herschel began observing double stars in 1779. Over the years, many more double stars have been cataloged and measured. As of June 2017, the Washington double star catalog, a database of visual double stars compiled by the United States Naval Observatory, contains over 100000 pairs of double stars, including optical doubles as well as binary stars. Our goal is not to consider the binary stars but binary galaxies discovered by JWST. www.tsijournals.com | June-2025 2 Literature Review Binary galaxies A galaxy is a system of stars, stellar remnants, interstellar gas, dust and dark matter bound together by gravity. Galaxies, averaging an estimated 100 million stars, range in size from dwarfs with less than a hundred million stars, to the largest galaxies known super giants with one hundred trillion stars, each orbiting its galaxy’s center of mass. Most of the mass in a typical galaxy is in the form of dark matter, with only a few percent of that mass visible in the form of stars and nebulae. Super massive black holes are a common feature at the centers of galaxies. Galaxies are categorized according to their visual morphology as elliptical, spiral or irregular. Many are thought to have super massive black holes at their centers. It is estimated that there are roughly 200 billion galaxies in the observable universe. Most galaxies are 1000 to 100000 parsecs in diameter and are separated by distances on the order of millions of parsecs or mega parsecs. For comparison, the Milky Way has a diameter of at least 26800 parsecs and is separated from the Andromeda Galaxy (with diameter of about 152000 ly), its nearest large neighbor, by 780000 parsecs. James Webb Space Telescope–JWST JWST is able the detailed observations of distant and ancient galaxies. The telescope’s improved capabilities enable scientists to study the structures, properties and dynamics of these galaxies with remarkable precision. This revolutionizes our ability to unravel the mysteries of the early universe and gain insights into the processes that shaped cosmic evolution. The JWST observations have revealed a staggering number of galaxies, surpassing earlier estimates. The JWST allows to observe distant objects that emit light at longer wavelengths. This enables the detection of ancient galaxies that have undergone significant redshift due to the expansion of the universe. At the same time, the JWST allows to observe galaxies forming the binaries and radiating the gravity waves. This is the new deal of JWST. The telescope’s enhanced resolution and sensitivity provide clearer and more detailed images of these galaxies, unveiling their structures and properties with unprecedented clarity. The discovery of thousands of galaxies in the GOODS-South region provides a wealth of data for studying cosmic evolution. By examining the properties and distribution of these galaxies, researchers can gain insights into how galaxies formed, evolved, and interacted in the early universe. This information helps piece together the puzzle of cosmic evolution and contributes our broader understanding of the universe’s history. Black holes In 1916, Schwarzschild published the solution of the Einstein field equations Schwarzschild, 1916 that was later understood to describe a black hole and in 1963 Kerr generalized the solution to rotating black holes [1]. The year 1970 was the starting point of the theoretical work leading to the understanding of black hole quasi normal modes and in the 1990 higher-order postNewtonian calculations Blanchet was performed and later the extensive analytical studies of relativistic two-body dynamics realized [2]. These advances, together with numerical relativity breakthrough in the past decade [3]. Numerous black hole candidates have now been identified through electromagnetic observations [4]. The black hole binary and their rotation and et al. mergers are open problem of the astrophysics and it is the integral part of the binary black hole physics. The binary pulsar system PSR B1913+16 (also known as PSR J1915+1606) discovered by Hulse and Taylor and subsequent observations of its energy loss by Taylor and Weisberg demonstrated the existence of gravitational waves [5]. By the early 2000’s, a set of initial detectors was completed, including TAMA 300 in Japan, GEO 600 in Germany, the Laser Interferometer Gravitational-Wave Observatory (LIGO) in the United States and Virgo in Italy. In 2015, Advanced LIGO became the first of a significantly more sensitive network of advanced detectors (a second-generation interferometric gravitational wave detector) to begin observations [6]. www.tsijournals.com | June-2025 3 Taylor and Hulse, working at the Arecibo radio telescope, discovered the radio pulsar PSR B1913+16 in a binary, in 1974 and this is now considered as the best general relativistic laboratory [7]. Pulsar PSR B1913+16 is the massive body of the binary system where each of the rotating pairs is 1.4 times the mass of the Sun. These neutron stars rotate around each other in an orbit not much larger than the Sun’s diameter, with a period 7.8 hours. Every 59 ms, the pulsar emits a short signal that is so clear that the arrival time of a 5-min string of a set of such signals can be resolved within 15 µs. A pulsar model based on strongly magnetized, rapidly spinning neutron stars was soon established as consistent with most of the known facts gold its electrodynamic properties were studied theoretically Goldreich and shown to be plausibly capable of generating broadband radio noise detectable over interstellar distances. The binary pulsar PSR B1913+16 is now recognized as the harbinger of a new class of unusually short-period pulsars, with numerous important applications. Because the velocities and gravitational energies in a high-mass binary pulsar system can be significantly relativistic, strong-field and radiative effects come into play. The binary pulsar PSR B1913+16 provides significant tests of gravitation beyond the weakfield, slow-motion limit [8]. We do not here repeat the derivation of the Einstein quadrupole formula in the Schwinger gravity theory [9]. We show that just in the framework of the Schwinger gravity theory it is easy to determine the spectral formula for emitted gravitons and the quantum energy-loss formula of the binary system. The energy-loss formula is general, including black hole binary and it involves arbitrarily strong gravity. Since the measurement of the motion of the black hole binaries goes on, we hope that sooner or later the confirmation of our formula will be established. The spin 2 gravity in source theory Source methods by Schwinger are in source theory adequate for the solution of the calculation of the spectral formula of gravitons and energy loss of binary. Source theory Schwinger et al., was initially constructed to describe the particle physics situations occurring in high-energy physics experiments. However, it was found that the original formulation simplifies the calculations in the electrodynamics and gravity, where the interactions are mediated by photon and graviton respectively. The source theory of gravity forms the analogue of quantum electrodynamics because, while in QED the interaction is mediated by the photon, the gravitational interaction is mediated by the graviton Schwinger. The basic formula in the source theory is the vacuum-to-vacuum amplitude [10]: where the minus and plus symbols refer to any time before and after region of space-time with action of sources. The exponential form is postulated to express the physically independent experimental arrangements, with result that the associated probability amplitudes multiply and the corresponding W expressions add. where the minus and plus symbols refer to any time before and after region of space-time with action of sources. The exponential form is postulated to express the physically independent experimental arrangements, with result that the associated probability amplitudes multiply and the corresponding W expressions add. 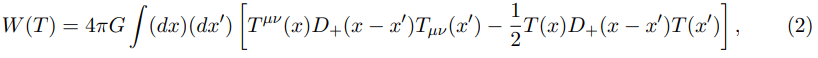In the flat space-time, the field of gravitons is described by the amplitude (1) with the action (c=1 in the following text): www.tsijournals.com | June-2025 4 where the dimensionality of W (T) has dimension of the Planck constant h¯ ; Tµν is the momentum and energy tensor that, for a particle trajectory x=x(t), is defined by the equation: where pµ is the relativistic four-momentum of a particle with a rest mass m and and the relativistic energy is defined by the known relation where v is the three-velocity of the moving particle. Symbol T (x) in formula (2) is defined as T=gµνT µν, and D+(x − xr ) is the graviton propagator whose explicit form will be determined later. The graviton spectrum of the black hole binary It may be easy to show that the probability of the persistence of vacuum is given by the following formula: where the so-called power spectral function P (ω, t) has been introduced. For extraction of the spectral function from Im W, it is necessary to know the explicit form of the graviton propagator D+(x−xr ). This propagator involves the graviton property of spreading with velocity c. It means that its mathematical form is identical with the photon propagator form. With regard to Schwinger et al. the x-representation of D(k) in eq. 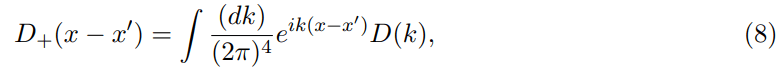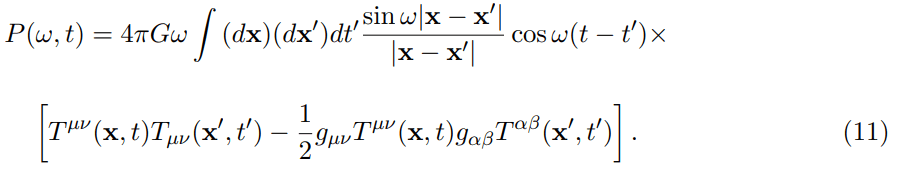(2) is as follows: Where which gives www.tsijournals.com | June-2025 5 Now, using formulas (2), (7) and (10), we get the power spectral formula in the following form: The power spectral formula for the binary system In the case of the binary system with masses m1 and m2, we suppose that they move in a uniform circular motion around their center of gravity in the xy plane, with corresponding kinematic coordinates: For the tensor of energy and momentum of the binary we have: 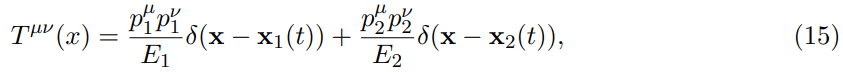where we have omitted the tensor tG µν, which is associated with the mass-less, gravitational field distributed all over space and proportional to the gravitational constant G: After insertion of eq. (15) into eq. 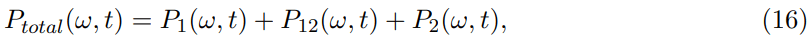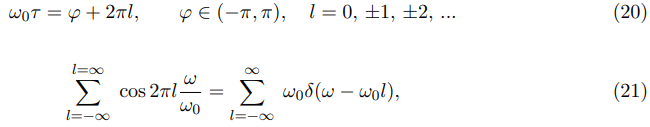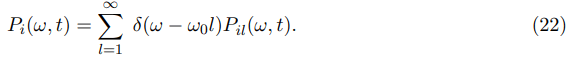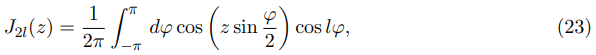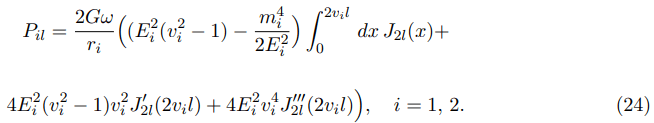(11), we get (Pardy, 1983): where (t’ −t=τ): www.tsijournals.com | June-2025 6 The quantum energy loss of the binary Using the following relations we get for Pi (ω, t), with ω being restricted to positive: Using the definition of the Bessel function J2l(z) from which the derivatives and their integrals follow, we get for P1l and P2l the following formulas Using r2=r1+?, where ? 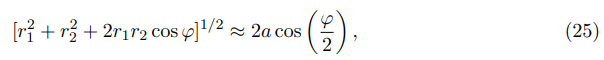is supposed to be small in comparison with radii r1 and r2, we obtain With So, instead of equation. 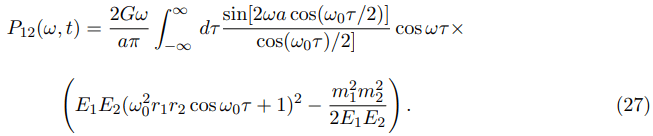(19) we get: Now, we can approach the evaluation of the energy-loss formula for the binary from the power spectral formulae (24) and (27). 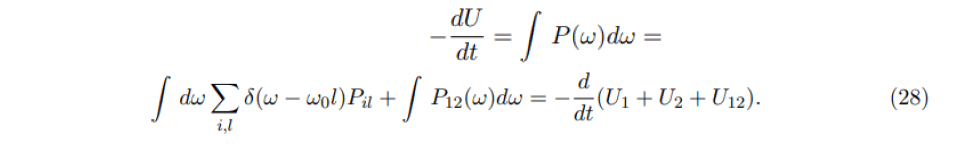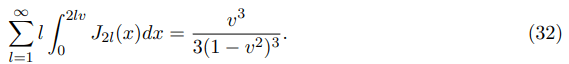www.tsijournals.com | June-2025 7 The energy loss is defined by the relation From the book of formulas (Prudnikov et al., 1983) we have Kapteyn’s formula After differentiating the last relation with respect to v, we have We learn other Kapteyn’s formulas Prudnikov et al.: and So, after application of eqs. (30), (31) and (32) to eqs. (24) and (28), we get: Instead of using Kapteyn’s formulas for the interference term, we will perform a direct evaluation of the energy loss of the interference term by the ω-integration in (27). 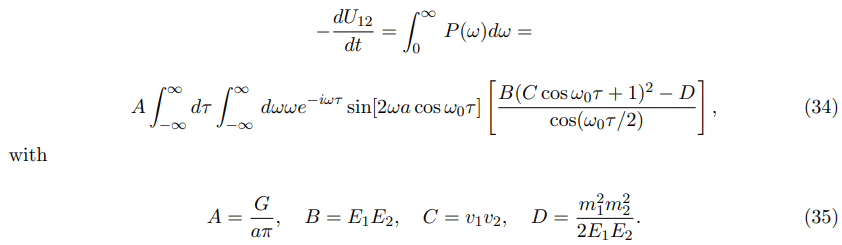So, after some elementary modification in the ω-integral, we get: www.tsijournals.com | June-2025 8 Using the definition of the δ-function and its derivative, we have, instead of eq. 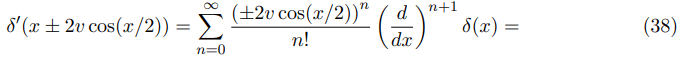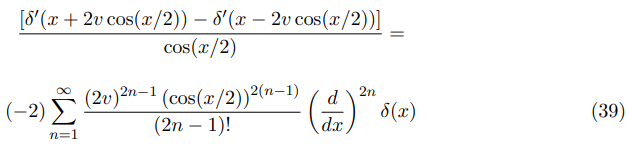(34), with v=aω0: According to the Schwinger article Schwinger, we express the delta-function as follows: Then and it means that Now, we can write eq. 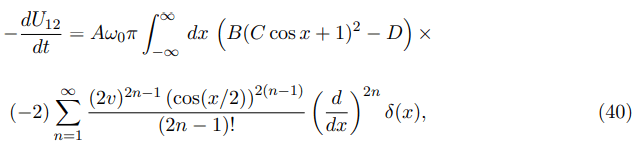(36) in the following form after some elementary operations where B (C cos x + 1)2 −D can be written as follows: After application of the per partes method, we get from eq. (40) the following mathematical object: www.tsijournals.com | June-2025 9 We get after some elementary operations ∫δf (x)=f(0) where f, g, h, F, G, H are functions which must be determined So we get instead of eq. (41) the following final form Let us remark that we can use simple approximation in eq. (41) as follows: (cos(x/2))2n+2 ≈ (cos(x/2))2 , (cos(x/2))2n ≈ (cos(x/2))2 , (cos(x/2))2(n—1) ≈ (cos(x/2))2 . 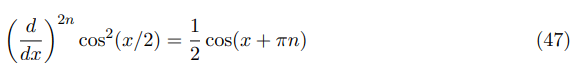Then, after using the well-known formula and So, instead of eq. (46) se have: www.tsijournals.com | June-2025 10 Discussion We have derived the spectral density of gravitons and the total quantum loss of energy of the black hole binary. The same formulas are valid for galaxy binaries which can be modelled as the two-body system. The energy loss is caused by the emission of gravitons during the motion of the two black hole binary around each other under their gravitational interaction. The energy-loss formulas of the production of gravitons are derived here by the Schwinger method. Because the general relativity and theory of gravity do not necessarily contain the last valid words to be written about the nature of gravity and it is not, of course, a quantum theory Taylor they cannot give the answer on the production of gravitons and the quantum energy loss, respectively. So, this article is the original text that discusses the quantum energy loss caused by the production of gravitons by the black hole binary system and by the galaxy binary. It is evident that the production of gravitons by the binary system forms a specific physical situation, where a general relativity can be seriously confronted with the source theory of gravity. This article is an extended version of an older article by the present author Pardy, in which only the spectral formulas were derived. Here we have derived the quantum energy-loss formulas, with no specific assumption concerning the strength of the gravitational field. We hope that future astrophysical observations will confirm the quantum version of the energy loss of the binary black hole and galaxy binary. There is the fundamental problem concerning the maximal mass of the black hole and galaxy. The theory of the space-time with maximal acceleration constant was derived by author. In this theory the maximal acceleration constant is the analogue of the maximal velocity in special theory of relativity. Maximal acceleration, determines the maximal black hole mass where the mass of the black hole is restricted by maximal acceleration of a body falling in the gravity field of the black hole. Conclusion The another question is what is the relation of our formulas to the results obtained by LIGO-the Laser Interferometer Gravitational-Wave Observatory. LIGO is the largest and most sensitive interferometer facility ever built. It has been periodically upgraded to increase its sensitivity. The most recent upgrade, Advanced LIGO, detected for the first time the gravitational wave, with sensitivity far above the background noise. The event with number GW150914, was identified with the result of a merger of two black holes at a distance of about 400 Mpc from Earth LIGO. Two additional, significant detections, GW151226 and GW170104, were reported later. We can say that at this time it is not clear if the LIGO results involves information on the spectrum of gravitons calculated in this chapter. References 1. Acernese F, Agathos M, Agatsuma K, et al. Advanced Virgo: A second-generation interferometric gravitational wave detector. Class Quantum Gravity. 2014;32(2):024001. 2. Blanchet L. Gravitational radiation from post-Newtonian sources and inspiralling compact binaries. Living Rev Relativ. 2014;17(1):2. 3. Buonanno A, Damour T. Effective one-body approach to general relativistic two-body dynamics. Phys Rev D. 1999;59(8):084006. 4. Bolton CT. Dimensions of the binary system HDE 226868=Cygnus X-1. Nat Phys Sci. 1972;240(102): 124-127. 5. Campanelli M, Lousto CO, Marronetti P, et al. Accurate evolutions of orbiting black-hole binaries without excision. Phys Rev Lett. 2006;96(11):111101. 6. Casares J, Jonker PG. Mass measurements of stellar and intermediate-mass black holes. Space Sci Rev. 2014;183:223- 252. 7. Damour T, Taylor JH. Strong-field tests of relativistic gravity and binary pulsars. Phys Rev D Part Fields. www.tsijournals.com | June-2025 11 1992;45(6):1840. 8. Dittrich W. Source methods in quantum field theory. Fortschritte Der Physik. 1978:26(5);289-356. 9. Finkelstein D. Past-future asymmetry of the gravitational field of a point particle. Phys Rev. 1958;110(4):965. 10. Gold T. Rotating neutron stars as the origin of the pulsating radio sources. Nature. 1968;218(5143):731-732
