Original Article
, Volume: 6( 1)Probability as a Field Theory
- *Correspondence:
- Solomon BT A Chairman, Xodus One Foundation, 815 N Sherman St., Denver, CO 80203, USA
Tel: 3106663553; E-mail: bts@XodusOneFoundation.org
Received: December 06, 2016 Accepted: April 03, 2017 Published: April 06, 2017
Citation: Solomon BT, Beckwith AW. Probability as a Field Theory. J Space Explor. 2017;6(1):117.
Abstract
A review of quantum theory shows that quantum theory has substantially replaced all photon behaviour with wave equations. This therefore, has resulted in a quantum theory that does not have a mechanism to explain how Nature implements probabilities. The proposal for such a mechanism is divided into 3 parts of which this paper is the third. The papers [2] and [6] are the first and second parts. This paper proposes a basic field theory for probabilities, which is derived from a step by step analysis of the Point Spread Function of photon localizations. By deconstructing probabilities to separate out the wave modulation from the underlying probabilities it is possible to determine that the photon energy is the cause of the probability field that surrounds the photon. Further, the classical definition of probabilities is used to derive a physical definition of probabilities. From this is derived the correct or true mechanism of the probability field, that of location transfer or translocation, and some addition thoughts on Bell’s Theorem.
Keywords
Airy Pattern; Bell’s theorem; Electron shell; Photon localization; Photon probability; Photon propagation; Probability; Schrödinger wave function
Introduction
Quantum theoretic approach
Quantum theory [1] describes both mass-based particles and massless particles as wave functions only, to the extent that all photon behaviour are expressed as wave functions. Even probabilistic properties are expressed as wave functions. Solomon and Beckwith [2], however, showed that an alternate probabilistic description is feasible. The point spread function (PSF), here termed Airy Pattern, of photons projected through a pin hole to a screen, is the basis of this alternate probabilistic description.
Further, there is in physics research, what is known as the pilot model [3], which has a specific re-interpretation of probability, and not just on the basis of wave interference. “The Copenhagen interpretation is essentially the assertion that in the quantum realm, there is no description deeper than the statistical one. When a measurement is made on a quantum particle, and the wave form collapses, the determinate state that the particle assumes is totally random. According to the Copenhagen interpretation, the statistics don’t just describe the reality; they are the reality” [4].
The research in this paper is to determine another layer of statistical inference, as an alternative to the Copenhagen interpretation, and that is what the offered aim of this paper is.
Deconstructing probability without wave modulation
For the sake of clarity and ease of reading this paper, this section is taken from §3 of Solomon and Beckwith [5]. Roychoudhuri [6] points out that quantum electrodynamics assigns rich properties to “vacuum” and yet relativity and quantum physics do not explicitly recognize space as a real physical medium. Solomon and Beckwith [2] had proposed that subspace (x, y, z) is how Nature implements probabilities. It was proposed [2,7,8] that electric and magnetic field energies are transferred to subspace as these field energies not conserved within the transverse wave. Just as gravitational fields have a time invariant potential energy structure in spacetime, observed as spacetime curvature, the transverse wave’s electric and magnetic field energies transform the structure of subspace curvature to exhibit probability density per C (3).
Gravitational fields have several important properties, (i) a source, or mass and (ii) a field structure, or curvature, (iii) the field effect, gravitational acceleration, is due to field curvature (iv) total field strength, and (v) the total field energy dependent upon the amount of the gravitating mass [9,10].
Using this gravitational model as an analogy, this paper proposes (i) the source of a photon’s probability density is the transverse wave’s electric and magnetic field energies, (ii) the observed subspace curvature is the inverse radial function per C(3), (iii) the field effect, probabilities, is due to the subspace curvature, (iv) the total field strength is the total probability density function PψP per C(5), and (v) the total probability density is dependent upon the total electric and magnetic field energy.
Per (i), using the electric field energy TηE, to keep it simple,
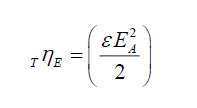 (1)
(1)
Per (ii), from C (3),
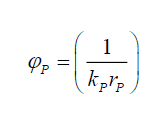 (2)
(2)
Per (iii), from C (4),
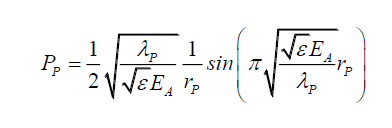 (3)
(3)
In the absence of the transverse wave’s modulation of the probabilities,
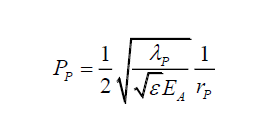 (4)
(4)
Per (iv), from C (5) and C (4),
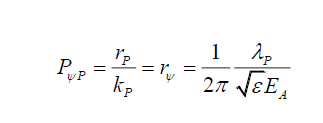 (5)
(5)
And from (12) and C (19),
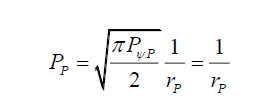 (6)
(6)
That is, in the absence of any wave modulation, photon probability is purely an inverse function of the radial distance rP from axis of motion. That is, per Solomon and Beckwith [11-15], just as wave equations and probabilities are different phenomena, given a consistent particle structure, it is possible to define probabilities in terms of the wave equations.
Per (v), the relationship (1) between source and field is proposed by equating the total electric field energy (electric field energy density TηE x volume VE occupied by this electric field) to probability density PψP (because the electric field is that of the transverse wave, the probability density PψP in the plane of this transverse wave is the equivalent). However, by C (19) and (5)
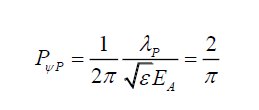 (7)
(7)
Or
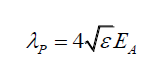 (8)
(8)
Or
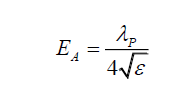 (9)
(9)
Thus, the electric field strength EA, of the transverse wave is purely a function of it wavelength and the electric permittivity of the environment, and as the photon’s wavelength λP increases it electric field strength EA also increases. That is, there is no standard electric field strength EA for the photon.
Rewriting, gives, the electric energy density ηE in terms of the photon wavelength λP, and photon energy EP,
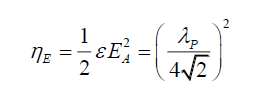 (10)
(10)
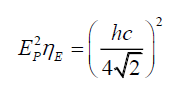 (11)
(11)
The electric field energy density ηE is a function of the square of the photon’s wavelength λP. As the right had side of (11) is a constant, one infers that the electric field energy density is like a store, transmuting into photon energy EP per (11), and it is independent of photon wavelength λP.
Thus, (a) photons total probability density functions PψP C(9) and DψP C(10) evaluate to a constant and is independent of its wavelength λP (b) their electric field energy densities and photon energies are interchangeable and governed by (11), (c) as EP → ∞ , ηE → 0 and photons lose their wave characteristics and appear to be point-like particles, (d) at this stage it is not possible to equate the photon probability density functions to their energies as (7) shows how electric field and wavelength compensate for each other, (e) this section forms the basis of a field theory approach to how probabilities are implemented in Nature.
From C (21) and (8), the photon probability in the absence of any other external factors, can be rewritten as,
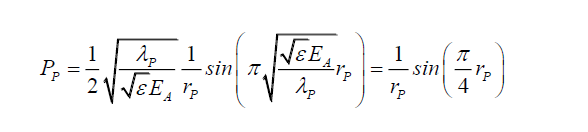 (12)
(12)
Therefore, the non-modulated, without the effect of the space wave, probability PN takes the form,
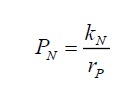 (13)
(13)
Where kN is some constant. That is one now has a probability function (13) that is deconstructed from the modulated probability function (12). Note that (6) informs the shape of the probability function at any distance rP, while C (9) or PψP and C (10) DψP, provide the total value of the respective photon probability density functions, but not their shapes. Therefore, to develop a probability field theory, the next step is to answer the question, what is the shape of the photon’s non-modulated probability density function ψN given its probability function PN?
Interpretation and definitions of probability and probability density
Starting with the premise that the photon probability modulation is due to the space wave χP C (2), it is necessary to determine the true relationship of probabilities in the absence of this modulation. Rewriting B (13) and C (10) in the form of a straight line (14),
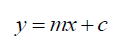 (14)
(14)
one gets,
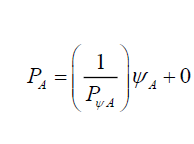 (15)
(15)
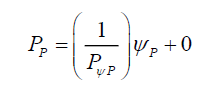 (16)
(16)
That is, conceptually probability relationships can be structured into three parts, (i) probability PA or PP is the y effect function, (ii) caused by the probability density ψA or ψP, the x-source function (iii) whose effects is modified by the total probability density 1/PψA or 1/PψP the m gradient function or in general using a generic process D,
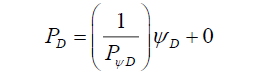 (17)
(17)
One can now define probabilities in terms of spatial properties. The classical definition of probabilities is that, for a given process, probability is the ratio of the number of outcomes of a specific event over the total number of outcomes of all possible events. From this classical definition one can now propose a physical definition of probability.
The physical probability PF field is defined as the field in which is evidenced latent or real localization events caused by the localization probability density function ψD. Such that, the probability PD at a point SD from a reference point SR is the occurrence of localization events at SD over the total number of localization events caused by the total localization probability density function PψD from that same reference point SR within range defined by its range of upper point SU and lower point SL, in a time invariant manner.
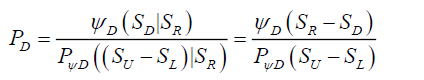 (18)
(18)
In terms of (18), (15) and (16), are rewritten as (19) and (20), respectively,
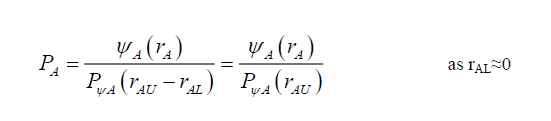 (19)
(19)
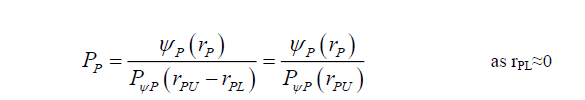 (20)
(20)
Therefore, the non-modulated photon probability PN is the direct effect of the photon’s non-modulated probability density function ψN,
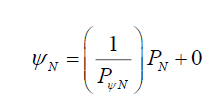 (21)
(21)
Since, the range of rP determines the photon’s probability range C (13), and by C(21) that the oscillating electric field EA (22) alters the photon’s probability,
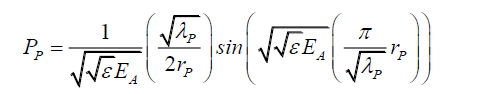 (22)
(22)
As probabilities, cannot be negative, the magnitude of the photon probability due to the oscillations is,
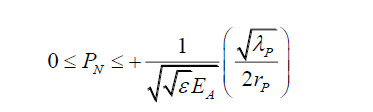 (23)
(23)
And therefore, the governing relationship with the maximum electric field amplitude EA is, (24)
Since, the wavelength λP is a constant for a given photon,
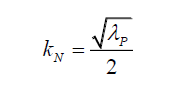 (25)
(25)
And,
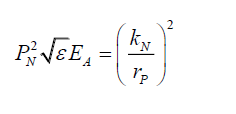 (26)
(26)
Or,
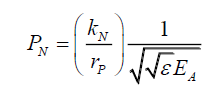 (27)
(27)
Or because PψN is a constant, grouping all the constant terms, by (21) one can propose that,
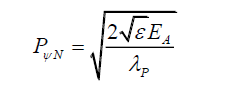 (28)
(28)
And,
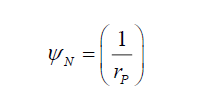 (29)
(29)
Thus, the total probability density function PψN is a function of the photon’s electric field and its energy. (29) informs of the shape of the non-modulated probability density function ψN. The non-modulated probability PN is given by,
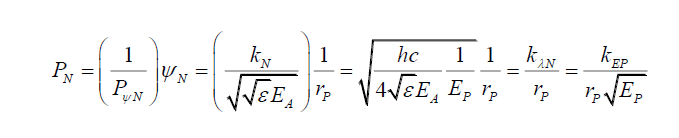 (30)
(30)
And kλN and kEP are some constants as rP is the only variable for a specific photon wavelength λP.
Probability as an energy deformation of space
With this information and noting that the probability field is a disc (x-y axes) orthogonal to the field of motion (z-axis), (30) can be rewritten along the x-axis as,
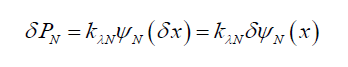 (31)
(31)
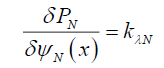 (32)
(32)
Or in the limit as x→0,
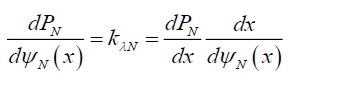 (33)
(33)
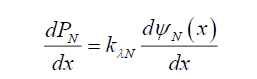 (34)
(34)
Similarly, along the y-axis,
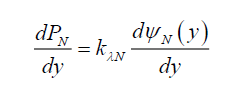 (35)
(35)
Developing the probability field PFtheory with reference to Appendix C, it is noted that the probability field does not cause localizations [2]. Localizations are due to the spacetime-subspace αβ joins. A probability field on the other hand is a region of space (not spacetime as the probability field is time invariant) that determines how likely a localization event L(rP) a distance rP from the reference point SR (in this case the axis of the photon motion) is likely to occur given a spacetime-subspace αβ join is present at rP. Note, there may be more than one spacetime-subspace αβ joins present within the probability field PF.
Using (30), the total probability PT, with radius rP set at its maximum value rPL over the photon’s probability disc must be 1, from C (4) and C (17),
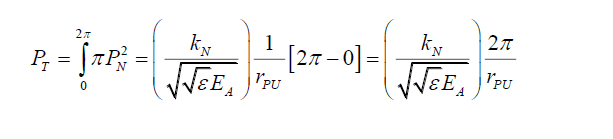 (36)
(36)
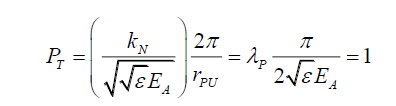 (37)
(37)
Or for the total probability disc, as opposed to the radial probability, the relationship between wavelength and electric field strength is given by,
 (38)
(38)
But from (8),
 (39)
(39)
One would have thought that the relationship between wavelength and electric field would have been the same. It is suggested that (39) be used when determining the electric field amplitude of a single photon and (38) be used when modifying the photon’s total probability field.
Using (34) and (35) one can now rewrite subspace deformation in terms of this photon energy. Considering a 1-dimensional formulation, along the orthogonal x-axis,
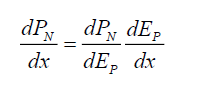 (40)
(40)
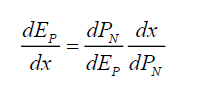 (41)
(41)
From (30), for a specific photon wavelength,
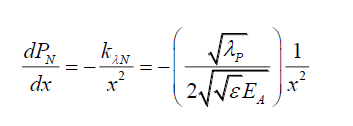 (42)
(42)
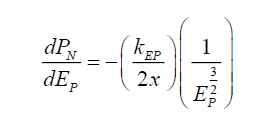 (43)
(43)
Therefore, the subspace gradient of the photon energy in 1-dimension is given by,
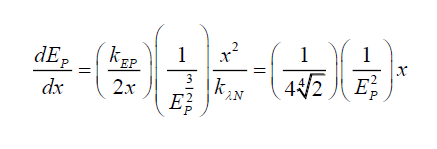 (44)
(44)
Or, the 1-dimensional deformation of subspace by this photon energy is given by,
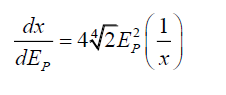 (45)
(45)
Note, however, this is not a useful approach as (44) is the spatial photon energy gradient along a radial axis, and does not provide how photon energy stresses the space. To do that one needs to consider the change in probabilities as a result of a change in the photon energy. From (30), given two photons 1 and 2 with EP1 and EP2 energies, probabilities PN1 and PN2 and maximum electric field amplitudes EA1 and EA2 respectively, at a distance rP from the z-axis are given by,
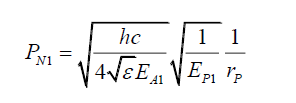 (46)
(46)
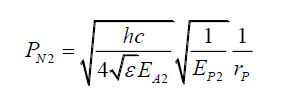 (47)
(47)
Assuming that EA1 ≈ EA2 for simplicity,
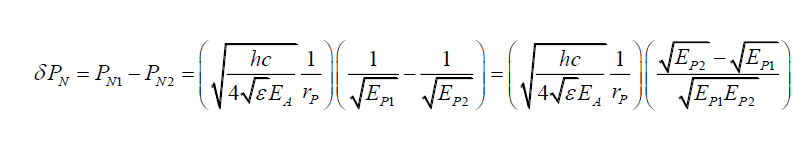 (48)
(48)
And as EP2 → EP1, EP2 → EP1 +δEP thus,
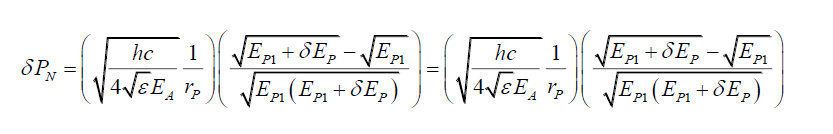 (49)
(49)
Using two simplifying assumptions,
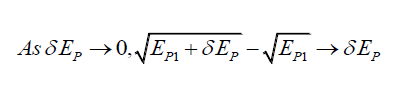 (50)
(50)
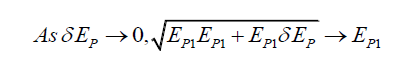 (51)
(51)
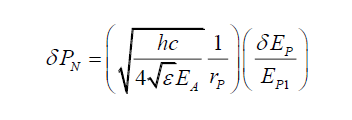 (52)
(52)
Or,
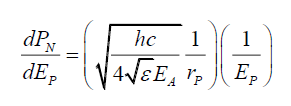 (53)
(53)
(53) is the probability energy gradient, or how probabilities change if the photon energy is changed. Therefore, integrating (53) with respect to EP gives,
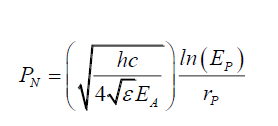 (54)
(54)
(54) is the relationship between probabilities and photon energy, or the physical manifestation of the probability field PF is the spread of photon energy across the disc such that the amount of photon energy present at a spacetime-subspace αβ joins is equivalent to its probability PN. Therefore, photons do not mysteriously localize at a point orthogonal to their motion. Their energy is spread over the disc and therefore, some portion of the photon is already present at the point where they localize.
What is the probability field PF?
To develop a field theory for probabilities requires an understanding of what the probability field PF is? Both the classical and physical definitions of probabilities provide descriptions of, but do not answer this question. From the physical description, one notes that the probability field PF is a mechanism to relocate a photon’s position, given localization events. Thus, this probability field PF is a location transfer or translocation mechanism. This translocation is instantaneous as the field is time invariant, and therefore not related to motion or Lorentz-FitzGerald Transformations (LFT). The instantaneous nature of the PF probability field’s translocation mechanism points to a photon energy that is rich or sophisticated [16].
Rewriting (30) from the perspective of translocation gives,
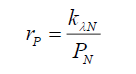 (55)
(55)
That is, the radial distance translocated is inversely proportional to its probability. Noting that the photon’s disc (see Appendix C) has a range per (56),
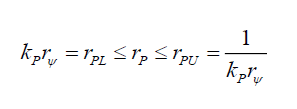 (56)
(56)
Integrating (44), gives
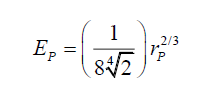 (57)
(57)
Therefore, the total photon energy EPr within the disc formed by the radius rP is,
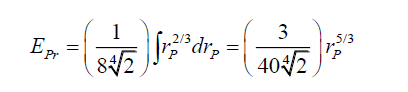 (58)
(58)
(58) determines the cumulative photon energy at the radius rP. There is a monotonic relationship between the translocation distance rP and the photon energy EP to get to that distance. Or, the greater the proportion of the photon energy EP within a radius rP the greater is the translocation distance rP.
Is the gravitational field mechanism the same as that of the probability field? No. The gravitational field is constrained by the Lorentz-FitzGerald Transformation (LFT) while the probability field is not.
What about Bell’s theorem?
Khrennikov [17] stated “Bell's theorem rejects only local hidden variable models, i.e., models preventing faster than light communications.” Bell’s theorem is limited to spacetime. However, as shown [2], the conservation of energy within the electromagnetic transverse wave requires both the existence of the spacetime (x,y,z,t) and subspace (x,y,z). Subspace does not have the time dimension. In this light Bell’s theorem in a richer spacetime (per Roychoudhri’s critique [5]) is inapplicable for two reasons,
• Bell’s theorem assumes that spacetime is not rich. Therefore, the disproof of hidden variables only disproves traveling hidden variables. The implicit assumption in Bell’s theorem is that velocity is the only mechanism for the conveyance of signals between entangled photons.
• In a rich spacetime, other mechanisms for the conveyance of signals are possible. Solomon and Beckwith [6] proposed an experimental test that could determine if entanglement could either be due to probabilities or due to subspace itself. Therefore, there are two more signal conveyance mechanisms,
• Probabilities as subspace structures do not travel but are photon energy structures that exists over a large radius, and therefore a possible mechanism for probabilistic hidden variables.
• Subspace itself could be another mechanism as it does not have the time dimension, and therefore the conveyance mechanism would be space hidden variables.
Therefore, this exploration of how probabilities are implemented in Nature, partially invalidates Bell’s Theorem.
Conclusion
This paper has laid the foundations of a field theory for probabilities, by starting with the premise that photon energy within the transverse electromagnetic wave must be conserved at any and every instance within this wave. This requires the existence of a subspace that is time invariant and therefore a suitable candidate for how Nature implements probabilities. In developing a field theory for probabilities this paper proposed that there isn’t a standard electric field strength associated with the electromagnetic wave. By proposing a rich 4-dimensional spacetime (x, y, z, t) it is possible to derive a basic field theory for photon probabilities that is dependent upon photon energy. This leads to the inference that probability is a location transfer or translocation mechanism.
References
- Wong CW. A review of quantum mechanics, review notes prepared for students of an undergraduate course in quantum mechanics. Department of Physics and Astronomy, University of California, Los Angeles, CA2006;2016.
- Solomon BT, Beckwith AW. Probability, randomness and subspace, with experiments. J Space Explor. 2017;6(1).
- Bohm D. "A Suggested Interpretation of the Quantum Theory in Terms of Hidden Variables, II". Phys. Rev. 1952; 85(2):180-193.
- Massachusetts Institute of Technology [internet]. Fluid mechanics suggests alternative to quantum orthodoxy [cited on Sep 12, 2104]. Available from: [ttp://news.mit.edu/2014/fluid-systems-quantum-mechanics-0912]
- Solomon BT, Beckwith AW. Photon Probability Control with Experiments. J Space Explor. 2017;6(1).
- Roychoudhuri C. Causal Physics: Photons by non-interactions of waves, CRC Press, Boca Raton; 2014.
- Solomon BT. Non-gaussian photon probability distributions, in the proceedings of the space, propulsion and energy sciences international forum (SPESIF-10). Glen AR, editors. AIP Conference Proceedings 1208; Melville, New York; 2010.
- Solomon BT. Super physics for super technologies: Replacing Bohr, Heisenberg, Schrödinger and Einstein, Propulsion Physics Inc, Denver March; 2015.
- Efstathiou G, Pryke C, Steinhardt P, et al. Spotlight live: Looking back in time-oldest light in existence offers insight into the universe. The Kavli Foundation; 2015.
- Nemiroff R. Bounds on spectral dispersion from fer-mi-detected gamma ray bursts. Phys Rev Lett. 2012;108:231103.
- Solomon BT. New evidence, conditions, instruments and experiments for gravitational theories. J Mod Phys. 2013;4:183-96.
- Solomon BT. Empirical evidence suggest a need for a different gravitational theory, American Physical Society (APS) April Conference, Denver; 2013.
- Solomon BT. An introduction to gravity modification: A guide to using Laithwaite's and Podkletnov's experiments and the physics of forces for empirical results. 2nd ed, Universal Publishers, Boca Raton, Edition; 2012.
- Solomon BT. Gravitational acceleration without mass and non-inertia fields. Phys Essays. 2011;24: 327.
- Solomon BT. An approach to gravity modification as a propulsion technology, in the proceedings of the space, propulsion and energy sciences international forum (SPESIF-09). Glen AR, editors. AIP Conference Proceedings 1103; Melville, New York; 2009.
- Hooft G. A locally finite model for gravity. Found Phys. 2008;38:733-57.
- Khrennikov A. Randomness: Quantum Versus Classical”. Quantum Physics; 2015.

