Original Article
, Volume: 6( 3)Probabilistic Deformation in a Gravitational Field
- *Correspondence:
- Solomon BT, Chairman, Xodus One Foundation, 815 N Sherman St., Denver, CO 80203, USA, Tel: 310-666-3553; E-mail: bts@XodusOneFoundation.org
Received: September 09, 2017; Accepted: September 25, 2017; Published: September 30, 2017
Citation: Solomon BT, Beckwith AW. Probabilistic Deformation in a Gravitational Field. J Space Explor. 2017;6(3):130
Abstract
This paper proposes the Center of Field method to determine the bending of the photon’s path in a gravitational field. The numerical model developed, shows that this bending is independent of the energy of the photon and therefore, it probability. This informs of possible particle structure. Further, as the authors’ research is primarily focused on developing interstellar propulsion physics and technologies, these finding would suggest that navigation systems for interstellar propulsion would necessarily need to account for gravitational fields. Finally, this paper reviews a key Schrödinger axiom.
Keywords
Gravitational constant; Bending of light; Probabilistic wave function.
Introduction
In 2015, Esftathiou et al. [1] stated that the Planck Space Telescope data shows that the Universe is simpler than had been thought and that both string and quantum theories require revisions. To add to this debate, in 2012 using Fermi gamma-ray space telescope photographs of gamma ray burst, Nemiroff [2] showed that quantum foam could not exist. A year later, 2013, Solomon [3] proposed that both exotic matter and strings could not exist and in 2010 [4] and 2015 [5].
Solomon had proposed that photon probability could not be Gaussian. Subsequently, Solomon [5,6] and Solomon and Beckwith [7-10] presented an approach to rewriting the foundations of physics that is based on and vindicated by the empirical data. That, given that the photon probability can be described by the Probabilistic Wave Function ψP (1) and its components the space wave χP (2) and the envelope probability density function φP (3),
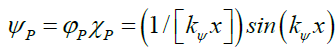 (1)
(1)
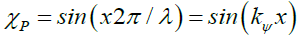 (2)
(2)
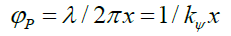 (3)
(3)
Experimental
Solomon [5,6] proposed a Center of Field CF as an alternative to quantum theory’s force carrier particles which essentially states that the particle as a field observes a deformation of the field’s shape. This results in the shift in the Center of Field CF and is evidenced as acceleration. For example, in a gravitational field, the massless formula for gravitational acceleration (4) is derived from the Center of Field CF as,
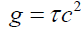 (4)
(4)
Where, τ is the spatial gradient of the time dilation transformation or change in time dilation transformation divided by that distance and noting that the time dilation transformation is the ratio of tv/t0 per Lorentz-FitzGerald Transformation LFT (5) and Newtonian Gravitational Transformations NGT (6).
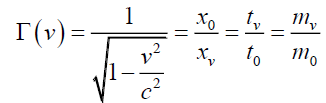 (5)
(5)
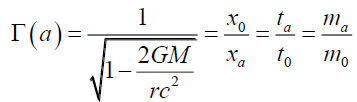 (6)
(6)
The particle’s Center of Field CF in a gravitational field is governed by the shift in the center of mass for gravitational acceleration. The center of mass CM0 of a particle at rest is given by,
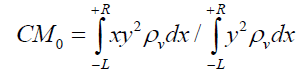 (7)
(7)
In a gravitational field Φ the moments MΦi of the mass mΦi of slice i with a non-linear mass density behavior ρΦi (8) and the particle’s center of mass CMΦ (7) in the gravitational field Φ is given by equation (9). This is the standard center of mass equation (9) modified to handle the non-linearity introduced by gravitational spacetime deformation.
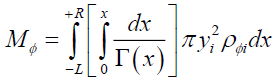 (8)
(8)
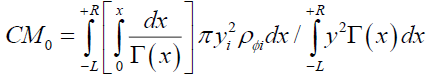 (9)
(9)
Where,
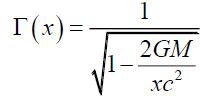 (10)
(10)
Note that the gravitational gradient is implemented by equation (10) and that (9) does not have an analytical solution. To derive an elegant solution a numerical integration model was used to construct the shape and mass of a gravitationally deformed particle by slicing it into 2,000 disc-shaped slices, with 1,000 slices on each side of the particle in relation to its center and the gravitational source. The moments of each slice were calculated to determine the new center of mass. The mass msi of a slice i a distance, xi, from its center and r from the gravitational source, with density ρi and thickness qi is given by equation (11). Mass density ρi and thickness qi of slice i are determined by Γ(a) equation (12). The distance of the center of the ith disk from the center of particle is the summation of the thickness of all previous disks, from 1 to i-1, plus half of the ith disk, given by equation (13). Therefore, the numerical formulation for the center of mass CM for a shape function y is given by equation (14).
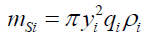 (11)
(11)
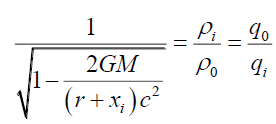 (12)
(12)
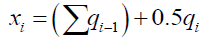 (13)
(13)
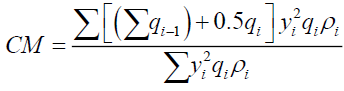 (14)
(14)
To test for effects of particle shape and mass distribution 1,190 numerical integrations were evaluated for 7 particles sizes from 10-21 m, smaller than an electron, up to 10-3 m, a small pin head; modelled in 10 gravitational fields, with 17 shapes or mass distributions. The results of these extensive numerical modeling give three simple equations (i) the gravitational acceleration g is governed by the change in center of mass χ (15) where kd is some constant, (ii) the change in the center of mass χ of a particle (16) is a function of the change in time dilation δt across the particle for a specific particle size Sz. And (iii) one notes that the two constant terms kd and km are sufficient to parameterize any shape or mass distribution of a particle. The numerical value of kc is within 0.049% of the numerical value of the square of the velocity of light c2 or 8.9875517873681764 × 10+16. Since Sz is the change in the distance δr from the gravitational source, in the limit as δr→0, equation (17) becomes equation (18) where τ=dt/dr.
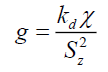 (15)
(15)
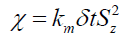 (16)
(16)
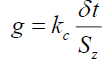 (17)
(17)
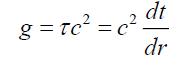 (18)
(18)
These findings strongly suggest that the Centre of Field CF approach is how nature implements field interactions in general and forces in particular.
Probabilistic deformation
Einstein had proposed [11] that light bends α degrees, in a gravitational field (19), whose mass is M and of radius r.
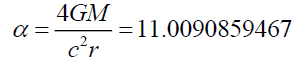 (19)
(19)
Or
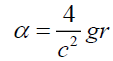 (20)
(20)
Obviously [12], (19) is an approximation as the observed experimental evidence at the Sun is,
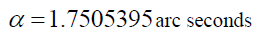 (21)
(21)
Or a correction factor kcor, required for the approximation (19) is
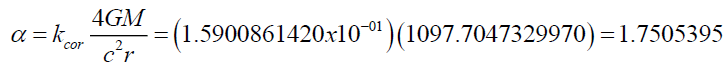 (22)
(22)
Or the gravitational acceleration experienced by a deflecting photon at the surface of the Sun is,
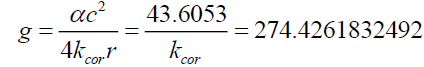 (23)
(23)
With the correction factor kcor, (23) compares well with the calculated value of the Sun’s gravitational acceleration of 273.9672 m/s2.
The probabilistic deformation in local spacetime of the gravitational field provides an opportunity to falsify (technical term) General Theory Relativity GTR. Since gravity permeates all particles, Solomon [6], per (24) as the transformations in spacetime Γs(x,y,z,t) are mirrored in the particle ΓP(x,y,z,t),
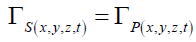 (24)
(24)
it is acceptable to propose that in the absence of all other factors, the transformation a probability field experiences in a gravitational field is identical to that of other particle fields. Per the discussion in the previous section, one can now use the Center of Field CF approach to modeling probabilistic deformations.
Reverting to (9) as the basis of determining probabilistic deformation in a gravitational field and modeling an infinitely thin probability disc, Probabilistic Wave Function per Solomon and Beckwith [7,8,9] of a photon travelling tangentially to the radius of the gravitational field, gives the following formulations,
• Given the radial distance ri,j from the center of the photon,
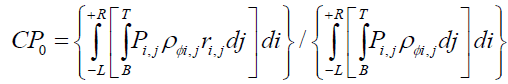 (25)
(25)
• The probabilistic energy density ρ?i,j at a point (i, j) on the disc at a distance rPi,j form the center of the gravitational field,
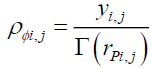 (26)
(26)
• The y probability function determined by the Probabilistic Wave Function per Solomon and Beckwith [7,8,9] and is given by (26)
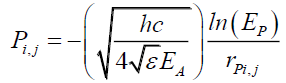 (27)
(27)
And can be rewritten in terms of the photon energy EP as, Solomon and Beckwith [9],
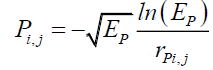 (28)
(28)
• The center of the photon probability field CP0, for i between a distance -L (left) R (right)
• L ≤ i ≤ R with the gravitational source to the left of the photon (29)
• B ≤ j ≤ T for j between a distance -B (bottom) to T (top) (30)
• Note that radial distance ri,j from the centre of the photon is contracted per NGT.
As (24) is not integrable, solving (24) to derive an elegant solution requires a numerical integration model. This numerical integration Center of Field CF [5 and 6] model results, developed for a gravitational field, are presented in Table 1. This numerical model consisted of 7,845 points within the photon’s probability field (27) and due to the X-Numbers MS Excel limitations of 256 columns; the radius of this probability disc was limited to 200 m (i.e. 200 columns).
| Gravitational space time | Flat space time | |||||
|---|---|---|---|---|---|---|
| Index | Color | Wavelength (m) | CP0 | Average probability | CP0 | Average probability |
| 1 | Violet | 4.00E-07 | 3.6342983332E-12 | 2.2355977123E-06 | 1.500E-247 | 1.9536062812E-06 |
| 2 | Indigo | 4.45E-07 | 3.6342983332E-12 | 2.1249113185E-06 | 2.200E-247 | 1.8568815290E-06 |
| 3 | Blue | 4.75E-07 | 3.6342983332E-12 | 2.0598901556E-06 | 2.900E-247 | 1.8000619358E-06 |
| 4 | Green | 5.10E-07 | 3.6342983332E-12 | 1.9912912847E-06 | 2.700E-247 | 1.7401159158E-06 |
| 5 | Yellow | 5.70E-07 | 3.6342983332E-12 | 1.8885152943E-06 | 2.500E-247 | 1.6503037730E-06 |
| 6 | Orange | 5.90E-07 | 3.6342983332E-12 | 1.8577367983E-06 | 1.900E-247 | 1.6234075820E-06 |
| 7 | Red | 6.50E-07 | 3.6342983332E-12 | 1.7739494837E-06 | 1.500E-247 | 1.5501889418E-06 |
Table 1: CF shift of photon without wave function modulation.
The numerical model results show that, even though the photon energy changes, the shift in the center of the probability field CP0 is constant. Like mass particles whose acceleration is independent of mass, the shift in the CP0 is independent of photon energy (even though photon energy is present in the model), which is a mass equivalent and in agreement with (23) i.e. not a function of photon energy.
One can solve for the constant term in (16), given the model results,
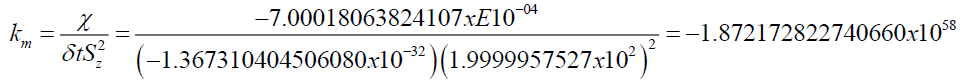 (31)
(31)
Note, that since the photon’s Probabilistic Wave Function radius is very large, δt and Sz are taken to be very small increments at the photon axis of propagation, where δt is the change in LFT. And therefore, kd (15) is given by [6],
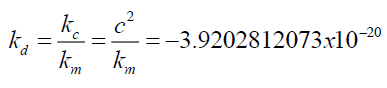 (32)
(32)
By (18) and since (18) is for mass particles, inserting an adjusting constant term kg and kg’,
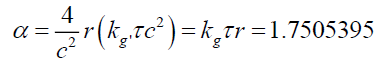 (33)
(33)
Solving for kg in arc seconds gives,
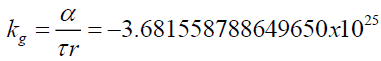 (34)
(34)
The bending of light in a gravitational field is no longer a function of the gravitating mass source but that of the properties of the local spacetime in which it propagates. That is, it is a local phenomenon.
So far the modeling of photon probability without the wave functions. Adding back the wave function, Solomon and Beckwith [9] using (33), where rp is the distance from the center of the photon,
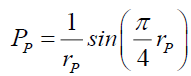 (12), from [9] (35)
(12), from [9] (35)
The photon probability Pi,j at any point i, j is,
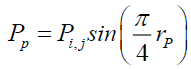 (36)
(36)
Solving for the constant term in (16) given the same model results as in (31), (32) and (34). That is the constant terms, km, kd and kg are identical whether the photon’s wave modulation is present or not.
The minus sign for the probabilities in Tables 2 and 3 are due to the negative sign of the photon’s electric field vectors. This is the same interpretation Dirac provided [13] that energy cannot be negative and therefore, the negative sign is to be interpreted as an opposite electric charge, thereby discovering antiparticles.
| Gravitational space time | Flat space time | |||||
|---|---|---|---|---|---|---|
| Index | Color | Wavelength (nm) | CP0 | Average probability | CP0 | Average probability |
| 1 | Violet | 4.00E-07 | -7.0001806382E-04 | -3.5644076001E-08 | 3.400E-247 | 3.5644100593E-08 |
| 2 | Indigo | 4.45E-07 | -7.0001806382E-04 | -3.3879306690E-08 | 4.700E-247 | 3.3879330060E-08 |
| 3 | Blue | 4.75E-07 | -7.0001806382E-04 | -3.2842617818E-08 | 4.800E-247 | 3.2842640470E-08 |
| 4 | Green | 5.10E-07 | -7.0001806382E-04 | -3.1748886440E-08 | 9.700E-247 | 3.1748908335E-08 |
| 5 | Yellow | 5.70E-07 | -7.0001806382E-04 | -3.0110239561E-08 | 7.200E-247 | 3.0110260322E-08 |
| 6 | Orange | 5.90E-07 | -7.0001806382E-04 | -2.9619511268E-08 | 1.000E-247 | 2.9619531689E-08 |
| 7 | Red | 6.50E-07 | -7.0001806382E-04 | -2.8283617339E-08 | 7.300E-247 | 2.8283636837E-08 |
Table 2: CF shift for photon with wave function modulation.
| (For yellow light photons of wavelength 5.70 nm) | ||||||
|---|---|---|---|---|---|---|
| Average probability | ||||||
| Index | Mass of Sun (kg) | Near side | Far side | Difference | Probability, flat space time |
CP0 |
| 1 | 1.99E+30 | -3.0110239561E-08 | -3.0110239561E-08 | 5.8941124900E-21 | 3.0110260322E-08 | -7.0001806382E-04 |
| 2 | 1.99E+31 | -3.0110021770E-08 | -3.0110021770E-08 | 6.2815746232E-20 | 3.0110260322E-08 | -7.0000383882E-04 |
| 3 | 1.99E+32 | -3.0104779315E-08 | -3.0104779316E-08 | 1.0158514594E-18 | 3.0110260322E-08 | -6.9989267113E-04 |
| 4 | 1.99E+33 | -2.9745329898E-08 | -2.9745329947E-08 | 4.8982491887E-17 | 3.0110260322E-08 | -7.0193436751E-04 |
Note: The apparent increase in fourth CP0 is due to the graininess of the Excel model.
Table 3: Probability deformation vs. gravitational mass.
Results and Discussion
Modeling inferences
The numerical modeling results, Tables 1 and 2, show that the gravitational acceleration on a photon is independent of photon energy even though it does deform the photon’s probability field. This is equivalent to gravitational acceleration independent of the mass of mass-particles even though mass is deformed by NGT across the particle. That is the concept of the spacetime continuum is falsifiable. The second point worth noting is that photons are not refracted by the gravitational field. This is evidenced by the ALMA photograph [14] which does not show diffraction fringe patterns, that a different mechanism, probabilistic deformation using the Center of Field method, explains why Einstein [11] and Putoff [12] proposed a refraction or polarizability mechanism for gravitational fields, respectively.
Table 3. shows how probabilities are affected as the mass of the Sun is increased while keeping its radius constant. The photon probabilities decrease with gravitational strength and shifts towards the far side of the gravitational source. This would suggest that more photons are observed from black hole than if one assumed that probabilities are not altered by gravitational fields, as more photon interactions are likely on the far side than the near side. Also, compared to probabilities in flat spacetime, gravitationally distorted probabilities are less than those in non-gravitational spacetime.
Further testing, Table 4 shows that km is not stable as the gravitating mass increases. Regressing (R2 = 99.85%) gives,
| Index | Mass of Star (kg) | km | Ln (mass) | Ln (km) |
|---|---|---|---|---|
| 1 | 1.99E+30 | 1.1421933938E+18 | 6.9765235065E+01 | 4.1579482117E+01 |
| 2 | 1.99E+31 | 1.1421918167E+17 | 7.2067820158E+01 | 3.9276895644E+01 |
| 3 | 1.99E+32 | 1.1422268183E+16 | 7.4370405251E+01 | 3.6974341194E+01 |
| 4 | 1.99E+33 | 1.1477386331E+15 | 7.6672990344E+01 | 3.4676569995E+01 |
| 5 | 1.99E+35 | 2.7286301910E+13 | 8.1278160530E+01 | 3.0937405931E+01 |
Table 4: km vs. Gravitational mass.
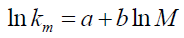 (37)
(37)
where a and b are constants, given by,
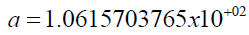 (38)
(38)
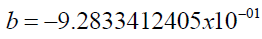 (39)
(39)
Since this research pursues an approach to interstellar propulsion using probabilities that bypass LFT and NGT, it would suggest that gravitational fields can alter translocation [9] based interstellar navigation systems.
Testing for the variability of the gravitational constant, G
Solomon [5] and Solomon and Beckwith [10] had proposed that the gravitational constant G was not a constant Gi but changes with the mass of isotope i. Therefore, the gravitational constant G is a composite (40) of the isotopic gravitational constants Gi (41) of element i and is dependent upon the isotopic mass Mi (38) of element i.
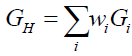 (40)
(40)
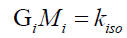 (41)
(41)
Where isotope constant, kiso = 2.973856 × 10-36 m3s-2 and wi is the proportion of that isotope I in the gravitating mass. Thus the gravitational acceleration of a heavenly body H of mass MH and radius RH is given by (42),
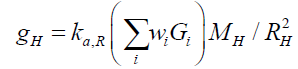 (42)
(42)
Where gH is the gravitational acceleration of a heavenly body and the aggregation constant at radius RH, ka,R = 2.244171 × 1025 such that,
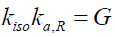 (43)
(43)
That is, G is the well-known gravitational constant G = 6.67384 × 10-11 m3kg-1s-2.
Therefore, from (20), (22) and (40), the photon deflection αH caused by a heavenly body H is given by,
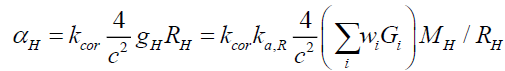 (44)
(44)
For similar size, mass but different ages as nucleosynthesis produces different hydrogen-helium ratios, different Gi should produce different photon deflections αH. That is, the distant the galaxy and therefore, younger the greater the bending of light, than closer, older galaxies. This is, therefore a test for the variability of the gravitational constant.
Revisiting Schrodinger
This paper is the latest paper in the 18-year search for “new” physics. The objective of this research evolved from just determining if gravity modification was theoretically and technologically feasible [3,6,15-19] to documenting [3,4,5] paradoxical axioms in contemporary physics and how changes in these axioms produce different, simpler models in physics [5,18], to rewriting physical phenomena [7-10,15,18].
There are three prerequisites that drive this analysis and theoretical model development. First, any new theoretical model should be vindicated by the empirical data. Second, per Occam’s Razor, these theoretical models should be simpler than those in contemporary physics. And third, that these theoretical models provide easily testable new experiments. All three have been achieved to date.
Solomon [6,7,15,17] proposed that it was the spherical shape of the electron’s charge that causes the force experienced by a moving electron to be orthogonal to the magnetic field lines and its velocity. This explains why this force is derived from the cross product in contemporary electromagnetic theory. Therefore, deconstructing particle structure [5-10] is a necessary requirement to explaining particle behavior.
Taking this a step further, Solomon [5] and Solomon and Beckwith [7-9] proposed additional particle structure deconstruction. That photons are umbrella shaped, a flat “umbrella” disc consisting of the probability disc with oscillating electric and magnetic vectors buried in this disc and the “umbrella handle” of the motion or velocity vector which is orthogonal to the disc. Solomon proposed [5,8] that this oscillation is derived from the rotation of the electromagnetic vectors between spacetime and subspace, thereby guaranteeing conservation of energy within the transverse wave.
This umbrella model of the photon, explains why “orbiting” electrons in the electron shell do not exhibit synchrotron radiation as their motion vectors are aligned with the direction of the electrostatic attraction of the nucleus.
Quantum theory [19] assumes that a particle can be anywhere in 3-dimensional space and is presented as the spherical symmetry of it potential as a function only of its distance from the center origin. However, given that a particle has a velocity, a particle can only appear in the space in front of it, not behind. When photons or mass particles pass through a pinhole and they show up on an opaque screen as a Point Spread Function PSF. Placing the opaque screen behind the photon path will not produce this PSF. Therefore, in motion, this spherical symmetry is broken.
In quantum mechanics momentum is represented by the momentum operator,
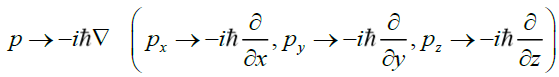 (45)
(45)
However, if spherical symmetry is required, (assuming photon travel along the z-axis) forward motion eliminates the zcomponent of this momentum operator, as no backward potential exists, leaving only the x- and y-components of this momentum operator. If spherical symmetry is not required than only the positive z-component exists, but raises the question, why would potential be hemispherical?
The logical inference is that the z-component is eliminated altogether. This leaves a disc shaped momentum operator. However, this disc structure is orthogonal to the motion vector. The inference is that this disc is the carrier of mass and energy of the particle. Or the particle is umbrella shaped when combined with the motion vector and this disc-shaped momentum operator can be written as,
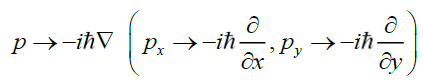 (46)
(46)
Since, in flat spacetime, the disc is symmetrical, converting into radial coordinates (r, θ), for a radial distance rp from the center of the disc or motion vector gives,
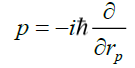 (47)
(47)
Note, using the photon, the probability and energy field disc are orthogonally positioned with respect to the motion vector of velocity c. The transverse electromagnetic wave travels along the motion vector. Thus, electromagnetic fields oscillate about the motion vector. However, the PSF is the projection [5,7,8,9] of the photon’s 2-dimensional disc. These are two different phenomena that have a “common denominator”, the wavelength.
Unlike, quantum theory’s energy operator for a kinetic energy Eke is given by,
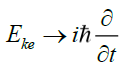 (48)
(48)
this energy of the photon is not a function of time, but in a gravitational field it is a function of the spatial gradient [5,6] of the gravitational field. Therefore, for photons, the energy operator is eliminated and there is no necessity to introduce potential.
Without a clear understanding of mass as an intrinsic function of particle structure, as opposed to Higgs Field which is extrinsic to particle structure, it is not possible to determine the effect of potential on mass particles. Solomon [5,7,8] introduced the concept that mass consists of bound photons. If that is the case then potential is no longer a consideration for all particles, mass or massless.
Addressing infinities
Returning to the Probabilistic Wave Function [5-9] (49) – (54), that generates the Point Spread Function, one can infer some properties of Nature.
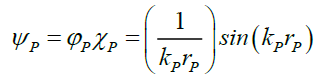 (49)
(49)
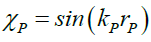 (50)
(50)
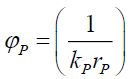 (51)
(51)
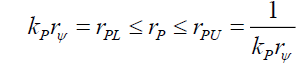 (52)
(52)
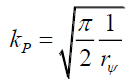 (53)
(53)
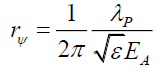 (54)
(54)
Nature shows that (49) is smooth, continuous function that does not go to infinity, therefore, the lower limit rPL of the radius of the photon’s probabilities disc radius rP should decrease to zero, or
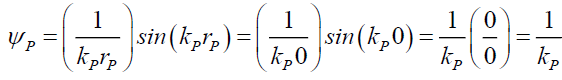 (55)
(55)
Nature shows that, provided numerator decreases to zero faster than the denominator, which is the case here, a function y (56) like (49) with coefficients a and b,
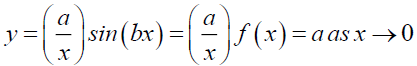 (56)
(56)
reaches a constant term, provided
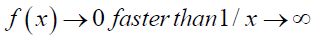 (57)
(57)
Or in general one can propose that a function f(z) having infinities is a constant, if both the numerator function fn of x and denominator fd of y approach zero provided the numerator function approaches zero faster than the denominator function,
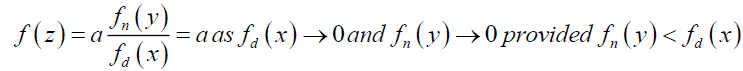 (58)
(58)
This therefore is a method to solving some of the infinities problems in quantum theory.
Conclusion
With respect to photon probability, this paper shows that though photon probabilities are altered by the gravitational field, the bending of light by α degree is independent of the photon energy or frequency and therefore the strength of its probability field. The shift in the CP0 is what causes the shift in the motion vector. It is now possible to further deconstruct particle structural properties. With respect to motion, the gravitational motion effect occurs on the umbrella handle or the motion vector, not the umbrella disc and therefore, (33).
An additional note: Assuming that the laws of physics are consistent anywhere and everywhere in the Universe, even at the nano- or pico-scale, Special Theory of Relativity (5) requires that at a velocity less than that of light c, length in the direction of motion elongates with less velocity and thus the photon’s electric and magnetic field vectors will thicken if the velocity of the photon is slowed in flat empty spacetime. However, by (5) at this juncture it is not possible to determine what the “rest’ thickness of these field vectors would be and more research is required.
References
- Efstathiou G, Pryke C, Steinhardt P, et al. Spotlight live: Looking back in time-oldest light in existence offers insight into the universe. The Kavli Foundation;2015.
- Nemiroff R. Bounds on spectral dispersion from Fermi-detected gamma-ray bursts. Phys Rev Lett. 2012;108:231103.
- Solomon BT. New evidence, conditions, instruments and experiments for gravitational theories. J Mod Phys. 2013;8A.
- Solomon BT. Non-gaussian photon probability distributions. In: The proceedings of the space, propulsion and energy sciences international forum (SPESIF-10). Glen AR, editors. AIP Conference Proceedings 1208; Melville, New York; 2010.
- Solomon BT. Super physics for super technologies: Replacing Bohr, Heisenberg, Schrödinger and Einstein, Propulsion Physics Inc, Denver March; 2015.
- Solomon BT. Gravitational acceleration without mass and non-inertia fields. Phys Essays. 2011;24:327.
- Solomon BT, Beckwith AW. Probability, randomness and subspace, with experiments. J Space Explor. 2016;6(1).
- Solomon BT, Beckwith AW. Photon probability control with experiments. J Space Explor. 2016;6(1).
- Solomon BT, Beckwith AW. Probability as a field theory. J Space Explor. 2016;6(1).
- Solomon BT, Beckwith AW. The origins of gravitational fields. J Space Explor. 2016;6(1).
- Wahlin L. The Bending of Light by Gravity. www.colutron.com/download_files/Bend.pdf.
- http://home.fnal.gov/~syphers/Education/Notes/lightbend.pdf.
- Goobar A, Amanullah R, Kulkarni SR, et al. iPTF16geu: A multiply imaged, gravitationally lensed type Ia supernova. Science. 2017;356(6335):291-95.
- Amoros RL, Hunter G, Kafatos M, et al. Gravitation and cosmology: From the Hubble radius to the Plank scale. Proceedings of a Symposium in Honour of the 80th Birthday of Jean-Pierre Vigier. Kluwer Academic Publishers, Boston, MA; 2002.
- Solomon BT. An approach to gravity modification as a propulsion technology. In: The Proceedings of the Space, Propulsion and Energy Sciences International Forum (SPESIF-09). Glen AR, editors. AIP Conference Proceedings 1103; Melville, New York; 2009.
- Solomon BT. Reverse engineering Podkletnov’s experiments. In: The Proceedings of the Space, Propulsion and Energy Sciences International Forum (SPESIF-11). Glen AR, editors. Physics Procedia, Elsevier Science; 2011.
- Solomon BT. An introduction to gravity modification: A guide to using Laithwaite's and Podkletnov's experiments and the physics of forces for empirical results. 2nd edition. Universal Publishers, Boca Raton: 2012.
- Solomon BT. Empirical evidence suggests a need for a different gravitational theory. American Physical Society (APS) April Conference, Denver; 2013.
- Griffith D. Introduction to Elementary Particle. 1st edition, Wiley-VCH; 2004.

