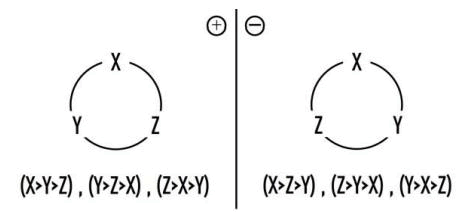Research

, Volume: 13( 1) DOI: 10.37532/2320-6756.2025.13(1).353

• View PDF
• Download PDF

On the Physics of Spontaneous Symmetry Breaking in a Binary Field

*Correspondence:

En Okadal
Department of Physics, Nagoya Bunri University, Aichi, Japan
E-mail: enokada0324@gmail.com

Abstract

We propose a novel theoretical paradigm in which all physical realities can be concretely defined by the degree of symmetry breaking in a binary field, providing an alternative interpretation of the Higgs mechanism with vivid physical images. Together with a newly proposed hypothesis that the Planck constant evolves with the cosmic scale factor, which drives an evolution of the mass and electric charge of elementary particles, our model could solve a bunch of hierarchy problems in theoretical physics at one shot, demystifying all the four fundamental interactions as different aspects of a singular consistent story.

Keywords

Beyond standard model; Super unified theory

Introduction

We would like to dedicate our paper to Dr. John Wheeler, the man who conceived the slogans of “It from bit” and “Law without law”. He was undoubtedly the closest figure who could have reached exactly the same conclusions 40 years ahead of us. It is no exaggeration to say that our paper is all the way reaffirming the greatness of his insights that sharply hit the deepest truths of our mother nature [1].

Wheeler was right to realize that all kinds of existence can only be defined in contrast to non-existence, therefore all physical realities can be reduced down to a collection of binary choices between 0 and 1 of supreme and ultimate abstraction. However, it is not the bit information carried in the collection, but the degree of asymmetry of a digital field that gives rise to all physical realities.

Suppose a field comprised of discrete “atoms” or “cells” that can take value of either +1 or −1 (namely two opposite states) with equal probability (1/2 each) and that adjacent atoms would instantly “annihilate” to erase both of their values to zero. The well-established theory of Bernoulli trial tells us that we can expect a surplus favoring one sign to the other, which cannot find partners for annihilation, by a magnitude proportional to the square root of the number of atoms. Let us arbitrarily denote the surplus as 1, hereafter [2].

Literature Review

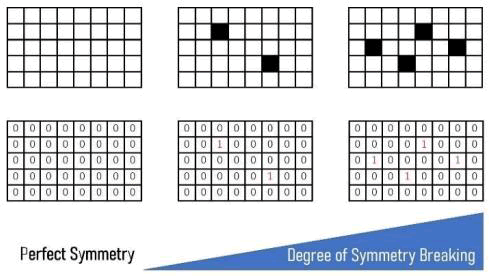
A field with perfect symmetry, namely all of its constituent quanta take value 0 instead of 1, has nothing existent in it. Physicists do not have to worry about such a deadly quiet world with no subjects of and thus no need for physics at all (Figure 1).

FIG. 1. Degree of symmetry breaking.

The field shall certainly have an average probability density for the occurrence of the “flip” from 0 to 1 (it is essentially equivalent to regard the stochastic surplus as probabilistic flipping from ground state to excitation state, which is more convenient for our discussions hereafter), namely per how many quanta on average can we find a 1, out of numerous enough quanta such that the law of large number works. With such an average, we can now quantitatively define the degree of symmetry breaking in specific areas of the field, using the exponential distribution. Note that no matter how complicated a configuration might be and regardless of its number of dimensions, it can be ultimately broken down to a collection of bilateral pairs of 1 (“pair” hereafter) [3].

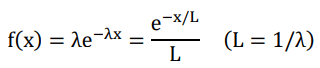
The mathematical feature of exponential distributions tells us that the distance (“length” hereafter) between the pair of quanta (measured by multiples of a unit length as will be calculated shortly) has an expectation of

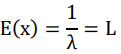
and an upside accumulative probability of

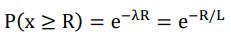
We can exploit this feature to quantify the “rareness” of a specific pair out of the total population, as the asymmetry it adds to the field. By taking the negative of natural logarithm of the upside accumulative probability, we obtain a linear function of R, the larger the rarer.

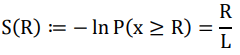
The extreme abstractness of the flipped quanta means that all of them equally take the state 1 (there are no values such as 1.5 or 2 or π). Therefore, length is the only variable that can distinguish the pairs since every pair has two flipped quanta alike. With a barometer proportional to the length, now it is quite natural to define another barometer that is inversely proportional to the length. Let us assign coefficients to them as below, somehow all of sudden but of course they did not come out of nowhere [4].

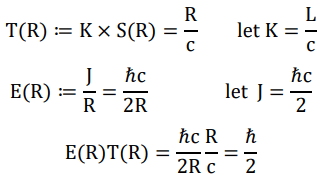
As we shall see the evidence that support our hypothesis, E(R) and T(R) are exactly the concrete definition of time and energy respectively. We have been using the notions of time and energy totally intuitively, without noticing the profound meanings behind them.

Furthermore, it is exactly the probability density of the flip of spatial quanta that quantum mechanical wave functions describe.

The reason why the amplitude square of the wave function gives the probability density to find out a Fermion is rightly because Fermions are defined by two flipped quanta, square means two flips simultaneously occur in the vicinity of the locus. After all, we cannot define the degree of asymmetry with a singular spatial quantum, pair is both the minimal and the most reasonable unit to focus on [5].

Given that the energy of a pair is defined proportional to the inverse of its length, the force acting between the quanta, from its definition as the derivative of energy by distance, must be proportional to the inverse square of the length, regardless of the number of spatial dimensions. It is this very nature of the force being generally proportional to the inverse square of distance that dictates only 3-dimensional field canstably andself-consistently exist, insteadof the logic of the contrary ash as long been wrongly believed.

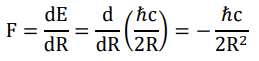
The sign of the force between quanta shows it is universally attractive. As the final result of such an attraction, we may naturally expect a situation in which two quanta areback-toback, forming a “binary star system” with a diameter twice the expanse of a spatial quantum.

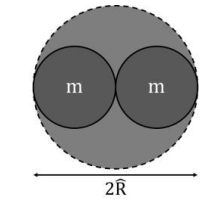
The diameter of spatial quanta (2R), which serves as the minimal length unit in our binary field, can be reasonably calculated supposing when two spatial quanta are brought within a spherical region of diameter R, they will instantly form a mini-black hole according to our definition of energy. (The illustrated situation in below does not really occur, which is only hypothetical in order to calculate R) (Figure 2) [6].

FIG. 2. The diameter of spatial quanta.

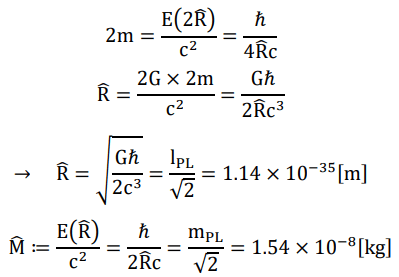
From now on, 2R(√2lPL) will serve as the yardstick in our binary field, together with a series of quantized mass on lanck scale, corresponding to quantized states which can only have diameters in multiples of 2R.

Discussion

Particle physics

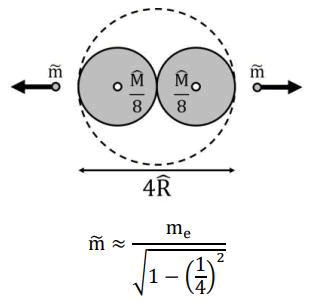
Let us begin to exhibit the evidence that support our hypothesis. Firstly, the calculation in below suggests that electron-positron pair production might be a breaking of equilibrium where the gravitational attraction holding two mass lumps was beaten by counteracting electromagnetic forces applied on two tiny portions of them (Figure 3) [7].

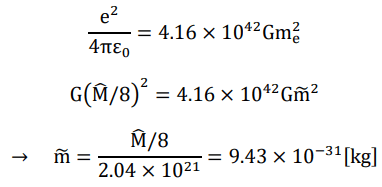
FIG. 3. Particle physics.

At first glance, there could be several equally probable or essentially indistinguishable interpretations about what is actually happening behind the calculation. However, after rounds of scrutiny, we assume the below story is the best match to our hypothesis and thus most likely to be the case.

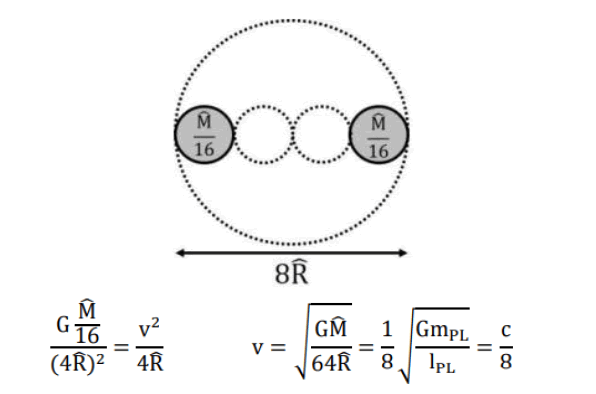
A pair of back-to-back spatial quanta (diameter 4R) with a combined mass of M/4 (thus M/8 per spatial quantum) is rotating at velocity c/4, in which the two quanta as seeds of electric charges rotate in opposite mode. The Lorentz factor of c/4 may rightly come from the hypothetical rotating velocity (they may not physically rotate in such a closest vicinity) of two lumps of mass M/8 that are separated by 2R, according to ewtonian calculation. (Note that the is not the distance between the centers of the two lumps, but instead the distance from the barycenter of the binary stars to the surface of the dotted outer sphere. serves as the marginal spatial expanse (>0) of mass points, therefore further specifying point loci within 2R is nonsense) [8].

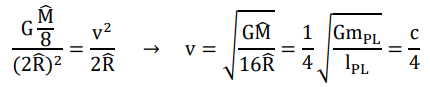
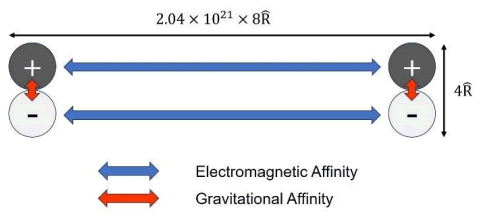
Each seed at this stage only carries an imaginary charge of +e/2 or −e/2 and does not exert electromagnetic forces (either attraction or repulsion) until it finds a partner of the same character through a kind of “electromagnetic affinity” to form a real charge. If there exists another pair within a distance of 2.04 × 1021 × 8R, the electromagnetic affinities acting in between (instead of 4R is because the strength has to be doubled) shall overcome the “gravitational affinity” that holds each of them within its sphere of diameter 4R (Figure 4).

FIG. 4. The figure shows electromagnetic affinity and gravitation affinity.

The two pairs will then exchange partners, forming two new pairs, now with synchronized rotation mode, namely the origin of elementary charges. Their mass is now

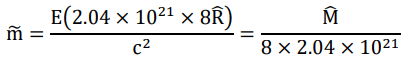
in accordance with the initial length of the two new pairs. Note that even though they will in turn shorten the distance between the spatial quanta, their mass shall be fixed at m , with both the shrinkage of distance and the increase of angular momentum rather contribute to the formation of an authentic electric charge. The reason why the detectable rest mass of electron me needs a “backward” Lorentz adjustment from m will be revealed later with persuasive explanations.

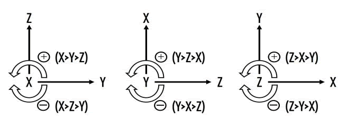
Among the three spatial dimensions, suppose they are not completely homogeneous in nature, then there will be two intrinsically different permutations as shown in below. This very fact provides us with a unique way to define two different modes of rotations whose axis can be arbitrarily tilted in the three-dimensional space. (The permutation can be uniquely defined by the descending order of the values of X, Y, Z coordinates of the unit vector pointing the north pole of the axis, in whose eyes the rotation looks anti-clockwise, for example) (Figure 5) [9].

FIG. 5. There will be two intrinsically different permutations as shown in below.

As we shall see later, the magnitude gap between gravity and electromagnetism is nothing but a reflection of the fact that the current probability density of quanta flip is exactly 1/(2.04 × 10²¹), the inverse square root of 4.16 × 10⁴². Moreover, as will be further studied in the cosmology part, this figure evolves with the cosmic scale factor or the age of the universe, which in turn provides astoundingly beautiful and simple solutions to all of the hierarchy problems. (Note that the hierarchy gap we used here is actually the extreme case, namely in the electron-electron interactions, instead of electron-proton or proton-proton interactions.

Similar calculations do hold in the latter two cases, however, as we shall see shortly, it is the hierarchy gap in electron electron interactions that holds the key to unveil the secret behind gravity and electromagnetism. Just as we will never find the astounding and precise relationship between the Planck scaled physical quantities and those of elementary particles, as far as we only pay attention to the Planck length and mass without the critical divisor √2 in R and M.

As mentioned earlier, those flipped spatial quanta can be regarded as unannihilated surplus after a series of Bernoulli trials choosing one of two opposite states with 50%:50% probability. On the surface of cosmological event horizon, it should have a total number of flipped quanta proportional to the square of its radius, thus the expected surplus should be proportional to its radius. An easy integral along the radius gives us a total number of flipped quanta proportional to the square of the cosmic radius, thus the average probability density of quanta flip shall be inversely proportional to the radius (square divided by cube). Note that since the increase of the number of spatial quanta within our cosmological event horizon is a step-by-step process in accordance with the growth of cosmic age, we cannot brutally conclude that the probability density shall be inversely proportional to the square root of the Hubble’s volume, by simply regarding the volume as a measure of the total number of Bernoulli trials.

We may take another approach as well. Suppose there is a primordial wave function that governs the probability destiny of the entire universe, propagating at the speed of light, all the way from the singularity (we now should say a spatial quantum, instead of a point with no volume) and literally pioneers the frontier of the universe. Whichever explanation may you prefer, either by the conservation of energy or the mathematical property of three-dimensional Laplacian, the amplitude of that wave shall be inversely proportional to the distance from its origin. If we take the extension of the frontier of the wave as the expansion of space, we may find that the effect of space expansion to dampen the amplitude of waves rightly makes ends meet such that the probability density settles to exactly the same magnitude everywhere in the universe. This wave can be regarded as the Master or Mighty or Mother wave for all subsequent wave functions of specific particles. We shall revisit the essence of such a wave, when the time is ripe.

Let us present some interesting calculations which support our hypothesis, with less clarity for exact interpretations at this stage, thus remain to be further elucidated.

Mean lifetime of free neutron

Taking the figure τ beam ≈ 880 [s] measured by the so-called beam method, it shall hardly be a coincidence that

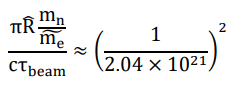
where m_n is the rest mass of neutron, m e is the relativistic electron mass adjusted by the Lorentz factor of c/4. This calculation implies that β-decay (and maybe the weak interaction in general) might be a phenomenon which is rightly characterized by the stochasticity of the spontaneous symmetry breaking in the binary field.

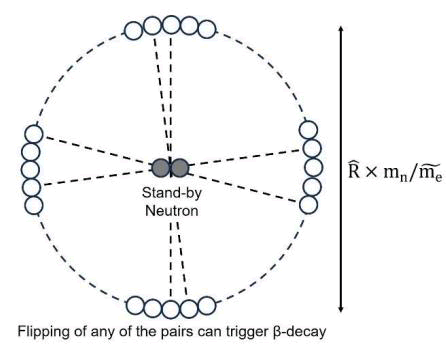
As a probable explanation for the meaning of the coefficient π and mn m e, we could reasonably guess that the release of an anti-neutrino in β-decays (which is equivalent to an absorption of a neutrino) may actually be a participation of two additional flipped quanta that are needed for the fission of a stand-by neutron (two quanta) into a proton and an electron (four quanta in total). The requirement for the two additional flipped quanta is they must occur at the opposite loci on the equator of a sphere with a radius of 1840R, reflecting the fact that the “electromagnetic affinity” to form a proton-type electric charge is less powerful than that of the electron-type (the origin of the difference will be explained in detail shortly). πmn m e means the freedom in choosing which diameter the two flipped quanta to reside, while (2.04 × 10²¹)⁻² is simply the probability to observe two flipped quanta on the two ends of a specific diameter (Figure 6).

FIG. 6. Flipping of any of the pairs can trigger ?-decay.

Moreover, there is a well-known conundrum that the mean lifetime of free neutrons measured by the so-called bottle method is τ_nbottle ≈ 88 [s], which is inexplicable within the range of experimental error. We noticed that this gap can be well enough approximated by the Lorentz factor of c/8,

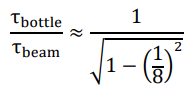
a velocity we may obtain supposing two quanta are rotating with a diameter of 8R instead of 4R (Figure 7).

FIG.7.A diameter of 8R instead of 4R.

It may have something to do with the participation of the two additional quanta, which cannot get closer than due to the existing stand-by free neutron. The case may be that in the bottle method, our focus is those undecayed stand-by neutrons without the additional quanta, while in the beam method, we focus on the decayed neutrons thus with the disturbance from the additional quanta with velocity c/8, which may in turn result in an extra mass of the system and prolong the lifetime. In short, the mysterious discrepancy may be caused by the fact that we were actually observing two slightly but intrinsically different phenomena.

Mean lifetime of the Higgs Boson

As the latest figure, τ_Higgs .1(+ .3 −0.9) × 10⁻²² [s] agrees well enough with the calculation in below that has a clear similarity with the case of free neutron.

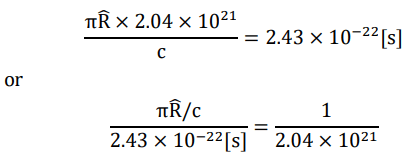
This calculation strongly suggests that the Higgs mechanism could be exactly a rephrase of the spontaneous symmetry breaking of our binary field.

Next, let us move on to the implications of our hypothesis on the strong force. In particular, we will first mathematically calculate the mass of up quark and down quark, and then reveal the physics behind the color charges, together with the true mechanism of the asymptotic freedom and the so-called quark confinement.

As mentioned earlier, the calculation that has implied the possible mechanism of electron-positron pair production applies to proton-antiproton pair production as well, by adopting the hierarchy gap of proton-proton interactions. The fact implies a mass-independent general relationship, which can be put into the equation in below.

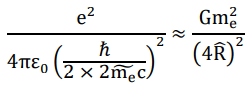
It means that the electromagnetic repulsion between two unit-charges sit at a distance correspondent to the energy required for a pair production of two Lorentz adjusted masses (by the factor of c/4) structurally balances with the gravitational attraction between the rest masses sit at a distance of 4R. It nicely matches with our proposal for the underlying mechanism behind the origin of electron mass.

This mass-independent relationship can be simplified to a more familiar form, which may have strikingly reveled the secret behind the fine structure constant α.

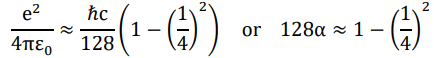
13.036 might be 128 adjusted with the square of Lorentz factor of c/4, plus some higher order refinements.

Another implication from the equation is somehow latent or stealth, but its profound impact may be far beyond our first impression. The equation shows that

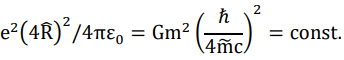
You may want to ask, aren’t the figures on the left-most side all constants? Let us explore the possibility that if they are not Electrons and protons have different mass-charge ratios, but how sure are we about the identity or uniformity of electric charges? In other words, what if the real case is that the mass carried by proton, by some unknown mechanisms, has a lesser reactivity to electromagnetism such that proton needs more mass than electrons to take part in electromagnetic interactions equally?

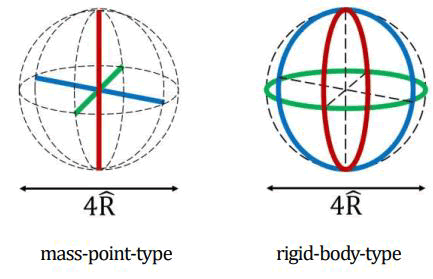
As for how the part of 4R might be variable, the first idea that came up to our mind was that the mechanics of rigid bodies are much richer than that of mass points. What if proton and neutron are a kind of rigid-body-type particles whereas electron is a mass-point-type particle?

Note that we have already excluded the concept of zero distance in our binary field, thus even for mass points, they still have a minimal diameter of 4R? (as they consist of two quanta). “ oint” just means it does not have any rotational degree of freedom. Moreover, we may reasonably postulate that the length of spatial “span” of a rigid-body-type degree of freedom is π times that of a mass-point-type one, as the latter is kind of restricted within the diameter of the former (Figure 8).

FIG. 8. Mass point type and rigid body type.

Next, let us suppose that in the high energy hadron collision experiments, the smashed nucleons may instantly reduce one or two of its three rigid-body-type degrees of freedom down to the mass-point-type. If we define an “effective span” of degrees of freedom by taking the geometric average of the span on all the three dimensions, we shall obtain the below figures expressed with fractional powers of pi, indicating how “bulgy” the partially shrunk rigid-body-type particles still are, compared with the genuine mass-point type one (Figure 9).

FIG. 9. One dimension shrank and two dimension shrank.

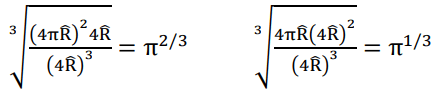
The inversely proportional relation of charge and span shown in our equation implies that a larger effective span shall diminish a mass’s responsiveness to electromagnetism. Therefore, each partially shrunk state of the mass lump shall have an inferior electromagnetic responsiveness by factors of respectively, compared with the mass-point-type electron.

Suppose the two spatial quanta evenly contribute to the electromagnetic responsiveness of the Fermion that they collectively define, then each spatial quantum would have an electromagnetic responsiveness further inferior to that of electron, by factors of 1/9.2 and 1/4.3 respectively. A lesser electromagnetic responsiveness means a larger mass required to behave as an electric charge, therefore, the theoretical mass of a singular spatial quantum in the partially shrunk rigid-body-type particles shall be 9.2 and 4.3 times of the mass of electron, respectively. They are exactly the theoretical mass of down quark and up quark.

With the convincing calculation of the mass of up quark and down quark, our hypothesis of the concept “electromagnetic responsiveness” shall have gained sufficient credibility. Now the time is ripe to reveal the reason why the mass of electron and positron is not twice of our illustrated fission product. In short, electric charges are obtained in exchange with mass. Each half of the rotating mass lump did nolongerhavea mass of and a unit charge, but was actually giving up half of its mass (reserving the other half as its mass) to acquire 1/2 of a unit charge. It was in this way that the combined particles had exactly the mass of electron and a unit charge. In other words, electromagnetic responsiveness shall be regarded as a conversion factor between mass and electric charge, or the efficiency of a specific type (mass point or rigid body) of mass to acquire and maintain a unit charge.

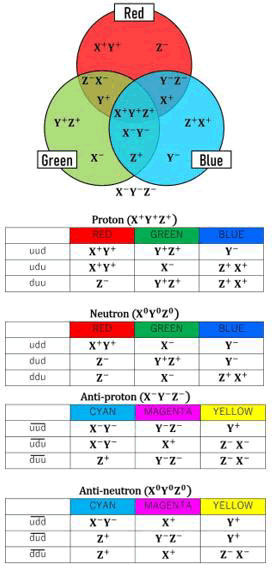
Our discussions so far strongly suggest that the entity of quark is rather one of the two spatial quanta within a partially shrunk rigid-body-type particle, namely hadron, in high energy collisions. It only transiently interacts with one of the two spatial quanta that collectively define the incoming leptons, and let them scatter. The form of quark, as a singular quantum in a transiently shrank hadron, can only exist together with its partner quantum, therefore, it does not make sense outside of hadrons. Detectable Fermions are, after all, defined by a pair of quanta, thus the visionary state of “quark” does not independently exist. This shall be the secret of the so-called quark confinement. The color charge of quark may highly likely to be a reflection of the details of the shrunk dimension(s) as shown in the schematic figure and tables in below, just for an example (Figure 10).

FIG. 10. The color charge of quark may highly likely to be a reflection of the details of the shrunk dimension(s) as shown in the schematic figure.

If one dimension has shrunk, the transient state would have an imaginary electric charge of ± 1/3, reflecting the fact that one out of three dimensions is mass-point-type (same with electrons). If two dimensions have shrunk, the charge would be ± 2/3 by similar logic. Down quark (one dimension shrunk) has a larger geometric mean of spatial span than that of up quark (two dimensions shrunk). It may well explain why nucleons have their respective charge radii and mass radii, as the superposition of mass and the offset of electric charges take place respectively, in an independent manner deservedly as our model predicts.

The sign of the fractional charge of quarks may reflect the mode of rotation of the shrunk particle seen from each dimension. By the aforementioned definition of the rotation mode, we can define not only the mode of the entire particle, but also the mode seen from each axis of spatial dimension. The illustration in below is for an example (Figure 11).

FIG. 11. The illustration example.

Now that it is almost needless to say that the information about the rotation modes is conveyed by the wave function of particles for sure. And more importantly, this rotation of spatial quanta beneath the detectable particle they actually define, is exactly there a son why quantum mechanical waves must be defined as complex functions. The necessity to use complex numbers in describing the dynamics of the spatial quanta might be due to the historical inevitability that we had chosen (of course not by accident) real numbers to construct the physics of the detectable particles with which we are much more familiar. Furthermore, the properties of complex number, or imaginary number in particular, turns out to be the final sentence to the theory of QCD, as we have found a strikingly simple solution for how could protons be held harmonically together within atomic nuclei.

Before moving on to the highlight of this paper, let us add some complemental comments about the mass of proton. Proton has a mass about 1836 times that of electron. It is a well-known fact that 6π5 is a good approximation of 1836.

Out of the 6π⁵, proton as a genuine rigid-body-type particle shall be an inferior reactor to the electromagnetic force than electron by a factor of 1 π² (as all three dimensions are rigid-body-type). The remaining 1 6π³ might be a factor reflecting a qualitative leap from mass-point-type to rigid body-type. In other words, the logic of our calculation of theoretical mass of u quark and d quark compared with electron may only apply for particles that have at least one mass-point-type dimension. Although its mechanism needs to be further elucidated, the assumption does not sound so unreasonable either, as 6 is the degree of freedom of a three dimensional rigid body, while π³ could be the ratio of “effective volume” (the product of spans over all the three dimensions) between rigid-body-type and mass-point-type particles. It is interesting to note that the theoretical mass of strange quark is about 186 times of the electron mass, and 1 6 is a good enough approximation of 6π³.

Next, let us unveil the secret of the nuclear force that holds protons and neutrons together. Suppose a homogeneous sphere with a uniformly positive charge density, as a good approximation of atomic nucleus. The below equation of radial motion, with a fairly simple integration, gives us an equation about the velocity. Let the constant of integration be zero, which is equivalent to the conserved mechanical energy is zero, as the most simplified situation for our thought experiment.

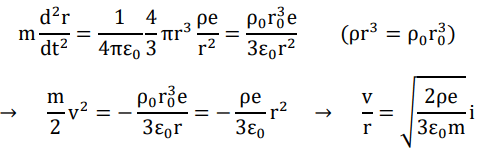
The equation looks nonsense in the conventional context, since the square of the velocity is negative. However, being free from all kinds of prejudice, if imaginary velocities are allowed, what will happen? A direct consequence shall be that the Lorentz factor turns out to be smaller than one. Having paved the way for quite a while, we believe that now an idea that this imaginary number velocity represents the motion of the spatial quanta may not sound abrupt, which is highly likely to be the case.

Substitute the actual figures of the unit charge, the mass of nucleon, the permittivity of vacuum, the charge density of proton as the average charge density of atomic nuclei, into the equation. Then multiply the resulted “Hubble constant” in atomic nucleus with ~10⁻¹⁵[m] as the order of its radius. Surprisingly, we may notice that the imaginary velocity falls to exactly the same order with the speed of light. At such a velocity, the aforementioned smaller-than-one Lorentz factor would rightly result in a relativistic mass lighter than rest mass by a few percentage points, which matches well enough with the binding energy per nucleon for the elements of double-digit atomic number.

Our approximation may not work well enough for the atomic nuclei of light elements since their charge density shall be far from homogeneous. Note that the imaginary velocities are theoretically proportional to the distance of the nucleons from the center of atomic nucleus, thus the magnitude of the relativistic mass reduction (or the level of binding energy) increases with the growth of radius. This is exactly the underlying mechanism of the so-called nuclear force that shares similarities with the asymptotic freedom of quarks, a concept that was earlier demonstrated to be unnecessary in explaining the quark confinement and therefore could now be completely abandoned.

As for the motion of the spatial quanta within atomic nuclei, the most reasonable explanation should be that they switch their “owners” just like the free electrons in metals. It is by such a sharing of spatial quanta that nucleons can reach a less massive and thus more stable state.

Due to limitation of space, we will not go any further into detailed quantitative discussions on specific atomic nucleus. However, it may not diminish the persuasiveness of our hypothesis by a little bit, we firmly believe.

The discovery of imaginary velocities urges us to slightly correct our previous equations. Instead of multiplying the Lorentz factor of c/4 or c/8, we should divide that of ci/4 or ci/8, which do not make too much difference except we may obtain a closer approximation of the fine structure constant. We have intentionally ignored the slight difference, since the time would only be ripe at this stage to reveal the secret in behind. In short, the rest mass of elementary particles needs a “backward” adjustment from pure theoretical calculation rightly because the rest mass in our perspectives is the relativistic mass from the view point of spatial quanta, and the former is always lighter than the latter because of the imaginary velocity.

Our discussions have almost reveled all the major secrets of the strong force. However, without explaining the origins of so many exotic baryons and mesons, our hypothesis might not acquire full credit for sure. So, now let us cope with it. Adopting the Lorentz factor adjusted proton mass as one unit of the standard nucleon mass in collision experiments,

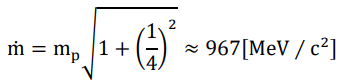
we may find with great surprise that the mass of the 16 baryons (other than proton and neutron) that supposedly to consist of only u, d or s quarks align in an extremely elegant pattern.

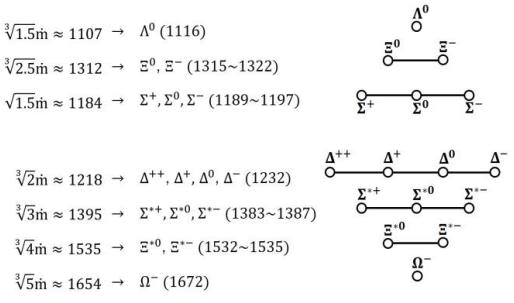
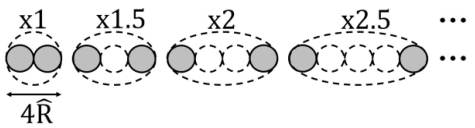
It strongly suggests that exotic baryons are actually transient figures of nucleons during high energy collision, expanding one of its three spatial dimensions in a discrete manner (Figure 12).

FIG. 12. Expanding one of its three spatial dimensions in a discrete manner.

In contrast to the deep inelastic scattering in which we can just indirectly assume that nucleons have inner structures from the scattering pattern of electrons, hadron collision experiments do actually churn out numerous detectable baryons and mesons. The difference is that, exotic hadrons, though very short-lived, are nonetheless made of spatial quanta pair, and are genuine rigid-body-type particles as carriers of electric charge. Compared with proton, the electromagnetic responsiveness of each excitation state should be, by the same logic with the calculation of quark mass, inversely proportional to their effective span, to explain their increased mass. The effective span shall be reasonably calculated by equally distributing the span of the expanded dimension onto all three dimensions, therefore the cubic roots of half-integers or integers. (The reason why square root of 1.5 gives rise to sigma baryons remains to be studied. The case might be one of the three dimensions had collapsed first, then the two-dimensional “disk” expands one of the remaining two). The reason why the cubic roots of integers correspond to spin 3/2 baryons while the cubic roots of half integers give rise to spin 1 baryons may due to the fact that the former are expansions in multiples of 4 , which may render the baryons an additional integral spin by a mechanism that awaits further study.

In summary, quark is one of the two quanta that define a partially shrunk nucleon in which one or two of its three spatial dimensions transiently collapse from rigid-body-type to mass-point-type degree of freedom. Gluon is the spatial quantum exchanged in the transitions between the different states of shrinkage. Exotic baryons are nucleons transiently expanded along one of its three dimensions, while mesons are the energy exchanged during the transition between these different states of expansion. The dazzling varieties of the cascades in hadron decay are probably the reflections of the probable transitions among all possible states, which shall be explained with no big problem in the context of our model, as a matter of time.

Moreover, it is interesting to note that the mass of baryons with c quark substitution and b quark substitution are generally and roughly twice and five times heavier than their counterparts made of only u/d/s quarks, respectively. It implies that nucleons may have three intrinsically distinctive modes for the transient expansion of its spatial dimensions, namely which one of the three dimensions to be expanded. One natural explanation could be that compared with the first and the easiest choice that gives rise to those baryons supposed to be made of u/d/s quarks, the second and third harder choices may, for some unknown reason, result in a much weaker electromagnetic responsiveness by a factor of ~1/8 and ~1/125 respectively, which in turn generate baryons roughly twice and five times massive than those generated by the first mode. It may not be meaningless to point out that the ratio between the mass of tau on and muon is roughly 136:8, though we have no idea where comes the residual ~8π (after dividing the mass of muon by 8me).

The heterogeneity among three spatial dimensions is likely to be the reason why the P-symmetry is broken in the weak interaction. If the three dimensions are homogeneous, we may no longer be able to distinguish the two intrinsically different modes of rotation as we have proposed earlier. From this point of view, it is rather natural that right-handed spin and left-handed spin should differ to each other in an inherently distinguishable fashion. Note that the weak force is the only interaction where the numbers of participating spatial quanta do not conserve before and after the process. In other words, it could rather be a phenomenon becoming noticeable to us rightly because of the addition of newly flipped spatial quanta to the pre-existing physical system we had been observing. The reason why only the Bosons for the weak interaction possess mass, may be the very reflection of this non-conservation of the number of flipped quanta before and after the process.

After all, electric charge is a vectorial property generated out of the rotation of spatial quanta as a culmination of the universal attraction between them. The strong force can be bisected into two parts. The binding of nucleons within atomic nuclei can be explained by their sharing of spatial quanta just like the free electrons in metals, where the motion of spatial quanta with imaginary velocities contributes to a relativistic mass reduction, stabilizing the atomic nucleus in the form of binding energy.

Those phenomena that imply any inner structures of hadrons are indeed the transient snapshots of them, which should not have been even noticed unless they were smashed to each other in the ultra-high energy colliders.

The mathematical structure of QCD exactly reflects the fact that the three rigid-body-type dimensions of nucleons may randomly change their type or extend their spatial span under high energy conditions. The weak interaction shall be rather regarded as an inevitable consequence of the spontaneous symmetry breaking of the binary field, which occurs whenever two additional flipped spatial quanta are brought by the universal attraction to the vicinity of an existing particle.

Our theory vividly explains, with clear cut physical images, why electromagnetism, weak force and strong force are respectively linked with U (1), SU (2) and SU (3) Lie group in the Yang-Mills gauge theory. The groups correspondent to rotations in complex space is rightly the reflection that they describe the motion of spatial quanta that live in another layer which is deeper than that of the real number based detectable particles. The meaning of dimension number in each of the Lie group is now rather trivial, we believe, after the revelation of the underlying physics behind each force. Hereby, all the four fundamental interactions are unified as four aspects of a singular story based on a self-consistent theoretical paradigm, namely the spontaneous symmetry breaking in the space as a binary field.

As for why there are certain errors, though very slight, between the experimental data of baryon masses and our simple calculation, the main contributor should be some minor disturbances by those factors we are not yet able to fully take into consideration at this stage. It is well known that the construction process of the standard model of particle physics was indeed a series of hindsight, through which tens of artificial parameters have been added for the fine tuning with existing experimental data. Therefore, it has good reason to “predict” the outcome of “newly” designed experiments, which are actually nothing but reaffirming the model’s reproductivity by thousands of minorly tinkered versions of similar conditions, without harshly challenging the credibility of it. Luckily enough though, more and more clues have been piling up recently, indicating that the model is far from complete or even correct. Shall we satisfy with a 21^st century version of the Ptolemaic epicycle theory or had we better pursue the possibility of a Copernican revolution (even though not yet sophisticated as Newton or Einstein)? In front us is a vital choice between a self-satisfaction with blind precision and an aesthetic/philosophical awakening.

Now, let us address the pending question we have raised earlier in this paper, namely the entity of the master wave function that governs the entire universe. Our answer is, in the deepest layer of mother nature, there are no laws at all. All regularities or physical laws are nothing but statistically correct patterns or statements. The law of large number and the central limit theorem tell us that even out of a complete randomness, we may still expect certain patterns to appear as far as our sampling procedures are consistent. In other words, order comes not from the nature itself, but instead from the ordered actions of its observers.

It is not abstract mathematics that ultimately governs the universe. “The unreasonable effectiveness of mathematics in the natural sciences”, as admired by Eugene Wigner, in our view, is not because of any divine power of mathematics, but because it is the only language that human can make use of to describe the nature. Some theories of mathematics are proven to be extremely powerful in physical studies, since they happened to share some similarities in their structures with that of the phenomenon in our question.

All successful scientific theories are nothing but a set of self-consistent logical statements, including but not limited to our definition of time and energy. Any theory that first seemed perfect but was later proven to be incomplete, for example the Newtonian mechanics, is because its seemingly perfect logical structure had not met with a test for the hardest challenge yet. For the case of Newtonian mechanics, the problem was that the Galilean transform was not consistent with our definition of time (whereas Lorentz transform was). The invariance of the speed of light rightly complies with our definition of time. As we have reveled in this paper, the velocity of light, as the conversion coefficient between spatial separations and temporal progressions (namely the degree of spatial asymmetry), deservedly has to be constant.

Back to the entity of the master wave of probability density, it is probably no more than an imaginary construct that can best explain, without self-contradiction, all the phenomena that happen on a macroscopic enough scale. In this sense, even the fundamental physical constants may only seem to be invariant as we always measure them with huge enough number of trials. The completely random and stochastic nature of the quantum mechanical world can be alternatively interpreted as if it were the basic constants that are always wandering, vice versa. After all, it is a matter of subjective decision as for how to interpret the nature.

The uncertainty principle tells us that only when we have carried out enough number of trials may we obtain a result with a higher certainty. In his famous book “What is Life”, Erwin Schrodinger had sharply pointed out that all physical laws become reliable only when they are judged by the average behavior of a huge enough number of atoms, which is the very reason why all living creatures have to acquire a certain macroscopic size. A search for the ultimate law of the nature will necessarily end up with “law without law”. It is a conclusion that can be drawn from repetitive rounds of logical reasoning. If we worship a deterministic rule to be the final destination of scientific explorations, then what renders the deterministic character to the rule? The only way to escape from such an endless rat race is to admit Wheeler’s slogan, “law without law”.

Eventually, our newly proposed theoretical paradigm may rephrase the almighty principle of least action as a principle of most probability, which is equivalent to least asymmetry in the space. Physical action has a unit of angular momentum whose conjugate unit in Heisenberg’s uncertainty principle is dimensionless, which could be understood either as an angle or as a probability. In the latter context, the existence of a larger quantum angular momentum is equivalent to a lesser probability of occurrence of such a situation. Thus, the principle of least action is a rephrase of a trivial fact that it is always the event with the highest probability to be the most likely to happen (What a statement of zero b it information).

As the scale of our observation grows up to macroscopic, the predominance of the highest probability becomes more and more overwhelming compared to the second highest in an exponential manner due to the multiplicative nature of probability. Therefore, even a mere probabilistic pattern may well look like a virtually deterministic law.

Unlike the speed of light, and the gravitational constant, the Planck “constant” as a decisive rate limiting factor between deterministic classical physics and probabilistic quantum mechanical world, now has good reasons to be a variable dependent on the size of the universe. A cosmological event horizon that encloses a larger volume may contain more spatial quanta within it (even without the scale factor dependent decrease of the diameter of quanta), thus quite understandably corresponds to a much more deterministic universe. It is rather natural that the Planck scale is a set of evolving standards instead of rigid rulers. Its evolution in accordance with the size or age of the observable universe gratefully frees us from the “mission impossible” to draw specific meaning from the current values of many physical constants or to “glimpse the mind of God” who governs the entire universe.

In response to Einstein’s famous quote “God does not play dice”, Bohr warned him “Don’t tell the God what to do, Einstein.” Today, we have found a better reply: “Yes, you are right, Dr. Einstein, but in the sense that the dicey character of our mother nature is the very proof that there is no God at all.”

Cosmology

It is reasonable to assume that the universe has evolved all the way from a Planck scaled stage to its current state. The fact that our observable universe has a radius ~10⁶⁰ times of Planck length while its energy density is ~10⁻¹²⁰ times of Planck density strongly implies that the effective pressure realized at the cosmological event horizon of our universe shall be structurally fixed by some hitherto unnoticed mechanism at negative 1/3 of its energy density such that the event horizon expands at a constant velocity, namely the speed of light.

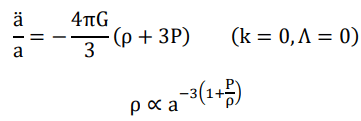
Such a relationship that energy density is proportional to the inverse square (instead of inverse cube) of the radius applies to black holes as well, therefore shall be rather a general feature of phenomena governed by gravity. It is too naïve to believe we are living in a special era when the density of ordinary matter, dark matter and dark energy miraculously meet at roughly the same order.

Note that the integral powers of ~10²⁰ repetitively show themselves in hierarchy problems of fundamental physics. Firstly, ~ 10⁴⁰ is the magnitude gap between gravity and electromagnetism (which is actually a consequence of the very fact that ~10²⁰ itself is the ratio between the Planck mass and the mass of electron or proton). Secondly, ~10⁶⁰ is the multiple of the current Hubble radius, mass and time compared with their Planck scaled counterparts. And lastly, ~10⁸⁰ is the notorious Eddington number.

Instead of asking the reason why the Planck units are so distant from our ordinarily observable realities by those specific magnitudes, or trying to find special meaning for those figures, the right question shall be what kind of a mechanism may assure them to evolve synchronically such that their current values are not special. There were some physicists, with Sir Paul Dirac as the most renowned, who had sought the possibility that some physical constants might actually be time-dependent variables, unfortunately without success to date.

Here we present a hitherto untested hypothesis in which a cosmic scale factor or time-dependent decrease of the Planck constant drives an evolution of the scale of the Planck units and the property of elementary particles (mass and electric charge), which turns out to be able to persuasively solve the most profound conundrums in both cosmology and particle physics at one shot. As a pivotal figure, ~10²⁰ (its precise value is 2.6 × 10²⁰ as will be demonstrate later) is exactly the expansion rate of cosmic scale factor from the very beginning up until today. The evolution of key parameters that characterize our universe are shown in below.

Planck constant

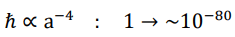
Gravitational constant

G=const.

Speed of light

c=const. (so do ε0 and μ0)

Mass of elementary particles (mass ratio between proton and electron remains constant, mp~1836 me)

Elementary charge

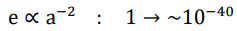
Mass-to-charge ratio of electron and proton

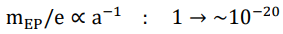
Fine structure constant

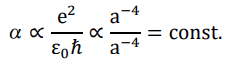
Planck length

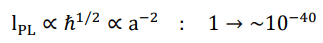
Planck time

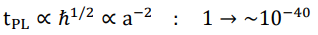
Planck mass

Planck density

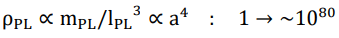
Rydberg constant

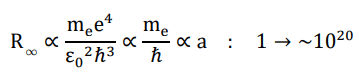
A smaller ydberg “constant” in the past (proportional to cosmic scale factor) implies that the redshift we observe today may not correctly reflect the true expansion of the universe. 1+z has to be re-interpreted downward to its square root.

For example, a seemingly 4-fold redshift (raw z=3) is indeed a spectrum emitted when the Hubble radius was 1/2 of the current length (already “redshifted” by two folds judged by today’s knowledge of spectrometry), being actually redshifted by two folds (true z=1). For small z, by simple math, true redshift shall be 1/2 of raw redshift.

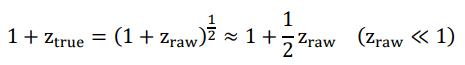
By reducing the Hubble’s constant by 1 (as it is calculated at z << 1), our hypothesis drastically downsized the critical density to 1/4 of its current figure. Such an egg of Columbus solution to the conundrum of the dark energy, of course has a few minor issues to be addressed.

Firstly, how could the weighted average pressure of the various contents of our universe be negative 1/3 of their energy density without the contribution from dark energy. Recall that the pressure of photon gas with a fixed boundary is 1/3 of its energy density. By a reverse logic, the effective pressure realized at a spatial boundary that is expanding at the speed of light (while its constituents remain virtually static to the spatial fabric) should naturally and reasonably be negative 1/3 of the energy density. A good example that a strikingly simple fact can be overlooked for decades.

Secondly, it seems to be rather an overshoot compared with Ω_m~0.315, as the latest estimate by the PLANCK satellite. Note that the above discussion has better affinity with the Cepheid/supernova-based straightforward measurement of the Hubble’s constant, which gives a ~10% larger figure compared with that drawn from the observation of CMB. Should we agree on the matter density (ordinary plus dark) which is confirmed by other methods such as gravitational lensing as well, 10% increase of the Hubble’s constant gives 1% larger critical density that is further subject to the 1 4 reduction, and 0.315/1.21=0.26 is now closer to 0.25.

Lastly, if the universe is expanding at a constant velocity, then a non-linear downward reinterpretation of z_raw to z_true should result in brighter-than-expected supernovae (compared with the theoretical simulation of the redshift luminosity plot in the case of constant velocity expansion) instead of dimmer-than-expected as actually observed, as zraw increases. For example, z_raw=0.1 is equivalent to z_true=0.0488, z_raw=0.2 is equivalent to z_true=0.0954, and 0.0954< 2 × 0.0488. As will be quantitatively explained, the ~20% (+0.2 in luminosity magnitude) dimmer-than-expected supernovae at z_raw ~0.5 are actually due to an underestimate of the Hubble’s constant (as will be demonstrated later, the theoretical value of our observable raw H₀ should be 5[km⁄s/Mpc], with half of this figure as the true rate of expansion). We will also provide a persuasive calculation as for how the supernovae with z_raw>1 turn to be brighter than-expected again, as actually observed.

Recall that

• The spontaneous symmetry breaking in a binary field gives rise to all physical realities;
• The Planck constant evolves with the cosmic scale factor, which further drives the time-dependent evolution of the mass and electric charge of elementary particles,

are the two main pillars of our proposal. Here comes an astounding integration of the two hypotheses. The calculations in below strongly indicate that the big bang was indeed a breaking of equilibrium in which the probability of two quanta flips simultaneously occur was surpassed by the figure of a fractional number of nucleon mass, which was equivalent to the mass of the entire universe back then.

The raw Hubble’s constant from the latest HST result is

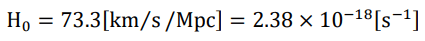
The true Hubble’s constant ( H₀/2) is

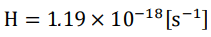
The current Hubble radius is

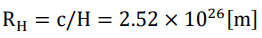
The current mass density of the universe is

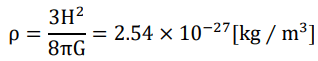
The current Hubble mass is

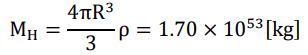
equivalent to 1.02 × 10⁸⁰ times of neutron mass (as the precursor of a proton and an electron through beta decay). Since the Planck length (√2R?) is itself proportional to the inverse square of cosmic scale factor, the cubic root of the ratio between the current Hubble radius and the current R?,

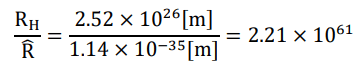
which is 2.80 × 10²⁰, reflecting the true increase of the cosmic scale factor. According to previous discussions, the Eddington number should have increased by a factor of 6.14 × 10⁸¹ (4th power of 2.80 × 10²⁰) from its initial value, thus the initial Eddington number was 1.66 × 10⁻² . On the other hand, the inverse of 2.80 × 10²⁰ is the decreasing factor of the probability density of quanta flip. The current probability density is the inverse square root of the magnitude gap between gravity and electromagnetism of electron-electron interactions, namely the square root of 1/(4.16 × 10⁴²), which is equal to 1/(2.04 × 10²¹). This means the initial probability density should be 1/7.29. And astonishingly,

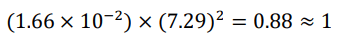
The calculation exactly equals to 1, when

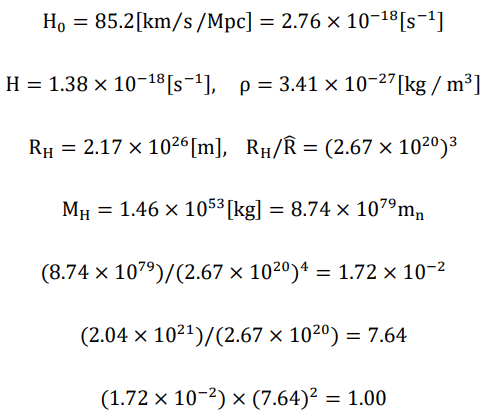
Thus, we have earlier mentioned H₀= 5[km⁄s pc] as the theoretical observable Hubble’s constant. Let us now carry out a quantitative analysis on the luminosity variation of supernovae compared with the theoretical brightness in the case of constant speed expansion (h~0.7).

Firstly, the Chandrasekhar limit remains unchanged in our hypothesis, which assures the mass and absolute luminosity of type-Ia supernovae should be basically time-independent.

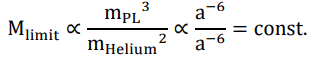
For those supernovae with z_raw ~ 0.5 (z_true ~ 0.225) and h_raw ~ 0.85 or h_true ~ 0.43 (which was wrongly believed to be h_true ~ 0), the luminosity curve we used as theoretical standard was equivalent to z_effective ~ 0.25 and h_raw ~ 0.7, or z_raw ~ 0.5 and h_true ~ 0.35. (Note that we have to down-scale either z_raw or h_raw by one half, to prevent double-count.) The apparent flux is proportional to the inverse square of h × z. Thus, the observed luminosity is ~83.7% of its theoretical standard.

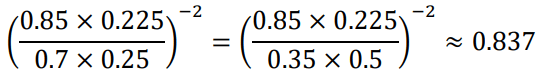
The dimmer-than-expected luminosity shall end at z_raw~1 where the effect of the non-linear revision of z_raw down to ztrue balances with that of the underestimate of H₀.

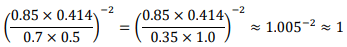
The underestimate of the Hubble’s constant by the HST should be largely due to the intrinsic non-linearity of z_true against z_raw. Since the effect of space expansion is largely hidden by the proper motion of closest supernovae with z_raw ? 1, the redshift-luminosity plots we use to calculate the Hubble’s constant (actually H_raw though) are of those less close supernovae. However, they may already subject to a substantial downside bending, resulting in smaller H_raw.

With such a cosmic scale factor or age-dependent evolution of the mass and charge of electron and nucleons, chemistry should be quite different in ancient universe. It urges us, above all, to reexamine our well-established theory of the Big Bang nucleosynthesis. However, due to our lack of expertise in the field, we would like to rather devote our paper as a priming water for further investigations by qualified experts. Hopefully an upward revision of the baryon-to-photon ratio could better reproduce the observed relative abundance of light elements, which may in turn not only solve the cosmic Lithium problem, but also fill the gap between Ω_b and Ω_m that is currently occupied by dark matter.

As we have seen so far, the origination of energy/mass via spontaneous symmetry breaking in the binary field gives a density proportional to the inverse square of radius in a general manner. It dictates that for any spatial regions of macroscopic enough scales, the mass enclosed within it shall always be proportional to its radius instead of its volume, which may well explain the anomaly of the rotating velocity in galactic arms.

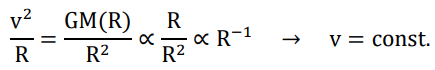
Should the mass of elementary particles evolve with the cosmic age as we have hypothesized, the validity of those cosmological parameters drawn from the observation of CMB needs to be re-examined from scratch. No matter how elaborate or resilient the ΛCD model may look, after all, precision cosmology does not equal to accurate cosmology.

Given that both the energy density of non-relativistic matter and radiation are proportional to the inverse square of the scale factor, there should be no such thing as the “radiation dominant” era in the history of our universe, but instead

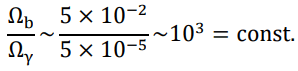
On the other hand, as the universe expands, its temperature should be inversely proportional to the power of /2 of the scale factor, in order to let the energy density of black body radiations

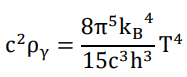
to be proportional to the inverse square of the scale factor. Moreover, the number density of photons shall now be

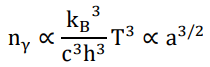
which means the total number of photons increases with the power of 9/2 of the scale factor.

Recall the mass of individual Fermions are proportional to the inverse cube of the scale factor, while their total mass is proportional to the scale factor (since ρ ∝ a⁻²). It implies that the total number of Fermions (and baryons) should be proportional to the 4^th power of the scale factor, which is the very reason why the current Eddington number is ~10⁸⁰ while our universe has only expanded by a factor of ~10²⁰.

Now the baryon-to-photon ratio shall be

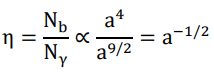
whose initial value should be

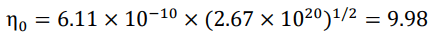
which now settles to a much more reasonable order

Our assumption that the number ratio between matter and photon changes over time is rather natural, considering that both of them are constantly and newly generated via the spontaneous symmetry breaking of the binary field.

Having got rid of the idea of radiation dominant era, plus the increasing number density of both baryons and photons as the universe expands, the CMB radiation should rather be interpreted as a mixture of photons and neutrinos emitted not only during but also right after and even long after the recombination, approximately in a thermal equilibrium. If the CMB is a snapshot of photons at a particular cosmic age without any subsequent interaction with other particles, its temperature shall be inversely proportional to the 5th power of the scale factor (E=hc λ ∝ a⁻⁴/a1=a⁻⁵) instead of a^−7/2. There should be no sharp or qualitative transition from the state of baryon-photon fluid to the so-called dark era, which is a key insight for our discussion hereafter.

With all preparations done, let us recalculate the redshift of the recombination era. The Saha’s ionization equation shall now look like

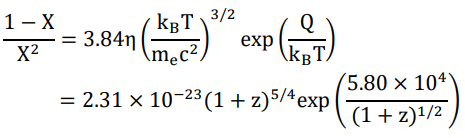
where Q is the binding energy of Hydrogen atoms, which is proportional to the inverse cube of the scale factor, since

Interestingly, there are two solutions that give X=1/2

1+ z = 2.24 × 10¹⁸ and 2.8 × 10⁶

The former is shortly after the birth of the universe, which began with

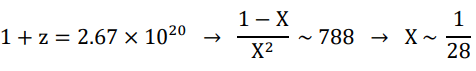
but would have swiftly reached a fully ionized state (X=1) and kept it all the way until 1+z=2.8 × 10⁶, when the recombination occurred.

When 1+z=2.24 × 10¹⁸, the baryon-to-photon ratio η=9.98 × (2.24 × 10¹⁸/2.6 × 10²⁰)^1/2=0.91

was fairly close to 2, which means that all Hydrogen atoms, photons, free protons and free electrons were fully engaged in the reversible reaction.

And here comes a magical show. Recall that our theoretical Hubble’s constant was h=0.426 (half of 0.852), on the other hand, the PLANCK satellite gave h ~ 0.6. It means that our theory implies the critical density of universe to be 40% (= (0.426/0.6)²) of the PLANCK result, where the Ω_b was 0.048 (~1/8 of 40%). Suppose the true baryon to-photon ratio is actually eight times of our current belief, the Saha’s equation will give an initial degree of ionizations

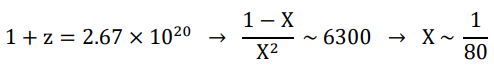
while η₀ ~ 80. It is saying that in the very beginning of our universe, there were on average 9 Hydrogen atoms per one pair of proton and electron and only one Hydrogen atom among them reacts with a photon, which is in equilibrium with its reverse reaction.

The above calculation beautifully explained the asymmetry between the abundance of matter and anti-matter. After all, matter in our definition is nothing but a materialization of a pair of +1 (instead of −1), which was, in the first place, a totally stochastic surplus of perfectly even Bernoulli trials.

If this is not persuasive enough, let us bring out the more decisive one. Recall that we have denied both the snapshot CMB and the termination of the baryon-photon fluid state, which means that the horizon of CMB is always the same with the cosmological event horizon and that the sound wave horizon shall be solely determined by the speed of sound in the baryon-photon fluid.

The energy density of CMB photon is

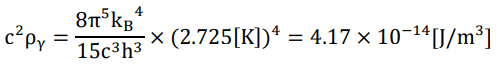
which is equivalent to Ω_γ=5.50 × 10⁻⁵ (h=0.6→ρ_c=8.43 × 10⁻²⁷[kg/m³]), while the energy density of CMB neutrino is

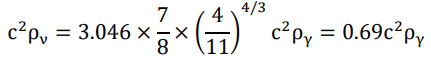
Thus, Ω_radiation=Ω_γ+Ω_ν=1.69 Ω_γ

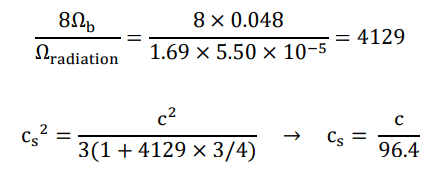
The horizon of the sound waves in the baryon-photon fluid (which is still alive today), if the curvature of our universe is zero, shall have a radius spanning over a visual angle of

1/96.4 [rad]=0.594

On the celestial sphere. The angle is equivalent to l=303 as the theoretical major peak in the TT power spectrum of the CMB, which is, astonishingly, equivalent to observational l ~ 220, exactly as the PLANCK result shows.

Conclusion

In the end, we would like to ask a favor of experimentalists to verify our hypothesis. With 22.9 billion years as the current age of our universe (RH~2.1 × 10²⁶[m]), an experiment measuring the elementary charge over one year should yield a detectable difference in the 9^th digit after the decimal point.

References

1. Wheeler JA. It from bit, 3rd International Symposium of Quantum Mechanics, Tokyo, 1989:354-368.
2. Wheeler JA. Law Without Law, Quantum Theory and Measurement. Princeton University Press, 1983, pp. 182.
3. Diaz RA, Menezes G, Svaiter NF, et al. Spontaneous symmetry breaking in replica field theory. Phys Rev A. 2017;96(6):065012.

   [Crossref] [Google Scholar]

4. Acus A, Malomed BA, Shnir Y. Spontaneous symmetry breaking of binary fields in a nonlinear double-well structure. Physica D: Nonlinear Phenomena. 2012;241(11):987-1002.

   [Crossref] [Google Scholar]

5. Peng R, Fu Q, Chen Y, et al. Spontaneous symmetry breaking in nonlinear binary periodic systems. Phys Rev A. 2024;110(4):043513.

   [Crossref] [Google Scholar]

6. Ochoa F, Clavijo J. Bead, hoop and spring as a classical spontaneous symmetry breaking problem. Eur J Phys. 2006;27(6):1277.

   [Google Scholar]

7. Domokos G, Janson MM, Kovesi-Domokos S. Possible cosmological origin of spontaneous symmetry breaking. Nature. 1975;257(5523):203-205.

   [Crossref] [Google Scholar]

8. Beekman A, Rademaker L, Van Wezel J. An introduction to spontaneous symmetry breaking. SciPost Phys Lect Notes. 2019:011.

   [Google Scholar]

9. Diaz RA, Menezes G, Svaiter NF, et al. Spontaneous symmetry breaking in replica field theory. Phys Rev D. 2017;96(6):065012.

   [Google Scholar]