Review
, Volume: 14( 2)Application of Shoshany-Snodgrass Analysis to the Natario Warp Drive Space time with Zero Expansion
- *Correspondence:
- Fernando Loup*
Department of Physics, University Student Residence Lisbon Portugal, Lisbon, Portugal
E-mail: spacetimeshortcut@yahoo.com
Received: January 25, 2024, Manuscript No. TSSE-24-125912; Editor assigned: January 29, 2024, PreQC No. TSSE-24-125912 March Reviewed: February 13, 2024, QC No. TSSE-24-125912; Revised: March 04, 2025, Manuscript No. TSSE-24-125912(R); Published: March 11, 2024, DOI. 10.37532/2320-6756.2025.14(2).385
Citation: Loup F. Application of Shoshany-Snodgrass Analysis to the Natario Warp Drive Space time with Zero Expansion. J Space Explor. 2025;14(2):385.
Abstract
Alcubierre and Natario developed their warp drives space times using the Arnowitt Arnowitt-DresnerDresner-Misner ADM formalism considering the lapse function α always equal to 1. Recently Barak Shoshany and Ben Snodgrass considered the possibility of warp drive space times in which the lapse function α is different than 1 in very spe cial geometric cases and we arrive at very interesting results: In order to travel to a ”nearby” star at 20 light light-years at superluminal speeds in a reasonable amount of time in months not in years a ship must attain a speed of about 200 times faster than l ight. However, the negative energy density at such a speed is directly proportional to the factor 1048 which is 1.000.000.000.000.000.000.000.000 times bigger in magnitude than the mass of the planet Earth which is” only” proportional to the factor 1024 . The lapse function allows more effectively the negative energy density requirements when a ship travels with a speed of 200 times faster than light using the Shoshany Shoshany-Snodgrass analysis. We reproduce here the Shoshany Shoshany-Snodgrass analysis to the Natario warp drive spacetime with zero expansion.
Keywords
Wave equation; Speed of light; Relativity
Introduction
The warp drive as a solution of the Einstein field equations of general relativity that allows superluminal travel appeared first in 1994 due to the work of Alcubierre [1]. The warp drive as conceived by Alcubierre worked with an expansion of the space time behind an object and contraction of the space time in front. The departure point is being moved away from the object and the destination point is being moved closer to the object. The object does not move at all. It remains at the rest inside the so called warp bubble but an external observer would see the object passing by him at superluminal speeds. Later on in 2001 another warp drive appeared due to the work of Natario [2]. This do not expand or contracts space time but deals with the space time as a” strain” tensor of Fluid Mechanics. Imagine the object being a fish inside an aquarium and the aquarium is floating in the surface of a river but carried out by the river stream. The warp bubble in this case is the aquarium whose walls do not expand or contract. An observer in the margin of the river would see the aquarium passing by him at a large speed but inside the aquarium the fish is at the rest with respect to his local neighborhoods [3-6]. However, there are 3 major drawbacks that compromises the warp drive physical integrity as a viable tool for superluminal interstellar travel. The first drawback is the quest of large negative energy requirements enough to sustain the warp bubble. In order to travel to a “nearby” star at 20 light-years at superluminal speeds in a reasonable amount of time a ship must attain a speed of about 200 times faster than light. However, the negative energy density at such a speed is directly proportional to the factor 1048 which is 1.000.000.000.000.000.000.000.000 times bigger in magnitude than the mass of the planet Earth [7-10].
Another drawback that affects the warp drive is the quest of the interstellar navigation: Interstellar space is not empty and from a real point of view a ship at superluminal speeds would impact asteroids, comets, interstellar space dust and photons.
The last drawback raised against the warp drive is the fact that inside the warp bubble an astronaut cannot send signals with the speed of the light to control the front of the bubble because a Horizon (causally disconnected portion of space time) is established between the astronaut and the warp bubble [11,12].
We can demonstrate that the Natario warp drive can “easily” overcome these obstacles as a valid candidate for superluminal interstellar travel.
Literature Review
In this work we cover only the Natario warp drive and we avoid comparisons between the differences of the models proposed by Alcubierre and Natario since these differences were already deeply covered by the existing available literature. However, we use the Alcubierre shape function to define its Natario counterpart.
Alcubierre M used the so-called 3+1 original Arnowitt-Dresner-Misner (ADM) formalism using the approach of Misner-Thorne-Wheeler (MTW) to develop his warp drive theory. As a matter of fact, the first equation in his warp drive paper is derived precisely from the original 3+1 ADM formalism and we have strong reasons to believe that Natario which followed the Alcubierre steps also used the original 3+1 ADM formalism to develop the Natario warp drive space time [13,14].
The Natario warp drive equation with signature (−, +, +, +) that obeys the original 3+1 ADM formalism is given below:
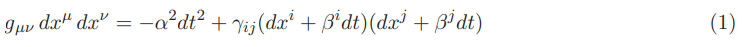
In the equation above α is the so-called lapse function, γij is the 3D diagonal zed induced metric and βi and βj are the so-called shift vectors [4].
Combining the Equations (21.40), (21.42) and (21.44) in (11) with the Equations (2.2.5) and (2.2.6) using the signature (−, +, +, +) we get the original matrices of the 3+1 ADM formalism given by the following expressions:
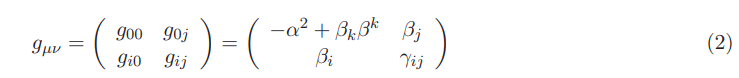
The components of the inverse metric are given by the matrix inverse:
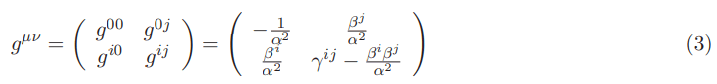
Alcubierre and Natario developed their warp drives considering the lapse function α always equal to 1
Changing the signature from (−, +, +, +) to (+, −, −, −) making α=1 and inserting the components of the Natario vector we have the following equation for the Natario warp drive with zero expansion:
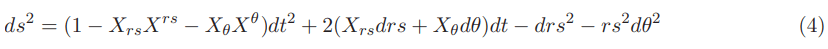
Recently Barak Shoshany and Ben Snodgrass B considered the possibility of warp drive space times in which the lapse function α is different than 1 in very special geometric cases. The equation for the Natario warp drive with zero expansion using a lapse function is given by:
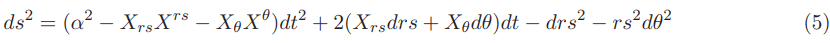
In this work we present the analysis of Barak Shoshany and Ben Snodgrass B adapted to the Natario warp drive with zero expansion using a lapse function and we demonstrate how we arrived at the equation above.
For the study of the original ADM formalism we use the approaches of MTW Misner and Alcubierre and we adopt the Alcubierre convention for notation of equations and scripts.
We adopt here the Geometrized system of units in which c=G=1 for geometric purposes and the International System of units for energetic purposes.
This work is organized as follows:
- Section 2: Introduces the Natario warp drive continuous shape function able to low the negative energy densityrequirements when a ship travels with a speed of 200 times faster than light. The negative energy density for such a speedis directly proportional to the factor 1048 which is 1.000.000.000.000.000.000.000.000 times bigger in magnitude thanthe mass of the planet Earth.
- Section 3: Introduces the Natario warp drive continuous lapse function able to more effectively low the negative energydensity requirements when a ship travels with a speed of 200 times faster than light using the Shoshany-Snodgrass analysisin Shoshany B.
The lapse function possesses the following values:
- Inside the Natario warp bubble where the spaceship resides (flat spacetime) the lapse function is always 1.
- Outside the Natario warp bubble where an external observer resides watching the bubble passing by (also flatspace time) the lapse function is again always 1.
- In the Natario warped region where the derivatives of the Natario shape function are not null (curved space time)the lapse function possesses very large values.
- Section 4: Presents the original equation for the Natario warp drive spacetime with zero expansion and a constant velocityvs without lapse function or with a lapse function always equal to 1 in the original 3+1 ADM formalism in a rigorousmathematical fashion. We recommend the study of the Appendices A and E at the end of the work in order to fullyunderstand the mathematical demonstrations [15].
- Section 5: Presents the original equation for the Natario warp drive spacetime with zero expansion and a constant velocityvs with a large lapse function in the Natario warped region in the original 3+1 ADM formalism in a rigorous mathematicalfashion. We recommend the study of the Appendices I and J at the end of the work in order to fully understand themathematical demonstrations.
- Section 6: Compares all these equations outlining differences and resemblances.
The warp drive as an artificial superluminal geometric tool that allows to travel faster than light may well have an equivalent in the Nature. According to the modern astronomy the universe is expanding and as farther a galaxy is from us as faster the same galaxy recedes from us. The expansion of the Universe is accelerating (see preface of second edition and if the distance between us and a galaxy far and far away is extremely large the speed of the recession may well exceed the light speed limit.
It is very important to note that if a galaxy in the other side of the universe at a billion light-years of distance outside the range of our Particle Horizon is moving away from us at a faster than light speed then superluminal velocities may well exists in nature. So the warp drive may not be impossible at all. Natario also points out exactly this.
What Alcubierre and Natario did was an attempt to reproduce the expansion of the universe in a local way creating a local space time distortion that expands the space time behind a ship and contracts space time in front reproducing the superluminal expansion of the universe moving away the departure point in an expansion and bringing together the destination point in a contraction. The expansion-contraction can be seen in the abs of the original Alcubierre paper. Although Natario says in the abs of his paper in Natario J that the expansion-contraction does not occurs in its space time of the Natario paper we can see the expansion-contraction occurring however the expansion of the normal volume elements or the trace of the extrinsic curvature is zero because the contraction in the radial direction is exactly balanced by the expansion in the perpendicular directions.
An excellent explanation on how a space time distortion or a perturbation pushes away a spaceship from the departure point and brings the ship to the destination point at faster than light speed can be seen in Lobo F. Note that in these works it can be seen that the perturbation does not obeys the time dilatation of the Lorentz transformations hence the speed limit of special relativity cannot be applied here. An accelerated warp drive can only exist if the astronaut in the center of the warp bubble can somehow communicate with the warp bubble walls sending instructions to change its speed. But for signals at light speed the Horizon exists so light speed cannot be used to send signals to the front of the bubble. Besides in the Natario warp drive the negative energy density covers the entire bubble. Since the negative energy density have repulsive gravitational behavior the photon of light if possible to reach the bubble walls would then be deflected by the repulsive behavior never reaching the bubble walls.
The solution that allows contact with the bubble walls was presented in Loup F. Although the light cone of the external part of the warp bubble is causally disconnected from the astronaut who lies inside the large bubble he (or she) can somehow generate micro warp bubbles and since the astronaut is external to the micro warp bubble he (or she) contains the entire light cone of the micro bubble so these bubbles can be” engineered” to be sent to the large bubble. This idea seems to be endorsed by Lobo F where it is mentioned that warp drives can only be created or controlled by an observer that contains the entire forward light cone of the bubble. See also an important point of view in Lobo F.
This work covers only the lapse function for the Natario warp drive with zero expansion at a constant velocity.
But for the case of the warp drive equations with variable velocities we still do not have geometries possessing a lapse function α. This(perhaps) will be done in future works [16].
Although this work was written to be independent self-contained and self-consistent it must be regarded as a companion work to our works in Loup F.
The Natario warp drive continuous shape function
Introducing here f(rs) as the Alcubierre shape function that defines the Alcubierre warp drive space time we can construct the Natario shape function n(rs) that defines the Natario warp drive space time using its Alcubierre counterpart. Below is presented the equation of the Alcubierre shape function [5].
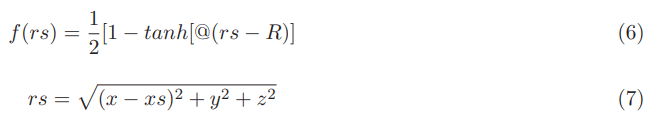
According with Alcubierre any function f(rs) that gives 1 inside the bubble and 0 outside the bubble while being 1>f(rs)>0 in the Alcubierre warped region is a valid shape function for the Alcubierre warp drive.
In the Alcubierre shape function xs is the center of the warp bubble where the ship resides. R is the radius of the warp bubble and @ is the Alcubierre parameter related to the thickness. According to Alcubierre these can have arbitrary values. We outline here the fact that according to the parameter @ can have arbitrary values.rs is the path of the so-called Eulerian observer that starts at the center of the bubble xs=R=rs=0 and ends up outside the warp bubble rs>R.
According to Natario any function that gives 0 inside the bubble and 1/2 outside the bubble while being 0<n(rs)<1/2 in the Natario warped region is a valid shape function for the natario warp drive
The Natario warp drive continuous shape function can be defined by:
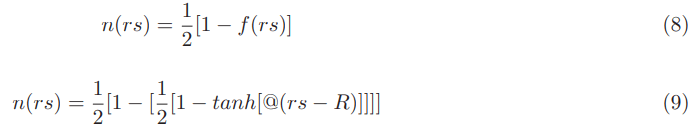
This shape function gives the result of n(rs)=0 inside the warp bubble and n(rs)=1/2 outside the warp bubble while being 0
Note that the Alcubierre shape function is being used to define its Natario shape function counterpart [17].
For the Natario shape function introduced above it is easy to figure out when f(rs)=1(interior of the Alcubierre bubble) then n(rs)=0(interior of the Natario bubble) and when f(rs)=0(exterior of the Alcubierre bubble) then n(rs)=1/2 (exterior of the Natario bubble).
Another Natario warp drive valid shape function can be given by:

Its derivative square is:
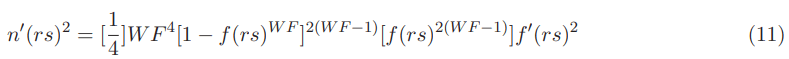
The shape function above also gives the result of n(rs)=0 inside the warp bubble and n(rs)=1/2 outside the warp bubble while being 0
Note that like in the previous case the Alcubierre shape function is being used to define its Natario shape function counterpart. The term W F in the Natario shape function is dimensionless too: It is the warp factor. It is important to outline that the warp factor W F >> |R| is much greater than the modulus of the bubble radius [18].
For the second Natario shape function introduced above it is easy to figure out when f(rs)=1(interior of the Alcubierre bubble) then n(rs)=0(interior of the Natario bubble) and when f(rs)=0(exterior of the Alcubierre bubble) then n(rs)=1/ 2 (exterior of the Natario bubble).
Numerical plot for the second shape function with @=50000 R=100 meters and warp factor with a value WF=200
| rs | f(rs) | n(rs) | f'(rs)2 | n'(rs)2 |
| 9, 99970000000E+001 | 1 | 0 | 2, 650396620740E-251 | 0 |
| 9, 99980000000E+001 | 1 | 0 | 1, 915169647489E-164 | 0 |
| 9, 99990000000E+001 | 1 | 0 | 1, 383896564748E-077 | 0 |
| 1, .00000000000E+002 | 0,5 | 0,5 | 6, 250000000000E+008 | 3, 872591914849E - 103 |
| 1,00001000000.E+002 | 0 | 0,5 | 1, 383896486082E-077 | 0 |
| 1, 00002000000E+002 | 0 | 0,5 | 1, 915169538624E-164 | 0 |
| 1, 00003000000E+002 | 0 | 0,5 | 2, 650396470082E 251 | 0 |
Numerical plot for the second shape function with @=75000 R=100 meters and warp factor with a value WF=200
| rs | f(rs) | n(rs) | f'(rs)2 | n'(rs)2 |
| 9, 99980000000E + 001 | 1 | 0 | 5, 963392481410E 251 | 0 |
| 9, 99990000000E + 001 | 1 | 0 | 1, 158345097767E 120 | 0 |
| 1,00000000000E + 002 | 0,5 | 0,5 | 1, .406250000000E + 009 | 8, .713331808411E 103 |
| 1,00001000000E + 002 | 0 | 0,5 | 1, 158344999000E - 120 | 0 |
| .00002000000E + 002 | 0 | 0,5 | 5, 963391972940E - 251 | 0 |
Numerical plot for the second shape function with @=100000 R=100 meters and warp factor with a valueWF=200
| rs | f (rs) | n(rs) | f'(rs)2 | n'(rs)2 |
| 9. 99990000000E + 001 | 1 | 0 | 7, 1.660678807684E - 164 | 0 |
| 1,00000000000E + 002 | 0,5 | 0,5 | 2, 500000000000E + 009 | 1.549036765940E-102 |
| 1,00001000000E + 002 | 0 | 0,5 | 7. 660677936765E - 164 | 0 |
The plots in the previous page demonstrate the important role of the thickness parameter @ in the warp bubble geometry wether in both Alcubierre or Natario warp drive space times. For a bubble of 100 meters’ radius R=100 the regions where 1>f(rs)>0(Alcubierre warped region) and 0
As large as @ becomes as smaller ∈ becomes too.
- The geometrized warped region where 1>f(rs)>0 (Alcubierre warped region) and 0
- The energized warped region where the derivative squares of both Alcubierre and Natario shape functions are not zero.
The energized warped region where the derivative squares of both Alcubierre and Natario shape functions are not zero.
The parameter @ affects both energized warped regions wether in Alcubierre or Natario cases but is more visible for the Alcubierre shape function because the warp factor W F in the Natario shape functions squeezes the energized warped region into a very small thickness [19].
The negative energy density for the Natario warp drive is given.
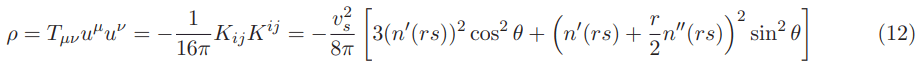
Converting from the Geometrized system of units to the international system we should expect for the following expression (see Appendix G):
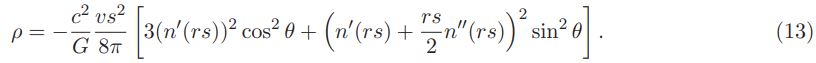
Rewriting the Natario negative energy density in cartezian coordinates we should expect for (see Appendix D):
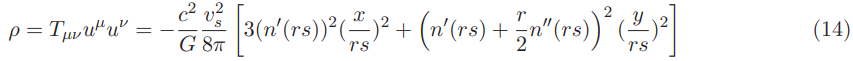
In the equatorial plane (1+1 dimensional spacetime with rs=x−xs, y=0 and center of the bubble xs = 0):
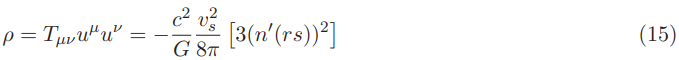
Note that in the above expressions the warp drive speed vs appears raised to a power of 2. Considering our Natario warp drive moving with vs=200 which means to say 200 times light speed in order to make a round trip from Earth to a nearby star at 20 light-years away in a reasonable amount of time(in months not in years) we would get in the expression of the negative energy the factor c2=(3 × 108)2=9 × 1016 being divided by 6, 67 × 10−11 giving 1, 35 × 1027 and this is multiplied by (6 × 1010)2=3, 6 × 1020 coming from the term vs=200 giving 1, 35 × 1027 × 36 × 1020=1, 35 × 1027 × 3, 6 × 1021=4, 86 × 1048 !!!
A number with 48 zeros. The planet Earth have a mass6 of about 6 × 1024 kg
This term is 1.000.000.000.000.000.000.000.000 times bigger in magnitude than the mass of the planet Earth or better: The amount of negative energy density needed to sustain a warp bubble at a speed of 200 times faster than light requires the magnitude of the masses of 1.000.000.000.000.000.000.000.000 planet Earths.
Note that if the negative energy density is proportional to 1048 this would render the warp drive impossible but fortunately the square derivative of the Natario shape function possesses values of 10-102 ameliorating the factor 1048 making the warp drive negative energy density more affordable. For a detailed study of the derivatives of first and second order of the Natario shape function n(rs).
The Natario warp drive continuous lapse function
In the previous section we presented the Natario warp drive continuous shape function defined using the equation of the Alcubierre shape function [7].

The Natario warp drive continuous shape function is defined as being:

The expression for the first order derivative of the Natario shape function is:
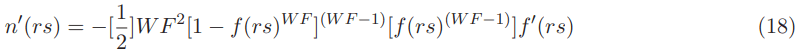
Its derivative square is:
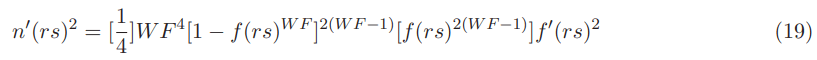
With the first order derivative of the Alcubierre shape function being:
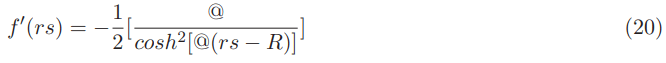
The term W F in the Natario shape function is dimensionless: It is the warp factor. It is important to outline that the warp factor W F >> |R| is much greater than the modulus of the bubble radius.
In the Alcubierre shape function xs is the center of the warp bubble where the ship resides. R is the radius of the warp bubble and @ is the Alcubierre parameter related to the thickness. According to Alcubierre these can have arbitrary values. We outline here the fact that according the parameter @ can have arbitrary values.rs is the path of the so-called Eulerian observer that starts at the center of the bubble xs=R=rs=0 and ends up outside the warp bubble rs>R.
According to Natario any function that gives 0 inside the bubble and 1/2 outside the bubble while being 0
For the Natario shape function introduced above it is easy to figure out when f(rs)=1(interior of the Alcubierre bubble) then n(rs)=0(interior of the Natario bubble) and when f(rs)=0(exterior of the Alcubierre bubble) then n(rs)=1/2 (exterior of the Natario bubble).
We introduce here the Natario warp drive continuous lapse function with a value equal to 1 in the regions inside and outside the Natario bubble while having large values in the Natario warped region. The Natario warp drive continuous lapse function is given by;
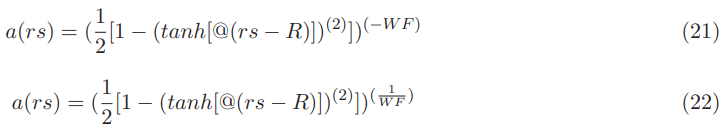
Its square is then given by: (see Appendix I for details)
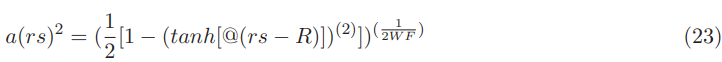
| rs | a(rs) | a (rs)2 | n' (rs) |
| 9. 999500000000E+00 | 1, 000000000000E+000 | 1, 100000000000000E+000 | 0. 00000000000E+000 |
| 9. 1999600000000E+00 | 1, .000000000000E+000 | 1,00000000000000E+000 | 0. .00000000000E+000 |
| 9. .999700000000E+00 | 1. .000000000037E+000 | 1. .00000000007487E+000 | 0.00000000000E+000 |
| 9.999800000000E+00 | 1. 000000824462E+000 | 1. 00000164892427.E+000 | 0.00000000000E+000 |
| 9.999900000000E+00 | 1. 018325027378E+000 | 1, 03698586138517E+000 | 0,00000000000E+000 |
| .000000000000E+01 | 1. 606938044259E+060 | 2. 58224987808691+120 | 6.22301527786E-052 |
| 1.000010000000E+01 | 1, 018325027273E+000 | 1, 13698586117111E+000 | 0.00000000000E+000 |
| 1.000020000000E+01 | 1.000000824462E+000 | 1. .00000164892427E+000 | 0.00000000000E+000 |
| 1.000030000000E+01 | 1.000000000037.E+000 | 1. .00000000007487. E+000 | 0.00000000000E+000 |
| .000040000000E+01 | 1. .000000000000E+000 | 1. .00000000000000+000 | 0,00000000000E+000 |
| 1.000050000000E+01 | 1. .000000000000E+000 | 1. .00000000000000+000 | 0.00000000000E+000 |
| rs | a(rs) | a(rs)2 | n'(rs)2 |
| 9. 999500000000E+00 | 1. 000000000000E+000 | 1. 100000000000000E+000 | 0.00000000000E+000 |
| 9. .999600000000E+00 | 1. 000000000000E+000 | 1, .0000000000000+000 | 0.00000000000E+000 |
| 9. .999700000000E+00 | 1. .000000000037E+000 | 1.00000000007487E+000 | 0.00000000000E+000 |
| 9.999800000000E+00 | 1. 000000824462E+000 | 1. 100000164892427E+000 | 0.00000000000E+000 |
| 9.999900000000E+00 | 1. 018325027378E+000 | 1, 13698586138517E+000 | 0.00000000000E+000 |
| 1.000000000000E+01 | 1. 606938044259E+060 | 2. 58224987808691E+120 | 3.8725919148493E-103 |
| 1.000010000000E+01 | 1.018325027273E+000 | 1. .03698586117111E+000 | 0.00000000000E+000 |
| 1.000020000000E+01 | 1. .000000824462E+000 | 1.00000164892427F+000 | 0.00000000000E+000 |
| 1.000030000000E+01 | 1. .000000000037E+000 | 1. 100000000007487. E+000 | 0.00000000000E+000 |
| 1.000040000000E+01 | 1. 000000000000E+000 | 1. .00000000000000E+000 | 0.00000000000E+000 |
| 1.000050000000E+01 | 1. .000000000000E+000 | 1.00000000000000E+000 | 0.00000000000E |
Above are presented the numerical plots for the Natario warp drive continuous lapse function its square and the first order derivative and also its square of the Natario warp drive continuous shape function with @=50000 R=100 meters and warp factor with a value WF=2008. The values of the Natario warp drive continuous lapse function and its square are equal to 1 inside and outside the Natario bubble while having large values in the Natario warped region.
The derivative of the Natario warp drive continuous shape function and its square have very low values in the Natario warped region. The extrinsic curvatures are essential to calculate the negative energy density requirements. Below are presented the extrinsic curvatures for the Natario warp drive without a lapse function or with a lapse function always equal. see also Appendix B for details.
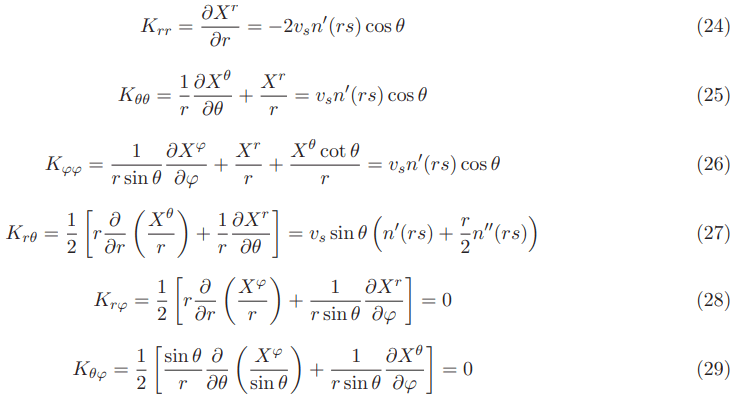
The expansion of the normal volume elements is zero and given by:

Below are presented the extrinsic curvatures for the Natario warp drive with a lapse function that is 1 in the regions inside and outside the Natario bubble while being large in the Natario warped region. See Appendix I for details [9].
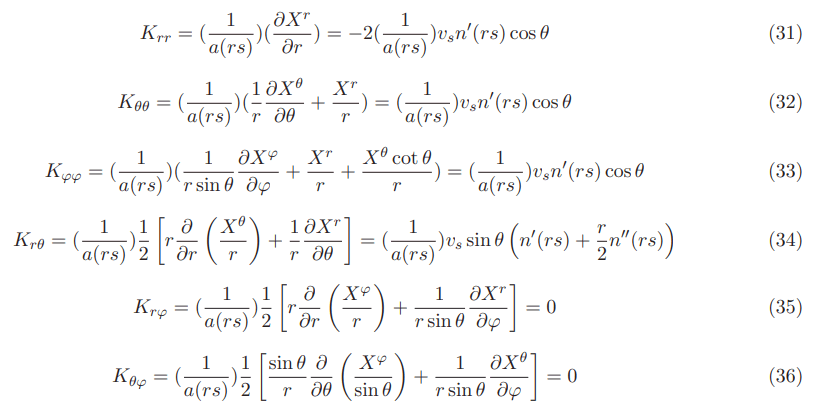
For the case of the extrinsic curvatures without a lapse function the dominant terms are the bubble speed vs and the derivatives of the Natario shape function n ′ (rs) and n ′′(rs). The first order derivative of the Natario shape function is zero inside and outside the bubble while having a very low value 10-52in the Natario warped region. This is crucial to low the negative energy density requirements as shown in the previous section. Independently of the system of units being used wether in the SI or MKS or the Geometrized System G=c=1 a speed vs of about 200 times faster than light with an order of magnitude of about 1021 or 1048 would be completely obliterated by the factor 10-52of the Natario shape function first order derivative. For a detailed study of the derivatives of first and second order of the Natario shape function n(rs).
But for the case of the extrinsic curvatures with a lapse function that is 1 in the regions inside and outside the Natario bubble while having a large value in the Natario warped region we have an extra factor. The lapse function has a value of 1060 in the Natario warped region and 1 a(rs) have a value of 10−60 contributing also to obliterate the factor 10-20 or 10
The equations of the negative energy density in the Natario warp drive space time given in function of the extrinsic curvatures are the following ones:
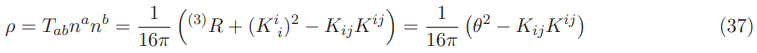
Since the trace of the extrinsic curvatures or the expansion of the normal volume elements is zero θ=Krr+Kθθ+K??=0 then (Kii)2=θ 2=0 and (3) R=0 the equation reduces to:
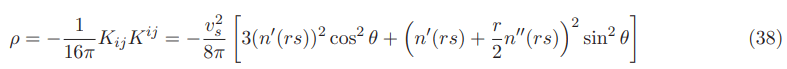
The equation above is the negative energy density without lapse function or for a lapse function that is 1 everywhere. For a lapse function that is 1 inside and outside the Natario warp bubble but possessing very large values in the Natario warped region the corresponding equation would then be: (Appendix I for details)
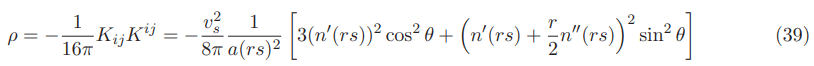
The equations are being given in the Geometrized system of units G=c=1 but wether in this system or the SI or MKS System of units the lapse function helps to reduce the negative energy density requirements in the Natario warp drive space time. Note that the factor 1/a(rs)2=1/10-120=10-120 thereby reducing effectively the factor 10-21 or 1048 from a speed of 200 times faster than light.
Discussion
The equation of the Natario warp drive space time metric with a constant speed vs in the original 3+1 ADM formalism without a lapse function or using a lapse function always equal to 1 everywhere.
The equation of the Natario warp drive space time in the original 3+1 ADM formalism is given by: (see Appendix E for details)
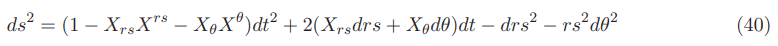
The equation of the Natario vector nX is given by:

With the contravariant shift vector components Xrs and Xθ given by: (see also Appendix A for details)
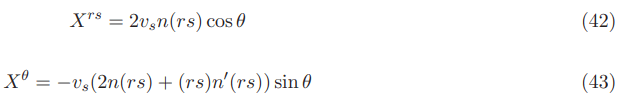
The covariant shift vector components Xrs and Xθ are given by:
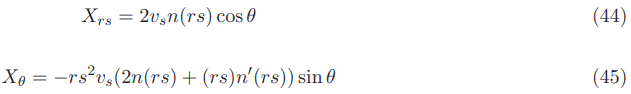
Considering a valid n(rs) as a Natario shape function being n(rs)=1/2 for large rs (outside the warp bubble) and n(rs)=0 for small rs(inside the warp bubble) while being 0
We must demonstrate that the Natario warp drive equation given above satisfies the Natario requirements for a warp bubble defined by:
Any Natario vector nX generates a warp drive space time if nX=0 and X=vs=0 for a small value of rs defined by Natario as the interior of the warp bubble and nX=vs(t)dx with X=vs for a large value of rs defined by Natario as the exterior of the warp bubble with vs(t) being the speed of the warp bubble.
Natario in its warp drive uses the spherical coordinates rs and θ. In order to simplify our analysis, we consider motion in the x−axis or the equatorial plane rs where θ=0 sin(θ)=0 and cos(θ)=1.
In a 1+1 space time the equatorial plane we get:
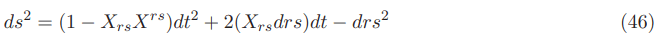
The equation above was written using both contravariant and covariant shift vector components of the Natario vector at the same time.
Since Xrs= Xrs the equation in the 1+1 space time can be written as given below:
Contravariant form; all the shift vector components of the Natario vector are contravariant
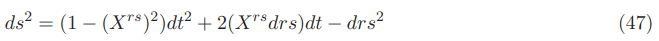
Covariant form: all the shift vector components of the Natario vector are covariant
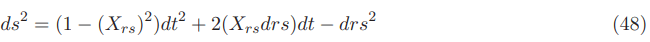
The equal contravariant and covariant shift vector component Xrs and Xrs are then:

Remember that Natario defines the x axis as the axis of motion. Inside the bubble n(rs)=0 resulting in a Xrs=0 and outside the bubble n(rs)=1/2 resulting in a Xrs=vs and this illustrates the Natario definition for a warp drive space time.
The equation of the Natario warp drive space time metric with a constant speed vs in the original 3+1 ADM formalism using a lapse function α always equal to 1 in the regions inside and outside the Natario bubble but with large values in the Natario warped region.
The equation of the Natario warp drive space time in the original 3+1 ADM formalism is given by: (Appendix J for details)
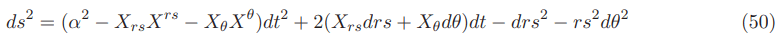
This section is almost similar to the previous section with the Natario vector and the Natario shape function being equal to their counterparts of the previous section however with a difference: the lapse function α
In a 1+1 space time the equatorial plane we get:
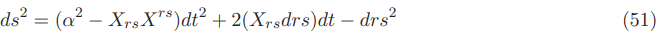
The equation above was written using both contravariant and covariant shift vector components of the Natario vector at the same time.
Since Xrs=Xrs the equation in the 1+1 spacetime can be written as given below:
Contravariant form; All the shift vector components of the Natario vector are contravariant
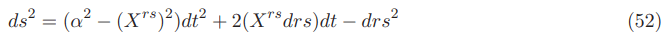
Covariant form: All the shift vector components of the Natario vector are covariant
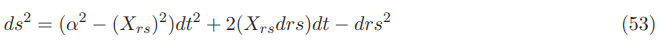
The equal contravariant and covariant shift vector component Xrs and Xrs are then:

Remember that Natario defines the x axis as the axis of motion. Inside the bubble n(rs)=0 resulting in a Xrs=0 and outside the bubble n(rs)=1/2 resulting in a Xrs=vs and this illustrates the Natario definition for a warp drive space time.
Differences and resemblances between all these equations with or without lapse function in the original 3+1 ADM formalism for the Natario warp drive space time
The equation in 3+1 original ADM formalism for the Natario warp drive space time for a constant velocity vs without a lapse function or with a lapse function that is always 1 everywhere is given by: (Appendices A and E for details)
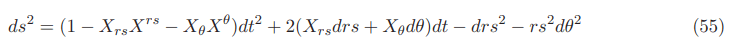
The equation in 3+1 original ADM formalism for the Natario warp drive spacetime for a constant velocity vs with a lapse function that is always 1 inside and outside the Natario bubble but with a large value in the Natario warped region is given by: (Appendix J for details)
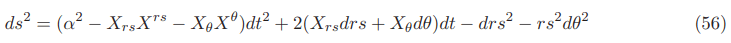
Placing both equations side by side one can easily see that the relevant difference between these equations is precisely the lapse function α or in this case α2.
While the Natario vector or the Natario shape function is the same for both equations the presence of a non-unit lapse function α or in this case α
Inside the Natario bubble where the spaceship resides (flat space time) the first equation have 1 in the place of the lapse function and the second equation have a lapse function equal to 1 so here we have no differences after all.
Outside the Natario bubble where an external observer resides watching the bubble passing by (also flat space time) the first equation again have 1 in the place of the lapse function and the second equation have a lapse function again equal to 1 so here we have no differences after all.
But in the Natario warped region where the derivatives of the Natario shape functions are non-null (curved space time) the presence of a large lapse function affects the spacetime geometry and hence the negative energy density of the second case.
The negative energy density for the Natario warp drive in the original 3+1 ADM formalism without lapse function or with a lapse function always equal to 1 for fixed velocities in the International System of Units SI (Appendix G) is given.
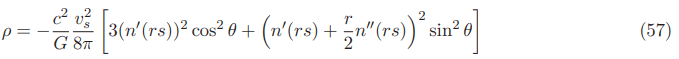
In the equatorial plane (1+1 dimensional spacetime with rs=x−xs, y=0 and center of the bubble xs=0) the negative energy density for fixed velocities is given by: (see Appendix D)
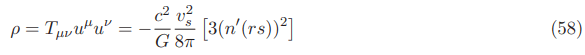
The negative energy density for the Natario warp drive in the original 3+1 ADM formalism with a large lapse function for fixed velocities in the International System of Units SI (Appendices G, I and Section 3) is given.
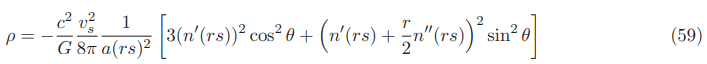
In the equatorial plane (1+1 dimensional spacetime with rs=x−xs, y=0 and center of the bubble xs=0) the negative energy density for fixed velocities is given by: (Appendices D and I)
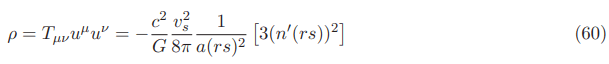
Wither in the 3+1 or 1+1 space times the first equation does not possess the factor 1/a(rs)2 but the second equation possesses this factor. A large lapse function reduces the negative energy density requirements in the second case.
Note that in both equations the negative energy density requirements even in the equatorial plane is not null The negative energy density have repulsive gravitational behavior and is distributed along all the bubble volume even in the equatorial plane so any hazardous incoming objects in front of the bubble (Doppler blueshifted photons or space dust or debris) would then be deflected by the repulsive behavior of the negative energy in front of the bubble never reaching the bubble walls [10].
But for the case of the warp drive equations with variable velocities wether the lapse function a(rs) is 1 or not we can say nothing about the negative energy density at first sight and we need to compute “all-the-way-round” the Christoffel symbols Riemann and Ricci tensors and the Ricci scalar in order to obtain the Einstein tensor and hence the stress-energy-momentum tensor in a long and tedious process of tensor analysis liable of occurrence of calculation errors. Or we can use the techniques described in the Appendix I using extrinsic curvatures and shift vectors but still subject to computation errors.
Or we can use computers with programs like M aple or M athematica.
Appendix C shows how to calculate everything until the Einstein tensor from the basic input of the covariant components of the 3 +1 space time metric using Mathematica.
Also Barak Shoshany and Ben Snodgrass used OGRe for M athemathica and OGReP y for P ython to compute relevant tensor calculations.
But since the Natario shape function n(rs) is the same for all these equations it is reasonable to suppose that derivatives of first second(or perhaps higher)order will appear in the negative energy density expression for the Natario warp drive with variable velocity and since the derivatives of first or second order for the Natario shape function possesses extremely low values these values can obliterate large terms for velocities vs or large accelerations a.For a detailed study of the derivatives of first and second order of the Natario shape function n(rs).
Conclusion
In this work borrowed the ideas of Barak Shoshany and Ben Snodgrass and we presented a continuous and differentiable lapse function α for the Natario warp drive with zero expansion in Natario J.
Our expression for α is given by:
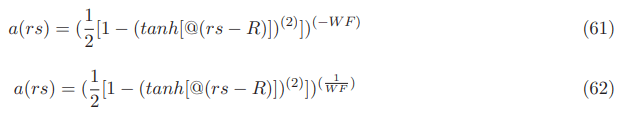
This expression for the lapse function α was constructed using the Alcubierre and Natario shape functions as inspirations and possesses a very interesting behavior:
- Inside the Natario warp bubble where the spaceship resides (flat spacetime) the lapse function is always 1.
- Outside the Natario warp bubble where an external observer resides watching the bubble passing by (also flat space time)the lapse function is again always 1.
- In the Natario warped region where the derivatives of the Natario shape function are not null (curved space time) the lapsefunction possesses very large values.
Our choice for the Natario shape function is given by:

Its derivative square is:
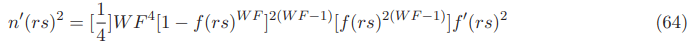
The shape function above gives the result of n(rs)=0 inside the warp bubble and n(rs)=1/2 outside the warp bubble while being 0
Considering a Natario warp drive moving with vs=200 which means to say 200 times faster than light in order to make a round trip from Earth to a nearby star at 20 light-years away in a reasonable amount of time(in months not in years) and since the negative energy density ia proportional to the factor c
A number with 48 zeros!!!The planet Earth have a mass [11] of about 6 × 1024kg
This term 1048 is 1.000.000.000.000.000.000.000.000 times bigger in magnitude than the mass of the planet Earth!!!or better: The amount of negative energy density needed to sustain a warp bubble at a speed of 200 times faster than light requires the magnitude of the masses of 1.000.000.000.000.000.000.000.000 planet Earths.
Note that if the negative energy density is proportional to 1048 this would render the warp drive impossible but fortunately the square derivative of our choosed Natario shape function possesses values of 10−102 (as we have shown in section 2) ameliorating the factor 1048 making the warp drive negative energy density more” affordable”. For a detailed study of the derivatives of first and second order of the Natario shape function n(rs).
The equation in 3+1 original ADM formalism for the Natario warp drive spacetime for a constant velocity vs with a lapse function that is always 1 inside and outside the Natario bubble but with a large value in the Natario warped region is given by:(see Appendix J for details)
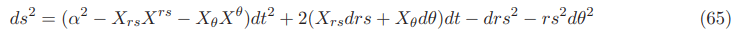
The negative energy density for the Natario warp drive in the original 3+1 ADM formalism with a large lapse function for fixed velocities in the International System of Units SI (see Appendices G, I and Section 3) is given.
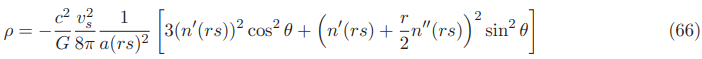
Our lapse function that is 1 in the regions inside and outside the Natario bubble while having a large value in the Natario warped region possesses an an extra factor. The lapse function have a value of 1060 in the Natario warped region and 1/a(rs) have a value of 10−60 contributing also to obliterate the factor 1048. Note that the negative energy density incorporates the factor 1/a(rs)2=1/ 10120=10−120 thereby reducing effectively the factor 1048 from a speed of 200 times faster than light (as we have shown in section 3).
In the equatorial plane (1+1 dimensional spacetime with rs=x−xs, y=0 and center of the bubble xs=0) the negative energy density is given by:(see Appendices D and I)
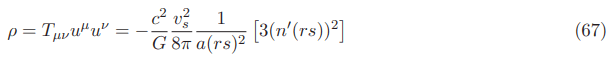
Note that the negative energy density requirements even in the equatorial plane is not null The negative energy density have repulsive gravitational behavior and is distributed along all the bubble volume even in the equatorial plane so any hazardous incoming objects in front of the bubble (Doppler blueshifted photons or space dust or debris) would then be deflected by the repulsive behavior of the negative energy in front of the bubble never reaching the bubble walls [12].
A real and fully functional warp drive must encompass accelerations or de-accelerations in order to go from 0 to 200 times light speed in the beginning of an interstellar journey and to slow down to 0 again in the end of the interstellar journey. But for the case of the warp drive equations with variable velocities we still do not have geometries possessing a lapse function α. This(perhaps) will be done in future works.
Because collisions between the walls of the warp bubble and the hazardous particles of the Interstellar Medium (IM) would certainly occurs in a real superluminal interstellar spaceflight we borrowed the more than welcome idea of Chris Van Den Broeck proposed some years ago in 1999 in order to increase the degree of protection of the spaceship and the crew members in the Natario warp drive equation for constant speed.
Our idea was to keep the surface area of the bubble exposed to collisions microscopically small avoiding the collisions with the dangerous IM particles while at the same time expanding the spatial volume inside the bubble to a size larger enough to contains a spaceship inside.
A submicroscopic outer radius of the bubble being the only part in contact with our Universe would mean a submicroscopic surface exposed to the collisions against the hazardous IM particles thereby reducing the probabilities of dangerous impacts against large objects (comets asteroids etc.) enhancing the protection level of the spaceship and hence the survivability of the crew members.
Any future development for the Natario warp drive must encompass the more than welcome idea of Chris Van Den Broeck and this idea can also be easily implemented in the Natario warp drive with a lapse function. Since the Broeck idea is independent of the Natario geometry possessing a lapse function we did not covered the Broeck idea here because it was already covered in Loup F and Broeck C and in order to discuss the geometry of a Natario warp drive with a lapse function the Broeck idea is not needed here however the Broeck idea must appear in a real Natario warp drive a lapse function concerning realistic superluminal interstellar spaceflights.
But unfortunately although we can discuss mathematically how to reduce the negative energy density requirements to sustain a warp drive we do not know how to generate the shape function that distorts the spacetime geometry creating the warp drive effect. And we also so not know how to generate the lapse function either. So unfortunately all the discussions about warp drives are still under the domain of the mathematical conjectures.
However, we are confident to affirm that the Natario-Broeck warp drive will survive the passage of the Century XXI and will arrive to the Future. The Natario-Broeck warp drive as a valid candidate for faster than light interstellar space travel will arrive to the the Century XXIV on-board the future starships up there in the middle of the stars helping the human race to give his first steps in the exploration of our Galaxy.
References
- Alcubierre M. The warp drive: hyper-fast travel within general relativity. Class Quantum Grav. 1994;11(5): L73.
- Natário J. Warp drive with zero expansion. Class Quantum Grav. 2002;19(6):1157.
- Warnick KF. Teaching electromagnetic field theory using differential forms. In Teaching Electromagnetics 2021(pp. 129-164). CRC Press.
- Misner KS. Thorne and JA Wheeler. Gravitation, (Ed. Freeman, San Francisco, 1973). 1973.
- Alcubierre M. Introduction to 3+ 1 numerical relativity. OUP Oxford; 2008.
- Schutz B. A first course in general relativity. Cambridge university press; 2022.
- Ryder L. Introduction to general relativity. Cambridge University Press; 2009.
- Van Den Broeck C. Awarp drive'with more reasonable total energy requirements. Class Quantum Grav. 1999;16(12):3973.
- Lobo FS. Exotic solutions in General Relativity: Traversable wormholes and'warp drive'spacetimes. Nova Sci Pub. 2008: 1-78.
- Lobo FS. Wormholes, warp drives and energy conditions. Berlin: Springer; 2017.
- Wald RM. General relativity. the university of Chicago. Chicago. Sect. 1984;6:3840.
- Rindler W. Relativity: special, general, and cosmological. OUP Oxford; 2006 Apr 7.
- Plebanski J, Krasinski A. An introduction to general relativity and cosmology. Cambridge University Press; 2024 Jun 6.
- Everett A, Roman T. Time travel and warp drives: a scientific guide to shortcuts through time and space. University of Chicago Press; 2012.
- Dalarsson M, Dalarsson N. Tensors, relativity, and cosmology. Academic Press; 2015.
- Natario J. Warp Drive Seminar Lectures. Instituto Superior Tecnico, Lisboa Portugal. 2003.
- Shoshany B, Snodgrass B. Warp Drives, Rest Frame Transitions, and Closed Timelike Curves. arXiv preprint arXiv:2309.10072. 2023.
- Shoshany B. Lectures on faster-than-light travel and time travel. Sci Post Physics Lecture Notes. 2019:010.
- Baumgarte TW, Shapiro SL. Numerical relativity: solving Einstein's equations on the computer. Cambridge University Press; 2010.

