Original Article
, Volume: 6( 1)The Processes of Energy/Momentum Exchange for Rotating Plasma Flows in Crossed External Fields
1Russia Department of Electrophysical Facilities, National Research Nuclear University MEPhI, Kashirskoye Shosse 31, Moscow, Russia
2Morningstar Applied Physics, LLC Vienna, VA 22182, USA
- *Correspondence:
- Karimov AR , Russia Department of Electrophysical Facilities, National Research Nuclear university MEPhI, Kashirskoye Shosse 31, Moscow, 115409, Russia,Tel: +74991357760; E-mail:alexanderkarimov999@gmail.com
Received: December 07, 2016; Accepted: February 16, 2017; Published: February 23, 2017
Citation: Karimov AR, Murad PA. The Processes of Energy/Momentum Exchange for Rotating Plasma Flows in Crossed External Fields. J Space Explor. 2017;6(1):113.
Abstract
The processes of energy/momentum exchange in rotating plasma flows placed into crossed magnetic and electric fields is an issue of importance. Such flows are capable of transforming the energy from different degrees of freedom into another. The resulting energy and momentum from one degree can be altered owing to the interaction of the coupled nonlinear radial, axial and azimuthal electron-ion oscillations. These processes may lead to the acceleration of flow in the axial direction with these stable effects. This technology can be instrumental for creating efficient thrusters employing pulse transformations manipulated by the electric and magnetic fields. This would be suitable for space propulsion and other environmental effects.
Keywords
Rotating plasma flow; Energy/momentum exchange; Intermodal exchange; Crossed magnetic field
Introduction
The problem to be analyzed
The behavior of rotating flows in crossed physical fields is of interest for different technical applications and natural phenomena. For example, in the Hall thrusters the orthogonal electric 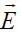 and magnetic
and magnetic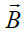 fields are used to produce thrust by altering the behavior of plasma [1-8]. As a result, the electrons can experience
fields are used to produce thrust by altering the behavior of plasma [1-8]. As a result, the electrons can experience 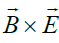 rotation or the Poynting vector in the azimuthal direction and shift ions to move only in the axial direction. Thus, a radial magnetic field confines rotating electrons which compensate the space charge of the flow, while an axial electric field alters by accelerating the motion of the electrons. The similar mechanisms may be related to the acceleration of the high-energy jets near black holes and pulsars where one should take into account the gravitational fields [9-11]. These examples show that any combination of electric, magnetic, non-inertial and gravitational fields may propel unusual processes of energy/momentum transfer. This allows us to speak about redistribution of energy/momentum between the macroscopic degrees of freedom of the macroscopic flows.
rotation or the Poynting vector in the azimuthal direction and shift ions to move only in the axial direction. Thus, a radial magnetic field confines rotating electrons which compensate the space charge of the flow, while an axial electric field alters by accelerating the motion of the electrons. The similar mechanisms may be related to the acceleration of the high-energy jets near black holes and pulsars where one should take into account the gravitational fields [9-11]. These examples show that any combination of electric, magnetic, non-inertial and gravitational fields may propel unusual processes of energy/momentum transfer. This allows us to speak about redistribution of energy/momentum between the macroscopic degrees of freedom of the macroscopic flows.
As an object of such a kind, the present paper takes a cylindrical plasma flow in an external magnetic field. Such rotating plasma flow is one of simple physical patterns, however, manifesting different nonlinear wave-like properties owing to the electron and ion fluids may be treated as a set of coupled nonlinear radial, axial and azimuthal oscillators of different kinds that define the variety of wave forms. On the other hand, there are a numerous technical applications including plasma Hall thrusters where such flows have been applied.
There are two principally different physical situations for the development of such nonlinear wave-like phenomena. First, one can expect the emergence of wave-type behavior when the initial state coincides with one of the equilibrium states. In this case, well-known weakly nonlinear waves may be observed [12-14]. However, for initial states not close to equilibria, such an approach is inadequate and one can try to investigate wave-like behavior near some time-dependent state [15-21]. Such states, in the form of highly nonlinear plasma oscillations and patterns, are little understood but have indeed were shown to exist [20-25]. Following these works, we will consider some features of energy/momentum transfer for such nonequilibrium plasma flows and discuss the applications of these effects for a accelerating propulsion facility or natural phenomena.
Asymmetric plasma flow in the crossed magnetic fields
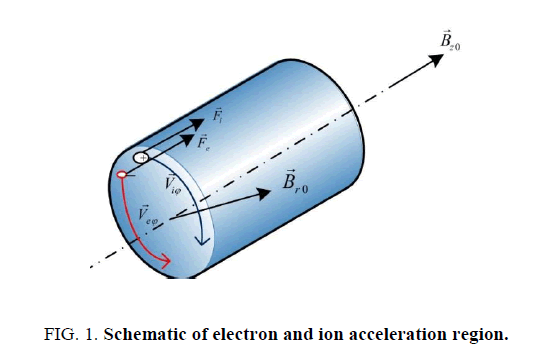
The proposed scheme of this plasma flow is presented in Figure. 1. In this experiment, one can make such a configuration of magnetic fields with the help of a solenoid ( Bz0 ) and permanent magnets ( Br0 ). The change of axial magnetic flux can induce an azimuthal electric field that rotates electrons and ions in different directions as seen in Figure. 1. Such a type of azimuthal acceleration is known as an induction acceleration widely used in accelerator technology. The azimuthal electron and ion flows interact with the radial component ( Br0 ) via the Lorentz force, this leads to the axial acceleration of electrons and ions in the axial direction. Owing to this process, the transformation of azimuthal momentum transfers into axial momentum. Despite the difference in the electron me and ion mi , masses the electron and ion fluids can move together due to the action of the inherent electric fields of the plasma.
To understand the behavior of the flow depicted in Figure. 1. we will study the following model with an azimuthally symmetric plasma where but will include the azimuthal components in the electric and magnetic fields. We will propose there is an additional external spatially homogeneous magnetic field which depends only on time.
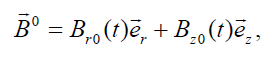
where Br0 (t) and Bz0 (t) are some known functions. Such an external magnetic field induces an electric field which can possibly rotate electrons and ions in different directions if the model is successful.
With the linearity of the Maxwell equations, we can present the total electric and magnetic fields of the system. Let us assume we have mean values with a perturbation such as:
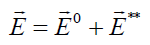
and
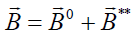 ,
,
Where the perturbed electric 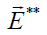 and magnetic
and magnetic 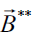 fields are defined by the dynamic processes in itself plasma medium described by the standard cold-fluid model in the dimensionless form.
fields are defined by the dynamic processes in itself plasma medium described by the standard cold-fluid model in the dimensionless form.
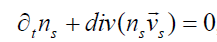 , (1)
, (1)
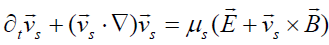 , (2)
, (2)
Here 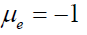 and
and 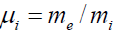 , where the label s = e relates to the electron fluid and the label s = i - to the ion fluid. The perturbed fields are defined by
, where the label s = e relates to the electron fluid and the label s = i - to the ion fluid. The perturbed fields are defined by
The perturbed fields are defined by
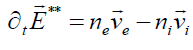 , (3)
, (3)
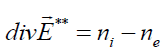 , (4)
, (4)
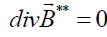 , (5)
, (5)
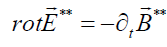 (6)
(6)
Where 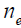 is the electron density,
is the electron density,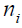 is the ion density,
is the ion density,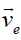 is the electron fluid velocity,
is the electron fluid velocity, 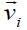 is the ion fluid velocity?
is the ion fluid velocity?
To write these equations in terms of dimensionless variables, let the initial electron density 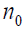 , the initial radius of plasma cylinder R0 , the inverse electron frequency
, the initial radius of plasma cylinder R0 , the inverse electron frequency 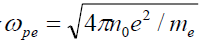 , where e is the electric charge, as the natural scale of all densities, coordinates and time.
, where e is the electric charge, as the natural scale of all densities, coordinates and time.
All velocities are normalized by the 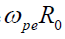 , the electric field normalized by the
, the electric field normalized by the  and the magnetic field is normalized by the
and the magnetic field is normalized by the 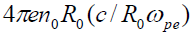 , where c is the speed of light.
, where c is the speed of light.
From equation of induction (6) written for external magnetic field 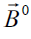 in integral form
in integral form
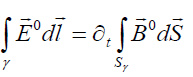
this follows that the external electric field has only an azimuthal component determined by
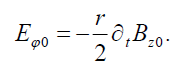 (7)
(7)
This relation suggests to seek the possible solution of the governing set in the form
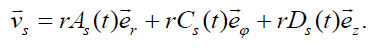 (8)
(8)
Also, supposing that the intrinsic electric field of the system is similar to the velocity field (8), we can write
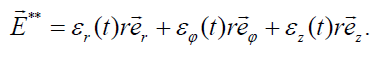 (9)
(9)
And set
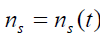 . (10)
. (10)
In this case, from (6) follows that
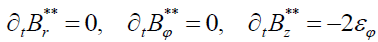 , (11)
, (11)
i.e. for the initial conditions 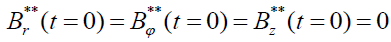 . Only the component
. Only the component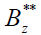 may be distinct from zero inside the plasma cylinder and the one is the function of time. It means that
may be distinct from zero inside the plasma cylinder and the one is the function of time. It means that 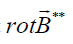 = 0. Moreover, substituting (9) and (10) into Eq. (5) we get the temporal relation between the electron and ion densities
= 0. Moreover, substituting (9) and (10) into Eq. (5) we get the temporal relation between the electron and ion densities
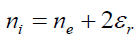 . (12)
. (12)
This relation assumes the current moves radially between the anode and the cathode of the thruster. By inserting (7)-(9) into (1)-(6) yields:
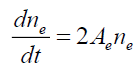 , (13)
, (13)
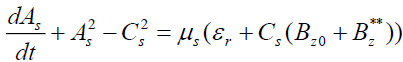 , (14)
, (14)
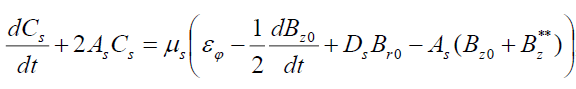 , (15)
, (15)
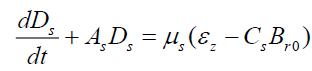 (16)
(16)
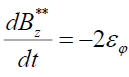 , (17)
, (17)
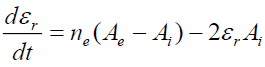 , (18)
, (18)
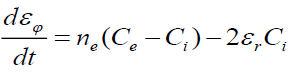 , (19)
, (19)
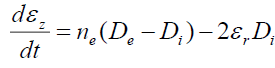 . (20)
. (20)
For completeness, note that in the case of (12), the continuum equation for ions automatically holds true for Eqs. (13) - (20). To show the acceleration effect, it is convenient to proceed from specific characteristics to total properties such as total momentum or total kinetic energy of electron and ion fluids for the whole plasma cylinder. To do this, the limits for electron and ion fluids form the plasma medium. Let us define the total number of particles of the s-kind as
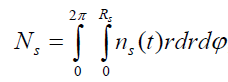 , (21)
, (21)
Where Re (t) is the limit for the electron fluid and Ri (t) i is the limit for the ion fluid? For spatial homogeneous densities ne(t) and ni (t) we have
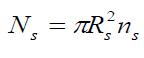 (22)
(22)
Which represents the law of particle conservation since there is no particle loss or particle-creation in the control volume 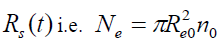 and
and 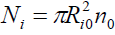
where 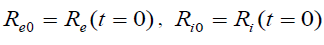 and
and 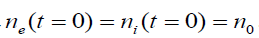 .
.
For simplicity, set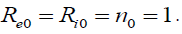 Then from (22) we get
Then from (22) we get
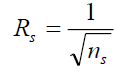 . (23)
. (23)
Calculate the total kinetic energy for electron and ion fluids as
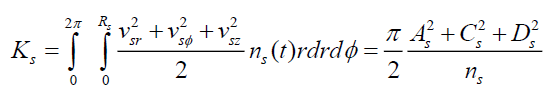 (24)
(24)
And the total axial momentum as
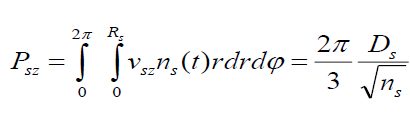 . (25)
. (25)
Equations (12) - (25) form the basis for most of the analysis to follow.
Basic properties of rotating flow
Now we consider the basic dynamical features of the profile (8) in cylindrical geometry. In this flow field, there appears an azimuthal component of the vorticity,
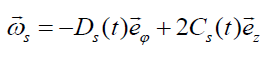 , (26)
, (26)
which confirms that besides the azimuthal flow rotation in the plane z = const, there is also rotation in the plane φ= const. Since the velocity and electric fields given by Eqs. (8) And (9), respectively have the same form, there is now also an azimuthal magnetic field component, which leads to additional 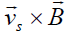 force components that can affect the flow dynamics. In order to demonstrate the influence of various factors on the acceleration of the flow one should rewrite Eq. (2) as
force components that can affect the flow dynamics. In order to demonstrate the influence of various factors on the acceleration of the flow one should rewrite Eq. (2) as
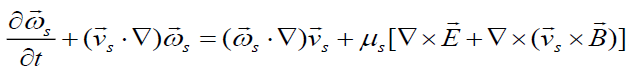 .
.
It is easy to see that 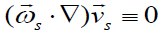 for (8) and (26). If the electrical field has purely a potential origin, then
for (8) and (26). If the electrical field has purely a potential origin, then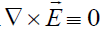 .
.
It implies that the value of vorticity 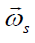 is defined only by the term
is defined only by the term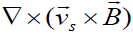 .
.
However, at the initial stage, the dynamics of the flow is always determined by the cylindrical geometry of the system when electrical and magnetic fields play a weak role. To clarify this peculiarity, it is useful to consider the behavior of the corresponding flow for cold neutral gas with density n and velocity 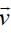 . Substitution of Eq. (8) into the corresponding continuity equation yields
. Substitution of Eq. (8) into the corresponding continuity equation yields
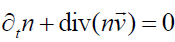 ,
,
And the force-free momentum equation
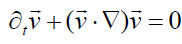 ,
,
Yields the following set
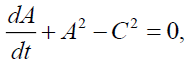 (27)
(27)
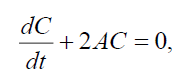 (28)
(28)
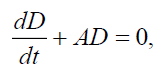 (29)
(29)
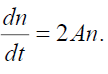 (30)
(30)
This set of ordinary differential equations determine the primitive, temporal solution for force-free flow which may be useful for understanding the physical features of the full set (13)-(20). In particular, the solutions of Eqs. (28)- (30) can be expressed via a function A(t) :
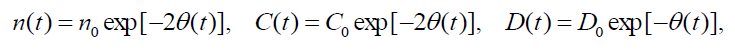 (31)
(31)
Where C0 and D0 are some integration constants, and value
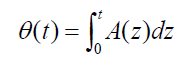 (32)
(32)
This underlines the temporal nonlocal character for dependencies corresponding to (8). It means that in real plasma flow, highly nonlinear oscillations of the radial velocities can occur without any noticeable change of the densities, azimuthal and axial velocities for the electron and ion fluids. This is because the temporal dependences of the values given by relations (31) depend only on time integrals of A(t) so that the oscillations in the latter are smoothed out. Such solutions do not exist in the linear limit since higher harmonics do not appear. As is seen from (31) and (32), here the radial and axial flow components are strongly coupled, especially for A(t) < 0, when there is flow compression in the radial direction. One can thus have axial acceleration in the asymmetric flow owing to energy transfer from the radial flow. On the other hand, for A(t) > 0 , the difference between the D(t) in the symmetric and asymmetric cases is insignificant, since D(t) decreases with time and there is no enhancement of axial flow.
It is instructive to consider the limit C0 = 0 when according to (31) there is no flow rotation 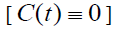 and Eq. (27) has the following solution:
and Eq. (27) has the following solution:
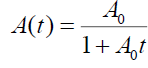 , (33)
, (33)
Here, A(t = 0) = A . If A0<0 , then Eq. (33) describes an approach to a singularity of flow. That is a well-known intrinsic feature of fluids especially in inviscid pressure less limit.
Now we consider the case of rotating flow when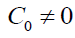 , then using the expression for C(t) from Eq. (31) we can rewrite (27) as
, then using the expression for C(t) from Eq. (31) we can rewrite (27) as
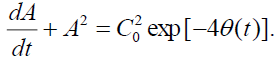 (34)
(34)
Differentiating Eq. (34) we get
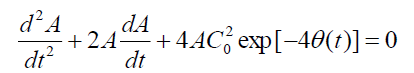
From which with the help of (34) we obtain
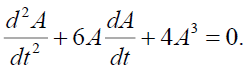 (35)
(35)
This nonlinear ODE can be integrated numerically. As an illustration, we present here three cases of rotating primitive flow when 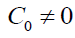 corresponds to a non-zero derivative
corresponds to a non-zero derivative 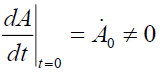 .
.
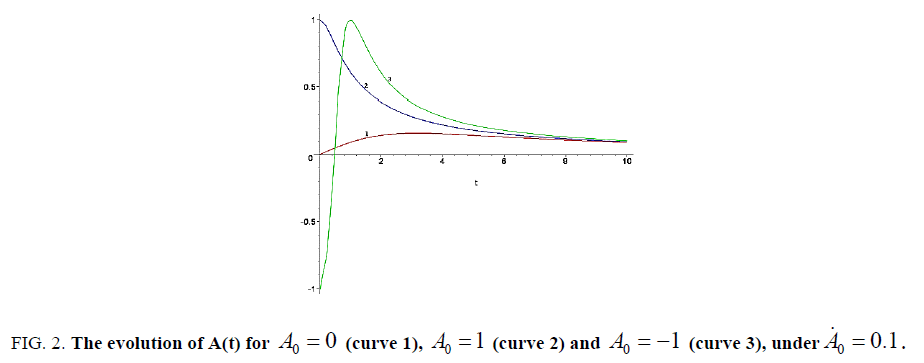
We ![]() = 0.1 put in all present computations sketched in Figure. 2. Here, curve 1 shows the evolution of a system for initially free from radial flow, curves 2 and 3 relate to an expanding and compressible flow. As is seen from these curves, the rotation eliminates the singularity and for large times ( t > 5) the evolution takes place in a similar way. We see that in all cases the radial flows remain relatively small. However, according to (31) and (32), this brings about a strong damping of n(t), C(t) and D(t) . That is, here a temporal nonlocal effect is involved. However, when the radial velocity is initially negative (curves 3), the corresponding rotational C(t) and axial D(t) components, as well as the density n(t) , decreases much slower than in other cases. Such behavior might be accounted for by the fact that in all cases the dynamics of the free-flow involves only inertial acceleration, resulting in radial expansion of the fluid.
= 0.1 put in all present computations sketched in Figure. 2. Here, curve 1 shows the evolution of a system for initially free from radial flow, curves 2 and 3 relate to an expanding and compressible flow. As is seen from these curves, the rotation eliminates the singularity and for large times ( t > 5) the evolution takes place in a similar way. We see that in all cases the radial flows remain relatively small. However, according to (31) and (32), this brings about a strong damping of n(t), C(t) and D(t) . That is, here a temporal nonlocal effect is involved. However, when the radial velocity is initially negative (curves 3), the corresponding rotational C(t) and axial D(t) components, as well as the density n(t) , decreases much slower than in other cases. Such behavior might be accounted for by the fact that in all cases the dynamics of the free-flow involves only inertial acceleration, resulting in radial expansion of the fluid.
Figure 2: The evolution of A(t) for A0= 0 (curve 1), A0= 1 (curve 2) and A0= -1(curve 3), under A0= 0.1. .
Dynamics of a rotating plasma flow
In this model, the acceleration effect is caused by the azimuthal electric field which comes about the variation of an external magnetic flux [Eq. (7)]. In our model, it is possible to go beyond the approach of quasi-neutrality [Eq. (12)]. These processes can lead to the generation of a local azimuthal time-dependent electric field [Eq. (12)], which may accelerate the rotation of the electron and ion fluids in different directions. As previously mentioned, the interactions of these flows with the external magnetic field propel the axial acceleration of the flow. In fact, here we get the process of redistribution of energy and momentum of flow in the external magnetic fields.
Thus, the objective is to find a parameter such as 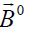 which makes the model successful. Such information may be drowned by solving a pure initial value problem for this rotating plasma flow describing the set (1)-(6). As an illustration of these possibilities, we present a few graphs corresponding to the simplest cases when the external magnetic field
which makes the model successful. Such information may be drowned by solving a pure initial value problem for this rotating plasma flow describing the set (1)-(6). As an illustration of these possibilities, we present a few graphs corresponding to the simplest cases when the external magnetic field 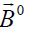 is the permanent, and there are no other initial electric fields in plasma flow:
is the permanent, and there are no other initial electric fields in plasma flow: 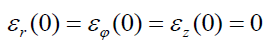 and
and 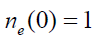 . In all computations, we shall use
. In all computations, we shall use 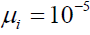 . To avoid singular behavior that may invalidate our starting equations (1)-(6). We shall restrict our numerical examples to an initially expanding and slowly rotating plasma passing along the z-axis by setting
. To avoid singular behavior that may invalidate our starting equations (1)-(6). We shall restrict our numerical examples to an initially expanding and slowly rotating plasma passing along the z-axis by setting 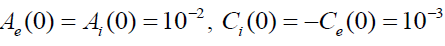 and
and
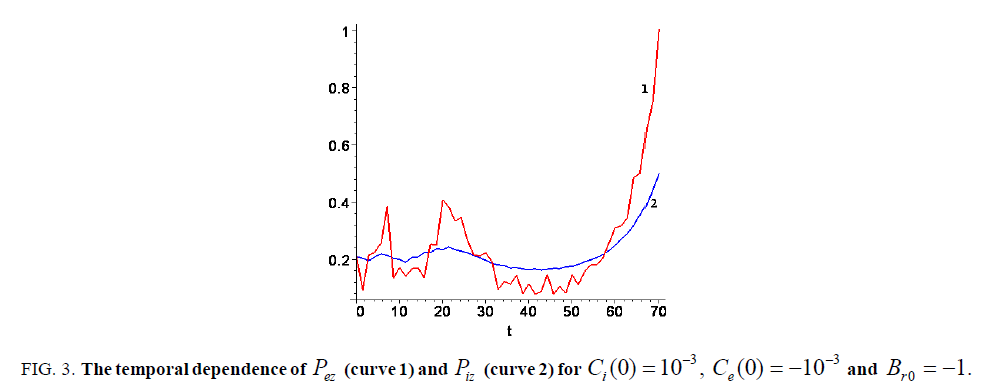
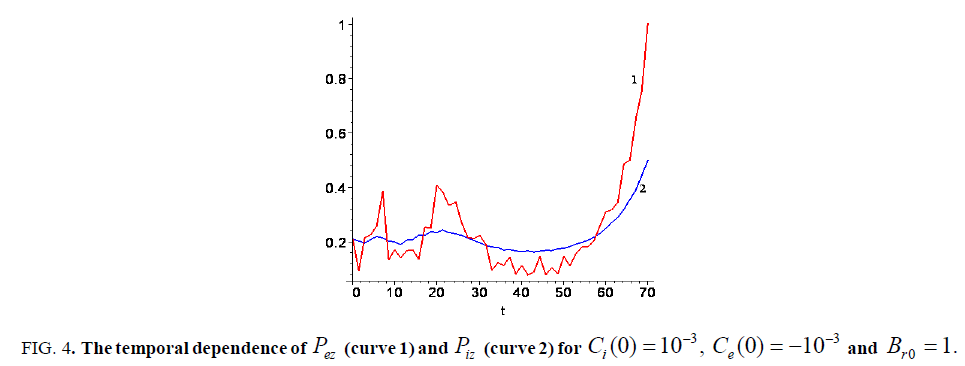
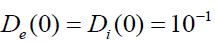 . In Figure. 3 the total axial momentum for electron
. In Figure. 3 the total axial momentum for electron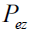 and ion
and ion 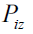 fluids are plotted when Bz0=1 and Br0= -1, and in Figure.4. the same dependencies are presented for the case when Bz0=1 and Br0= 1. Namely these dependences illustrate what typically occurs with the flow dynamics when the value Br0 changes with the opposite sign.
fluids are plotted when Bz0=1 and Br0= -1, and in Figure.4. the same dependencies are presented for the case when Bz0=1 and Br0= 1. Namely these dependences illustrate what typically occurs with the flow dynamics when the value Br0 changes with the opposite sign.
Figure 3: The temporal dependence of Pez (curve 1) and Piz (curve 2) for Ci(0)= 10-3 , Ce(0)= -10-3 and Bro= -1.
Figure 4: The temporal dependence of Pez (curve 1) and Piz (curve 2) for Ci(0)= 10-3 , Ce(0)= -10-3 and Bro= 1.
As seen from these graphs, in all both cases we observe an acceleration of electron and ion component that reflects the coupling of electron and ion fluids. The initial conditions induce a redistribution of momentum to the axial degree of freedom from other degrees of freedoms in the rotating plasma flow. Here we observe the strong growth of total axial momentum in the electron scale of time. In particular, it means that there is a week influence due to the collisional phenomena on the momentum transfer. This is if the character electron time is less than the corresponding characteristic collision time.
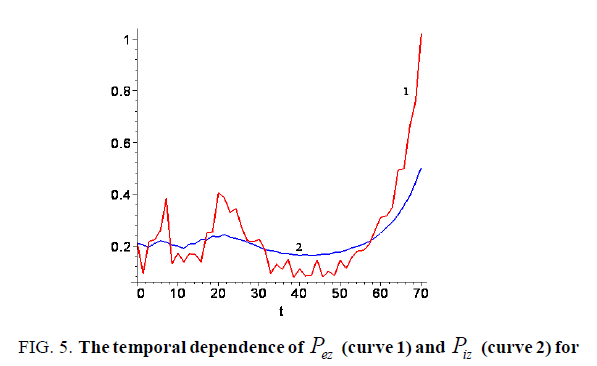
We now examine whether the above presented results remain valid if electron and ion fluids are initially rotated in the same direction. Figure.5. illustrates when we set 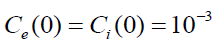 and all parameters coincide with the ones for Figure. 3. As is seen from the graphs of Figure. 3-5, maximum acceleration of ion fluid remains at the same level. Whereas the dependences of the electron component in Figure. 3 and 5 are quite different from similar one in Figure.4. Thus, we come to the conclusion about a weak influence of initial velocity distribution and a strong effect of the external magnetic field on the processes of energy/momentum exchange.
and all parameters coincide with the ones for Figure. 3. As is seen from the graphs of Figure. 3-5, maximum acceleration of ion fluid remains at the same level. Whereas the dependences of the electron component in Figure. 3 and 5 are quite different from similar one in Figure.4. Thus, we come to the conclusion about a weak influence of initial velocity distribution and a strong effect of the external magnetic field on the processes of energy/momentum exchange.
Figure 5: The temporal dependence of Pez (curve 1) and Piz (curve 2) for Ci(0)= 10-3 , Ce(0)= -10-3 and Bro= -1.
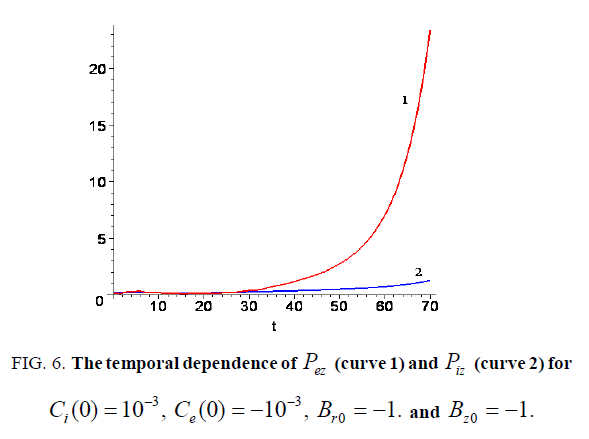
So, we take the initial state which is distinct from the state plotted in Figure. 3 only by Bz0= -1; the corresponding results are sketched in Figure. 6. Here we see that the behavior is quite different from the dependences in Figure. 3 and 4. Moreover, in this case one can observe the increase of the acceleration effect both electron and ion components.
Figure 6: The temporal dependence of Pez (curve 1) and Piz (curve 2) for Ci(0)= 10-3 , Ce(0)= -10-3 and Bro= -1. and Bzo = -1.
Summing up, all these results testify to the possibility of energy/momentum accumulation in the axial mode which is brought about by the energy/momentum transfer from other degrees of freedom due to the external magnetic fields. However, one can expect that such effects will be increased for external magnetic nonstationary fields [Eq. (6)].
From the comparison of Figure. 3 and 4, it follows that the change of sign for Br0 brings about the form of the observed dependences, the shape of the electron and ion dependences change over the course of time. It seems that these peculiarities are caused by not only asymmetrical rotation of electron and ion fluids for the same initial data. Such a behavior is made possible by the strong nonlinearity of the set (1)-(6). Thus, depending on the initial values, the system can evolve in many ways and this issue is required the further investigation.
Besides, the effect of intermodal exchange has been established in the hydrodynamic approach for a cold, neutral flow model of the cylindrical homogeneous plasma flow. Our study is based on using particular but exact nonlinear solutions of the electron and ion fluid equations. In fact, here we have the redistribution of energy/momentum between the macroscopic degrees of freedom in the cold plasma flow placed into the permanent magnetic fields. So we again would like to stress that we can significantly increase the acceleration effect by using non-stationary magnetic fields when the vortex component of the electric field has been produced.
Concluding thoughts
Results of this assessment implies that degrees of freedom of electrons and light ions in a plasma are capable of being changed based upon a weak magnetic field. The key is this capability is easily applicable to a Hall Thruster where the approach requires smaller chamber lengths to accelerate particles in the axial direction for thrust [4-8]. Results also provide limitations for the weak magnetic field which can be of a lower intensity than current systems. Such flows may be stable.
Other applications exist for other than space propulsion applications. Here, atmospheric disturbances such as tornadoes or even hurricanes may be altered by adjusting, assuming a large electromagnetic capability exists, to ameliorate weather conditions [26-28]. In the layers of the Earth's atmosphere contain a large number of charged particles under a vortex formation where the Earth’s magnetic, electric and non-inertial fields have dealt with gravity-heat and electrical processes of the Earth via the generation of geostrophic fluxes [26-31]. Thus, the present approach makes it possible to understand the processes of energy/momentum conversion in the atmosphere vortex entities of different scales [27-32].
Proceeding from the presented results for the dynamics of rotating plasma flows, we may also speculate about the similar effects for a gravitational field in the non-inertial reference systems. In a general case, we can represent the electric and magnetic fields in terms of a scalar 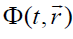 and vector
and vector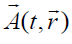 potentials as
potentials as
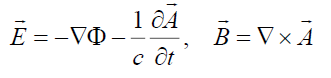
That allows us to write the Lorentz force for the charge q moving with velocity 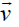 with respect to an immobile reference system in the form
with respect to an immobile reference system in the form
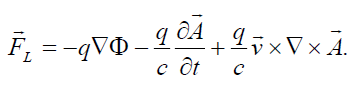 (37)
(37)
Now we consider the relation for gravitational force 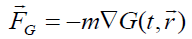 in a non-inertial system:
in a non-inertial system:
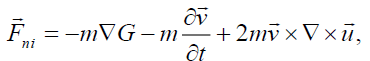 (38)
(38)
Where 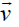 is the velocity of mass m with respect to moveable reference system rotating with
is the velocity of mass m with respect to moveable reference system rotating with 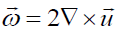 respect to the fixed frame. Here
respect to the fixed frame. Here 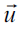 is the velocity of rotation for moveable frame. As is seen from Eqs. (37) and (38), these forces have the same structure if we put
is the velocity of rotation for moveable frame. As is seen from Eqs. (37) and (38), these forces have the same structure if we put 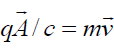 . This point suggests that the processes of energy/momentum exchange and acceleration in rotating frames may come about by a similar way to the considered processes in the rotating plasma flow. We may venture a guess that such mechanisms may be realized in different astrophysical phenomena where one should also take into account the strong gravitational fields. Thus, the manifestations of energy/momentum exchange in different natural phenomena may be quite diverse, but there are some general features that are yet to be observed in almost all of these systems.
. This point suggests that the processes of energy/momentum exchange and acceleration in rotating frames may come about by a similar way to the considered processes in the rotating plasma flow. We may venture a guess that such mechanisms may be realized in different astrophysical phenomena where one should also take into account the strong gravitational fields. Thus, the manifestations of energy/momentum exchange in different natural phenomena may be quite diverse, but there are some general features that are yet to be observed in almost all of these systems.
References
- Kim V.Main physical features and processes determining the performance of stationary plasma thrusters. J Propul Power. 1998;14:736-43.
- Goebel DM, Katz I. Fundamentals of Electric Propulsion: Ion and Hall Thrusters. Jet Propulsion Laboratory California Institute of Technology: JPL Space Science and Technology Series; 2008.
- Morozov AI, Savelyev VV. Fundamentals of stationary plasma thruster theory. In Reviews of plasma physics; 2000. 203-391p.
- Choueiri EY. “Plasma oscillations in Hall thrusters.” Phys Plasmas. 2001;8:1411-26.
- McDonald MS, Gallimore AD. “Rotating spoke instabilities in Hall thrusters.” IEEE Trans Plasma Sci. 2011;39:2952-53.
- Fisch NJ, Raitses Y, Fruchtman A. “Ion acceleration in supersonically rotating magnetized-electron plasma.” Plasma PhysControl Fusion. 2011;53:124038.
- Smirnov A, Raitses Y, Fisch NJ. “Controlling the plasma flow in the miniaturized cylindrical Hall thruster.” IEEE Trans Plasma Sci.2008;36:1998-2003.
- Ellison CL, Raitses Y, Fisch NJ.“Cross-field electron transport induced by a rotating spoke in a cylindrical Hall thruster.Phys Plasmas. 2012;19:013503.
- Bogovalov SV, Chechetkin VM, Koldoba AV et al. Interaction of pulsar winds with interstellar medium: numerical simulation. Mon Not R Astron Soc. 2005;358:705-15.
- Koldoba AV,Ustyugova GV, Romanova MM, et al. Simulations of jet formation from a magnetized accretion disk. Astrophys Space Sci. 1995;232:241-61.
- Aharonian FA, Bogovalov SV,Khangulyan D. Abrupt acceleration of a ‘cold’ ultrarelativistic wind from the Crab pulsar. Nature. 2012;482:507-09.
- Davidson RC. Methods in Nonlinear Plasma Theory. New York: Academic Press; 1972.
- Dodd RK,Eilbeck JC, Gibbon JD, et al. Solitons and Nonlinear Wave Equations. London: AcademicPress; 1982.
- Diamond PH, Itoh SI,ItohK. Physical Kinetics of Turbulent Plasmas. Modern Plasma Physics: Cambridge: Cambridge University Press; 2010.
- Sirovich L, “Turbulence and the Dynamics of Coherent Structures.” Q Appl Math.7987;45:561-71.
- Barenblatt GI. Scaling Phenomena in Fluid Mechanics. Cambridge University Press; 1994.
- Haller G,YuanG. Lagrangian Coherent Structures and Mixing in Two-Dimensional Turbulence.” Physica D. 2000;147:352-70.
- Kono M, Skoric MM. Nonlinear Physics of Plasmas. Berlin: Springer-Verlag; 2010.
- Karimov AR, Schamel H, Shcheglov VA. “Amplification of Initial Perturbations in Simple Hydrodynamic Systems.” Phys Lett A. 2000;272:193-96.
- Karimov AR. “Nonlinear waves in twirling plasmas.” J Plasma Phys.2009;75:817-28.
- Karimov AR, Sten?o L, Yu MY. “Coupled flows and oscillations in asymmetric rotating plasmas.” Phys Plasmas. 2009;16:102303.
- Karimov AR,Godin SM. “Coupled radial–azimuthal oscillations in twirling cylindrical plasmas.” PhysicaScripta. 2009;80:035503.
- Karimov AR, Yu MY,Stenflo L. Large quasineutral electron velocity oscillations in radial expansion of an ionizing plasma.” Phys Plasmas. 2012;19:092118.
- Karimov AR, Yu MY,Sten?o L. “Asymmetric oscillatory expansion of a cylindrical plasma.” J Plasma Phys. 2013;79:10071009.
- Karimov AR, Yu MY, Sten?oL. “Flow oscillations in radial expansion of an inhomogeneous plasma layer.” Phys Lett A. 2011;375:2629-36.
- Krasilnikov EY. “Electro magnetohydrodynamic nature of tropical cyclones, hurricanes and tornadoes.” J Geophys Res. 1997;102:571.
- Tinsley BA.“The global atmospheric electric circuit and its effects on cloud microphysics,” Rep Prog Phys. 2008;71:066801.
- Murad PA, Boardman MJ, Brandenburg JE. A?ecting Weather-Mitigating a Tornado Vienna: Morningstar. Appl Phys; 2012.
- Reiter R. Phenomena in Atmospheric and Environmental Electricity. Amsterdam: Elsevier; 1992.
- Artekha SN,Belyan AV. “On the role of electromagnetic phenomena in some atmospheric processes.” Nonlinear Proc Geoph. 2013;20:293-304.
- Marshall TC,Rust WD. Electrical structure and up-draft speeds in thunderstorms over the southern great plains.J Geophys Res. 1995;100:1001-15.
- Eyink GL, Sreenivasan KR. “Onsager and the theory of hydrodynamic turbulence,” Rev Mod Phys. 2006;78:87-135.