Research
, Volume: 13( 2)Why Transfinite Set-Theory is Wrong and an Alternative Theory of Numeric Structures
- *Correspondence:
- David Peralta
Department of Physics, Medical University of Silesia, Katowice, Poland
E-mail: davidperaltaval@gmail.com
Received: March 25, 2024, Manuscript No. TSPA-24-130726; Editor assigned: March 28, 2024, PreQC No. TSPA-24-130726 (PQ); Reviewed: April 12, 2024, QC No. TSPA-24-130726; Revised: March 03, 2025, Manuscript No. TSPA-24-130726 (R); Published: March 10, 2025, DOI. 10.37532/2320-6756.2025.13(2).402.
Citation: Peralta D. Why transfinite Set-Theory is wrong and an alternative theory of numeric structures. J Phys Astron. 2025;13(2).402.
Abstract
Set theory is a formalization of the existence and fundamental properties of mathematical objects as collections of elements and/or elements included in collections. Its formulation is so basic and comprehensive that it has been postulated as the foundation of all mathematics. Perhaps, the major achievement of set theory is that, after being criticized by many reputable mathematicians and philosophers since its appearance, it is now commonly accepted as the primary explanation of the most basic components of mathematics: Numbers; and not only the numbers we have needed or we may ever need but all the numbers that could potentially exist. In set theory, an infinite sequence of numbers exists not as the mere projection of a construction algorithm but as a complete and self-identical mathematical object: A set. In set theory the words infinite and infinity do not refer to the property of growing endlessly (potential infinity) but to a definite magnitude; a number; the actual infinity. As a result of such a conception, set theory arrives at the conclusion that there exist infinitely many infinities, each one with a different value. The set of postulates, proofs and theorems used to justify the existence of such infinities is commonly known as transfinite set-theory. The first part of this work shows how some of the properties and theorems applied to infinite sets, in set theory, necessarily lead to internal and fundamental contradictions under classical logic, even when the idea of actual infinity is accepted. Throughout the second part, motivated by the necessity of an alternative to transfinite set-theory, due to the incapacity of such a theory to explain some of the findings shown in the first part (especially the proof of the existence of as many rational as irrational numbers), the author develops a theory to provide a better understanding of infinite sequences of numbers.
Keywords
Set Theory, Infinity; Infinite sets; Georg cantor; Transfinite numbers; Real analysis; Number theory; Diagonal argument; Irrational numbers; Cardinality; Aleph null; Continuum hypothesis; Cantor's theorem; Bijection; Bijective; Objectivity; Countable-infinite sets; Uncountable sets
Introduction
Set theory is a formalization of the existence and fundamental properties of mathematical objects as collections of elements and/or elements included in collections. Its formulation is so basic and comprehensive that it has been postulated as the foundation of all mathematics. The invention of set theory is commonly attributed to George Cantor (1845-1918), a mathematician who was born in Saint Petersburg, Russian empire and acquired most of his academic formation in Germany, where he also developed most of his career. Perhaps, the major achievement of set theory is that, after being criticized by many reputable mathematicians and philosophers since its appearance, it is now commonly accepted as the primary explanation of the most basic components of mathematics: Numbers; and not only the numbers we have needed or we may ever need but all the numbers that could potentially exist. In set theory, an infinite sequence of numbers exists not as the mere projection of a construction algorithm but as a complete and self-identical mathematical object: A set.
Some fundamental properties of sets
Set theory postulates some properties that are inherent to all sets, including infinite sets. Two of the most important properties of sets are:
Cardinality: It is the property of possessing a determined number of elements. If A is a set whose elements are {x, y, z}, it is said that the cardinality of ? is 3 or:
|A|=3.
Power set: It is the property of implying the existence of a set of all the subsets contained in a set. If A is a set whose elements are {x, y, z}, then there exists a set P(A), called the power set of A, whose elements are:
{{φ;}, {x}, {y}, {z}, {x, y}, {x, z}, {y, z}, {x, y, z}} and it is said that its cardinality is 8 or |P(A)|=8.
Some fundamental theorems of Set-Theory
By the acceptance of the mentioned properties, two fundamental theorems are derived:
Cantor-Schroder-Bernstein Theorem: Which states that, if there exist injective functions f: A→B and g: B→A between the sets A and B, then there exists a bijective function h: A→B. In terms of the cardinality of the two sets, this classically implies that if |A| ≤|B| and |B| ≤ |A|, then |A| = |B|; that is, A and B are equipotent [1].
Cantor’s theorem: Which states that, for any set A, the set of all subsets of A, the power set of A, has a strictly greater cardinality than A itself [2].
Conception of infinity in set theory
The validity of the properties and theorems listed above is almost evident for any finite set but it is problematic when it is accepted for infinite sets as well. However, since infinite sets are seen as completed and self-identical entities in set-theory, there is nothing fundamentally different between them and finite sets. That is because in set theory the words infinite and infinity do not refer to the property of growing endlessly (potential infinity) but to a definite magnitude; a number; the actual infinity. As a result of such a conception, as it will be shown further on in this work, set theory arrives at the conclusion that there exist infinitely many infinities, each one with a different value. The set of postulates, proofs and theorems used to justify the existence of such infinities is commonly known as transfinite set-theory.
In the following section, I will show how the above properties and theorems applied to infinite sets necessarily lead to internal and fundamental contradictions under classical logic, even when the idea of actual infinity is accepted [3].
Cantor’s actual infinity
The main-stream conception of infinite sets today comes from the work of Georg Cantor. One of Cantor’s main objectives was to give a totalizing character to his Set Theory. To achieve that, he needed to state that every mathematical object could be conceived as a set and has, at least, the same basic properties shared by all sets; then, infinite sequences of numbers must be sets and they must have the properties of cardinality and power set, which will consequently lead to the existence of infinite different infinities. Cantor was a strong believer in the existence and consistency the actual infinity. Contrary to the most accepted notion of infinity in the history of mathematics and philosophy until the rise of set theory and still now for some, which is that infinity is not a number nor a quantity but just the property held by an entity of having no end, no limit, no term, no finish, also called potential infinity, Cantor defended the idea of actual infinities being complete, closed and definite mathematical objects and that every potential infinity exists only within the path of the actual infinity. Many prestigious mathematicians and philosophers of his time decidedly disagreed with many of Cantor´s proofs, methods and ideas. However, his thoughts found great acceptance within Christian theologists, especially in neo-Thomist circles and were promoted by Pope Leo XIII himself. The religious appeal of Cantor’s ideas is not surprising [4]. Cantor must have been aware of the importance of them from a theological perspective. God is infinite but he is also absolutely complete; nothing exists beyond him; thus, God cannot be potentially infinite; God cannot be conceived as something capable of growing because that would mean that he is imperfect. God must be an actual infinity from him and within him, all other infinities were created, not suggested or projected or launched, but formed as complete, self-identical infinities; many kinds among them but none with the property of growing endlessly because, in that unthinkable case, they could potentially extend themselves beyond God. Actual infinities have a lot of sense in theology but not in mathematics [5]. The concept of actual infinity produces not only logic and mathematic contradictions, but a type of contradiction that is even deeper and more evident: A semantic contradiction. In most dictionaries, the word infinite has the meaning, both as a noun and as an adjective, of limitless, endless, extending beyond any finite extension or quantity, etc.; from the Latin infinitus (limitless, borderless, endless). On the other hand, Cantor’s concept of actual infinity seems to be just an esoteric, thus confusing, version of the concept of finite. Ludwig Wittgenstein (1889-1951), known as one of the most influential philosophers of the Twentieth century, whose work was mainly focused on logic, the philosophy of mathematics and the philosophy of language, was a firm critic of Cantor’s misuse of the words infinite and infinity and its catastrophic consequences for the foundations of mathematics [6]. It is difficult to establish whether religious beliefs were the deepest motivation for Cantor’s work or just a refuge from the rejection of his ideas by the mathematics community of his time. However, religious beliefs may have been an important motivation for some of his followers of the upcoming generation of mathematicians, such as A. A. Fraenkel, whose intellectual interests included finding logical explanations for some fantastic events described in the Torah. However, Cantor’s ideas may have never found enough support among the mathematics community without the applause of David Hilbert (1862-1943), who became the most influential mathematician of his generation and whose religion had nothing to do with the Judeo Christian God but, maybe, with his deep belief in the completeness and total coherence of mathematical systems, from which not even the infinite could escape. Hilbert endorsed Cantor’s Set Theory and that support was enough to turn Cantor’s misleading ideas into mathematical dogma until today. More interesting than establishing Cantor’s, Hilbert’s and Fraenkel’s motivations and biases, it would be trying to understand why the vast majority of the mathematics community has been defending, for more than a century, the concept of actual infinity or even ignoring that from that concept were derived, ideas such completed infinite sets, the cardinality of infinite sets, power sets of infinite sets, transfinite numbers, etc. However, it would not be the first time in history that humanity fell into such a kind of collective self-deception [7].
I will argue against some of the proofs presented by Cantor, which have contributed to the general misconception about infinite sequences of numbers, especially, to the wrong general belief that the concepts of cardinality and power set can be applied to them the same way they are applied to finite sets [8].
Logical development and faults of transfinite set-theory
The following is the logical process for the construction of transfinite set-theory. I will present the main premises and methods used by Cantor in the construction of his theory and some irrefutable proofs of its faultiness [9].
Cardinality of the set of natural numbers
The first postulate for the development of Transfinite Set-Theory is that there exists a set ? whose elements are all the natural numbers and its cardinality is infinity (∞). Further findings forced Cantor to distinguish this infinity from other infinities; for that reason, he eventually named it N0 (aleph null) or countable infinity since natural numbers are the numbers used for counting. N0 is the least infinite cardinal number. Note that this implies that the infinite sequence of natural numbers is a self-identical entity; a completed set with a definite number of elements encompassing all possible natural numbers [10].
Self-contradictory statement about the cardinality of natural numbers: The cardinality of the set of natural numbers ?, which is also the set of all finite cardinal numbers, is the infinite cardinal N0, for which, given any arbitrarily large natural number (n), the following is always true:
n< N0
That implies that different from what happens to any of its subsets, the set of all finite cardinal numbers has a cardinality that is greater than its greatest element. By definition, if there is a greatest element in a set, the set should be finite. If there is not a greatest element, the cardinality should be undetermined or undeterminable.
Here we start seeing how infinite sets are excluded from at least one of the most necessary aspects of cardinality, with no other justification than the determination of attributing that property to all sets.
Once the first postulate is accepted, we can ask ourselves whether other infinite sets, such as the set of even natural numbers or the set of integers, have cardinality N0 as well; whether they have the same number of elements as the set ?.
Bijectivity implies equipotency
Since every natural number can be transformed into a singular even natural number by the function ?(?)=2? and every even natural number can be transformed into a singular natural number by the function ?(?)=?/2, then, from the Cantor-Schröder-Bernstein Theorem we can affirm that there exists a bijection between those two sets. And, since we accept that infinite sets have a definite number of elements, we can also affirm that a bijective relation between two of them implies their equipotency; which means, they have the same number of elements. There exist just as many natural numbers as even natural numbers. It results evident that the same would happen with any infinite subset of the set of natural numbers and also with any finite multiplication of such sets, as the set of integers or the set of even integers. All those sets are called countable-infinite sets and their cardinal is N0.
And, what about the rational numbers?
Cantor’s diagonal snake
In 1890, Cantor published a proof of the accountability of rational numbers by using what is known today as Cantor’s diagonal snake or Cantor’s first diagonal. This proof starts by assuming that, as it happens with finite sets, all sets that can be mapped (disposed in a one-to-one display) to any countable-infinite set have a bijection with it and, thus, with the set of natural numbers. To prove that integers and rational numbers can be mapped to each other, Cantor organized all positive fractions in a squared array, in which each row contains all fractions with the same numerator and each column contains all fractions with the same denominator. Then, all fractions can be listed starting from the top-left corner and moving right down covering all the fractions in each diagonal and ignoring the ones that can be simplified, as follows:
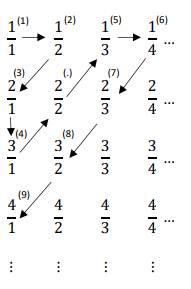
We get the following mapping:
1, 2, 3, 4, 5, 6, 7, 8, 9, &nS;
1, 1/2, 2, 3, 1/3, 1/4, 2/3, 3/2, 4, &nS;
Then, we just have to add 0 at the beginning of the list and, after each fraction, its negative, as follows:
1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11,12, 13, &nS;
0,1, -1,1/2, -1/2, 2, -2, 3, -3, 1/3, ¼, -1/4,&nS;..
Therefore, the set of rational numbers has a bijective relation with the set of integers and, by extension, with the set of natural numbers; which means, it is countable- infinite; thus, the cardinality of the set of rational numbers is N0.
Inconsistency of Cantor’s diagonal snake
The problem with the proof above is that it implies that, differently from what happens with finite sets, there are right and wrong methods for mapping infinite sets, depending on the result we want to obtain. If we apply that same principle to the rest of mathematics, they would become inconsistent.
We may decide to map natural and rational numbers by listing rational numbers in order of their denominators, for example; as follows:
1, 2, 3, 4, 5, 6, &nS;
1/1, ½, 1/3, 1/4, 1/5, 1/6,&nS;..
By using this method, we would never be able to map any fraction with a numerator different from one because denominators of one will always be equal to their pair and will increase infinitely as the counting terms increase. Cantor assumes that the above is not a problem in this case because, according to him, we only need one method that makes the mapping possible to affirm that a given set has the same size as the set of natural numbers. We also could claim the opposite; that we only need one method that makes the mapping impossible to affirm that a given set has a different size from the one of natural numbers. The choice of one assumption instead of the other is arbitrary unless a logical explanation invalidates the second method for infinite sets, other than the necessity of proving a specific hypothesis.
In any other field of exact sciences, we would say that, if two different methods drive to different conclusions, there may be a mistake in the formulation of the hypothesis or at least one of the methods is wrong; and the reason to choose one method instead of the other is normally not because it is the one that proves our hypothesis. Think for example in the case of a neolithic physicist who wants to prove that things exposed to direct light get hotter. He shows his audience how a bowl of water gets hotter when it is exposed to direct sunlight and when it is placed close to a fire. But when someone asks him to try the same under the moonlight, the physicist refuses to do so, saying that it is needed just one method that can turn the water hotter in the presence of light to prove that light makes things hotter. In the case of Cantor mapping the rational numbers to the integers, as well as in the case of the neolithic physicist, there is no reason to prefer one of the methods better than the other, other than the necessity of proving a specific hypothesis. Both methods work the same for finite sets; thus, an explanation of why both do not work for infinite sets is required unless we consider ourselves as neolithic mathematicians. I am going to take Cantor’s arbitrary assumption as valid, just because it will further help me to refute another proof made by him.
Contradictory statements about the cardinality of rational numbers
Set theory tells us that the cardinality of a set is always greater than or equal to the cardinality of any of its subsets. By the function f(x)=1/x, we know that there exist at least as many rational numbers within the interval (0,1) as numbers in the set of all natural numbers. Thus, the cardinality of the set of rational numbers within the interval (0,1) must be N0. By the definition of rational numbers, we know that they can only have a finite number of decimal digits (n) in their decimal representation. We also know that the total number of rational numbers cannot be higher than the total number of possible permutations of the natural numbers between 0 and 9 in (n) positions. We also know that such a number is equal to 10?, which is a finite number because (n) is finite. Thus, the total number of rational numbers within the interval (0,1) is finite; therefore, the cardinality of such a set is lesser than N0, which contradicts the first underlined statement.
When counterintuitive just means wrong
Sometimes, counterintuitive conclusions are the result of unknown or unexpected complexities existing in reality. That is the case of some paradoxical outcomes from quantum mechanics and general relativity. Counterintuitive has become a very appealing word since the discoveries of Plank, Bohr, Einstein, Hubble, Heisenberg and Schrödinger, turning out to be, perhaps, one of the most expected signs of scientific breakthroughs. That, however, could have turned itself into a misleading intuition, growing deep roots into the field of mathematics, where conclusions are normally not derived from experimental observations, as they are in physics, but from rigorous logical demonstrations which are supposed to dissipate all wrong intuitions in the process. That, although, is not what happens in Set-Theory. Sometimes, counterintuitive conclusions are just the result of false assumptions or wrong methods. That is the case of the famous Hilbert’s Hotel allegory, which has been one of the symbols of transfinite set-theory for a century and shows how it is possible to accommodate an infinite number of new guests in an already fully occupied hotel with infinite rooms.
Let us analyze the following reasoning about the cardinality of countable infinite sets:
- The cardinality of a set is a measure of the number of elements of the set
- The set of integers has countable-infinity elements
- The set of rational numbers has countable-infinite elements from a, b and c, it follows
- Integers and rational numbers have the same cardinality. They have the same number of elements
If we can presume that countable-infinity (N0) represents the number of elements of a set (magnitude of quantity), we may also presume the existence of a number representing an infinitely short magnitude (N-1). Then, if we accept that the reasoning above, regarding the cardinality of countable infinite sets, is true, we must accept that the following is true as well:
- The distance between places A and B is the sum of the distances between all consecutive places between A and B
- The distance between Amsterdam and Berlin can be divided into an infinite number of infinitely short consecutive distances
- The distance between Amsterdam and Chongqing can be divided into an infinite number of infinitely short consecutive distances from a, b and c it follows:
- The distance between Amsterdam and Berlin is equal to the distance between Amsterdam and Chongqing.
That is what happens when we use the concepts infinite, infinitely or infinity not as the property of having no end but as a magnitude of distance or quantity. After accepting that the sets of natural numbers, even natural numbers, integers and rational numbers have all the same number of elements, then we can ask ourselves what would be the cardinality of the set of real numbers.
Equipotency between the set of real numbers and the set of real numbers within the interval (0,1)
Any number within the interval (0,1) can be transformed into a positive real number by the function f(x)=x/1−x and any positive real number can be transformed into a number within the interval (0,1) by its inverse f(x)−1 which is f(y)=y/1+y means, there is a bijective relation between those two sets of numbers; therefore, they have the same number of elements; they are equipotent. But, is their cardinality N0?
Cantor’s diagonal argument
In 1891 Georg Cantor published a proof of the uncountability of the set of real numbers using what is called the diagonal argument or Cantor’s second diagonal. It starts by assuming that the set of real numbers is countable-infinite and, thus, it has the same cardinality as the set of natural numbers. Then, we construct an enumerated hypothetical list of all the real numbers within the interval (0,1) in its binary representation (no strict order is necessary). Once we have the list, we construct a number, named diagonal number, by selecting, from each number in the list, the value of the decimal position that corresponds to the position of the number in the enumeration, as follows:
1 → 0.00101011;
2 → 0.11100010;
3 → 0.10000111;
4 → 0.10101010;
5 → 0.01010101;
Diagonal number=0.01000;
After that, we create a new number, named the anti-diagonal number, by changing all the values of the decimal string.
Antidiagonal number=0.10111&nS;
The new number is a real number within the interval (0,1) but it is not in the enumerated list; therefore, there exist more real numbers than natural numbers.
The above could seem absurd but it is not; at least, it is not absurd at the most superficial level. We may say that the diagonal number cannot be constructed because the list would grow exponentially as the string of decimal digits grows linearly, thus, the diagonal would never encompass more than a small fraction of the list. But remember that we are accepting that N0, the countable infinity, is a self-identical definite value and that is exactly the quantity of natural numbers that have ever existed, exist and will ever exist. The number of decimal digits is N0 and the size of the list is also N0, they cannot be smaller or larger than N0. Thus, we have a squared array and both the diagonal and antidiagonal numbers can be constructed, resulting in a number that it is not in the list and leading to the conclusion that the cardinal of the set of real numbers, also known as the cardinal of the continuum (c), is greater than the cardinal of the set of natural numbers: c>N0.
It is important to mention that the diagonal argument cannot be applied to the set of rational numbers because they do not have an infinite number of decimal digits. Their decimal digits are finite and any finite number is always lesser than N0; we do not know how lesser but, in any case, lesser than N0. Therefore, we cannot have a squared array and the diagonal number cannot be constructed.
Proof A: There exist as many rational as irrational numbers
I will present an arithmetic proof demonstrating that there exists one and only one irrational number per each existing rational number and vice versa; which implies that the cardinality of those two sets is exactly the same: |Q|=|R−Q|. That, by extension, demonstrates that the cardinality of the set of real numbers is N0, which contradicts the conclusion derived from Cantor’s diagonal argument.
Statement about rational numbers
Every rational number can be expressed as a finite simple continued fraction:
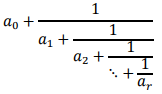
Where (a0) is an integer, (ai) is a positive integer for i=1, 2, &nS; , r and (ar) ≠ 1.
Statement about irrational numbers
Every irrational number can be expressed as an infinite simple continued fraction:
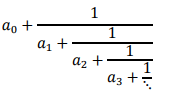
Where (a0) is an integer and (ai) is a positive integer for i = 1, 2, &nS;
Existence of irrational numbers
For every pair of rational numbers (p, q), there exists at least one irrational number (u), such that (u) is between (p) and (q). This can be confirmed by observing the last nested fraction of the simple continued fraction representation of two similar rational numbers.
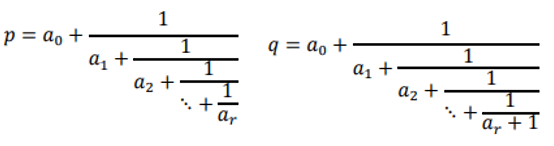
There exists at least one irrational number (u) between (p) and (q):
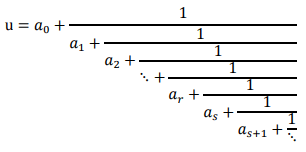
Where (α0) is an integer and (ai) is a positive integer for i = 1, 2,&nS; , r, s, (s + 1), &nS; and (ar) ≠ 1.
Existence of rational numbers
For every pair of irrational numbers (u, v), there exists at least one rational number (q), such that (q) is between (u) and (v). This can be confirmed by observing the last nested fractions that two similar irrational numbers have in common in their simple continued fraction representation; more exactly, at the nested fraction where they start to diverge from each other.
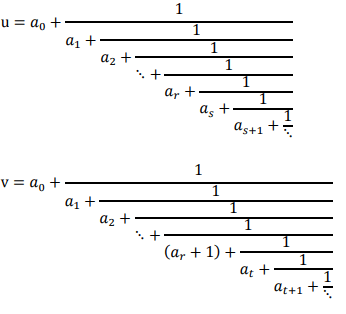
There exists at least one rational number (q) between (u) and (v).
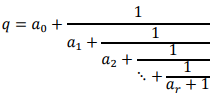
Where (a0) is an integer and (ai) is a positive integer for i=1, 2, &nS;, r, s, (s+1)&nS; , t, (t+1), &nS; and (ar) ≠ 1.
If (u) and (v) share the same nested fractions indefinitely, we can say (u) and (v) are mathematically indistinguishable from each other, thus: u=v.
Final statement of proof A
As it is true that (u) is between (p) and (q) for every (p, q) ∈ Q and (u) ∈ (R−Q) and it is also true that (q) is between (u) and (v) for every (u, v) ∈ (R−Q) and (q) ∈ Q, we can say that there exists one and only one irrational number per each existing rational number and vice versa.
Therefore, |Q|=|R−Q|. Q.E.D.
Since the set of real numbers is the union of the sets of rational and irrational numbers and the cardinality of the union of two countable-infinite sets must be countable infinite as well, then, the cardinality of the set of real numbers must be N0, which contradicts the conclusion derived from Cantor’s diagonal argument.
Once we accept that the cardinality of the set of real numbers (c) is higher than N0, we should inquire whether there exist other infinite cardinal numbers different from N0 and ?.
Cantor’s theorem
Cantor’s Theorem affirms that any set (including infinite sets) is strictly smaller than its power set. In order to prove that theorem, Gerhard Hessenberg (1874-1925) used a method which is not exactly the same but very similar to Cantor’s diagonal argument. That is why it is sometimes called the diagonal set. The proof is presented below:
Theorem: Let f be a map from set A to its power set P(A). Then F:A → P(A) is not surjective. As a consequence, card(A) < card (P(A)) holds for any set ?.
Proof: Consider the set B={X ∈ A | x ∈ f(x)}. Suppose to the contrary that f is surjective. Then there exists E ∈ X such that f(e)=B. But by construction, E ∈B⇔E∈ F(E)=B. This is a contradiction. Thus, ? cannot be surjective. On the other hand, g:A → P(A) defined by A {F} is an injective map. Consequently, we must have card(C)
Disproof of cantor’s theorem by using cantor’s methods
We can also prove, by using Cantor’s diagonal snake, that the power set of the set of natural numbers is countable-infinite; meaning that those two sets are exactly the same size or, in other words, they have the same cardinality.
Cantor’s diagonal snake method tells us that any set whose elements can be arrange in a squared array is countable, the same way the set of rational numbers is countable. We know that the number of possible subsets in any set A is 2 to the power of the number of elements in A. We know, according to Cantor, that the number of elements in the set of natural numbers is N0, so we can say that card (P(A))=2N0 = 2 × 2 × 2 &nS; Thus, we can arrange all elements X ∈ P(A) in a squared array as follows:
X1 X2
Then multiplying by two:
x1 x2
??3 ??4
Then multiplying by two:
Then multiplying by two:
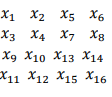
We can make an array of the same characteristics than the one Cantor used to prove the countability of the set of rational numbers and then use the same mapping method to prove that any infinite set has the same cardinality as its power set. There is no reason to say that this method is acceptable in the case of rational numbers but unacceptable in the case of power sets, other than the need to prove some hypothesis and disprove others, which is arbitrary and thus, illogical.
Contradictory statements about the cardinality of the set of natural numbers and its power set
Set theory tells us that the cardinality of the set of natural numbers is N0 and the cardinality of its power set is 2N0=N1. Now, let us ask ourselves up to how many digits is a natural number allowed to have in its binary representation. If our answer is an infinitely large finite number, then, that number, regardless how large it is, is a finite number (n). Thus, the quantity of all possible natural numbers could not be greater than the number of permutations of 0 and 1 in (n) positions, which is 2?; a finite number; therefore, we would have to state that the cardinality of the set of natural numbers is a finite number and the cardinality of its power set is also a finite number, which contradicts the first underlined statement. If, on the other hand, natural numbers could have an infinite number of digits (N0), then, the number of elements in the set of natural numbers would be given by 2N0=N1 and the cardinality of its power set would be 2N1=N2, which also contradicts the first underlined statement. Neither having a finite nor an infinite number of digits, natural numbers can satisfy what set theory states about them.
Cardinality does not apply to infinite sequences of numbers the same way it does to finite sets
It is been shown that some of the proofs published by Cantor have contradictory premises and/or arbitrary methodologic principles; and, as a result, contradictory conclusions can be derived when those methods are extended to other cases. It is possible to prove both, the countability and uncountability of the same infinite set, by using Cantor´s methods. The reason for such an inconsistency is that Cantor had to force his methodology in order to prove that the concept of cardinality applies to infinite sequences of numbers the same way it does to finite sets.
Cardinality, by definition, cannot be determined for infinite sequences of numbers. The idea of the existence of infinitely many infinities, each one with a different value, is derived from the wrong assumption that cardinality can be dete rmined for infinite sequences of numbers as it is for finite sets; therefore, the idea of multiple infinities was wrongly conceived. One of the consequences of such a mistaken conception or perhaps its actual origin, is the idea of the set of real numbers as a continuum and its topologic equivalence to the real line. And the foundation of such an idea may rest in the ancient misconception of lines as infinite collections of points. But, how could a sequence of non-dimensional objects form a one-dimensional one? How is that the sum of an infinite quantity of no lengths comes to be an infinite length? The notion of the sequence of real numbers as a continuum, as an object of constant, progressive and smooth change, as a numeric arrangement with no possible gaps, almost makes necessary the acceptance of the actual infinity and its meaning as the total quantity of real numbers and the erroneous belief on that infinite sequences of numbers have cardinality.
That does not mean that we cannot get an idea of the shape, potential and size of an infinite sequence of numbers, but the concept of cardinality is useless to achieve that. Saying that a sequence has an infinite number of elements is meaningless if we want to have a deeper understanding of it. The concepts of countability and uncountability of a sequence of numbers are meaningless too. Sequences of numbers are collections of numbers. Numbers are discrete objects. We can count an infinite number of discrete objects by using just natural numbers. By definition, all sequences of numbers are countable. On the other hand, the existence of a bijective relation between two infinite sequences of numbers cannot be taken as an equivalent of those sequences being of the same size. The special nature of infinite sequences of numbers allows them to have bijective relations with other infinite sequences of different sizes, like in the case of integers and even integers. Saying that those two sequences of numbers have the same size, just because they both are infinite and there is a bijective relation between them, is a useless oversimplification of their singular nature. In order to have a more accurate and useful idea of the shape, potential and size of numeric structures, we need to see sequences of numbers in a different way.
Moreover, proof A demonstrates that there exist or potentially can exist, as many rational as irrational numbers. That not only proves transfinite set theory wrong but also shows us how little we know about the real nature of numbers. An alternative theory is needed to understand what numbers are, how they come to exist, how they are different from each other and how many of them exist or potentially can exist.
Fundamentals of the theory of numeric structures
The development of the following theory was motivated by the necessity of an alternative to transfinite set theory, due to the incapacity of such a theory to explain the existence of one and only one irrational number per each existing rational number and vice versa, as it was shown in Section 3.5.1. (Proof A) of this work. The theory presented below is not exhaustive and it is not intended for a full comprehension of mathematics or to replace set theory but only to provide a better understanding of infinite sequences of numbers.
Semantic clarification
The following glossary clarifies the meaning of some words used in this and further sections:
Infinite: (adjective) limitless or endless in space, extent or size; impossible to measure or calculate.
Infinitely: (adverb) to an infinite extent or amount; without limit.
Indefinitely: (adverb) to an unlimited or unspecified degree or extent.
Infinity: (noun) the direction to which the value line extends itself infinitely.
Exist: (verb) when referring to the expression of a value in the value line, that such an expression can be constructed.
Justification
Every mathematic activity (operation, analysis, etc.) takes place in a specific mathematical context which uses a specific language to express mathematical values. Such a language is given by numeric structures.
Core definitions
The following definitions are the basis for the development of the theory of numeric structures:
Value line: There exists a continuum (object of constant, progressive and smooth change) of mathematical value called value line.
Number: There exists a specific value corresponding to a single point on the value line, which can be represented by an utter expression (an expression containing a finite quantity of symbols representing a finite quantity of mathematical objects). Such a value and its utter expression are indistinctly called a number.
Numeric structure: There exists a mathematical expression that represents a rule or a collection of rules for constructing a sequence of numbers. Such a mathematical expression and the sequence of numbers it constructs are indistinctly called a numeric structure.
Notation and some basic concepts
Numeric structures could be treated, in some situations, as sets of numbers. However, I will not use the set theory notation and terminology in this work for two reasons:
Numeric structures are languages for expressing mathematical values in a specific mathematical context, not just ordinary sets of numbers.
Infinite sets are commonly conceived as completed collections, while infinite numeric structures are non-completable; they are always under construction since the sequences of numbers they construct are infinite. An infinite numeric structure would never be smaller or greater than what we need it to be.
The difference between numeric structures and ordinary sets of numbers will become clearer as we advance through this work. The following notation is proposed in order to emphasize the above and also for its feasibility.
The generic expression nS{Λ} will be used to refer to numeric structures, where (Λ) describes the rules to create a sequence of numbers. The symbols used to denote such rules usually represent infinite sequences of numbers; thus, the expressions included in (Λ) have no algebraic meaning. Numeric structures can include arithmetic, geometric and/or other kind of mathematic relations as rules to construct sequences of numbers.
Basic numeric structures
Integers nS{Z}, non-negative Integers nS{|Z|} and positive integers nS{N} are the basic numeric structures. The rules to construct these sequences of numbers will not be described in this work.
Non-basic numeric structures
All other numeric structures are the description of the mathematic relation between the sequence of numbers they construct and the basic numeric structures. Rational numbers are an example of an arithmetic numeric structure represented as nS{Z/10}, meaning it is a numeric structure that constructs a sequence of all numbers which are the result of the division of any integer by any positive integer. Another example of a numeric structure based on an arithmetic relation is nS {± n√|Z|}, which constructs a sequence of all numbers that are the nth root of a non-negative integer. An example of a geometric-arithmetic numeric structure is the sequence of numbers commonly used to express angle values in radians: nS {+Z/A}.
A numeric structure does not determine the forms of representation of the sequence of numbers it constructs. That is determined by the numeral system. For example, the decimal and binary numeral systems are just two different representations of nS{N/10|Z|}.
The extension of a numeric structure can be limited to a certain interval. For example, the numeric structure commonly used to express Boolean values is nS {|Z| ≤ 1}; or, if we want to limit the value of angles to their decimal form between 0° and 360°, we will use {|Z| ≤ 360}; or if we need a numeric structure to express only sexagesimal values between (-1) and (1), we will ?? {-1 ≤ ?/60|Z| ≤ 1}; or to express the time elapsed within a day in terms of fractions of day but limited to the precision of a second, we can use Z {|N| ≤ N/N≤86400}, which is the sequence of all numbers resulting from the division of a non-negative integer by a positive integer in which the numerator is less than or equal to the denominator and the denominator is less than or equal to (86400).
Single expressions and groups of expressions in (Λ) can be restricted not only to certain intervals but also to other kinds of specific mathematical conditions. For example, if we are working in a mathematical context in which only prime numbers are needed or allowed, the language to express mathematical value in such a context can be described as nS {Na| (Na mod (Nb ≠ ∧ (1, Na))) ≠ 0}, which is the sequence of all positive integers such that the remainder of the division of such numbers by any positive integer, except one and themselves, is not equal to zero.
Union and intersection of numeric structures
Two or more numeric structures, nS{Χ}, nS{Ψ}, nS{Ω}, &nS;, can be merged to form a compound numeric structure nS {Λ}=nS {Χ} U nS {Ψ} U nS {Ω} ?&nS; = nS {U (Χ, Ψ, Ω &nS;)}.
For example, nS {Z/ N} can be merged with nS {±n√|Z|} to form: nS {? (Z/N, ±n√|Z|)}.
Similarly, we can construct a sequence of the numbers that two or more different numeric structures have in common. For example, the numeric structure for constructing the sequence of numbers that nS{2N} and nS{3N} have in common will be expressed as nS{∩ (2N, 3N)}.
Real numbers
We will use the expression nS{R} to represent the compound numeric structure whose components are all the infinitely many possible numeric structures of real value.
Note: Imaginary and complex numeric structures will not be discussed in this work.
Uniform infinitely intensive numeric structures nS{λ}
Some numeric structures can construct an infinite quantity of numbers between any two numbers constructed by them; we will call them uniform infinitely intensive numeric structures and we will use lower-case Greek letters in their generic expression; e.g., nS{λ}, nS{μ}, etc. A deeper explanation about the different types and classification of numeric structures will be provided in section 11.
Embedded and unembedded values in nS{λ}
A number is the utter expression of a specific mathematical value. Some values represented by numbers in a given uniform infinite intensive numeric structure, nS{λ}, may not have an utter expression in a different numeric structure, nS{??}. In such a case, we will say that the value of x(?) is embeddednS{λ} in ??{?} and unembeddednS{λ}?}. Nevertheless, we may find a non-utter expression of (?) in terms of ??{?}. A non-utter expression is any expression that contains an infinite number of symbols or a symbol representing an infinite number of mathematical objects.
For example, a number for the value of (φ) can be constructed by nS {Z/N}, in which it has the utter expression (x). That same value is unembedded in nS {Z/10|Z|} but it can be represented in it with the non-utter expression 3.14159 , where is a symbol representing an infinite number of non-repeating decimal digits. The same happens in relation to nS {Z}, in which (π) can be represented by the non-utter expression:
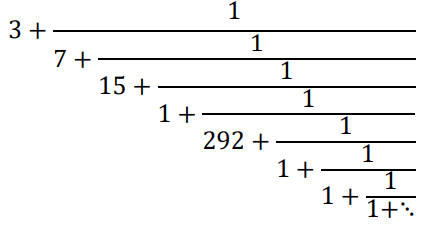
Where (...) represents an infinite number of nested fractions.12
On the other hand, in numeric structures like nS {Z/N}, integers can only be represented by non-utter expressions (containing an infinite number of symbols or symbols representing an infinite number of mathematical objects).
We may think that (π), (φ) and (e) are arbitrary symbols to abbreviate non-utter expressions, but they are not. They are arbitrary symbols to abbreviate utter expressions.
π=c/d where (c) is the perimeter of a circle and (d) is its diameter
φ=a/b such that a/b=a+b/a and (a>b>0)
e= lim (1+1/n)n
n→∞
which is an utter expression because infinity in this case refers to a direction in the value line, not to an infinite number of mathematical objects. Note that, unlike what happens with numeric structures, in set theory it does not make much sense to talk about expressing elements of one set in the language of another set. Let us see the case of nS{N√N}. The numbers constructed in such a structure using the first 15 positive integers would seem on the real value-line as follows (the reason to use the expression “real value-line” instead of “number line” or “real line” will be explained in section 10):

We may get the impression that the more non-negative integers are used to construct the sequence of numbers in this numeric structure the less likely is the existence of unembedded values in it; but, actually, no matter how many non- negative integers are used in the construction of this sequence, most values embedded in some other numeric structures will always be unembedded in this numeric structure. For instance, most values embedded in nS{|Z|π/N}, nS{|Z|π/N} and nS {|Z|/10|N|}, like 3/4, 1/2 and 1.124 will always be unembedded in nS{N√N}, regardless the number of positive integers used to construct its sequence of numbers. Now, let us check a different situation. See how, using the same partial construction, nS {|Z|/N} looks like on the real value-line, just to have a visual representation of this numeric structure:

Something similar happens in this case. Most values embedded in nS{Z√N} and nS {|Z|N/N}, like 2√2, 3√7, π and 3/5 will always be unembedded in nS {|Z|/N}, regardless the number of integers used to construct its sequence of numbers. While the embedded values in nS {|Z|/N} are commonly called non-negative rational numbers, the unembedded values in this numeric structure are known as non-negative irrational numbers.
A third example is given to enable a complete understanding of what numeric structures are. Let´s see how nS {|Z|/10|N|} looks like on a value line constructed the same way it was done for the previous two cases.

As in the previous case, most values embedded in nS{N√N} and nS {|Z|N}, like 2√2, 3/5 and will always be unembedded in nS {|Z|/10|Z|}, regardless the number of integers used to construct its sequence of numbers. However, they can be represented in ?? {|Z|10|Z|} with the non-utter expressions 1.4142, 3.1415 and 0.6283 &nS;, respectively. The same happens to some of the values embedded in nS {|Z|/N}, like 1/3, 9/11 and 1/7, which can be represented in nS {|Z|10|N|} with the non-utter expressions 0. 3, 0.81 and 0. 142847, respectively; where (d) represents an infinite repetition of the decimal digits (d). Here, it may be necessary to emphasize that non-utter expressions are not numbers; they do not express specific values; they are just approximations. That is true regardless how well we know the infinite mathematical objects of the expression because it never reaches a specific value. For that reason, we have that the following propositions are true:
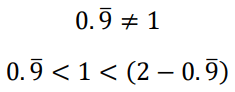
Note 1: Some numeric structures can construct numbers represented by more complex mathematical expressions.
For example: nS {Z + sin Z/} constructs a number with the utter expression 9+sin 15/π3.
Note 2: The embedded values in a compound numeric structure are the embedded values in all of its components. However, we cannot affirm the same about its unembedded values because an unembedded value in one of the components could be embedded in other.
It is clear now that the possibility of representing a value with an utter expression depends only on the numeric structure with which we decide to work.
Now, a question arises: Are there more embedded or unembedded values in any given nS{λ}?
Proof B: There are as many unembedded as embedded values in the decimal numeric structure {Z/10|N|}14
I already presented, in Section 3.5.1. (Proof A), a demonstration of the existence of one and only one irrational number per each existing rational number and vice versa; which is equivalent to state that there are as many unembedded as embedded values in ??{?/?}.
Now I will present an arithmetic proof demonstrating that there exists one and only one unembedded value in nS {Z10|Z|} per each embedded value in it and vice versa.
Statement about embedded values in nS {Z/10|N|}
Every embedded value in nS {Z/10|Z|} can be expressed as a finite decimal expression:
z. 3.1.2
Where (z) is the integer part, (nS) are decimal digits for ? = 1, 2, 1 and 1 ≠ 0.
Statement about unembedded values in
Every unembedded value in nS {Z/10|N} can be expressed as an infinite decimal expression:
Where (z) is the integer part and (di) are decimal digits for i=1, 2,.....
Existence of unembedded values in nS {Z/10|Z|}
For every pair of embedded values (p, q) in nS {Z/10 |N|}, such that p
q = z. ?1?2 &nS; ??
There exists at least one unembedded value (u) between (p) and (q):
u=z. d1d2..... (dr-1) dsds+1
Where (z) is the integer part of a number, (di) are decimal digits for i=1, 2, , r, s, (s + 1), &nS; and dr ≠ 0.
Existence of embedded values in nS {Z/10|Z|}
For every pair of unembedded values (u, v) in nS {Z/10|Z}, such that u
Equation
There exists at least one embedded value (q) between (u) and (v):
Equation
Where (z) is the integer part of a number, (di) are decimal digits for i=1, 2 , r, s, (s + 1) , t, (t + 1) and dr ≠ 0.
If (u) and (v) share the same decimal digits indefinitely, we can say (u) and (v) are mathematically indistinguishable from each other, thus: u=v.
Final statement of proof B
As p As p<u<q is true for every (p, q) embedded and (u) unembedded in ???? {?/10|Z|} and u<q<v is also true for every (u, v) unembdded and (q) embedded in ???? {?/10|Z|}, we can say that there exists one and only one unembedded value in ???? {?10|Z|} per each existing embedded value in it and vice versa. Q.E.D.
Theorem of parity: In any given nS{λ} there exists at least one unembedded value between any two embedded values and there exists at least one unembedded value between any two embedded values; thus, in any given nS{λ} there exists one and only one unembedded value per each existing embedded value and vice versa.
Now I will present a geometric proof demonstrating that there are as many unembedded as embedded values in any nS{λ}; that means, there is an embedded-unembedded value parity in every nS{λ}.
Wrapping representations and succeeding convergent
Any finite initial portion of a non-utter expression of the value (x) unembedded in nS{λ} represents a convergent of (x), which means it is an embedded value in nS{λ} approaching (x). For example: {3, 3.1, 3.14, 3.141, 3.1415, &nS;} are finite initial portions of 3.14159&nS;, which means they all are convergents of (?) from its decimal representation in nS {?10|Z|}. They are shown in the following value line:

Note that these convergents approach (π) only from one side of the value line. However, we can also construct non-utter representations of any value (x) unembedded in any nS{λ}, in which the convergents approach (x) from both sides of the value line, as it is the case of alternating series of progressively smaller values.
In order to represent π in nS {Z10|N|}, we can construct the alternating series:
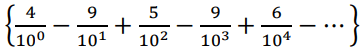
The first few convergents of (π) from this alternating series representation in nS {Z10|Z|} are: {4, 3.1, 3.15, 3.141, 3.1416 }.
When the convergents of a non-utter representation of the value (x) unembedded in nS{λ} approach to it from both sides of the value line, we will say that it is a wrapping representation of (x) and its convergents are wrapping convergents.
The first few wrapping convergents of (π) from its simple continued fraction representation in nS{Z/N} are shown below in computing order:
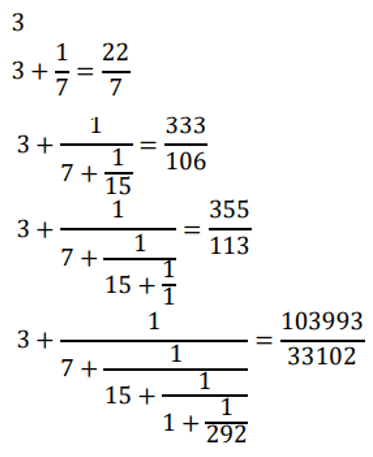
A pair of convergents that are computed one immediately after the other in a given wrapping representation will be called succeeding convergents. In the case shown above, the pairs (3, 22/7), (22/7, 333/106), (333/106, 355/113) and (355/113, 103993/33102) are succeeding convergents of (π). They are shown in the following value line:
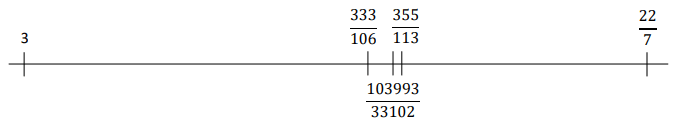
Note that the value of (π) is always between any pair of succeeding convergents of its simple continued fraction representation and, as the computation moves forward, succeeding convergents get closer to each other. In fact, we can affirm that a value (x) unembedded in any nS{λ} is between every pair of succeeding convergents of its wrapping representation and succeeding convergents of every wrapping representation get closer to each other as more of them are computed.
Geometric considerations
In order to avoid contradictory notions about value lines, we need to consider the following:
A point is a geometric object of 0 dimensions, which means, it has no length, width or thickness; thus, a succession of points cannot produce any object of dimensions greater than 0. A length of 0 plus a length of 0 equals a length of 0. However, points can be placed on objects of dimensions greater than 0 (e.g., a line).
A line is a geometric object of 1 dimension, which means, it has length but it has no width or thickness; thus, a succession of parallel lines cannot produce any object of dimensions greater than 1. A width of 0 plus a width of 0 equals a width of 0.
However, lines can be placed on objects of dimensions greater than 1 (e.g., a plane). It is impossible to fill the length of a line with objects that have no length (points).
A line segment is a line with well-defined ends marked with points. Between any two points on a single line there exists at least one-line segment and between any two segments of the same line there exists at least one point.
An infinitely short line segment is the best possible approximation to a point in terms of one-dimensional objects. The endpoints of such a segment will be called infinitely close points. The magnitude of Infinitely short line segments is undeterminable.
Geometric meaning of embedded and unembedded values
If {c1, c2, c3, c4, c5&nS;} are wrapping convergents of the unembedded value (x) in nS{λ}, we know that (x) is within the value-line segments {s1, s2, s3, s4, &nS;} formed by every pair of succeeding convergents, with increasing precision after each (si), as (i) increases towards infinity. That is shown in the following value line:
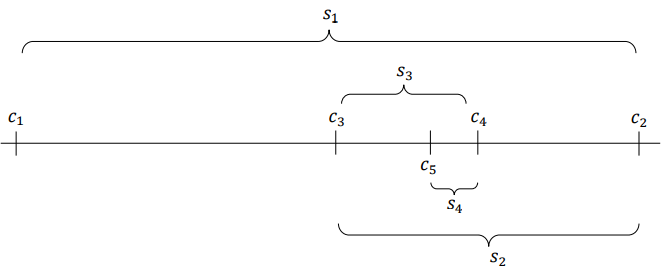
Note that (si) gets shorter as (i) increases but it will never turn into a single point because the value line is infinitely divisible; thus, the wrapping expression of an unembedded value (x) in nS{λ} can geometrically be defined as the representation of an infinitely short value-line segment, whose endpoints are its infinitely close succeeding convergents. Since it is true that every value (x) unembedded in any ??nS{λ} can be represented by a wrapping expression in terms of nS{λ}, which convergents are values embedded in nS{λ}, we can state that every unembedded value in any given nS{λ} corresponds to an infinitely short segment of the value line (in which nS{λ} has its domain)15, whose endpoints correspond to embedded values in nS{λ}.
Final statement of proof C
Since the above is true and it is also true that any value of the value line (where a numeric structure nS{λ} has its domain) has to be, by definition, either an embedded or an unembedded value in nS {λ} and it is also true that there exists at least one line segment between any two points on a line and there exists at least one point between any two segments of the same line, then, we can affirm that, in any given nS{λ}, there exists at least one unembedded value between any two embedded values and there exists at least one unembedded value between any two embedded values; thus, in any given nS{λ} there exists one and only one unembedded value per each existing embedded value and vice versa; that means, there is an embedded- unembedded value parity in every nS{λ}. Q.E.D. The Theorem of parity applies to infinitely intensive compound numeric structures as well since the geometric meaning of their embedded and unembedded values is the same as for infinitely intensive non-compound numeric structures. Therefore, at any portion of any nS{λ}, for all embedded numbers (a, b, c), where (a) is infinitely close to (b) and (b) is infinitely close to (c), we will find the following arrangement:

Where (ab) and (bc) are unembedded values in nS{λ}.
Alternative definition of irrational numbers
The above allow us to define irrational numbers (it would be better to call them irrational values) as the infinitely short line segments of the nS {?/N} value line (open interval) between the points that represent all rational numbers.
Unembedded values in numeric structures different from nS{λ}
We can also decide to accept unembedded values in other numeric structures different from uniform infinitely intensive numeric structures. For example, the numeric structure commonly used to express Boolean values, nS {|?| ≤ 1}, constructs only the numbers (0) and (1), to which we assign values of truth; (false) and (true), respectively. The proposition “this proposition is false”, though, cannot be qualified with any embedded value in nS {|?| ≤ 1}. Instead, when we compute it (validate any two options and correct if necessary), we will note that its value jumps infinitely from (0) to (1) and from (1) to (0). The value of truth of such a proposition is unembedded in nS {|?| ≤ 1}. We can say that such a value is undecidable or, actually, express it as the alternating series (1-1+1-1+ ?) or as the Boolean open interval (0,1). The same numeric structure can be used to qualify different fundamental states in quantum physics. Self-references, superpositions and irrational numbers may have in common that they can only be definite or valid under a specific structure of thought.
Parity paradox
Proof C also demonstrates that, in any given nD{λ}, there exists an infinite number of unembedded values between any two embedded values and vice versa. We may think that this contradicts the Theorem of parity, but it does not. When it is said of an object that it is infinite, it means that such an object is non-completable; thus, it is indefinite; it cannot be said that such an object is self-identical and, therefore, classical logic has to be applied to it with that consideration in mind.
Let us observe a particular case of the parity paradox. Consider the numeric structures nS {?/ ?}(positive rational numbers) and nS{?√?} (we will call them positive radical numbers). We have that, in each one of them, there are as many embedded values (positive rational and radical numbers respectively) as unembedded values (positive irrational and irradical values) and that some values are embedded in both of them (positive integers). A question arises: What is it there just after every positive integer? It cannot be a rational number because all integers are also rational numbers and, according to the Theorem of parity, there must be an irrational value between any two of them. It cannot be a radical number because all integers are also radical numbers and, according to the Theorem of parity, there must be an irradical value between them. Apparently, we have come to a paradox.
The right answer to that question is: it depends on the numeric structure with which we are working. If we are working with nS {?/?}, there is at least one irrational value between an integer and any other rational number. If we are working with nS{?√?} there is at least one irradical value between an integer and any other radical number. However, there is a third option. Just at the moment we started to join two different numeric structures in our mind, we have created a new numeric structure: nS {U (?/?, ?√?)}. In this numeric structure there is an infinite quantity of rational numbers between any two radical numbers; there is, as well, an infinite quantity of radical numbers between any two rational numbers; and, also, there exists at least one irrational-and-irradical value between any pair of rational, radical or rational radical numbers (integers). That means, just after every integer, in nS {U (?/ ?, ±?√?)}, there must be an irrational and irradical value. It is important to be aware of the numeric structure in which we are working to avoid confusion and paradoxes. Nevertheless, another question may arise: What is it there, just after every integer and its following irrational-and-irradical value? That will depend on what exactly is the integer to which we are referring and the stage of the construction of the numeric structure. For example, in nS {U (?/?, ?√?)}, using just the combinations of the first 15 positive and negative integers to construct its sequence of numbers, a radical number (2√10) will be just after the integer 3 and its following unembedded number; but, in that same stage of the construction, a rational number (13/3) will be just after the integer 4 and its following unembedded number. That situation, however, most likely would be different in a further stage of construction. For example, using the combinations of the first 30 positive and negative integers, a radical number (3√28) will be just after the integer 3 and its following unembedded number and another radical number (2√17) will be just after the integer 4 and its following unembedded number. Then, how would it be when the numeric structure is complete? As it is being emphasized since the beginning, infinite numeric structures are non-completable; they are always under construction since the sequences of numbers they construct are infinite. An infinite numeric structure would never be smaller or greater than what we need it to be. That is one of the properties that make them different from ordinary sets of numbers.
The real value-line and unspecifiable values
Let nS{?} be a compound numeric structure whose components are all the infinitely many possible numeric structures of real value. Therefore, the embedded values in nS{?} are all the infinitely many possible numbers in the real value-line (the real numbers). The Theorem of parity tells us that, even in this numeric structure, there exist as many unembedded as embedded numbers and, since all the numbers constructed by any possible numeric structure are already embedded in nS{?}, then the unembedded values in it cannot have any correspondent utter expression in any possible numeric structure. For that reason, the unembedded values in nS{?} will be called unspecifiable values. That means that there exist as many real numbers as unspecifiable values in the real value-line. Real numbers are a discrete sequence of numbers; they are not a continuum (this can be derived from the definitions of "value line" and "number" in section 5.3. and the definitions of "point" and "line" in section 7.2.). The real value-line, not the real numbers, is the continuum of real mathematical value. The real value-line is not a succession of numbers, as a line cannot be a succession of points. In order to avoid any confusion between the real numbers and the continuum of values where they exist, I have preferred to use the term “real value-line” instead of “number line” or “real line”. The reasoning above is also applicable to the imaginary numbers nS{?i} and the imaginary value-line.
Shape, potential and size of numeric structures
It is possible to have a more precise idea about the form of a numeric structure than the one provided by the concept of “cardinality”. In order to achieve that, we need to define the concepts of shape, potential and size in the realm of numeric structures.
Shape of nS{∧}
Every numeric structure has an intrinsic shape consisting in a series of properties which are identifiable and invariant along its construction process. The properties that determine the shape of a numeric structure are the following:
Shape of nS{∧} according to the value line in which it has its domain
Depending on the value line in which numeric structures have their domain, they can be classified as:
Real: If their domain exists only within the real value-line
Imaginary: If their domain exists only within the imaginary value-line
Complex: If their domain exists within both real and imaginary value-lines
Shape of nS{∧} according to the direction in which its construction advances
Depending on the direction in which numeric structures move after each stage of their construction proses, they can be classified as:
Positive: If they advance only towards infinity
Negative: If they advance only towards negative infinity
Reversal: If they advance towards zero
Positive-negative: If they advance towards both the infinity and negative infinity
Shape of nS{∧} according to their uniformity
Depending on the quantity of numbers they can construct on any value-line segment of the same length, numeric structures can be classified as:
Uniform: If they can potentially construct the same quantity of numbers on any value-line segment of the same length; e.g., nS {?/?}, n{-|?|}, nS{π ?}, etc.
Non-uniform: If they cannot construct the same quantity of numbers on any value line-segment of the same length; e.g., nS{?√2}, nS {15 ≤ ? ≤ 15/ ?≤15}, nS{??}, nS {??| (?amod (?? ≠? (1, ??))) ≠ 0}, etc.
Shape of nS{∧} according to their projection to infinity
Depending on the way numeric structures project themselves infinitely, they can be classified as:
Finite: If they do not project themselves infinitely in any sense; e.g., nS {? ≤ 10}, nS {-1 ≤ ? ≤ 1}, nS {|?|≤? ?≤86400}, etc.
Infinitely extensive: If they project themselves infinitely only towards any direction of the value line; e.g., nS{?}, nS{|?|}, nS{−?}, nS{2?}, nS{−2|?|+1}, nS {?/3}, nS {±(2?)}, etc.
Infinitely intensive: If they project themselves infinitely only deep inside the value line; e.g., nS {2? (|?| ≤ ?/)/?}, nS {|?|10|?| ≤ 360}, nS {sin |?|10|?|}, nS {−1 ≤ ?/? ≤ 1}, etc.
Infinitely extensive-intensive: If they project themselves infinitely both in direction of the value line and deep inside it; e.g., nS {?/?}, nS{±?√|?|}, nS {? (sin |?|/10|?|)}, etc.
Potential of nS{∧}
We will define the potential of a numeric structure as its capacity for constructing an infinite quantity of numbers. Depending on the scope towards numbers are constructed, we can establish the following hierarchy of criteria, in order to rank the potential of numeric structures:
- Capacity for constructing an infinite quantity of numbers both extensively and intensively
- Capacity for constructing an infinite quantity of numbers uniformly
- Capacity for constructing an infinite quantity of numbers in both positive and negative sides of the value line
- Capacity for constructing an infinite quantity of numbers
We can stratify the potential of real and imaginary numeric structures from the lowest to the highest according to the criteria above, as follows:
- Finite
- (Positive or negative or reversal) and (non-uniform) and (infinitely extensive or infinitely intensive)
- (Positive-negative) and (non-uniform) and (infinitely extensive or infinitely intensive)
- (Positive or negative or reversal) and (uniform) and (infinitely extensive or infinitely intensive)
- (Positive-negative) and (uniform) and (infinitely extensive or infinitely intensive)
- (Positive or negative or reversal) and (non-uniform) and (infinitely extensive- intensive)
- (Positive-negative) and (non-uniform) and (infinitely extensive-intensive)
- (Positive or negative or reversal) and (uniform) and (infinitely extensive- intensive)
- (Positive-negative) and (uniform) and (infinitely extensive-intensive)
The potential of a numeric structure is not an indicator of its size.
Size of nS{∧}
We will define the size of a numeric structure as the quantity of numbers it can construct. We can obtain three different size measurements of numeric structures depending of their shape:
Total size: It is the total quantity of numbers constructed by a numeric structure. Applies only to finite numeric structures.
Relative size: It is the quantity of numbers constructed by a numeric structure relative to nS{?}, whose relative size is (1). Applies only to uniform infinitely extensive numeric structures.
Partial size: It is the quantity of numbers constructed by a numeric structure within a specific interval at a specific stage of construction. Applies to all numeric structures.
While establishing the total size of any finite numeric structure is possible by just counting the quantity of numbers (embedded values) in it, the same task results impossible for any infinite numeric structure; and limiting ourselves to say that their size is infinite is not only useless but also very unprecise. Instead, we can obtain meaningful information about the size of infinite numeric structures by two different methods, depending on their shape.
Size of infinitely extensive numeric structures
We can measure the size of infinitely extensive numeric structures by calculating their density (D) in relation to the basic numeric structures within a specific interval. We can calculate the density of a numeric structure within the interval (a, b) as follows:
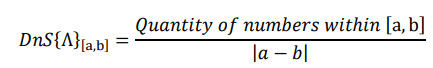
In order to compare the density of two or more non-uniform infinitely extensive numeric structures, the chosen interval has to be the same in all cases. As the density of non-uniform numeric structures can vary from one interval to another, the calculation of density will give us their partial size (only for the chosen interval). In the case of uniform infinitely extensive numeric structures, we just need an interval large enough to include a few of its numbers in order to obtain its relative size. Once we have calculated its density, we multiply it by the relative size of the basic numeric structure with which it shares its domain. The resulting value will be its relative size. We will establish the relative size of nS{|?|} and nS{?} as 1/2. For instance, we have that even integers, nS{2?} and odd integers, nS {±(2?−1)}, both have density (1/2) and, as they share their domain with the integers, nS{?}, their relative size is also (1/2). As another example, we have that nS{3|?|} and nS{3?-1} both have density (1/3) and, as one shares its domain with nS{|?|} and the other with nS{?}, their relative size is (1/6). The difference made by the construction of the number (0) in nS{3|?|} is negligible when comparing infinite numeric structures.
Size of infinitely intensive and extensive-intensive numeric structures
It is impossible to calculate the density of infinitely intensive and infinitely extensive-intensive numeric structures since they can construct an infinite quantity of numbers in a given interval. However, we can obtain meaningful information about the way in which a numeric structure grows by measuring its partial size; that is, within a specific interval at a specific stage of its construction process.
Standard construction process
We will establish the following as the standard process for the construction of any numeric structure ??{Λ}:
Starting with (0) and moving forward one unit at a time, we will take each non-negative integer and, subsequently, its opposite negative integer to make all possible combinations of them in (Λ) with themselves and with all other integers previously combined in (Λ).
The following would be the standard construction process for nS {?/?}:
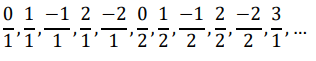
Stage of construction
For any non-negative integer (x), we will say that nS{Λ} is on the stage (x) of its construction when the last number of the sequence constructed under the ongoing standard construction process is the last possible combination of (x)’s opposite negative, if applies, (otherwise, (x) itself) with itself and all other integers already used in the construction process.
For instance, we say that nS {?/?} is on stage (0) when the standard construction process has produced only (0/1) or on stage (1) when the process has just finished with the construction of (1/1, -1/1) or on stage (2) when it has just completed the numbers produced by the following combinations (0/2, 1/2, -1/2, 2/2, -2/2).
Measurement of the partial size of nS{∧}
Once we have decided the finite interval (a, b) and the construction stage for which we want to measure the size of a given nS{Λ}, we can proceed to count the numbers existing within that interval at that stage of construction (Table 1).
The following chart compares the quantity of numbers (embedded values) existing in two different numeric structures of the same shape (real/positive/uniform/infinitely extensive-intensive), at three different construction stages and within three different intervals:
| Stage | Interval | |||||
| (0,1] | (0,2] | (0,3] | ||||
| nS {N/N} | nS{N√N} | nS {N/N} | nS{N√N} | nS {N/N} | nS{N√N} | |
| 4 | 6 | 1 | 9 | 9 | 10 | 10 |
| 8 | 22 | 1 | 32 | 41 | 36 | 46 |
| 15 | 72 | 1 | 108 | 163 | 120 | 175 |
Table 1. The give table shows compares the quantity of numbers (embedded values) existing in two different numeric structures of the same shape (real/positive/uniform/infinitely extensive-intensive), at three different construction stages and within three different intervals.
This method cannot give the total size of a complete infinite numeric structure because there is not such a thing as a complete infinite numeric structure; but it provides accurate information about the way infinite intensive and extensive-intensive numeric structures grow, which could be more useful than saying that their cardinal is N0, N1, N2, &nS; and, certainly, it makes much more sense.
Shape and potential are two different and closely related qualitative properties of numeric structures. Size, on the other hand, is a quantitative method for comparing different numeric structures of similar shape and potential.
Questions for further developments on the theory of numeric structures
Some interest questions arise from the initial development of the Theory of Numeric Structures:
Unspecifiable values: I have proved that between any two real numbers there exist at least one unspecifiable value; a segment of the real value-line (open interval) for which no utter expression can exist. From that, some hypotheses can be presented for confirmation or refutation:
Υ hypothesis: There exists an unspecifiable value in the real value-line called the unspecific particle (Υ), for which the following is true:
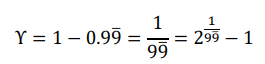
Υ-function hypothesis: All unspecifiable values in the real value-line can be defined as a function of the real numbers as follows:
u=x+Y
v=x-Y
Where (u) and (v) are different unspecifiable values, (x) is a real number and (Υ) is the unspecific particle.
Hypothesis of non-determinability: Any operation that implies the addition of two or more unspecifiable values of the same sign is undefined. E.g. 2Υ and −2Υ are undefined.
Theorem of parity in complex numbers: I have shown how the Theorem of parity is applicable to any numeric structure that has its domain within the real or imaginary value lines. Does it apply the same way to numeric structures that have their domain in both the real and the imaginary value lines?
Acknowledgment
I must express my gratitude to the people whose valuable comments and thoughts were an important contribution to this work; especially to Allen Bogart, Wolfgang Mückenheim, Adam Polak and Andrzej Burkiet.
References
- Mückenheim, Wolfgang. Transfinity: A Source Book. 2023.
- Warren Dauben, Joseph Georg Cantor. His Mathematics and Philosophy of the Infinite. Princeton University Press, 1979.
- Therrien VL. Wittgenstein and Labyrinth of ‘Actual Infinity’: The Critique of Transfinite Set Theory. Ithaque. 2012; 10:43-65.
- Zelcer M. AA Fraenkel’s Philosophy of Religion: A Translation of “Beliefs and Opinions in Light of the Natural Sciences”. Hakirah: The Flatbush J Jewish Law Thought. 2011; 12:209-32.
- Weber Z. Transfinite numbers in paraconsistent set theory. The Review of Symbolic Logic. 2010;3:71-92.
- Dauben JW. Georg Cantor and the origins of transfinite set theory. Scientific American. 1983;248(6):122-131.
- Therrien VL. Wittgenstein and Labyrinth of ‘Actual Infinity’: The Critique of Transfinite Set Theory. Ithaque. 2012;10:43-65.
- Rodych V. Wittgenstein's critique of set theory. South J Philos. 2000;38(2):281-320.
- Sward GL. Transfinite sequences of axiom systems for set theory. University of Illinois at Urbana-Champaign; 1967.
- Isaacson D. The reality of mathematics and the case of set theory. Truth, reference, and realism. 2011;1-75.

