Research
, Volume: 13( 2) DOI: 10.37532/2320-6756.2025.13(2).400Unification of the Physics Laws since New Theory of the Transformations Relativistic of Micro-World
- *Correspondence:
- Efrain Pantaleon Matamoros
Department of Science and Technology, Federal University of Rio Grande do Norte, Natal, RN, CEP: 59072-900, Brazil
E-mail: efrain.pantaleon@ufrn.br
Received: February 24, 2024, Manuscript No. TSPA-23-113825; Editor assigned: February 27, 2024, PreQC No. TSPA-23-113825 (PQ); Reviewed: March 14, 2024, QC No. TSPA-23-113825; Revised: March 07, 2025, Manuscript No. TSPA-23-113825 (R); Published: March 14, 2025, DOI. 10.37532/2320-6756.2025.13(2).400.
Citation: Matamoros EP. Unification of the Physics Laws since New Theory of the Transformations Relativistic of Micro-World. J Phys Astron. 2025;13(2).400.
Abstract
The unification of the laws that govern the physical phenomena, it has been research topic for different scientist generations. These investigations have been accomplished by different methods, but mainly in this century with the application of the quantum mechanics which governs the phenomena of the microworld and tends to assume the laws of the macro world. The function proposed for the unification of the physical processes, is achieved modifying the interpretation that gives origin to the equation of Einstein-Kolmogorov, extrapolating it from the infinitely small to the infinitely large; making possible the obtainment of a unique function that contains the physical laws, taking into account the parameter existence time for each physical state.
Keywords
Physical phenomena; Macro-world; Physical processes
Introduction
Currently, the image that is presented of our Universe is of a heap of galaxies that are separated mutually, this means that a long time ago, around 1.5 × 1011 years [1], the matter and energy were concentrated in a single point, that exploted and was expanded. This explosion is known by the name of the Big Bang.
Einstein and Kolmogorov worked on the diffusion of a gas in certain (Brownian movement), finding out the function, of puntual source, that corresponds to the particle concentration this function equals Ψ(m, t, m0 ,t0); for moment t where m0 it is the starting point for t0, what corresponds to the unitary mass, them:
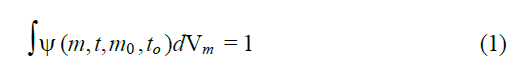
in case t> t0 The initial particles concentration in t0 equals φ(m) and the particles concentration for t>t0 equals φ(m,t)
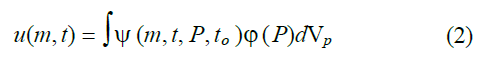
this equation is valid for t0<θ< t. This function solves the Einstein-Kolmogorov equation
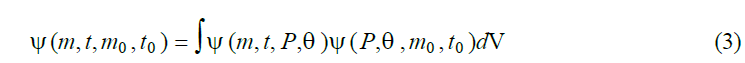
The solution of this equation satisfies a partial derivatives equation of the parabolic type, which can be generalized to other phenomena.
The fundamental motivation to relate both problems is to generalize an equation conceived for the micro world and to try to extend it to the phenomenon of the Big Bang, similar result should be obtained for both problems due to their characteristics, in both phenomena it is clear that for t0 these an energy and an initial mass concentration in a point x0.
The principal objective of this paper is to find a function that could explain the phenomenon that gave origin to our Universe, and if possible the one that could generate the physical laws that exist.
Model and solution of the equation
The function (3) satisfies an quasilineal equation of the parabolic type, which contains an equation of the type [2].
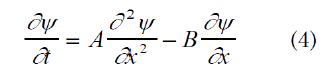
considering A=A(x,t) and B=B(x,t) the equation is converted into quasilineal, the solutions of this type of equation are achieved by the method of the finite differences. In this occasion the solution in a analytical way is sought, using as condition that the function contains the laws that govern the of the macro and microworld phenomena and that the relationships are obtained from the Relativity Theory, which would demonstrate that it is an unique function for the solution of the physical phenomena.
Materials and Methods
Physical model and mathematics conditions
Denomination:
W: External work.
φ=φ(r, t): Initial State.
Ψ=Ψ(r, t): Final State.
Eo: Kinetic energy of the particles or bodies in the initial state
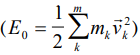
E: Kinetic energy of the particles or bodies in the final state
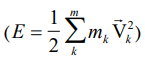
τ: Own existence time of each state.
Model and physics conditions
• Every isolated system in thermodynamic equilibrium do not separated of it spontaneously, therefore as a condition for transformation in a physical system (Universe) these must be an external work (If W=0 then Ψ=0, if W→∞ Ψ=φ))
• Every system or physical state presents an own existence time during which it maintains its properties (If τ>t macroworld: The transformations occur slowly; if τ=t then Ψ=0; if τ<t microworld: The transformations occur very fast)
• Each state is is in constant transformation in its own space because its submitted to internal and external forces.
Solution
Using the following function as a possible solution
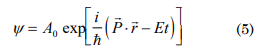
which corresponds to a function that characterizes the flat waves, and is used as the solution of the Schrödinger equation to simulates the electromagnetic waves. Obtainment of the equation that governs the state in partial derivatives. Considering:
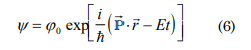
derivating with respect to time obtain
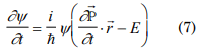
derivating with respect to the coordinate one can obtain
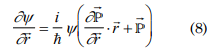
seeking 2nd derivative with respect to r
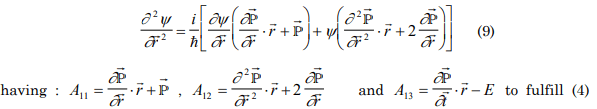
p=p (r,t) then accomplishing mathematical arrangements between the equation (7) and (9) one can write the following equation
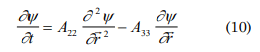
A22=A13/A12 and A33=iA11A13/hA12 quasilineal equation of the parabolic type.
Considering: P=iE20τ/|√τ2-t2|Wv where v is the particles or bodies speed in the initial state.
If one considers that W depends of and t, derivating P in:
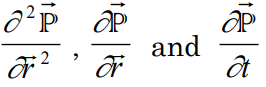
And
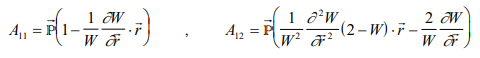
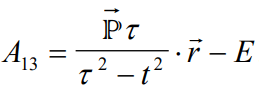
If the coefficients A22 and A33 are not constant. If A33→ 0 and A22 is constant then the equation takes the easiest form of heat conduction, phase transformations, etc.
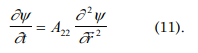
Analysis of the principal function
Correspondence with condition # 1
The function fulfills: W→0 Ψ (r,t )=0, W→∞ Ψ(r0,t0)= Ψ0 (r0,t0)
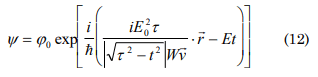
Correspondence with condition # 2
Macro world: τ>>t, then |√τ2-t2|=τ
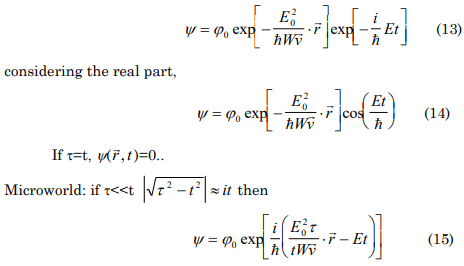
where E20τ/tWv is expressed in Kgms-1.
Correspondence with condition # 3
The function (12) represents the state transitions. According to the model all the states are in constant transformation, and as a consequence takes the form
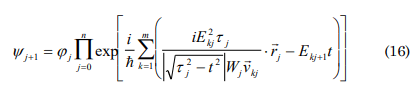
where k is the number of particles or the bodies of the state j, this function is correct if a closed system is considered, in case it is open the state overlapping should be considered, and then
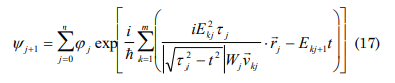
the functions (12), (16) and (17) have its practical application in the phase transitions, for all type of material, W represents the temperature or the deformation load to which it is submitted [3].
Relationship to other physics laws
Deduction of the Newton law
Departing from function (13) and considering its real part for a body, the relationship: cos (Et/h)=C, can be considered for E→0
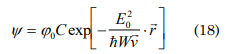
knowing that E20=1/2 E0 P.v. then
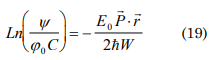
Inducing that P. r=I (Escalate independent of time)
According to the quantum mechanics, for the quasiclasic case Bohr Somerfield, propose P. dx=nπh where for values of a and P. r=nπh is fulfilled.
FFor that case P. r=constant then:
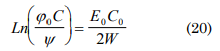
considering the external work as W=F. Δr and
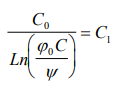
then F. Δr=1/2C1E0 derivating with respect to time in both members
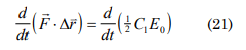
If F does not depend of time
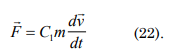
Considering in (20) W=C1E0, E=nhv and U(r)=e where is the electrical potential and W/C1=W1 then e=nhv-W1, which is the Photoelectric effect law.
Deduction of the equation of Schrodinger
Considering in the function (15) its real part and E0>W then
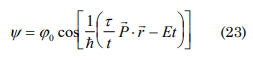
making mathematics operations the following expression is obtained
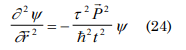
which represents a quasilineal equation for the micro world.
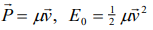
If the function (24) is taken considering
and knowing that the electron does not change during the test time, (argument used in the existing theories) then t=τ and E=E0 therefore E=E+U. Replacing in (24) the equation from Schrodinger is obtained
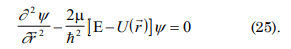
This can be demonstrated taking as a starting point the finding of a general equation which contains the Klein-Gordon equation and tends to obtain the Schrödinger equation.
We consider of the function (12) a particle that is not transformed during the measuring time, therefore the function can contain only the energy term in time:
Ψ= exp[-(iEt/h)] considering E=mc2 one can obtain:
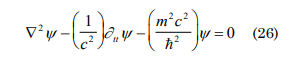
nevertheless, the equation can be even more general considering the exposed function in this paper being of the type Ψ= φ(r,t) exp[i/h(P(r, t)-Et)], consequently (r, t)= φ(r, t) exp[i/h(P(r, t)], substituting Ψ=(r,t) exp[-iEt/h)] in the previous equation (26) one can obtain:
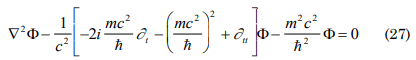
which represents a general equation for considering =exp[i(kx-ωt)] where k=2π/λ and λ is the wavelength. Working in low-frequency solutions where the condition ω<<mcr/h is fullfilled the term in the general equation is made negligible and is obtained the Schrodinger equation for the partuicle free [4].
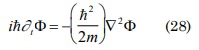
the previous demonstration it is clear that the function is also a solution of the Klein-Gordon and Dirac equation.
Deduction of the theory of the relativity, and relativist correction of the energy. The Theory of the Relativity does not take into account the existence of structures in the elemental particles. Any extension of the particle in the space, contradicts this theory. At present there are direct experimental results that demonstrate the presence of structures in the particles and there are different procedures elaborated in these studies [5].
Using the function (15), that takes into account different systems, with different times and considering its real part:
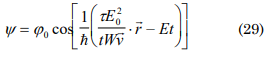
if the whole state passed to another Ψ/φ0=1, cos(z)=1 if z=2nπ then
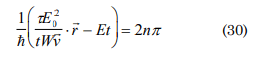
knowing that E20=1/2P. vE0, E0=1/2mv2
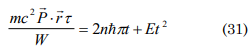
differentiating with the time and considering according to what was established previously P. r=h
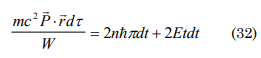
imposing the mass as invariable and v as the final state speed one can obtain:
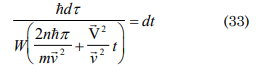
according to Bohr-Somerfield ΔP. Δr=2nhπ, mv2t=2nhπ
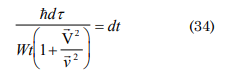
assuming the external work as
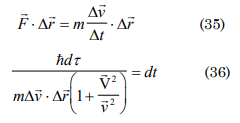
if the initial state speed is v=c then according to [6]:
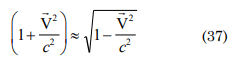
which is valid, according to the postulate of the relativity about the speed of light, where c > >>>v for all the cases β=vc→0 therefore
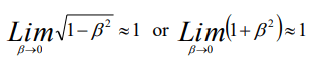
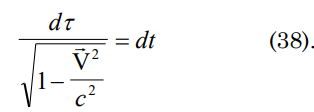
For the demonstration of the energy equation we will assume that the particle does not change during the measurement time, then τ = t. From the function (12) the equation (30) is obtained, calculating E02 from (30) for the case of the electron:
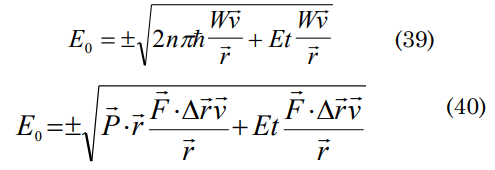
taking v=c, considering the point where is fulfilled: Δr=r, Δv=c and Δt=t. Knowing that
E=mc2, P . r = 2nπh and W=mΔv/Δt. Δr, and grouping terms
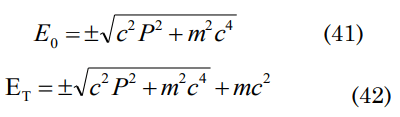
results evident that the kinetic energy presents negative and positive values
Results and Discussion
According to the proposed model, the different stages of our Universe occurred due to the existence of the external work (1st postulate of the thermodynamic), existing for each one an own existence time exposed in the work of Bakulin, Kononovic and Moroz. The laws known until the moment do not describe the processes for t=t0 where t0<10-43 seconds, and in the era of Planck where emerge the gravitation quantum (gravitons).
With the reported values by Bakulin, et al., Schramm one can calculate approximately the existing work during each stages, for different existence or evolution times of the Universe. This can be calculated using the following expression deduced from (36)
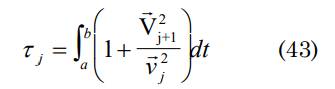
supposing for the era of Planck that the speed of the gravitons is c, i.e., the same for the era of the GUTs inflation and leptons; and taking the speed for the radiation as 0.91 c and 0.651 c for the era of the matter (proposed in the work of Silverman). To simplify the calculation, it of W one can consider the function (18), taking C=1 where cos (Et/h=cos(2nπ) and P . r =h; extrapolating for all the stages
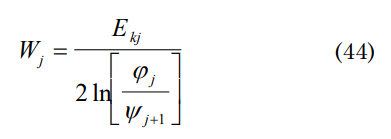
where φj and Ψj+1 represents the densities of the states Ekj=kTj, to facilitate the calculation it [7,8]. For the era of Planck, it can be considered that E0=kT0=1.38 × 109 J, supposing that the internal energy does not vary in the first seconds of the explosion, the results can be observed in Table 1.
| Era | τ(sec.) | T (sec.) | T0 (K) | Tf (K) | φj (gcm-3) | Ψj+1 (gcm-3) | Wj (J) |
| Planck | 2 × 10-43 | 0 | 1 × 1032* | 1 × 1032 | 1 × 1095* | 1 × 1094* | 3 × 108 |
| GUTs inflations | 2 × 10-35 | 1 × 10-43 | 1 × 1032 | 1 × 1028 | 1 × 1094 | 1 × 1078 | 2 × 107 |
| 2 × 10-5 | 1 × 10-35 | 1 × 1028 | 3 × 1012 | 1 × 1078 | 1 × 1016 | 5 × 102 | |
| 1.8 × 10-4 | 1 × 10-5 | 3 × 1012 | 1 × 1012 | 1 × 1016 | 1 × 1014 | 4.5 × 10-12 | |
| Leptons | 1.8 × 10-3 | 1 × 10-4 | 1 × 1012 | 3 × 1011 | 1 × 1014 | 1 × 1012 | 1.5 × 10-12 |
| 0.39 | 1 × 10-3 | 3 × 1011 | 2 × 1010 | 1 × 1012 | 1 × 107 | 1.8 × 10-13 | |
| 19.8 | 0.2 | 2 × 1010 | 1 × 1010 | 1 × 107 | 1 × 104 | 2 × 10-14 | |
| Radiation | 180 | 10 | 1 × 1010 | 1 × 109 | 1 × 104 | 1 × 102 | 1.5 × 10-14 |
| 5.4 × 1013 | 1 × 102 | 1 × 109 | 4 × 103 | 1 × 102 | 1 × 10-21 | 1.3 × 10-16 | |
| Matter | 1.8 × 1015 | 3 × 1013 | 4 × 103 | 30 | 1 × 10-21 | 1 × 10-27 | 1 × 10-21 |
| Note: The values marked by (*) were assumed to facilitate the calculation. | |||||||
Table 1. Principal stages of the evolution of the universe.
Using function (16) one can calculate the initial dimensions of our Universe considering t→0:
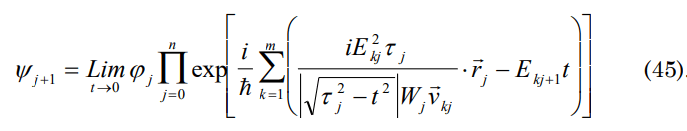
Accomplishing the mathematical arrangements and considering
M=mk mk the total mass of the Universe we have:
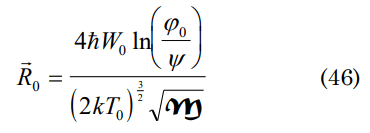
this function indicates that the dimensions are R0=(M)-1/2 Ln(z) ×10-36 m, which is insignificant, but one observer being out of the Universe system, would observe the polarisation of the vacuum for t>t0, a topic of investigation at present [9-11].
Using equation (16) again the law of movement of our Universe can be found and that for t being t>>>τ then |√τ2-t2|=√-1(t2-τ2)=i|√t2-τ2| using the expression of P. r=Pr cos and assuming for simplification cos=1 , from the expression (45).
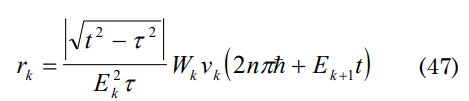
one can find the life time of our universe if a relationship as dr/dt=0 is obtained:
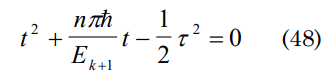
considering t = γτ one can obtain t=2nhγ2/Ek+1(1-2γ2) and t=0 from where is deduced that for time being always positive the condition fulfilled 1-γ2 ≥ 0 should be having that for this work γ=v2/v2+v2 then from the inequality is obtained that the speed of the initial state (V) must fulfill V ≥ 0.2v so that the transformation occurs, substituting the value of time in the expression that denotes the dimensions of the universe then:
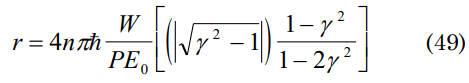
where for V=0, r→∞ from the previous expression is also possible to deduce the undetermination equations of Heisenberg, those which gave origin to the quantum mechanics.
The equations of the General Theory of the Relativity can be written as:
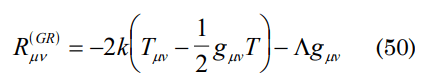
Making use of the following expression
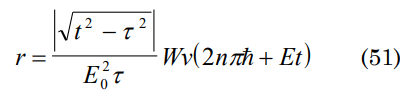
and considering t=γτ then |√t2-τ2|/τ=|√γ2-1| making Et=2nπhF(γ) and r2:
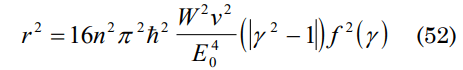
where f2(γ)=[1+F(γ)]2 pass to a four-dimensional space of the Minkowski type where is valid that: r2=c2t2-r2α, v2=γ2 u2α+c2 where rα is the 4-vector of position and uα of speed then one can obtain:
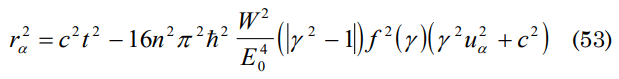
it is fulfilled that u2α=-c2, multiplying the second term by t2/t2 and applying again an expression of the type E0t=2nπhF(γ*),
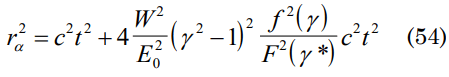
therefore as c2t2=invariant, R(GR) ββ=c2t2, aαµaαv=gµv y aβµaβv=gµv
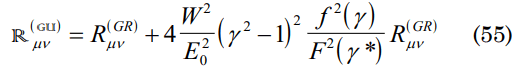
R(GU) µv=R(GR) µv, then γ2-1=0 and this is fulfilled if β2→0 consequently c>>V, that is the postulate of the relativity theory.
From this function it can be induced that the expansion or compression of our Universe is given by the kinetic energy of the bodies. To simplify the expression, it can be described in the following form:
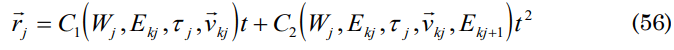
if Ekj+1 t=2nπh then
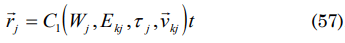
Figure 1 shows the law of movement from t=0 sec(R(0)=3,12 × 10-32 m) to t=1 × 1015 sec(R(t)= 3,51× 1021 m) era of the radiation, considering the reported values in Table 1 and using (47).
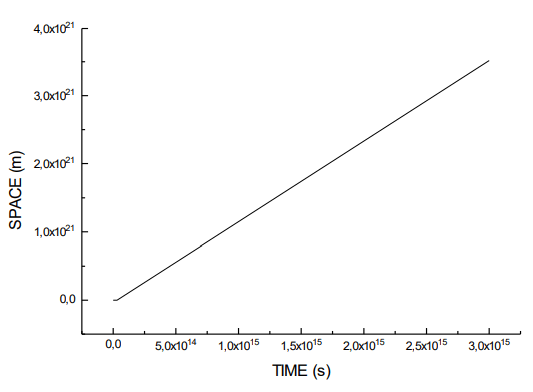
FIG. 1. Evolution of the universe.
The function (47) can be used to obtain the initial density of our Universe, calculating the radio for t=0 sec, and knowing an estimate as exact as possible of the total mass. Accomplishing mathematical arrangements and knowing the real space, the time elapsed from its origin can also be calculated. Considering t>>>τ for all t then making t→0 in (47) is obtained
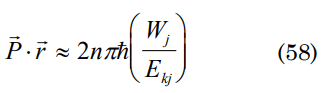
hence it can be induced that P . r ≥ h/2 Heisenbe g´s equations that pe mit us to say that the laws that govern the microworld do not take in consideration the term 2nπ (WjEkj), that it denotes the interactions of the particles with external agents as the devises used in quantum mechanics measurements or vacuum polarizations.
Conclusion
The functions proposed, does not correspond to a wave. They are state functions, that tend to unify the known physical laws. The model and the induced expressions do not contradict the practical results, due to the fact that they contain the equations that govern these results, and for its deduction have not been created new concepts. The functions proposed can be deduced (be induced) starting from other phenomena, in which the arriving forces for the transformations of a physical state, be internal energy and the external work. The state functions permit deduce the interactions between states of the matter that they can be transformed one into another if the initial and final parameters of each state are known.
Acknowledgements
This work has been possible by the disinterested collaboration of many colleagues, that they have helped me in the draft as well as in achieving with their difficult you ask that could argue my work as well as my knowledge. Desire to thank to: U.Ordoñez, J.Alvarez, Jr.Alvarez, F. Martinez, I. Castells, A.Batista, L. Pereiro, A.M. Folgueira, J Caesar, E. Chavez, S.C.O'farril and F.M.Zumba.
References
- Silverman AN. Resolution of a cosmological paradox using concepts from general relativity theory. Am J Phys. 1986;54(12):1092-1096.
- Samarsky T, Tijonov AN. Equations of Mathematical Physics. Editorial Mir, Moscu. 1972.
- Pantaleón E. Right Author Register 01110-1110 CENDA, Cuba, Unpublish, Ref: The deduction of functions to must the physics unifications laws. 1996.
- Flatté SM. The Schrödinger equation in classical physics. Am J Phys. 1986;54(12):1088-1092.
- Lev Davidovich L, Lifshitz EM. Abbreviated theoretical physics course: Quantum mechanics. Book 2. Mir; 1974.
- Bakulin PI, Kononovich ?V, Moroz VI. General Astronomy Course. Mir Editorial; 1987.
- Schramm DN. The early universe and high?energy physics. Phys Today. 1983;36(4):27-33.
- Szhwarzschild B, Desperately Seeking Superstrings. Phys Today. 1986;39(5):17-20.
- Wilkins D. Gravitational fields and the cosmological constant in multidimensional Newtonian universes. Am J Phys. 1986;54(8):726-31.
- Vetterli D, Boeglin W, Egelhof P, et al. Effects of vacuum polarization in hadron-hadron scattering. Phys Rev Lett. 1989;62(13):1453.
[Crossref] [Google Scholar] [PubMed]
- Lederman L. Richtmyer Lecture: Unification, grand unification, and the unity of physics. Am J Phys. 1986;54(7):594-600.

