Short communication

, Volume: 13( 1) DOI: 10.37532/2320-6756.2025.13(1).354

• View PDF
• Download PDF

Fermat's Last Theorem Derived in a Direct Computation

*Correspondence:

Pawel Jan Piskorz
Department of Physics, Medical University of Lodz, Lodz, Poland
E-mail:paweljanpiskorz@gmail.com

Abstract

We propose a procedure which all ows to compute the only accept able natural exponents of the positive integers X, Y, Z in the equation of the Fermat’s Last Theorem. We use the approach similar to the one applied in computing of the expected value and the standard devia tion of number of successes in Bernou lli trials pr esented by Kenneth S. Miller.

Keywords

Fermat’s Last T heoremheorem; Diophantine equations equations; Bernoulli trials

Introduction

We write the equation from the Fermat’s Last Theorem [1]

in which X, Y, Z ∈ Z+ are integers greater than zero and N ∈ N is a natural number [2-5].

Without loss of generality we rewrite Equation (1) as

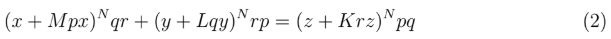
with p, q, r ∈ R and M, L, K ∈ N. Now we set q=1 and r=1 with Y=y+Ly and Z=z+Kz obtaining

with X=x+Mpx. We have introduced a real number parameter p ∈ R the value of which will be later set to 1. The number M ∈ N is a natural number. With such assumptions we must have x ∈ {1/(M+1), 2/(M+1), 3/(M+1), . . .} in order for the variable X to assume integer values as required in Equation (1).

E.g.: If M=1, p=1, x ∈ {1/2, 2/2, 3/2,. . .} then X={1/2+1·1/2, 2/2+1·2/2, 3/2 +1·3/2, . . .} what gives X ∈ {1, 2, 3, . . .};

If M=7, p=1, x ∈ {1/8, 2/8, 3/8, . . .} then X={1/8+7·1/8, 2/8+7·2/8, 3/8 +7·3/8, . . .} what gives X ∈ {1, 2, 3, . . .};

We always arrive at X ∈ {1, 2, 3, . . .} for any natural number M and p=1, i.e., we have ensured that always X ∈ {1, 2, 3, . . .} no matter which natural number M we take into account. Similarly, we can ensure that Y and Z are also integers greater than zero appropriately choosing natural number parameters L and K and appropriately real numbers q and r in Equation (2).

Computations

We take partial derivative of both sides of Equation (3) with respect to p

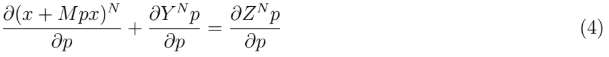
We compute the partial derivative of (x + Mpx)N as follows

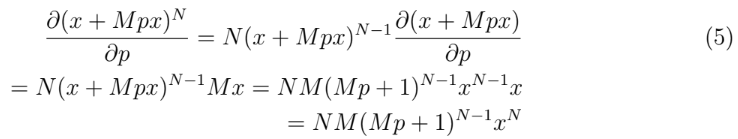
We receive a new Equation (6)

in which we can set the parameter p=1 obtaining

If we set p=1 in Equation (3) on the other hand, we obtain

We compare the coefficients at the term with x^N in Equations (7) and (8) receiving a constraint equation for N

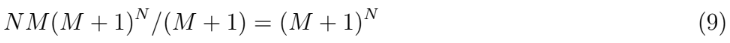
and therefrom we obtain the values of exponent N as a function of M

Quite similarly we can arrive at the formulas for N as a function of L

and for N as a function of K

Conclusion

We have started with the Equation (1) with assumption that X, Y, Z are positive integers and N is a natural number. We received the system of three constraint Equations (10), (11) and (12) for the four unknowns M, L, K and the number N. It means that one unknown among the four ones must assume two integer values. We see below that it is the variable N.

For N(M) we have

Quite similarly we can compute N(L) and N(K). We can state that with our assumption of having N ∈ N we have to reject all N(M), N(L) and N(K) solutions which are not natural numbers. Our fourth unknown is N equal to either 1 or 2 what is in perfect agreement with the Fermat’s Last Theorem.

Acknowledgments

This article is in honor of American mathematician Kenneth S. Miller. Due to his technique of computing the expected value and the standard deviation of number of successes in Bernoulli trials we were able to obtain our results.

Author would also like to thank an anonymous student without whom it would take longer to write this paper and who suggested placing the number p next to symbols YN and ZN in Equation (3) while the author was working on the universal expression of the natural number X using rational number x, natural number M and a real parameter p for partial differentiation.

The author received funds from PFRON (State Fund for Rehabilitation of Handicapped Persons) allowing the purchase of a laptop computer on which this publication has been written.

References

1. Kenneth S. Miller, Engineering mathematics, Dover Publications, Inc. 1956.
2. Edwards HM. Fermat's last theorem. Sci Am. 1978;239(4):104-123.

   [Google Scholar]

3. Vandiver HS. On Fermat's last theorem. Trans Am Math Soc. 1929;31(4):613-642.

   [Crossref] [Google Scholar]

4. Vandiver HS. Fermat's last theorem: Its history and the nature of the known results concerning it. Am Math Mon. 1946;53(10):555-578.

   [Crossref] [Google Scholar]

5. Dickson LE. Fermat's last theorem and the origin and nature of the theory of algebraic numbers. Ann Math. 1917;18(4):161-187.

   [Crossref]