Review

, Volume: 13( 2)

• View PDF
• Download PDF

What is the Event Horizon of a Black Hole?

*Correspondence:

Tadeusz Pastuszek
Department of Physics, Medical University of Silesia, Katowice, Poland
E-mail: tadeuszpastuszek@poczta.fm

Abstract

In this study, the conventional understanding of the event horizon in black holes within the framework of Einstein's general theory of relativity is reevaluated. Contrary to the widely accepted notion that the event horizon acts as a physical barrier from which nothing can escape, it is proposed that it should instead be understood as an abstract mathematical concept, arising from a misinterpretation of escape velocity. Through detailed analysis, it is demonstrated that the gravitational field intensity at the event horizon is significantly lower than previously believed, challenging the existence of phenomena such as Hawking radiation which rely on the traditional concept of the event horizon as a one-way membrane. Utilizing relativistic formulas for the first and second cosmic velocities, the study shows that for any black hole, the escape velocities remain below the speed of light, regardless of the black hole's mass or radius. This ending implies that the concept of an insurmountable event horizon is not supported by the equations of general relativity. The paper concludes by suggesting that black holes represent a distinct state of matter characterized by high but night density and questions the traditional view of black holes within the cosmological narrative. Through rigorous mathematical analysis, this research challenges established paradigms and opens new avenues for understanding the nature of black holes and the fabric of the universe.

Keywords

Black hole's; Mass; Density; Radius

Introduction

In the polish version of wikipedia, there is the following definition of the event horizon: "The event horizon is a sphere surrounding a black hole or a space-time tunnel, separating an observer from events from which the observer can never receive any information. In other words, it is a boundary in space-time beyond which the escape velocity for any object or wave exceeds the speed of light in vacuum [1]. And no object, even light emitted from within the event horizon, can escape from this area. Anything that crosses the event horizon from the observer's side disappears."

So we have such a situation: As we approach a black hole, our escape velocity increases. At the event horizon of a black hole, the escape velocity matches the speed of light and upon crossing the horizon, the escape velocity would have to exceed the speed of light, which is known to be impossible to achieve. This conclusion arises from the Schwarzschild solution of Einstein's general theory of relativity [2]. This solution states that for a non-rotating black hole, in the form of a point mass singularity, the event horizon is a sphere with a radius:

Equation

Where R_Sch-that's what's called the Schwarzschild radius

G-gravitational constant

M-mass of the singularity

c-speed of light

In the definition of the event horizon, the concept of escape velocity is very important. Let's refer back to wikipedia again. "Escape velocity (also known as the second cosmic velocity) of a celestial body is the minimum initial velocity an object must have to leave the gravitational field of that celestial body, i.e., for the trajectory of its motion to be an open curve (hyperbola or parabola)."

Literature Review

Translating this into a more understandable language: Escape velocity is the speed that must be given to a massive object within a gravitational field for it to move away indefinitely [3]. What happens if such an object is given a velocity lower than the escape velocity? (We encounter this situation, for example, when we throw a ball into the air or shoot a rifle into the sky). Simply put, the object will move away from the source of the gravitational field and then return to it or orbit the celestial body on an elliptical orbit [4]. (To be more precise-it will move along a closed curve).

From the above, it follows that when we give a massive object below the speed of light on the event horizon, the object will leave the event horizon, but it won't reach infinity. Once it reaches a certain altitude, it will start to fall back just like a ball thrown upwards. Also, when we go below the event horizon, depending on the depth of descent, there are velocities (directed upwards) that are less than the speed of light but greater than a certain critical velocity. These velocities will cause the object to rise above the event horizon and eventually fall back [5]. The conclusions presented here stem from the equations of the general theory of relativity upon which the so-called Schwarzschild metric is defined.

One must realize that no mathematical model implies the existence of a mysterious "semipermeable membrane" called the event horizon. Further-more, no model proposing the mechanism of such a semipermeable membrane has been put forward. In this situation, the existence of the physical phenomenon known as Hawking radiation should also be questioned [6].

The hypothesis of the existence of a surface that allows everything to pass in one direction and nothing in the other is descriptively justified (without any mathematics) by saying that there is an immense gravitational field intensity at the event horizon of a black hole, which causes space-time to be curved to such an extent that nothing can escape from it. Additionally, when referring to "immense gravitational field intensity," no specific numbers are provided.

In that case, let's try to calculate the gravitational field intensity at the "event horizon" of a sample black hole with a Schwarzschild radius of 1/2 light-year. From formula (1), it follows that the mass of such a black hole is approximately 3.185 × 10⁴² [kg]. The average density of such a black hole is about 7.183 × 10⁻⁶ [kg/m³], which is over five orders of magnitude smaller than the density of air at sea level. The gravitational field intensity (gravitational acceleration) at a distance of the Schwarzschild radius from the center of such a black hole is approximately 9.5 [m/s²], which is less than that on the surface of the earth.

Of course, despite such a small gravitational field intensity, according to the equations of general relativity, it still follows that at the "event horizon" of such a black hole, the escape velocity equals the speed of light. According to these equations, it is impossible to impart any object with a velocity that would allow it to escape to infinity. However, these equations do not imply that the so-called event horizon constitutes a physical barrier. The concept of escape velocity is simply misinterpreted in this context.

If the mass of this black hole were evenly distributed gas within its interior, the gravitational field intensity along the radius would decrease linearly from the value of 9.5 [m/s2] to zero at its center. However, if all the mass were concentrated at the center in the form of a singularity, the gravitational field intensity along the radius would increase (proportional to the inverse square of the distance) from 9.5 [m/s²] to infinity at its center. It is in the singularity that the gravitational field intensity has an infinite value and nothing can escape from it. However, the singularity has no interior; it is just a point. Nonetheless, it is essential to remember that a singularity is an abstract mathematical concept. All physical theories, including general relativity, collapse in a singularity and there is no empirical evidence that such a physical object can exist.

In light of these considerations, we can imagine a celestial body orbiting such a black hole in an ellipse partially submerged under the Schwarzschild sphere, where it alternates between falling below the "event horizon" and emerging from it over time. Ultimately, it can be concluded that the event horizon of a black hole, according to the general theory of relativity, is a geometric locus of points where the escape velocity, understood as the second cosmic velocity, equals the speed of light. Therefore, the event horizon is not a physical barrier but rather an abstract mathematical object.

Let's take a closer look at the assertion that there are points in a gravitational field where the escape velocity equals the speed of light. From the definition of escape velocity (the second cosmic velocity), it follows that this is the velocity that must be imparted to a small test object (with a mass at least several orders of magnitude smaller than that of the celestial body on whose surface it resides) to make it escape to infinity. According to the principle of energy conservation, if such a small object falls from infinity onto the celestial body, it will attain the escape velocity at the surface of that body. At this point, a reflection arises: No object with mass falling from infinity towards a black hole could cross the event horizon because it would have to reach the speed of light, which, according to our knowledge, is impossible. (Note: We wouldn't have to wait for something to fall from infinity; it would be enough to give the test object the appropriate velocity towards the black hole).

To break out of this impasse, all we need to do is apply a simple maneuver. We have to assume that gravitational charge consists solely of rest mass and kinetic energy is just a component of what is known as inertia. (Inertia is a parameter that appears in the second law of Newtonian dynamics). Rest mass is a Lorentz invariant, meaning it has the same value in all reference frames. However, kinetic energy depends on the reference frame. If we want to unify gravitational interaction with the electric one, then the gravitational charge, just like the electric charge, must be a Lorentz invariant.

After assuming that rest mass is the gravitational charge, relativistic formulas for the first and second cosmic velocities can be easily derived. From these formulas, it follows that a black hole of arbitrarily large mass and arbitrarily small radius greater than zero has first and second cosmic velocities less than the speed of light. The derivations of these formulas are presented below.

Discussion

Relativistic formulas for the first and second cosmic velocity

As mentioned earlier, inertial mass in the equation of the second law of Newtonian dynamics consists not only of rest mass but also includes the kinetic energy of the body undergoing acceleration. Assuming that gravitational charge consists solely of rest mass instantly resolves a problem that troubled physicists for some time. Inertia mass from the second law of dynamics is not the same as the mass appearing in Newton's universal law of gravitation formula. What then is the inertial mass from the second law of dynamics? After the announcement of Einstein's Special Theory of Relativity (STR), the second law of dynamics underwent a transformation. Its relativistic version looks as follows:

Equation

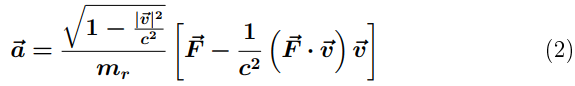
where m_r is the rest mass of the body, and are its velocity and acceleration, is the force acting on the body, c is the speed of light and a dot denotes the scalar product of vectors.

If we take into account that the total energy (Et) of a body is given by:

Equation

then equation (2) can also be written as:

Equation

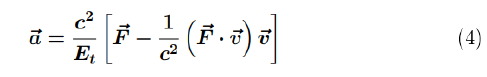
Formula (3) for the total energy applies to a body at absolute zero temperature and without angular momentum. Formula (2) also applies under these same conditions. Therefore, formula (4) is appropriate, where the total energy of the body can include not only the rest mass, but also the temperature and the kinetic energy resulting from the velocity and angular momentum.

Formula (4) can be transformed to give the force vector in terms of the acceleration vector:

Equation

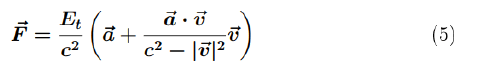
In equations (4) and (5), we see that the concept of inertial mass has become ambiguous. It is not possible to unambiguously indicate the proportionality coefficient between the acceleration vector and the force. We have a complex relationship related to the directions of acceleration, force and velocity vectors.

The first cosmic velocity is the velocity of a satellite moving in a circular orbit with a radius of R around a central body, where R is also the radius of that body. In such a circular motion with velocity v, the centripetal acceleration is given by the formula:

Equation

The centripetal force acting on a body moving in such an orbit, according to the relativistic form of the second law of dynamics (5), is given by:

Equation

(As velocity and acceleration vectors are perpendicular in this case, the second term in parentheses in formula (5) equals zero). If we neglect the temperature and any possible angular momentum of a satellite with rest mass mr, then formula (7) can be written as:

Equation

After substituting the acceleration from (6) into (8), we obtain the relativistic form of the formula for the centripetal force:

Equation

On the other hand, from Newton's law, it follows that the force acting on a satellite moving in a circular orbit of radius R around a central body of rest mass Mr is given by:

Equation

where G is the gravitational constant, equation (9) and (10) yield the following equation:

Equation

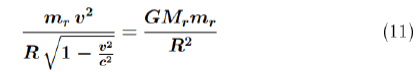
The solution of this equation is the relativistic formula for the first cosmic velocity:

Equation

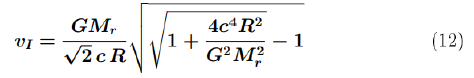
It is necessary to verify what value this formula gives for earth. Assuming the mass of earth to be 5.97219 × 10²⁴ [kg], the average radius of earth to be 6371008 [m], the gravitational constant to be 6.67428 × 10⁻¹¹ [m³/kgs²] and the speed of light to be 299792458 [m/s], equation (12) yields the value:

Equation

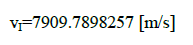
On the other hand, according to the previously used non-relativistic formula:

Equation

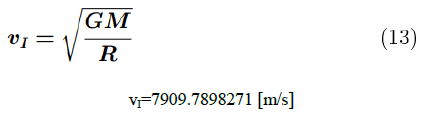
We obtained a result that differs just in the tenth significant digit. If the same calculations are performed, for example, for a neutron star with a mass of two solar masses and a radius of 12000 [m], according to formula (12): v_I=139868400 [m/s], while the traditional calculation yields-formula (13): v_I=148720918 [m/s]. This time, the first cosmic velocity calculated using formula (12) is nearly 6% smaller than that calculated using the currently used formula.

The function given by formula (12) is a continuously decreasing function in the range of r ∈ (0, ∞) and the limit of this function for r→0 is c. Therefore, it can be observed that for any massively compact black hole with a radius greater than zero, there exists a first cosmic velocity smaller than c.

Attention! For the Schwarzschild radius R_Sch=2GM/c², the first cosmic velocity according to formula (11) is v_I=187313486 [m/s], while according to the non-relativistic formula (12): v_I=211985280 [m/s].

On the other hand, in order to find the relativistic formula for the second cosmic velocity, one needs to calculate the energy that must be expended to move a test body with a rest mass mr from the surface of a celestial body with a rest mass Mr and radius R to infinity.

Attention! The second cosmic velocity is the velocity that must be imparted to a test body on the surface of a celestial body to allow it to escape to infinity, assuming that only these two bodies are present in space.

The work W required to move a test body to infinity is determined by the formula:

Equation

The relativistic formula for kinetic energy (Ek) is as follows:

Equation

After substituting the expression from formula (3) for Et:

Equation

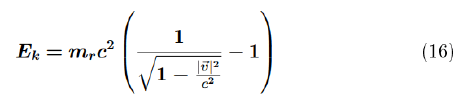
Therefore, one needs to solve the equation:

Equation

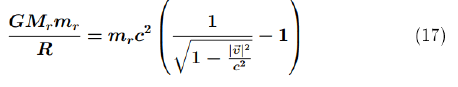
We have obtained the relativistic formula for the second cosmic velocity:

Equation

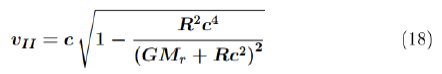
According to the equation, it follows that as the radius of the central body approaches zero, the second cosmic velocity approaches the speed of light regardless of the central body's mass. So, it is similar to the case of the first cosmic velocity: For any massive black hole with a radius greater than zero, there exists a second cosmic velocity smaller than c.

The second cosmic velocity for earth calculated according to equation (18) is:

vII=11186.1320431 [m/s]

Calculated using the non-relativistic formula:

Equation

is: v_II=11186.1320489 [m/s]

This time the difference appeared on the eleventh significant digit.

Note! For the Schwarzschild radius, the second cosmic velocity according to the relativistic formula (18) is v_II=223452 05 [m/s], while according to the formula (19): v_II=c.

Conclusion

The conclusion that black holes have their own escape velocities may seem surprising, but there is nothing unusual about this when one considers that there are no limits to the kinetic energy of massive objects. As the velocity of a massive object, in the reference frame of the central object, approaches the speed of light, its kinetic energy approaches infinity, while its gravitational charge (rest mass) remains constant. Therefore, one should ask oneself what black holes are, if they have no event horizon. Black holes are another state of matter with an extremely high, but finite density and are a manifestation of the universe's tendency to achieve maximum entropy.