Research

Received date: June 01, 2023, Manuscript No. TSPA-23-100914; Editor assigned: June 05, 2023, Pre-QC No. TSPA-23-100914 (PQ); Reviewed: June 19, 2023, QC No. TSPA-23-100914 (Q); Revised: August 31, 2023, Manuscript No. TSPA-23-100914 (R); Published: September 07, 2023, DOI. 10.37532/2320-6756.2023.11(9).379

Citation: Umar AK, Benjamin GA. Unified Dark Energy and Dark Matter from Rute as Different Manifestations of Vacuum Energy. J. Phys. Astron.2023;11 (9):379.

Abstract

Dark energy and dark matter are both described as different manifestations of vacuum energy within the framework of Rute. It describes gravitational inversion in a dimensional symmetry and interactions regulated by constraints. In this framework, the bare vacuum energy component exists in a gravitationally inert state where actual gravitational constant G_o=0G, while real particles oscillates between this inert state and the active state where G_o=2G. The background effect of neutrino substrates in the inert state makes G_o>0G in such state, causing the gravitation of virtual particles with positive pressure appearing as hot and cold dark matter. A non-zero component of vacuum energy also spills into the gravitationally active state as a cosmological constant form of dark energy. This is due to an energy density constraint and speed limit asymmetry between the two gravitational states that limits the capacity of the inert state to contain the entire vacuum energy component. This form of dark energy and dark matter, are both parameterized by a common asymmetry parameter Γ which is suppressed in deep gravitational potential wells. Rute predicts a testable Gravitational Wave Reheating (GWR) mechanism in which gravitational waves produce electromagnetic secondaries in the presence of negative pressure such as that from strong magnetic fields and even dark energy. This mechanism which may explain Fast Radio Bursts (FRBs) and Excess Radio Background (ERB) is also suppressed by the positive curvature of deep gravitational wells.

Keywords

Rute; Gravitational Inversion; Constraints; Cosmological Constant; Dark; Energy; Dark Matter; Neutrino Substrate; Speed Limit Asymmetry; Energy; Density Constraint; Gravitational Wave Reheating

Introduction

Dark energy has remained a mystery since its first discovery in 1998 [1,2]. Several independent observations including the Planck data indicates that dark energy constitutes about 68.3% of the total energy budget of the universe and driving its accelerated expansion [3]. This is in addition to the existing mystery of dark matter which appears to be some invisible but gravitating form of matter that clusters within and around galaxies. Dark matter makes up about 26.8%, while ordinary visible matter makes up 4.6% of the mass energy content of the universe.

The prolonged mystery of dark energy and dark matter which now accounts for about 95% of the gravitating energy content of our universe is not for want of efforts. Rather, it is an indication that their nature is deeply rooted in the way the universe actually works.

The simplest and most economical solution to explain dark energy already exists in the form of a cosmological constant term (Λ) earlier introduced by Einstein in his field equations and forms a key part of the standard model of cosmology known as the ΛCDM model (lambda cold dark matter). Λ readily comes from the expected gravitational effect of vacuum energy predicted within the framework of quantum field theory. The problem is the extremely large value of about 120 orders of magnitude expected from our understanding of quantum field theory compared to observation. This is the Λ problem [4].

Supersymmetry (SUSY) models readily provide a cancellation mechanism to reduce the bare Λ to a very small value but they suffer from excessive fine tuning. Also, supersymmetric partners of the standard model required for cancellation have not been found. There are some string theory models in which vacuum energy is simply relaxed, as well as some that resorts to anthropic consideration [5,6]. There are some models that makes the space time metric insensitive to Λ [7,8].

While the efforts to resolve the Λ problem intensified, there had been several alternative approaches that avoids the difficult problem of Λ. Prominent among them are quintessence which involves a slowly evolving scaler field, modified gravity models, unification of dark energy and dark matter [9-12].

The amount of theoretical and observational efforts that has been applied to understand dark energy and dark matter shows that they require new physics beyond the existing standard model of cosmology and particle physics. One of such attempts is the Rute model earlier published in its nascent form in focusing on dark energy and recently extended to include dark matter [13].

The Rute model, takes the speed limit asymmetry approach of resolving the Λ problem in which the bare vacuum energy component exists only in a gravitationally inert state where actual gravitational constant is zero. Real standard model particles oscillate between the gravitationally inert state and gravitational active state. A non-zero vacuum energy density then emerges in the gravitationally active state as dark energy due to a key energy density constraint and a speed limit asymmetry.

It describes dark matter as a different manifestation of the bare vacuum energy component that depends on the background effect of neutrino substrates on the gravitational constant. Neutrinos particularly cosmic neutrinos illuminates the background in the gravitationally inert state such that G_o>0G, making virtual particles gravitate with positive pressure and appear as cold dark matter. The model framework describes a gravitational inversion in a dimensional symmetry that doubles large spatial dimensions with microscopic partners while their interactions are regulated by constraints. These constraints such as speed constraint, energy density constraint, volume constraint, and force constraint, simply ensure a fixed absolute value of associated physical quantities across the various dimensions and states. This paper is organized as follows. Section 2 discusses the key dimensional symmetry that doubles the number of large spatial dimensions with microscopic partners. It also discusses the speed constraint, the two on and off gravitational states, and their speed limit asymmetry and density constraint, which is then applied in section 4 to solve the Λ problem. Section 3 discusses general relativity in extra dimension S₀ and explore it unique features of gravitational inversion as well as the chain of causality in gravitation. It is shown that the expansion of the time like S₀ dimension is equivalent to the curvature of our visible spatial dimensions S₁. Section 4 discusses the emergence of dark energy due to a speed limit asymmetry and energy density constraint discussed in section 2, while in section 5 the key reheating prediction is discussed. Section 6 discusses the gravitation of virtual particles which appears as dark matter due to the background effect of neutrino substrates on the gravitational constant in the inert state. Summary and conclusion follows in section 7.

Materials and Methods

Dimensional structure and symmetry in Rute

In the Rute framework, the number of large spatial dimensions is described by the dimension number Sn such that,

Sn = [4n–1]d                             (1)

Where n=0, 1, 2, 3…

n=0, corresponds to S₀ = -1d which is a time like spatial dimension that invisible due to speed constraint discussed in section 2.1.
n=1, corresponds to S₁=3d which is our visible spatial dimensions.
n=2, if it exists will correspond to S₂=7d which will also be invisible due to a force constraint that restricts standard model particles to the visible spatial dimensions S₁. Such invisible large dimensions however can be accessible by maximizing interactions in S₁ which minimizes the restricting interaction in S₂ according to equation 2.

F_P² = F_μ² + F_ν²                          (2)

Where;

F_P =Planck force.
F_ν =Resultant force a particle experiences in S₁ while F_μ is the restricting force of interaction in S₂ capable of making it inaccessible by standard model particles.

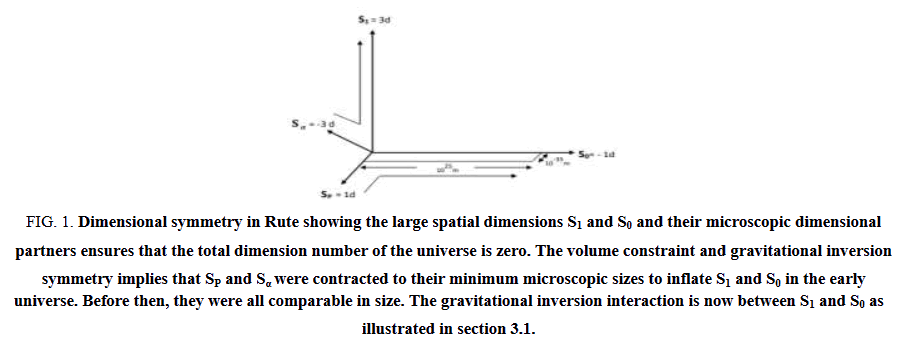
The dimensional symmetry in Rute doubles large spatial dimensions with microscopic dimensional partners with opposite dimension numbers such that the total dimension numbers of the universe is zero as illustrated in Figure 1. While the dimensional partner of S₀, is the Planck size S_P dimension, the dimensional partner of S₁ is denoted S_α and the possible dimensional partner of S₂ will be denoted S_β.

The volume constraint implies that the large spatial dimensions such as S₁ and S₀ where inflated in the early universe at the expense of their dimensional partners S_α and S_P until they contracted to their microscopic sizes becoming invisible.

This paper focuses on the S₀ dimension and its microscopic dimensional partner S_P as well as their interactions with the visible spatial dimension S₁.

Speed constraint and invisibility of S₀

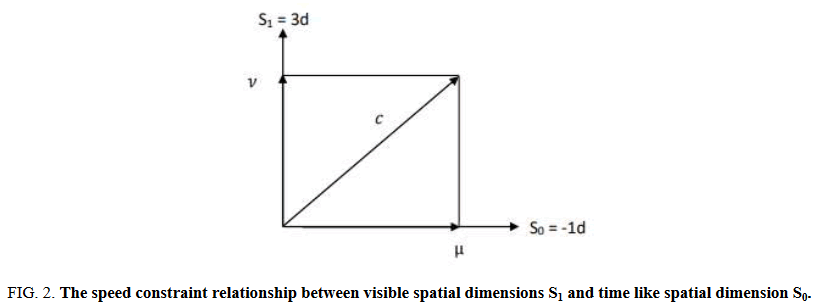
Despite its cosmic size, the S₀ dimension is invisible due to its time like behavior from the speed constraint illustrated in equation (2) and Figure 2.

The speed constraint requires that a particle’s velocity must always equal the maximum speed limit c in the S₁-S₀ dimension. Massless particles like photons have zero velocity component along S₀, while massive particles and antiparticles travel in opposite directions along S₀. This motion along S₀ is quantitatively equivalent to the passage of time such that,

c² = μ² + ν²                          (3)

Where;

μ=Particle velocity along S₀.
ν=Particle velocity along visible spatial dimension S₁.

When ν→0, for massive particles, μ→c and conversely, when ν=c for massless particles, μ=0 to satisfy the speed constraint. This suggests that time can be an emergent temporal dimension driven by the velocity of a particle along S₀ dimension. How fast time appears to pass for a massive particle can be equivalent to the ratio of its S₀ component of velocity μ to the speed limit c as,

$$$$

1 γ*

=

μ c

(4)

Where γ^* is the equivalent Lorentz factor for the S₀ dimension. Since,

μ² = c² – ν²                            (5)

γ^* = $\frac{1}{\sqrt{\mathrm{1-\; <math\; display="block">\; <mrow>\; <mo>(</mo>\; <mfrac\; linethickness="1">\; <mi>v²</mi>\; <mi>c²</mi>\; </mfrac>\; <mo>)</mo>\; </mrow>\; </math>}}}$                        (6)

Speed limit asymmetry

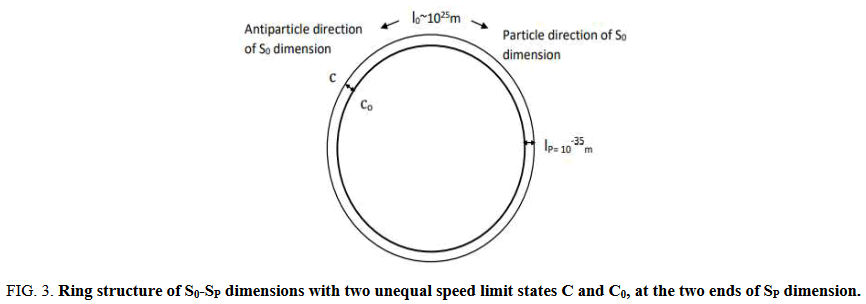
The asymmetry in speed limits c and c₀ is described by the asymmetry parameter Γ which is the ratio of the sizes of S_P and S₀.

Γ =

2πlP lo

~ 10-60

(7)

Where l_o is the size of S₀ and l_P is the Planck length which is also the size of the S_P dimension (Figure 3).

And,

C_o = C[1-Γ]                            (8)

Gravitational state oscillation

Standard model particles oscillates between the two speed states which are also opposite gravitational on and off states. This is such that for a particle of energy E, the state life time t_s for such particle is,

t_s = $\frac{\mathrm{4\pi \hslash }}{\sqrt{\mathrm{<em>E_P</em>²-<em>E_P</em>\; <math\; display="block">\; </math>}}}$                        (9)

Where,

ℏ=Reduced Planck constant.
E_P=Planck en

ergy. The oscillation of standard model particles between the two gravitational states G₀=0G and G₀=2G, makes gravity discrete on microscopic space time scale. It however appears smooth on macroscopic space time scale with an average gravitational constant G.

Energy density constraint

The energy density constraint essentially constrains the total energy density in a given volume of space to always equal the upper limit of the Planck density ρ_P.

ρ_P is only obtainable in the gravitational active state where the speed limit is c while the bare vacuum energy component exists in the inert state with lower speed limit and hence lower Planck density ρ_P0,

ρ_P² = ρ_m² + ρ_vac²                          (10)

Where,

ρ_vac=Vacuum energy density. ρ_m=Total baryonic matter density.

The key significance of this is in the emergence of non-zero Λ dark energy in section 4. However, such energy density constraint implies a Planck density limit to the density of black holes like that suggested in, where Planck stars replaces black hole singularities [14].

General relativity in S₀ dimension

Solution of Einstein’s field equations in 1+1 dimension is being used as a pedagogical tool and reveals some interesting properties of the equations in such dimensionality [15, 16].

In this section, the focus is on general relativity in -1+1 dimension which has some inverted features not seen 1+1 dimensionality because of the negative spatial dimension. The negative dimension number of the S₀ dimension gives it sometime like features such as appearance of positive energy density as negative energy density and the inversion of positive pressure to negative pressure. Einstein’s field equations in S₀ can be expressed as,

G_μν^* + Λ^*g_μν = $\frac{\mathrm{<em>8\pi G</em>}}{\mathrm{<em>c⁴</em>\; <math\; display="block">\; </math>}}$T_μν^*                (11)

Where,

G_μν^*=Equivalent Einstein tensor or the curvature terms in S₀ dimension.
Λ^*=Equivalent cosmological constant. T_μν^*=Stress energy tensor as seen in S₀ dimension.

In -1+1 dimensionality, just as in 1+1, the curvature term G_μν^* is zero, and equation (11) becomes,

Λ^*g_μν = $\frac{\mathrm{<em>8\pi G</em>}}{\mathrm{<em>c⁴</em>\; <math\; display="block">\; </math>}}$T_μν^*                      (12)

Which is essentially a linear algebraic equation and can be further decomposed into a spatial and a time component which is not feasible in 3 +1 dimensionality [16].

Λ^*g_xx = $\frac{\mathrm{<em>8\pi G</em>}}{\mathrm{<em>c⁴</em>\; <math\; display="block">\; </math>}}$T_xx^*                      (13)

Λ^*g_tt = $\frac{\mathrm{<em>8\pi G</em>}}{\mathrm{<em>c⁴</em>\; <math\; display="block">\; </math>}}$T_tt^*                         (14)

Features of general relativity in S₀ dimension

The negative one dimensionality of S₀ confers on it some unique features such as:

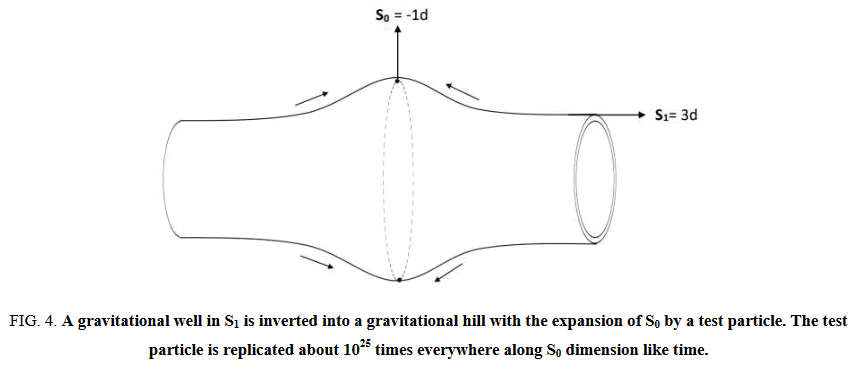
Energy in S₁=Energy everywhere in S₀: An energy density associated with a given Planck volume of 3d space S₁ appears as an equivalent energy density everywhere along S₀ dimension associated with it as illustrated in Figure 4. This makes any form of energy density and positive pressure in S₁ appears as a cosmological constant in S₀.

Positive energy density in S₁=Negative energy density in S₀: Due to the negative dimensionality, any positive energy density in S₁ is inverted and appears as negative energy density which drives the positive cosmological constant expansion of S₀.

Positive pressure in S₁=Negative pressure in S₀: Any form of positive pressure in S₁ appears as negative pressure in S₀ for the same reason of negative dimensionality. The result is a positive cosmological constant expansion of S₀.

Negative pressure in S₁=Positive pressure in S₀: The same negative dimensionality causes the inversion of negative pressure in S₁ appearing as positive pressure in S₀ driving its negative cosmological constant contraction.

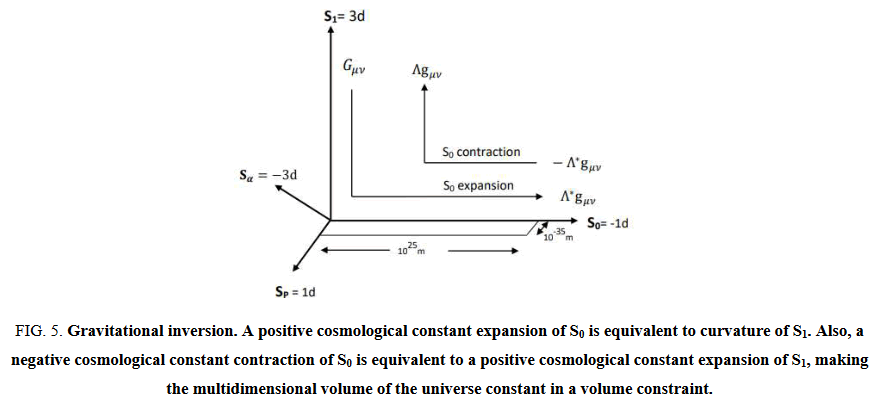
Curvature term G_μν in S₁= Λ*g_μν in S₀: The inversion of roles also results in the curvature term in S₁ being equivalent to positive cosmological constant expansion S₀ as illustrated in Figure 5 and equation (15).

Positive cosmological constant (+Λ) in S₁= −Λ*g_μν in S₀: A positive cosmological constant in S₁ is equivalent to a negative cosmological constant in S₀ as illustrated in Figure 5 and equation (16).

G_μν + Λ^*g_μν = 0                          (15)

Λg_μν – Λ^*g_μν = 0                          (16)

Gravitational chain of causality

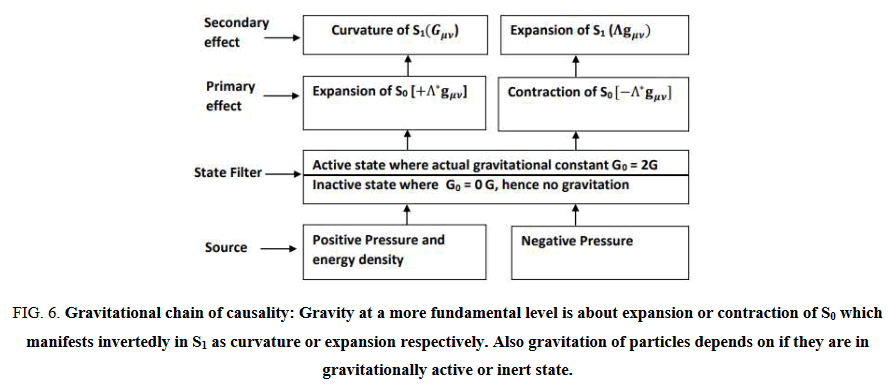
The inversion of gravitation discussed in the previous section suggests that fundamentally, gravity is the expansion or contraction of S₀ dimension. This then manifests in an inverted form as curvature or expansion of S₁ dimension as illustrated in Figure 5.

The existence of gravitational on and off states acts as a filter in this gravitational chain of causality enabling real particles to gravitate while virtual particles are inert (Figure 6).

The relatively permanent existence of the bare vacuum energy component in the gravitationally inert state ensures that it does not gravitate. This partly solves the cosmological constant problem. The second part of the problem about the non-zero value is addressed in the next section.

Emergence of non-zero cosmological constant

The asymmetry in speed limit described in equation (8) between the two gravitational states also reflects in the values of their Planck densities such that,

ρ_P0² = ρ_P² [1-Γ⁴]                          (17)

Where;

0 =Lower Planck density in C0 state and is the Planck density in the C state. The existence of the bare vacuum energy component in the lower C0 state implies that,

ρ_νac = ρ_P0                                        (18)

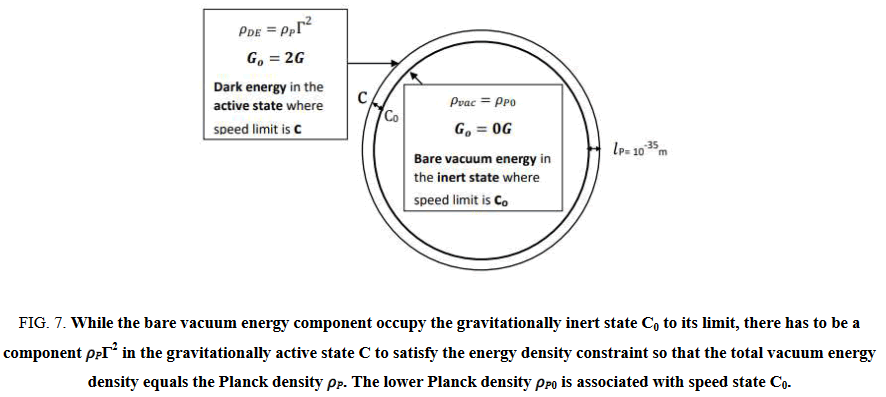
Which is less than the Planck density and the energy density constraint requires that the total vacuum energy density should be equal to the Planck density in the absence of matter.

Since the gravitationally inert lower speed state lacks the capacity to contain all the vacuum energy components, a small component spills into the gravitationally active state as dark energy (Figure 7).

ρ_DE = ρ_PΓ²                                        (19)

And since Γ is suppressed with the expansion of S₀ in the gravitational well of massive objects (equation (7) the density of this form of dark energy varies spatially according to this suppression (Figure 4). The deeper the gravitational well the more the suppression. And substituting the value of Γ from equation (7),

ρ_DE = $\frac{\mathrm{<em>4\pi ²\rho _P</em>}}{\mathrm{<em>l₀</em>²\; <math\; display="block">\; </math>}}$                                           (20)

Where l₀ is the size of S₀ dimension in Planck unit, which increases with the absolute value of the gravitational potential Φ.

Gravitational Wave Reheating (GWR) prediction

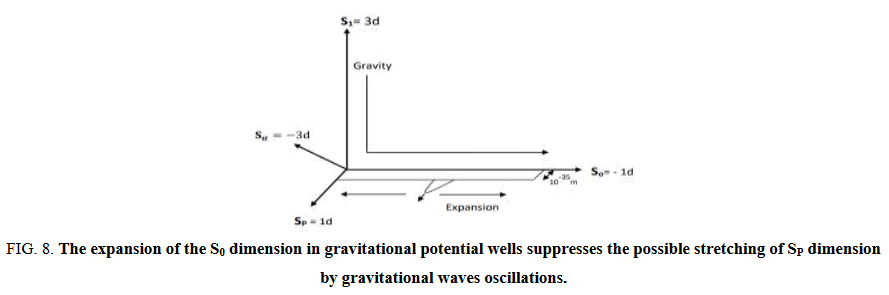
The propagation of gravitational waves along the visible 3d space S₁ should naturally vibrate any extra spatial dimension such as the S_P and S₀ dimensions. Stretching of S_P dimension during such vibration will cause a squeeze out of vacuum energy as photons. This is the Gravitational Wave Reheating (GWR) mechanism of Rute. However as illustrated in Figure 7, the expansion of S₀ dimension in gravitational wells suppresses the possible stretching of S_P dimension resulting in threshold value of strain h and frequency f_g below which reheating cannot occur (Figure 8).

If the S_P dimension stretches, it will reduce the value of the Planck density and the energy density constraint will squeeze out a component of vacuum energy as standard model photons.

Results and Discussion

Energy scale of reheat photons

The maximum energy of the reheat photons that can be emitted in the resulting spectrum can be described by,

E_max = h₀E_P                                        (21)

Where,

E_P=Planck energy.
h₀=Effective strain for the S_P dimension. And,

h₀ = $\frac{\mathrm{<em>hf_g\; –\; H₀^*</em>}}{\mathrm{<em>f_g</em>\; <math\; display="block">\; </math>}}$                                           (22)

Where,

f_g=Gravitational wave frequency.
h=Strain and both represent the threshold that has to be exceeded for reheating to occur.
H₀*=Equivalent Hubble constant associated with each cubic Planck volume describing the expansion rate of S₀ dimension.
H₀*=Proportional to the curvature of the visible 3d spatial dimension S₁ and hardens the S_P dimesions against gravitational wave
vibration.

Magnetic softening of the S_P dimension

The magneto curvature coupling aspect of general relativity was explored based on its tendency to flatten curvature and even dampen gravitational waves [17]. The key aspects of this coupling, is the vector nature of the magnetic field and the magnetic tension that tends to straighten the field lines against distortion by curved space time background.

Essentially the distortion of the field lines by curved background or a passing gravitational wave causes a back reaction from such magnetic field, flattening the curvature or ripples in the fabric of space time. This dampens the gravitational wave amplitude and energy, and can be seen as the hardening of the visible spatial dimensions against gravitational oscillation.

Within the Rute framework, the expansion rate H₀* of the S₀ dimension is a measure of spatial curvature. Therefore the flattening of space time curvature suppresses H₀* in equation (22), resulting in the softening of S_P dimension which becomes more sensitive to gravitational wave oscillation. Indeed with a flat geometry which implies H₀*=0, equation (22) becomes,

h₀ = h                                                   (23)

Where the strain h₀ of S_P vibration becomes equal to the strain h of the incident gravitational wave resulting in maximum reheating. In essence, a strong magnetic field like that obtainable around magentas softens the S_P dimension by lowering the threshold strain and frequency required for reheating to occur for incident gravitational waves.

Strictly from energy conservation perspective, the energy lost by gravitational waves passing through a strongly magnetized region has to be released in some form and Rute’s GWR provides the mechanism for converting the gravitational wave energy into electromagnetic one. It is expected that the brief burst of electromagnetic waves radiated while the gravitational wave passes through a strongly magnetized region such as magentas, encodes information about the incident gravitational waves. These burst of electromagnetic radiation can appear as Fast Radio Burst (FRBs) or even Gamma Ray Burst (GRBs) depending on source proximity or strain and frequency of the incident gravitational waves, making magnetars possible astrophysical gravitational wave detectors.

Dark matter from vacuum energy

The bare vacuum energy component should always be gravitationally inert with its existence in the G₀=0G state where the gravitational field is effectively switched off. However, in this framework, particle substrates of the standard model such as neutrinos affects their background while in the inert state such that G₀>0G.

Within such background in the inert state, neutrinos provides some gravitational illumination described by equation (24) that enables virtual particles to gravitate with positive pressure appearing as dark matter.

G_ν = βΓ²G                                             (24)

Where,

G_ν=Induced gravitational constant in the inert state due to the background effect of neutrino substrates.

β=Dimensionless free parameter and the value varies with neutrino flavor and energy. It varies from 1 and approaches infinity as neutrino speed approaches speed limit c. Γ is the same asymmetry parameter involved in the emergence of dark energy.

With the expression of Γ in equation (7), equation (24) becomes,

Where l₀ is the size of the S₀ dimension (in Planck unit) which is proportional to the absolute value of the gravitational potential Φ and suppresses this substrate effect of neutrinos and hence the near absence of dark matter effect in deep gravitational potential wells.

The value of G_ν falls off quickly within the range of the weak interaction indicating a possible link between the value of G and the weak interaction.

While hot dark matter is the form of dark matter that can be produced by relativistic neutrinos, cosmic neutrinos are unrelativistic. Such non relativistic cosmic neutrino substrates should be further slowed down by the Higgs like drag from its self-induced gravitational interaction with virtual particles within its background. This enhances the clustering of cosmic neutrino substrates and the gravitating virtual particles in their background appear as cold dark matter.

The potential suppression of G_ν enables this substrate dependent form of dark matter to have hybrid behavior by mimicking modified gravity form of dark matter such as Modified Newtonian Dynamics (MOND) while also exhibiting some particle behavior of its neutrino substrates like the superfluid dark matter described in [18]. The details of its unique properties will be discussed in subsequent papers [19-21].

Conclusion

Rute provides an elegant framework for the resolution of the cosmological constant problem of dark energy and the nature of dark matter. In doing so it provides a deeper insight into the dimensional structure of space time and chain of causality involved in gravitation. Specifically, it places the bare vacuum energy component in a state where the gravitational field is switched off with actual gravitational constant G₀=0G, while real standard model particles oscillate between this gravitationally inert state and the active state.

Due to an energy density constraint and a speed limit asymmetry that limits the capacity of the inert state to contain the entire vacuum energy component, a small component spills into the active state as dark energy. The asymmetry parameter emerges from a key dimensional symmetry and it is the ratio of the size of the spatial equivalent of time S₀ and its microscopic partner S_P.

The illuminating effect of neutrino substrates particularly cosmic neutrinos, induces non zero gravitational constant in the inert state, providing gravitation for virtual particles which appears as dark matter. This baryonic substrate dependent form of dark matter can exhibit hybrid characteristics of particle dark matter and modified gravity form of dark matter like superfluid dark matter. It also indicates a possible link between the value of G and the weak interaction.

The reheating prediction in which gravitational waves produce electromagnetic secondary’s with negative pressure from strong magnetic fields of magnetars and dark energy might be the sources of Fast Radio Bursts (FRBs) and Excess Radio Background (ERB).

In conclusion, the Rute framework offers new physics explanations for dark energy and dark matter as different manifestations of vacuum energy that can be tested and provides deep insights into the dimensional structure of space time and gravity.

References

1. Riess AG, Filippenko AV, Challis P, et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron J. 1998;116(3):1009.

   [Google Scholar]

2. Perlmutter S, Aldering G, Goldhaber G, et al. Measurements of Ω and Λ from 42 high redshift supernovae. Astron J. 1999;517(2):565.

   [Crossref] [Google Scholar]

3. Ade PA, Aghanim N, Arnaud M, et al. Planck 2015 results-xiii. Cosmological parameters. Astron Astrophys. 2016;594:A13.

   [Crossref][ Google Scholar]

4. Carroll SM. The cosmological constant. Living Rev Relativ. 2001;4(1):1-56.

   [Crossref] [Google Scholar] [PubMed]

5. Kachru S, Kallosh R, Linde A, et al. De Sitter vacua in string theory. Phys Rev D. 2003;68(4):046005.

   [Crossref] [Google Scholar]

6. Banks T, Dine M, Motl L. On anthropic solutions of the cosmological constant problem. J High Energy Phys. 2001;2001(01):031.

   [Crossref] [Google Scholar]

7. Arkani-Hamed N, Dimopoulos S, Kaloper N, et al. A small cosmological constant from a large extra dimension. Phys Lett B. 2000;480(1-2):193-199.

   [Crossref] [Google Scholar]

8. Kachru S, Schulz M, Silverstein E. Self-tuning flat domain walls in 5d gravity and string theory. Phys Rev D. 2000;62(4):045021.

   [Crossref] [Google Scholar]

9. Copeland EJ, Sami M, Tsujikawa S. Dynamics of dark energy. Int J Mod Phys D. 2006;15(11):1753-1935.

   [Crossref] [Google Scholar]

10. Huterer D, Shafer DL. Dark energy two decades after: Observables, probes, consistency tests. Rep Prog Phys. 2017;81(1):016901.

    [Crossref] [Google Scholar] [PubMed]

11. Oks E. Brief review of recent advances in understanding dark matter and dark energy. New Astron Rev. 2021;93:101632.

    [Crossref] [Google Scholar]

12. Arun K, Gudennavar SB, Sivaram C. Dark matter, dark energy, and alternate models: A review Adv Space Res. 2017;60(1):166-186.

    [Crossref] [Google Scholar]

13. Umar KA, Ayatunji BG, Chizea FD, Nature of Dark Energy, SSRG Int J App Phys. 2019;6(3);1-8.

    [Crossref] [Google Scholar] [PubMed]

14. Rovelli C, Vidotto F. Planck stars. Int J Mod Phys D. 2014;23(12):1442026.

    [Crossref] [Google Scholar]

15. Boozer AD. General relativity in (1+1) dimensions. Eur J Phys. 2008;29(2):319.

    [Crossref] [Google Scholar]

16. Mellinger Jr RD, Weber F, Spinella W, et al. Quark deconfinement in rotating neutron stars. Universe. 2017;3(1):5.

    [Crossref] [Google Scholar]

17. Tsagas CG. Magnetic tension and the geometry of the universe. Phys Rev Lett. 2001;86(24):5421.

    [Crossref] [Google Scholar] [PubMed]

18. Hossenfelder S, Mistele T. The Milky way’s rotation curve with superfluid dark matter. Mon Not R Astron Soc. 2020;498(3):3484-3491.

    [Crossref] [Google Scholar]

19. Zhang B. The physics of fast radio bursts. arXiv preprint arXiv:2212.03972. 2022.

    [Crossref] [Google Scholar]

20. Petroff E, Hessels JW, Lorimer DR. Fast radio bursts at the dawn of the 2020's. Astron Astrophys Rev. 2022;30(1):2.

    [Crossref] [Google Scholar]

21. Fialkov A, Barkana R. Signature of excess radio background in the 21 cm global signal and power spectrum. Mon Not R. Astron. Soc. 2019;486(2):1763-1773.

    [Crossref] [Google Scholar]