Research

, Volume: 13( 2) DOI: 10.37532/2320-6756.2025.13(2).404

• View PDF
• Download PDF

Shape and Size of the Universe

Subhajit Waugh*

Department of Atomic Energy, Theoretical and Computational Physics Section (TCPS), Raja Ramanna Centre for Advanced Technology (RRCAT), Indore, Madhya Pradesh, India

*Correspondence:

Subhajit Waugh
Department of Atomic Energy, Theoretical and Computational Physics Section (TCPS), Raja Ramanna Centre for Advanced Technology (RRCAT), Indore, Madhya Pradesh, Indian
E-mail: subhajit_waugh@rrcat.gov.in

Received: April 08, 2024, Manuscript No. TSPA-24-131837; Editor assigned: April 13, 2024, PreQC No. TSPA-24-131837 (PQ); Reviewed: April 28, 2024, QC No. TSPA-24-131837;Revised: March 07, 2025, Manuscript No. TSPA-24-131837 (R); Published: March 14, 2025, DOI. 10.37532/2320-6756.2025.13(2). 404.

Citation: Waugh S. Shape and Size of the Universe. J Phys Astron. 2025; 13(2). 404.

Abstract

The standard model of cosmology is based on the Friedmann equations, which are derived from Einstein's field equations of gravity for the Friedmann-Lemaitre-Robertson-Walker (FLRW) metric. The Minkowski Space-Time (MST) metric, which can explain all aspects of special relativity (including time dilation, length contraction, and relative simultaneity), describes space-time far from massive objects. This article contends that the currently accepted mathematical interpretation of the MST metric (as well as the FLRW metric) is incorrect, preventing cosmologists from deriving the correct shape and size of the universe. The temporal parts of both metrics are identical and either metric can be used to determine the shape and size of the universe if the mathematical interpretation is corrected. Our universe is like the 3D hypersurface of a 4D hypersphere. Taking the radial expansion velocity of the universe as c (as dictated by space-time equations) and the age of the universe as 13.8 billion years, the value of the Hubble constant obtained using this model (71.002 km/s/Mpc) agrees well with the accepted values (69.8 and 74 km/s/Mpc calculated by two different methods). The MST metric and Hubble’s law both say the same thing, which demonstrates that the model presented is correct.

Keywords

Shape of universe; Size of universe; Structure of universe; Geometry of universe

Introduction

A recent study by Melia [1] called into question the Standard Model of Cosmology (SMC) in eight different respects and clarified its serious shortcomings. The author claims that a complete revision of the standard model of cosmology is needed. He also claims that each of these points is serious on its own. When taken together, even the most ardent supporter of the standard model of cosmology must agree that it is time for a complete paradigm shift, as many scientists have argued. Kroupa [2] claims that the properties of dwarf galaxies exhibit several irregularities, in particular a strongly anisotropic spatial distribution and strong correlations between acceleration and mass discrepancies. Any model of the universe that invokes dark matter cannot explain these types of irregularities. As the dark matter premise is essential to the SMC, this issue poses a major problem for the SMC. Kroupa [3] also states that the major issues with inflationary Big Bang (BB) cosmologies remain unsolved, which again is problematic for the SMC (which cannot do without cosmic inflation).

The SMC is like a patchwork dress stitched together from diverse ideas and tailored to fit an astonishing number of different observations. Consequently, it is more of a placeholder than a coherent model. Some experts have even asked, “Do we have a standard model of cosmology?” [4]. Several authors have noted problems that this model faces [5].

Melia is not the first scholar to challenge the standard model of cosmology [1]. In fact, Melia et al. [6-8] developed a new model of the universe, called the R_h=ct universe. As already shown by Melia [9], the radius of the Hubble sphere coincides with the gravitational horizon radius (R_h). Melia’s R_h=ct is a constant expansion rate model of the universe (as opposed to the accelerating model of the universe in the SMC, which is also known as the Lambda-Cold Dark Matter (ΛCDM) model or the Concordance Model).

The model presented in this article is a special case of the R_h=ct universe mentioned above. However, it is much more refined and restricted. More importantly, it is based on the correct interpretation of the crucial equations of space time (rather than based on assumptions). The model proposed in this paper shows that the true radius of the universe (RUniv.) always remains equal to the Hubble radius, because the speed of light (which determines the value of the Hubble radius) always remains equal to the radial expansion velocity of our hyper-balloon universe. This article shows that the speed of light (as well as the speed of gravitational waves) is fixed at the particular value c (which is actually the radial expansion rate of the universe) due to the peculiarity of the MST structure.

The model presented in this manuscript can inherit the successes of the R_h=ct universe. Therefore, it may be advisable to mention them. Wie et al. showed that in a pairwise comparison, the probability of the R_h=ct model being correct is 90%, compared to only 10% for a minimalist form of the ΛCDM model, in which dark energy is simply a cosmological constant [10]. Compared to the R_h=ct model, versions of the standard model with more elaborate parameterizations of the dark energy are even less likely. Wu et al. claimed that based on the Gamma-Ray Bursts (GRB) Hubble diagram, the probability that R_h=ct is closer to the correct model is approximately 85%-96%, compared to approximately 4%-15% for the ΛCDM model [11]. Melia claimed that the evolutionary growth of primordial galaxies is consistent with the current view of the formation of the first stars, but only with the timeline provided by the Rh=ct cosmology [12]. A similar view is presented in [13], which claims that high-z quasars may be difficult to explain within the framework of the standard model. Instead, they can be naturally interpreted in the context of the R_h=ct universe. (It should be noted that data from the James Webb Space Telescope have already made the situation extremely uncomfortable for SMC. The situation may only become worse as more data are collected.)

The R_h=ct universe has provoked fierce debate and intense opposition. Regarding the extremely negative criticisms levied against it, Melia [14] states that one-on-one comparative tests between the R_h=ct and ΛCDM models have been performed using over 14 different cosmological measurements and observations. In each case, the data favored R_h=ct over the standard model, with model selection tools yielding a probability of approximately 90%-95% that the former is correct, versus only approximately 5%-10% that the latter is correct. In other words, the standard model without the equation of state (EOS) p=−ρ/3 does not appear to be the optimal description of nature. However, despite these successes or perhaps because of them some concerns about the fundamental basis of the theory itself have been published recently. (Melia demonstrated in another paper that the Friedmann-Lemaitre-Robertson-Walker (FLRW) metric is compatible only with the EOS p=−ρ/3 model.)

Several alternative models of the universe have been proposed. One study [15] provides a non-exhaustive list of these models. The sheer number of alternate models is a testament to the myriad shortcomings of the SMC.

The model presented in this article shows that our 3D space is embedded in a 4D hyperspace. Several authors have speculated for various reasons that our universe may be embedded as a thin membrane in a large dimensional hyperspace. However, most of these models have been wrong about the number of dimensions actually needed (due to a misunderstanding of imaginary numbers) and assumed that at least five dimensions are necessary. Some such models are as follows.

Gogberashvili considered the universe as a bubble expanding in a five-dimensional spacetime [16]. This model is supported by at least two observable facts. First, each galaxy is moving away from all other galaxies, according to Hubble’s law, which is easily explained by the expansion of a bubble universe. Second, there is a preferred frame in the universe from which the Cosmic Microwave Background (CMB) is isotropic. Rubakov et al. [17] discussed the possibility of solving the cosmological constant problem by increasing the number of spatial dimensions (which creates an embedment). Van de Bruck et al. [18] provided a brief overview of the brane world idea, according to which the standard model particles are confined on a hypersurface, which is embedded in a higher-dimensional spacetime (called the bulk). Some other examples of brane world (embeddings of 3D space) are provided in the above-mentioned alternative models of the universe paper. The brane idea is also supported by the fact that both gravity waves and electromagnetic waves (both of which can travel through what we call “empty space”) are transverse rather than longitudinal waves. Transverse waves are generally associated with a string or a membrane/sheet embedded in a higher dimensional space.

The model presented in this manuscript is the hyper-balloon model of the universe. Since the discovery of Hubble’s law, scientists have speculated that the analogy of an expanding balloon best describes the shape of our universe. This view gradually became less popular, although it is still mostly used for educational purposes (but not presented in any serious scientific research). Xu et al. [19] draw an analogy between the expansion of a spherical balloon surface (representing 3D space) and cosmic expansion. It examines the meaning of Hubble’s law and the variation of Hubble’s constant with time. They also examine the motion of objects moving on the surface of this balloon and conclude that an expanding balloon is a good metaphor for the expansion of the universe. The expanding balloon model is also used as a metaphor for an expanding spacetime by Zendri et al. [20].

The expanding balloon model was gradually ignored and replaced by the currently accepted model of a flat and infinite universe, which is shown in this study to be based on false assumptions.

An analysis of CMB spectra using Planck satellite data now favors a positive curvature of our universe (rather than flat) with a confidence level greater than 99%. It also argues for a closed universe, which can naturally explain the anomalous lensing amplitude and removes a well-known tension in the Planck dataset. In short, Planck power spectra favor a closed universe. A cosmological crisis is being masked under the assumption of a flat universe.

The Planck 2018 studies have received Bayesian betting odds of over 2000?1 against an open universe and over 50?1 against a flat universe, which has serious negative implications for the SMC.

The analysis of astronomical data suggests that the universe is finite. It should also be noted that at least two solid scientific arguments strongly favor a finite universe. The first relates to a thought experiment developed by Newton with two buckets partially filled with water, which demonstrated that inertia must involve a frame of reference in which distant stars and galaxies are at rest. Later, Mach concluded that the amount of inertia felt by a body must be proportional to the total amount of matter in the universe. Thus, an infinite universe would guarantee infinite inertia and make it impossible for things to move. Second, the probability of an infinite universe being created must be zero because the energy required is infinite, and no quantum fluctuation can muster such a sum.

The CMB power spectrum on large angular scales (for regions typically more than 60° apart) shows a strange power loss. The standard model of cosmology cannot explain this feature. If space is infinite and flat (as currently believed), then the waves created at the BB would fill the cosmos at all length scales. A loss of power beyond 60° means that the broadest waves are not present, which indicates that space itself is not large enough to support these waves.

All this evidence suggests that astronomers are wrong about the shape and size of the universe. A major obstacle to deciphering the true shape and size of the universe has been the incorrect mathematical interpretation of the spacetime equations (both the Minkowski and FLRW metrics) and in particular, the incorrect mathematical interpretation of the relative simultaneity implied by these metrics. The concept of the block universe (introduced by Einstein and Minkowski), in which there is no distinction between past, present and future, which all exist simultaneously, is due to faulty understanding of relative simultaneity. Scientists have mistakenly used the analogy of a loaf of bread that can be sliced at different angles. The logic is that when observers are in motion, then the spacetime loaf would be cut at an angle, which means that the “now” of one observer would be significantly different from that of another. Each observer will have their own plane of simultaneity. Observers moving at different relative velocities have different planes of simultaneity. This loaf of bread analogy leads to the Rietdijk–Putnam paradox (Andromeda paradox), which does not support this viewpoint, but only exposes it as ridiculous.

A much more appropriate analogy would be the printer cartridge analogy. Although the cartridge can only move back and forth on a 1D metal rod, it can still print any slanted line (at any angle of inclination) on 2D paper because the paper moves. The same is true if the 2D paper is held still and the metal rod moves up (or down) while the cartridge moves sideways.

An extremely important study by Dirac concerning the future of cosmology has largely been ignored by cosmologists. Dirac demonstrates that there is a preferred time-axis and an absolute time in cosmology. This situation deviates strongly from the principles of relativity (both special and general) and thus, he strongly asserted that relativity would play only a minor role in the field of cosmology. Unfortunately, the currently accepted model of cosmology is based solely on general relativity (without understanding the true meaning of spacetime itself) without considering the other pillar of physics, quantum mechanics, which many physicists consider even more fundamental. The model presented in this study is fully compatible with both quantum mechanics and relativity (in fact, both arise naturally from this model), as space and time exchange roles on a tiny size scale, causing the transition from the subluminal realm (the classical world of GR) to the superluminal realm (quantum mechanics). However, those concepts require a separate study; therefore, they are not addressed in this article. Dirac’s paper also points out that the radiation pressure in the universe is negligible and hence that Friedmann’s assumption of a cosmic fluid in which mass density and radiation pressure are both major players needs to be seriously re-examined.

The rest of this paper is organized as follows. In section 2, the correct representation of negative and imaginary numbers is discussed. It is shown that our improper understanding of those concepts has led to a wrong mathematical interpretation of spacetime itself. Rectification of that mistake leads us to deduce the true shape and size of our universe. To gain confidence in the model here presented of the universe, the mathematical calculations are checked. In section 3, objections against this model are addressed individually and found to fail. It is shown that our universe is not infinite in extent, but rather is much smaller. Even the size of our observable universe is found to have been overestimated. The consequences of the presented model (like rest-mass momentum, which can simplify and unify physics) are discussed. Finally, in section 4, the extremely problematic BB singularity is addressed and this model is found to overcome that previously insurmountable problem as well.

Materials and Methods

Space-time is the arena where everything occurs and the fabric that comprises the universe. Therefore, an accurate picture of space time is crucial to unraveling the shape and size of the universe

The Minkowski-Einstein space-time equation

ds²=(icdt)²+dx²+dy²+dz²=(icdt)²+dr² (1)

which explains all of special relativity, including time dilation, length contraction and relative simultaneity, is not a statement about a 4D space-time continuum (because imaginary numbers i cannot be used as an independent axis, as will be shown in the next paragraphs). The manner in which imaginary numbers are represented in the standard Argand diagram (taught in schools worldwide) is incorrect. One must correct the way negative numbers and imaginary numbers are represented.

Correct representation of negative and imaginary numbers

Imaginary numbers are ubiquitous in quantum mechanics and spacetime physics. The imaginary number i enters through the temporal dimension and makes the spacetime metric (–, +, +, +) instead of (+, +, +, +). Although mathematicians correctly identified that i (the square root of –1) represents a rotation of 90°, scientists did not recognize that the imaginary sign (i) must disappear if a perpendicular axis (additional dimension) is explicitly used. The imaginary sign i can remain only as long as one does not use an additional axis. This assertion can be justified by the following example: suppose that Mr. XYZ borrowed $1000 from the bank and spent it. Then one can either say that “Mr. XYZ has a debt of $1000” or “Mr. XYZ owns –$1000.” However, one must not say that “Mr. XYZ has a debt of –$1000.” The negative sign automatically indicates the direction (because debt goes in the opposite direction of ownership). Therefore, if negative numbers are used (i.e., along with the minus sign), then one should use the positive x-axis (i.e., in the same direction as the positive numbers). If one does not use the minus sign, then one should use the negative x-axis (in the opposite direction to the positive x-axis from the selected origin). However, one should never use both together. A similar argument applies to the imaginary number i (Figure 1).

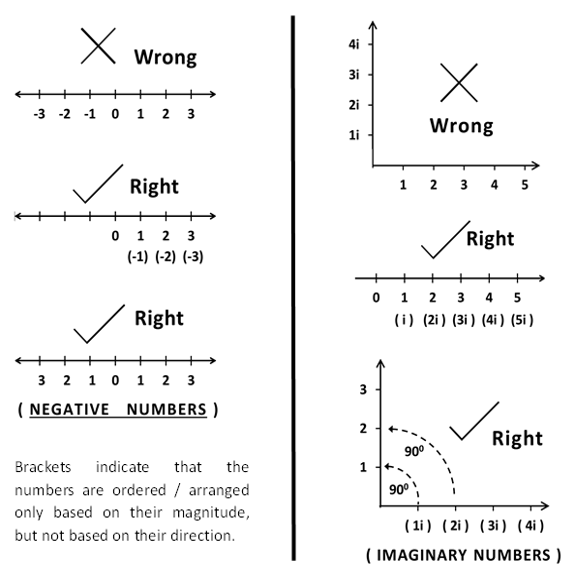
FIG. 1. Correct representations of negative and imaginary numbers.

It is likely that we make the (above-mentioned) grave but unnoticed mistake because we obsessively want to arrange the numbers (based on their magnitude) on the number line (e.g., the x-axis). Suppose that we begin with 2 and compare it to 1. Because 1 is less than 2, we place it to the left of 2. We then compare 1 to 0 and place 0 to the left of 1. Next, we compare 0 and –1, find that –1 is less than 0, and place –1 to the left of 0.

In doing so, we conveniently forget the important fact that we have the origin at 0. On the positive x-axis, placing any number to the left brings us closer to origin. However, on the negative x-axis, placing it to the left takes it away from the origin. The rule has reversed.

While we were using positive numbers (such as 2, 3 and 12) for ordering, we followed the rule that smaller numbers are closer to the origin and larger numbers are farther away. However, when arranging negative numbers (in the conventional way), we follow the rule that larger numbers are closer to the origin and smaller numbers are farther away.

Therefore, such an arrangement works only if there is no origin on the number line. Such a number line may be of interest to mathematicians (as a fancy ordering tool), but we do not need it for physics. In nature, the origin is definitely at 0 (it is the terminus). Nature does not use negative numbers (or even imaginary numbers). They only occur in our mathematical descriptions of physical laws. Negative/imaginary numbers are only mathematical tools. They do not exist in nature. How can I have –4 cows? (Here –4 is meant quite literally, raising the question, “What does a negative cow look like?”). This situation is exactly why mathematicians were once so reluctant to accept negative and imaginary numbers. They are not physical. In addition, of course we need an origin when working with dimensions. Certainly, we need an intersection (crossing) point between the X- and Y-axes (or even the Z-axis). It is difficult to imagine how a number line without an origin can be used to create a XYZ frame ofreference.

The attentive reader will have noted a difficulty. Even using the positive X-axis to arrange negative numbers (as shown in the figure), we still encounter the difficulties that whereas the positive numbers follow the rule that smaller numbers are closer to the origin and larger numbers are farther away, the rule is reversed for the negative numbers. That is exactly why the negative numbers are shown in brackets in the diagram. We cannot order the negative numbers similarly to the positive numbers on the positive x-axis. However, this problem disappears completely when we can represent negative numbers as positive numbers in the direction of the negative x-axis. In other words, this problem disappears with access to the opposite direction. The above-mentioned problem becomes even more pronounced when we move to imaginary numbers because i=sqrt (–1) is not less than 0, greater than 0 or equal to 0. Imaginary numbers cannot even be arranged by comparing their magnitudes (because we lose the property of ordering altogether with imaginary numbers). However, if we have access to another perpendicular axis (in this case, fortunately, the y-axis), then i=1.i represents the (real) number 1 on the y-axis. Again the (above-mentioned) problem disappears if we have access to a higher dimension (i.e., perpendicular axis). Therefore, the emphasis is not on where on the x-axis the imaginary numbers should be placed (they are just a mathematical convenience anyway), but rather on the fact that they represent a real quantity on a very real axis.

“Why then should we not use an additional axis instead of resorting to imaginary numbers?” This is certainly a good question. If the x-axis is not sufficient, then we can add the y-axis. If we need another dimension, we can use the z-axis. Then we are stuck. We cannot go any farther. However, the shocking aspect is that we most certainly need another dimension that we do not have access to. We are flatlanders. The need for a fourth dimension was recognized by Einstein and Minkowski (although they missed the actual picture and created problem with a block universe view).

The assumption of a 4D space-time continuum leads to a block universe where there is no distinction between the present, the past and the future. Minkowski and Einstein made this mistake. Our daily experience, as well as numerous scientific observations, are in stark contrast to the block universe view. The number of contradictions is so great that an entire book has been written to illuminate this glaring error.

The true meaning of Minkowski space time

The equation

ds²=(icdt)²+dx²+dy²+dz²=(icdt)²+dr² (2)

represents a dynamic 3D hyper sheet (consisting of fields and particles), which can be referred to as a 3D Field-Particle Hyper Sheet (FPHS) moving with a velocity c in the fourth dimension in an embedding 4D hyperspace. The above statement is easy to prove. Consider an arbitrary observer located somewhere in 3D space and moving at an arbitrary velocity. Relative to itself, the observer is not moving through space (dr=0). Therefore, the above equation (if we set dr=0) becomes

ds²=(icdt)² (3)

Therefore,

ds/dt=i.c (4)

Consequently, every Frame of Reference (FOR) reaches the same conclusion. The presence of i clearly shows that everyone is moving with velocity c in a direction perpendicular to all of the x-, y- and z-axes (which is an impossible direction for any observer trapped in this 3D space. Why is it an impossible direction? Try to point their finger toward the future or the past. This direction is perpendicular to any direction in which he/she can point). Note that the above procedure also applies to any free-falling observer in the FLRW metric (in the presence of a gravitational field) because GR guarantees that the FLRW metric is also locally Minkowskian. An alternate justification can be given that the temporal part of both MST and FLRW metric are identical. One can use only the temporal part to prove that every FOR is moving with a velocity c in the fourth dimension. Therefore, the above conclusion is unavoidable.

The smartest minds of the last century determined that we are all moving through space-time at a velocity c (the speed of light), i.e., we are moving either through space or through time or a combination of the two. However, they failed to draw the correctconclusion that every observer (or frame of reference) is moving at velocity c in a single direction (the fourth dimension)regardless of their location or velocity in the 3D space. We are all moving through the fourth dimension of (hyper) space at 1079million km/h (670.6 million miles/h). However, it is extremely difficult to sense this motion because this direction isperpendicular to all of the x-, y- and z-axes (and therefore an impossible direction for humans). Moreover, everything (includingthe desk, chairs, buildings, gardens and trees) move together, giving no feeling of relative motion.

Any frame of reference can only come to the same conclusion if the entire 3D hypersurface (3D space) is moving in the same direction. That is why emphasis is placed on 3D FPHS (instead of 3D space) in this article. A 3D space moving through a 4D hyperspace makes no sense. Alternatively, a 3D FPHS moving (with velocity c) through 4D hyperspace does make sense.

Therefore, the physical meaning is clear: 3D space is a 3D hypersurface embedded in 4D hyperspace. What does this 3D hypersurface comprise? It consists of fields and particles (which are only resonances in that field). This is just the core statement of the amazingly accurate quantum field theory. Therefore, what we call 3D space turns out to be a 3D FPHS. Laughlin mentioned that particle accelerators have definitely proven that space is more like a solid block of glass than the perfect void that scientists had previously imagined. It is composed of material that is invisible but can be made visible if it is hit sufficiently hard to knock bits out. Therefore, the modern concept of the vacuum of space is, like relativistic ether, confirmed by numerous experiments. However, scientists are afraid to describe it that way because it is taboo. The same view is taken by Sorli and Celan, who claim that the idea of empty space has harmed physics for more than a century and must be banished to reintroduce the ether into physics. (Clearly, Einstein’s logic for banishing ether from physics based on the constancy of the speed of light for every observer is incorrect. That postulate would be satisfied simply if the MST equation holds. As already seen, special relativity and the MST structure are all about being trapped in the dynamic hypersurface (3D FPHS) but free to move along the hypersurface in any three directions. Therefore, special relativity itself tacitly brings ether back into physics. Readers might wonder if Einstein ever considered how electromagnetic waves could travel through an absolute vacuum. Besides, why should an absolute vacuum have measureable physical properties like permittivity and permeability?).

The lack of understanding of i=sqrt (–1) led scientists to conclude that the velocity of the 3D FPHS (ds/dt=i.c) was imaginary, and they were therefore discouraged from digging deeper. They simply found it more convenient to conclude that our space-time is very peculiar (hyperbolic), without questioning why this peculiarity occurs in the first place.

The possibility of a dynamical three-space has been explored by Cahill and was backed up with some solid arguments.

It is not easy to see what a great achievement the concept of a dynamical 3D hypersurface is unless one is intimately conversant with the intense debate that has raged for well over a century about the dimensionality and meaning of space-time and which is far from over. Several papers are sufficient to convince the reader that a non-dynamic space (non-dynamic 3D FPHS) is a mathematical impossibility.

How can everything we observe (including huge boulders, mighty mountains and even our rock-solid planet) be just an extremely thin (hyper) surface? The answer is, it is extremely thin along the fourth dimension and not along the other three dimensions. Regarding the solidity of mountains, quantum mechanics provides the answer. One thing that quantum mechanics has taught us is that the solidity (rigidity) of rocks and the reality of everything we observe is a mere illusion. Niels Bohr famously said, “Everything we call real is made of things that cannot be regarded as real.” Indeed, high-energy particle physics must abandon the idea of a particle in favor of a field. A planet or a star looks like a spherical ball to us. However, to a divine being (God?) who has access to the fourth dimension, it looks like a very thin circular coin embedded in a thin membrane. Even the mightiest mountains are extremely pliable/flexible when viewed from the fourth dimension.

Although we already know that our entire 3D space (which we also call a vacuum) is filled with fields, bursting with energy (in which particles can be created and annihilated spontaneously), we have never figured out that it is this 3D FPHS that makes our geometry 3D. That is because the stars, the planets and even we ourselves are ultimately made up of particles, which are merely resonances/excitations in the 3D hypersurface of fields. Hence, everything we observe is destined to be eternally trapped in 3D FPHS. This is a great trick of nature because the geometry of nature is 4D (i.e., 4D hyperspace). Space (actually, hyperspace) is nothing but a 4D geometry (true vacuum) embedding this 3D FPHS. Imagine a 2D living being that can only move on the surface of a 2D rubber sheet (RS). If the RS is absolutely transparent or invisible and offers no resistance to its motion (unless it changes velocity), the creature will assume that the RS is the space/geometry of the universe itself. It will treat the RS as synonymous with empty space in such a way that it will consider the distance between two visible points on the RS as spatial distance, even if the RS is curved and the line joining the two points happens to be a curved line. Even if it is somehow aware of the existence of the (almost imperceptible) RS, it will ignore its presence and hardly ever take note of the fact that it is a trapped entity. For the purposes of this research, it believed with certainty that this situation is indeed the case.

The simple fact that Einstein mistook this (dynamic) 3D hypersheet for the fabric of spacetime itself becomes very clear when we investigate the 1995 proposal by Jacobson that Einstein’s gravitational equations can be derived from thermodynamics. This concept suggests that gravity is just an average of the behavior of unknown “atoms” of spacetime (rather, not spacetime but the field-particle hypersheet).

The embedding 4D hyperspace is absolute and Euclidean (as it should be) and possibly extends infinitely in all four directions. The void/nothingness may be infinite, whereas our universe (which is shown in the subsequent sections to be shaped like a balloon) is finite and closed. Newton’s concept of absolute space has been restored. Newton would surely be proud. Indeed, we need absolute space to explain both inertia and acceleration. Relativity is all about being trapped inside a dynamic 3D FPHS (but being free to move in any three directions inside the hypersurface), while the 3D FPHS itself is embedded in an absolute 4D hyperspace. This solves the conflict between Newton and Einstein. We need to look out through the window of a moving car to determine whether it is moving or at rest (Einstein’s view), but we can tell with our eyes closed whether the driver has pressed his foot on the accelerator and is therefore accelerating with respect to an absolute space (Newton’s view).

The Minkowski Space-Time Equation (MSTE) can also describe a small section of an expanding (hyper) balloon. In this case, the outward movement (along the radius of the hyper-balloon) of the small section plays the role of the movement along the fourth dimension. The MSTE is a perfect description of an infinitesimally small section on the 3D hypersurface and describes the motion of this point along the fourth spatial dimension. However, it neglects the expansion (stretching) of the hypersurface of the (hyper) balloon that accompanies this motion along the radius of the (hyper) balloon. An analogy to a party balloon makes this situation clearer. As the balloon expands, two things happen simultaneously.

• A point on the wall of the balloon moves away from the true center of the balloon along the radius of the balloon.
• Nearby points appear to move farther away from that point due to the expansion of the wall of the balloon.

A more general treatment is provided by the FLRW metric (instead of the MST metric) that includes a scale factor a(t) that accounts for this spatial stretching. The FLRW metric is

ds²=-c²dτ²=(icdt)²+a(t)²dΣ² (5)

where Σ extends over a 3D space with uniform curvature (this can be an elliptic, Euclidean, or hyperbolic space). It is written as a function of three spatial coordinates, usually in terms of spherical coordinates, but can also be written in Cartesian coordinates. Σ does not depend on time (t). All time dependence is taken care by the function a(t), which is known as the scale factor.

Deducing the true shape and size of the universe

Another major obstacle in determining the true shape and size of the universe is the belief in a flat universe. The concept of a 3D flat universe is the main reason for the introduction of cosmic inflation theory, which has been critiqued in an astonishing number of publications.

Cosmologists are convinced that they have calculated the universe to be (3D) flat by two different methods:

• Summation of plane angles in a triangle method
• Critical mass-energy density method of GR

(The meaning of 3D flat can be understood by an example. The surface of a tabletop and the surface of a sphere (football) are both 2D. However, the surface of a tabletop is flat, whereas the surface of a sphere is curved in the third dimension. A flat surface obeys Euclidean geometry, whereas a curved surface does not. Humans can only imagine three dimensions. However, there is a fourth dimension, as shown by Minkowski. Therefore, 3D space can be considered as a 3D hypersurface in a 4D embedding hyperspace. The 3D hypersurface will be flat if it is not curved in the fourth dimension.)

Unfortunately, neither method can measure the extrinsic curvature of a 3D hypersurface.

The first method relies on checking whether the sum of the plane angles of a triangle formed by two points at opposite ends of a CMB spot (whose size is known) and the point on the measuring instrument is 180° or greater than 180°.

Note: The actual analysis of CMB for testing the flatness of the universe is based on the full 2D pattern of cold and hot spots of the cosmic microwave background decomposed into spherical harmonics, in which the statistical properties of the observed universe are compared with the model predictions. However, it is still based on the summation of the plane angles of a triangle.

Checking the curvature or flatness of a surface by examining whether the sum of the plane angles of a triangle drawn on that surface is 180° or greater works well for a 2D surface that curves in the third dimension (e.g., the surface of a ball). However, when checking the curvature of the universe, one is talking about a 3D hypersurface (i.e., 3D space) that curves in the fourth dimension. What one needs is a tetrahedron, the sum of whose solid angles should be checked. The following is the reason that using the sum of plane angles of a triangle is bound to fail.

Let us go down from a 3D hypersurface to a 2D surface, using the curved surface of the Earth as an example. Suppose that a person starts from point A at the North Pole and moves south to point B on the equator, then moves an equal distance along the equator to point C and turns 90° to face north, then continues their journey to reach point A again. Now each of the angles at A, B, and C is 90°. Therefore, the sum of the angles in the triangle is 270° (Figure 2).

Now they repeat the journey from point A (North Pole) and again reach point B on the equator. However, this time they travel only a few steps and turn 90° again. They continue the journey to reach point A. Now the angles formed at points B and C are both 90°, whereas the angle formed at A is almost 0°. The sum of the angles is now almost 180°.

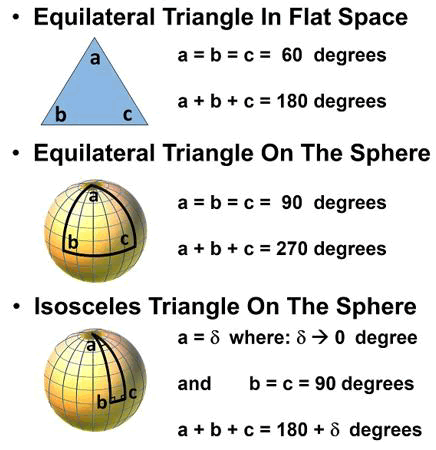
FIG. 2. Triangles on flat and curved surfaces.

Thus, if the triangle shrinks to a line (i.e., point C approaches and eventually merges with point B), it loses its detecting power. One needs a 2D object (like a triangle) and not a 1D object (a line) to measure the curvature of a 2D surface. The same logic applies to a higher dimension. A triangle is nothing more than a tetrahedron with its apex/peak point merged to its base. Therefore, a triangle is useless for measuring the curvature of the universe.

The second method of measuring the curvature of our universe relies on the critical mass-energy density method of GR. However, GR uses the MST metric (although it uses complicated tensor calculus) and thus reflects the viewpoint of a creature trapped inside three dimensions with no access to free motion along the fourth (time) dimension. Both special relativity and GR assume that time itself is the fourth dimension, which is certainly NOT the case, as time does not have the units of meters, feet, yards or miles. Relativity fails to account for the motion of the 3D hyper sheet (which is assumed to be synonymous with 3D space). Time results from motion along the fourth spatial dimension (which makes sense as time has the unit of (Distance (meter))/(Speed (meter/second). There is no concept of “outside” in GR because it is an intrinsic viewpoint (i.e., the viewpoint of a creature trapped in the moving 3D hyper sheet) and consequently GR can measure intrinsic but not extrinsic curvature. The difference between intrinsic and extrinsic geometry is that intrinsic geometry describes curvature without requiring a higher dimension (which is the case with GR), whereas extrinsic geometry requires a higher-dimensional embedding space to describe curvature. This situation is precisely why GR cannot predict the global structure of the universe, nor can it account for the “external field effect,” which has now been confirmed to 11σ accuracy in galaxies. Therefore, GR can be compared to the perspective of a goldfish in a round glass jar. Its viewpoint is not wrong, but it is highly distorted and inferior to that of a human being outside the jar.

Therefore, one cannot be sure that the universe is 3D flat. However, how can one be sure that it is curved? Here is another clue that cuts to the heart of the matter: Our universe has a center, although the center does not lie anywhere in our 3D space (which is actually a 3D hyper sheet composed of fields and particles, i.e., a 3D FPHS). This concept can easily be proven.

The center of mass equation is a powerful equation:

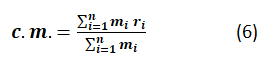
where m_i is the mass of the point particles and r_i are the space coordinates of the point particles.

In the vastness of our cosmos, each galaxy (or a cluster of galaxies) can be considered as a point mass. Even when the number of galaxies (n) tends to infinity (n→∞), there remains a single point as the center of mass. The mere invocation of infinity will not dissuade anyone from the conclusion that there is indeed a center. Further, it must lie outside of the 3D hypersurface. Otherwise, the true center could have been located and Hubble’s law would not have the special form v=H₀D. Also, the BB would not have appeared to have occurred everywhere. In fact, the cosmos would be an irregular structure consisting of an empty central region (the “crater of the explosion”), an intermediate region containing the galaxies, and an external part containing only radiation. No structure in 3D space formed from an explosion 13.8 billion years ago could resemble the universe we observe today.

There is another reason that 3D space (3D FPHS) must be curved. Let us assume that both 3D flat and 3D curved shapes are possible and consider which of the following two models is correct. Two conditions need to be satisfied.

• The 3D hyper sheet moves in a single direction (along the fourth dimension).
• Hubble’s law implies that the entire 3D FPHS is stretched as each galaxy moves away from every other galaxy, althoughthere is no net motion (i.e., motion on average) of galaxies through 3D space.

From the above two conditions, it is easy to derive two different models of the universe:

• An expanding 3D flat universe (an expanding grid model), and
• An expanding 3D curved universe (hyper-balloon universe).

Figure 3 shows three positions of a moving hyper sheet (at various times) in both diagrams. In both cases, the hyper sheet is stretched as it moves upwards (i.e., along the fourth dimension). In the hyper-balloon case, the word “outwards” might be more appropriate than “upwards.” In the first case, it remains 3D flat, whereas in the other case, it resembles a section of an expanding balloon.

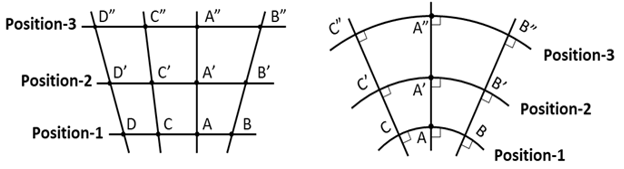
FIG. 3. Comparison between the grid model and balloon model of the universe.

Now, if both conditions are satisfied, then from the first diagram, only one galaxy will move straight upward (and has no sideways movement as the 3D FPHS continues to stretch and move upward). The upward motion here represents the fourth dimension.

In fact, Hubble’s law guarantees that any galaxy lying further than the Hubble distance from galaxy A will be moving sideways at a velocity greater than the velocity of light c.

The equation

ds²=-c² dt²+dx²+dy²+dz² (7)

states that for any galaxy not moving locally, dr=0 satisfies ds=i.c.dt, or,

ds/dt=i.c (8)

This equation clearly states that it only has a velocity of c in the fourth (inaccessible) direction and no lateral velocity component. In the (flat) grid model of the universe, except for galaxy A, all other galaxies violate this equation (because they are inevitably moving sideways as well). The farther the galaxy is from point A, the greater its lateral velocity, which may be far greater than the speed of light at greater distances. The other possibility that remains is a balloon universe, in which all galaxies can simultaneously satisfy both conditions 1 and 2, as well as (8). Therefore, a hyper-balloon best describes the shape of the universe. However, to gain even more confidence, one must verify that the mathematical calculations for the hyper-balloon model are correct.

Verification: Mathematical calculations for the (hyper) balloon universe model

The formula for the circumference of a circle is 2πr (where r is the radius of the circle). Passing from 2D to 3D, the equivalent figure for a circle becomes the spherical surface of a sphere. If a great circle is drawn on the spherical surface (e.g., an equatorial line), the circumference of the great circle is still 2πr.

Moving from 3D to 4D, the equivalent figure for a sphere becomes a hypersphere and thus, the equivalent figure for the spherical surface becomes the spherical hypersurface. However, the formula for the circumference of a (hyper) great circle should remain 2πr. Note that the (hyper) great circle, or HGC, would be drawn on the 3D hypersurface of the 4D hypersphere.

We have assumed a (hyper) balloon model of the universe whose radius is constantly increasing at the speed of light (c). Taking the age of the universe to be 13.8 billion years, the radius of this model of the universe is 13.8 billion light years (distance=velocity (c) × time).

On the basis of the above model, the expansion rate of 3D hypersurface, which we call “our universe” can be easily calculated. At time t1, let the radius of this hypersurface be r. At later time t₂, let the radius of this hypersurface be equal to R. The circumference of the HGC drawn on this hypersurface increases at a rate given by

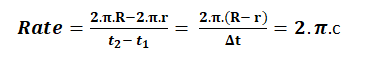
assuming the limit Δt→0.

The total circumference of this (hyper) great circle is 2πR (or 2πr, whose difference from the former does not matter if we take the limit Δt→0). To calculate the rate of expansion of this HGC per unit distance of the HGC, we should take the ratio (K₀)=2πc/2πR=c/R, where R=13.8 billion light years = 13.8 × 10⁹ × (365 × 24 × 60 × 60) × c.

(Taking the value of c as 2.99792458×10⁸ ms^-1, the value of radius of the universe (R) is approximately 1.3047 × 10²⁶ m, which is approximately the same as the value of R_univ.=1.28 × 1026 m given by Mercier as the apparent curving radius (R_univ) of theuniverse.)

Therefore, c/R=(13.8 × 10⁹ × (365 × 24 × 3600))-1=22.978×10-19 s-1

However, 1 mega parsec (1Mpc)=3.09 × 10¹⁹ km. Multiplying this value times the value of c/R yields the following:

K0=(22.978 × 10^-19) × 3.09 × 10¹⁹=71.002 km/s/Mpc.

This value (71.002 km/s/Mpc) lies between the currently accepted values of the Hubble constant (calculated by different methods) of 69.8 km/s/Mpc and 74 km/s/Mpc. As the Minkowski-Einstein space-time equation and the Hubble law tell the same story, we should be confident that we are on the right track.

Please note that this derivation of the Hubble constant value is not intended to demonstrate any novel method for finding the Hubble constant value. It is intended to show that the temporal part of space-time metric (both the FLRW and MST metrics) agrees very well with the actual value of the Hubble constant when a (hyper) balloon model of the universe is used. The currently accepted standard model of cosmology overlooks this crucial relationship between Hubble’s law and the space-time metric and thus cannot even explain why the Hubble constant must have the particular value that is actually observed. In fact, it completely ignores what the temporal part of space-time metric (both the FLRW and MST metrics) implies: The entire 3D hypersurface (which is assumed to be synonymous with 3D space) is moving in a direction perpendicular to all of the x-, y-, and z-axes. Time results from this motion along the fourth spatial dimension and time itself is not a dimension (because it does not have units of meters, miles, feet, yards, etc.) The concept of time arises from the formula: Distance (covered)=velocity × time.

This model of the universe (a 3D hypersurface of a 4D sphere, expanding with radial velocity of c in a zero energy balance between motion and gravity) has been used by Suntola.

Results and Discussion

The novel interpretation of the Minkowski space time equation shows that c is the outward expansion rate of our universe, not the velocity of light. This situation is indeed shocking, considering that historically relativity (and the concept of space-time) had its origin in the postulate of the constancy of the velocity of light in vacuum for any observer. Thus, the question arises of how both the velocity of light and the expansion rate of the universe (i.e., the outward velocity of FPHS) can have the same value. In fact, many other physical quantities have the same value c, as Ellis and Uzan point out. That should have been sufficient to raise the suspicion that the velocity c is due to something very deep and fundamental.

Special Relativity (SR) is based on the experimental fact that light travels at a constant velocity (c) independent of the motion of the reference frame. SR does not explain how this postulate comes about. Consequently, even after a century, SR is only in principle a theory and there is no constructive theory explaining it yet.

Moreover, the following questions arise. Is light somehow magical? Is relativity just a branch of electromagnetism? How is it that gravitational waves travel at the same speed of light? (Faced with such embarrassing questions, some scientists have clarified that c is not the velocity of light, but rather the speed of causality. In other words, it is the fastest speed at which two separate parts of the universe can communicate with each other, which clarifies the situation to an extent. However, the question of why has not yet been answered.)

One must ask these questions again. Why is the velocity of light (c) constant? Why cannot anything travel faster than the speed of light?

The real reason is that it is a peculiarity of Minkowskian (hyperbolic) structure.

The Minkowskian spacetime equation ds²=(icdt)²+dx²+dy²+dz²=-c² dt²+ dr² can be re-arranged as follows:

c² dt²=-ds²+dr²=c² dτ²+dr²

This formula is the Pythagorean equation (equation of a right angled triangle; Figure 4).

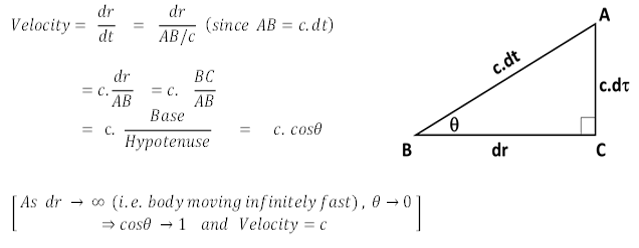
FIG. 4. The Minkowskian (hyperbolic) structure of spacetime limits the velocity of light and gravitational waves to c.

Thus, here is the real reason that nothing can travel faster than the speed of light (which is actually the expansion rate of our universe).

From the above figure, the velocity is given by constant × (base/hypotenuse). Due to the Minkowskian (hyperbolic) nature of space-time, it is imperative that any extremely high velocity be throttled at c. As the base (the distance traveled by the particle) becomes larger, the hypotenuse also becomes larger (time dilation), because, according to the Pythagorean Theorem, the length of the base of the triangle contributes to the length of the hypotenuse.

In other words, because of this particular geometry, if the reference frame is moving fast enough, we start counting spatial distance as temporal distance. We inevitably mix space and time.

In fact, there is no speed limit in the universe (photons can travel at infinite speed). Photons can travel from one galaxy to another without feeling the ticking of time (i.e., the time dilation for the photon becomes infinite and a clock stops for a photon). Alternatively, if we use the formula for length contraction, we can easily see that the distance between one galaxy to the next has shrunk to zero for a photon, so that it can travel instantaneously. If we use the formula for the proper velocity of a photon, we can easily verify that it is travelling infinitely fast. An observer moving at a velocity of 99.999% of the velocity of light (c) also measures the velocity of light as c. This situation is possible only if the velocity of light is infinite (and not with a fixed numerical value of 3 × 10⁸ ms^-1).

If we ignore the dynamical nature of the 3D FPHS-in other words, ignore what the temporal part of the MST equation tells us (which seems natural to trapped beings like us)-then our world indeed appears 3D and Euclidean ds²=dx²+dy²+dz², just as Euclid himself stated.

An immediate consequence of the correction (4D space-time continuum versus dynamic 3D FPHS) is that one dimension becomes free (which we had unnecessarily reserved). Kaluza’s miracle of obtaining Maxwell’s equations in addition to Einstein’s field equations seemed to exact a heavy price: A fifth dimension was needed as an embedding space. However, four dimensions suffice (and we obtain electromagnetic phenomena as a bonus). In fact, the effects of freeing up a dimension are much more profound and resolve the demand for a fifth dimension that appears everywhere in physics, but the strict limitation of the number of dimensions to four, which follows from experiments and observations and simply does not allow a fifth dimension.

The following objections that could be raised against the presented model of the universe all fail miserably.

The presented model is in conflict with the measured flatness of the universe from the CMB using the summation of angles of a triangle (it has already been explained that we need a tetrahedron, not a triangle).

This model is also in conflict with the accelerated expansion of the universe, as claimed in currently accepted ΛCDM model of the universe, rather than a constant rate of expansion, as claimed in this study (more recent studies using a much larger amount of data actually favor a constant rate of expansion of the universe over an accelerated expansion. This finding solves the problem of dark energy. We do not need dark energy because we do not have to account for such acceleration).

The observable universe is itself 94 billion light years across, so the entire universe must be much larger. This argument also fails (this point is explained two paragraphs hence).

Nielsen et al. shows that the available data (from Type Ia supernovae) are still quite consistent with a constant rate of expansion of the universe. Kindly note that this conclusion was drawn from a much larger database of supernovae than those studies that claimed an acceleration of the universe. The evidence for the existence of dark energy has again been challenged by Mohayaee et al., whose analysis used a much larger sample of 740 SNe Ia than that of the original study of 93 Type Ia supernovae from which it was claimed that the universe is accelerating. The existence of dark energy and acceleration of the universe has also been questioned by Nadathur and Sarkar, Colin et al., and Sarkar. Kipreos has shown that after adjusting for the effects of time contraction on a redshift–distance modulus diagram, a linear distribution of supernovae across the full redshift spectrum consistent with a non-accelerating universe is obtained.

This explanation is further supported by Vavrycuk, who show that the FLRW metric describing the expanding universe must be modified to predict the cosmological redshift correctly. The standard FLRW metric creates the illusion of dark energy through supernova dimming.

Overestimation of the size of the observable universe

Bikwa et al. and Li et al. both present arguments that astronomers have greatly overestimated the size of the observable universe. Bikwa et al. claim that the Hubble radius (approximately 13.7 billion light years) is the limit of our observability, even though it is commonly claimed that objects in the Hubble radius have a redshift of only approximately 2, whereas the CMB has a redshift of approximately 1100. Li et al. claim that the earliest observable cosmic radius R (tearliest) is always 0.368 R (where R is the current cosmic radius) and therefore the farthest observable distance is always R–0.368R=0.632R.

The logic (often presented in textbooks) in favor of the observable universe being larger than the Hubble Sphere is the following:

The Hubble constant decreases with time (this is true).

In this way, the Hubble distance increases with time (this is also true).

As the Hubble distance increases, galaxies that were originally outside the Hubble distance and receding from us come inside the Hubble distance (this is where the problem begins).

Imagine a galaxy G1 located exactly on the surface of the Hubble sphere at an early time. Imagine another galaxy G2 lying a little farther behind it.

At a later time, the Hubble distance has increased. However, the distance between us and galaxy G1 has also increased in exactly the same proportion due to stretching of space (therefore galaxy G2 has not yet entered the Hubble sphere). The photon moving towards us would be running on a treadmill due to the expansion of space itself. Using the balloon model of the universe, it is easy to see that the Hubble radius always remains the same as the actual radius of the universe.

Let us assume that the age of our universe is T. Because the radius of our universe is expanding at a constant velocity c, the current radius would be cT.

As we have seen, the Minkowskian structure of spacetime limits the value of the speed of light at c. Therefore, the distance traveled by a photon (Hubble distance)=cT (the fact that our universe was opaque right after the BB due to the strong coupling of radiation and matter is ignored. About 380,000 years later it became transparent, so the farthest distance we can see is slightly reduced. Therefore, the actual size of the observable universe is slightly smaller than the size of the Hubble sphere. However, 380,000 years is quite small and negligible compared to the age of the universe).

A Hubble distance on the hypersurface of the (hyper) balloon universe always forms an angle of 57.2956° at the true center of the universe, which is the BB center.

The claim that the observable universe is much larger than the Hubble sphere is not correct.

The following question was posted on the University of California, Los Angeles website https://www.astro.ucla.edu/~wright/cosmology_faq.html#DN “If the universe is only 14 billion years old, how can we see objects that are now 47 billion light years away?”

The explanation offered for the question begins with the formula for the radius of the observable universe, which it claims is

∫₀^t0 (t/t₀)^-2/3) cdt= 3c t₀ (9)

The simplified explanation stated that another way to look at this situation is to consider a photon emitted by a galaxy that is now 42 billion light years away from us, 14 billion years after the BB. The distance of this photon satisfies the condition D=3ct. If we wait 0.1 billion years, the universe will grow by a factor of (14.1/14)^2/3=1.0048, so the galaxy will be 1.0048 × 42=42.2 billion light years away. However, the light will have traveled 0.1 billion light years farther than the galaxy because it is moving at the speed of light relative to the matter around it and will thus be at D=42.3 billion light years, so D=3ct is still satisfied.

This reasoning is flawed because it assumes that the photon does not have to reach our eye/telescope for the galaxy to be visible. We need to consider a photon (emitted by that galaxy) which is traveling not away from us, but toward us. Consider a photon emitted by the galaxy toward us. After 0.1 billion years, the galaxy will be 42.2 billion light-years away from us. In the meantime, the photon has travelled 0.1 billion light-years toward us and is thus at a distance of 42.1 billion light-years from us.

It started with a distance of 42 billion light-years and after 0.1 billion years it is now 42.1 billion light-years away from us. The more time passes, the farther the distance will increase.

Forget the claim that more galaxies are entering this observable sphere. Can the photon ever reach us at this rate?

(A literature search on cosmology reveals that two mutually contradictory claims are made in the textbooks. 1) Ever more galaxies will enter the observable sphere as time passes. 2) Ever more galaxies will recede away from the boundary of the observable sphere over time.)

Implications of the presented model of the universe

Physics and cosmology are intimately related (e.g., conservation laws of physics arise from the symmetry of nature, as stated by Noether’s theorem). Using this simple shape of our universe, we can directly see why these symmetries (e.g., homogeneity and isotropy) arise in the first place. The model of the universe presented resembles a balloon, or rather, a hyper-balloon. The surface of the balloon looks same everywhere (homogeneous) and from any point on the surface, all directions (along the surface) look basically the same (isotropic).

It is well known to physicists that absolute simultaneity (rather than relative simultaneity) is required by the Sagnac effect, whereas quantum mechanics requires absolute time. From the perspective of the center of the universe, simultaneity is absolute and there is also absolute universal time. That is because the absolute universal time since the Big Bang is just a function of the radius of the universe. From our viewpoint (located at an awkward position in the universe), locality is absolute, and velocity c is the upper limit and remains constant for every observer. Those were Einstein’s firm beliefs, which were later shattered by quantum entanglement experiments (which led to the award of a recent Nobel Prize). This viewpoint turns (our) space and time into inseparable twins and makes (our) time a relative concept. The existence of both absolute time and relative time partially solves the time problem which has so stubbornly resisted the reconciliation of quantum mechanics and GR. In fact, moving the viewpoint to the true center of our expanding universe explains the origin and true nature of time itself.

The radial expansion of the universe appears as passage of time from our perspective. That is because from our viewpoint, the radius of the universe is an impossible direction, which does not even exist for us (thus forcing us to use imaginary numbers) and hence it is a temporal dimension. There is one more point that needs to be discussed regarding this model of the universe. The (entire) closed universe is an absolutely isolated system (True Island) in which total spin, total momentum, etc., must be conserved, however small the magnitude may be. This situation gives rise to non-locality and instant communication over vast distances in quantum-entangled particles. Any open and infinite model of the universe cannot offer a satisfactory explanation of quantum entanglement (which has now secured a firm place in physics and shows no likelihood of being overturned).

Rest-mass momentum

Another consequence of the dynamic 3D FPHS is the concept of rest-mass momentum, which is expressed as

P_rest=m.c. (10)

This concept makes the physics simpler and more consistent (and leads to a unification of the concept of momentum so that we do not have to resort to two sets of rules for calculating the momentum of massive particles and of photons).

This concept was proposed by Haug, but without an explanation why. For a dynamical 3D FPHS (moving at velocity c) and dragging any matter along with it, this concept is built in and integral to the theory. We have never thought about rest-mass momentum because we are moving along with the mass (that we are considering) at the same velocity and in the same direction (hence the relative velocity is zero). However, from the perspective of nature (i.e., from the viewpoint of the center of the universe), the mass m is travelling with velocity c.

Therefore,

Momentum (p)=mass (m). velocity (v)=m.c, (11)

and as explained by Haug, the energy is always

Energy(E)=Momentum (p).c.      (12)

Therefore, rest mass energy is as follows:

E=mc.c=m.c² (13)

That is the true reason for the origin of rest mass energy. We might not have accepted the concept of rest mass energy (E=m.c2) if we had not observed nuclear reactions.

This model is also consistent with other observations, such as the following.

It agrees with the cosmological principle that our (3D) universe is homogeneous and isotropic, which guarantees that Noether’s theorems are satisfied. The surface of a 4D hypersphere is 3D and unbounded (we cannot find an edge to our model universe), just like our own universe.

It seems that there is no center of the universe (although there is indeed a center) and also that the BB seems to have happened everywhere. This model explains naturally why the BB was not an explosion of matter in 3D space, but rather an explosion of space itself.

Objects such as galaxies and galaxy clusters in our universe do not move through space (on average), they move with space. Of particular importance is the form of Hubble’s Law, which shows that everything is moving away from everything else, as if every object is at the center of the universe. This concept fits with this model very well.

The currently accepted SMC does not provide a satisfactory answer to the following question: If our universe is expanding, what is it expanding into? GR assumes that the metric tensor is changing (an analogy is a 3D grid, where the distance between each grid is increasing), but the universe is not expanding into anything. However, this concept is illogical, as the distance between the individual points increases without the overall space (which contains all these points) expanding into anything. The present model gives a satisfactory answer to the above question. Our balloon universe (the term universe is used only for the 3D balloon surface) is expanding into a 4D hyperspace, which could extend infinitely in all four directions. i.e., the hyperspace (void) is possibly infinite, while the matter and fields (the wall of our hyper-balloon universe) have a finite extension and form a closed hypersurface.

Rethinking the BB singularity

The BB model is problematic because if someone let time run backwards and rewound it arbitrarily, then a singularity would inevitably be reached in which the density of matter/radiation would be infinite and the temperature would also be infinite. Everything that exists in the universe today would be confined to a single point, which means a complete breakdown of known laws of physics.

If there had been a singularity in the history of the universe, there would be many observable signatures today. The residual glow of the BB would have temperature fluctuations with enormously large amplitudes. However, the temperature fluctuations are only 1 in 30,000 parts of what the BB singularity would predict. In addition, there would have been copious numbers of magnetic monopoles and other ultra-high energy relics. The constraints imposed by the observations are incredibly tight, so a BB singularity can be ruled out with certainty. This fact strongly suggests that there is indeed a limit to how far the clock can be turned back. One cannot extrapolate to a singularity.

This problem arises primarily because GR is the inside view of a being trapped in 3D space. Consequently, GR has no concept of the outside, or even a concept of an embedding 4D hyperspace. However, as shown in this study, the space-time metrics (both the MST and FLRW metrics) are mathematical statements for embedment of the 3D FPHS, which we call 3D space, in 4D hyperspace. Because GR has no concept of embedding, it also lacks the concept of the thickness of this 3D FPHS. Therefore, GR does not recognize that a balloon wall necessarily becomes thinner as the balloon expands and increases its surface area. If the process is reversed (i.e., the balloon deflates), then the wall becomes thicker and thicker.

Imagine a (rubber) football with a certain wall thickness. As the football deflates, the walls become thicker. However, this process cannot continue indefinitely until the football disappears into a single point. Eventually the wall will become so thick that the inner surface of the wall will converge upon itself (in other words, the empty space inside the football will disappear). The football will then resemble a solid cricket ball.

In 3D, the volume of a sphere is given by (4/3).π.R³ and the area of the surface of the sphere is given by 4.π.R². In 4D, the (hyper) volume of the (hyper) sphere is given by (1/2).π².R⁴ and the volume of the spherical (hyper) surface is given by 2.π².R³. Assuming that the spherical (hyper) surface has uniform thickness Δx everywhere, the (hyper) volume is given by 2.π².R³.Δx.

Further assuming that the hyper volume has remained constant throughout the history of the universe (similar to the case where the amount/volume of rubber in an expanding or deflationary balloon remains constant), the equation to be satisfied is

(1/2).π².(Ri)⁴=2.π².(R_f)³.Δx (14)

The subscripts i and f denote the initial and final (present) radius of the universe. The present radius is approximately 1.30468718385 × 10²⁶ m, which gives

(R_i)⁴=8.88339922756 × 10⁷⁸ × Δx (15)

The value of Δx can be estimated from two different sources. In the course of my research (not yet published), I found that the value of Planck’s length is itself determined by the thickness (Δx) of the 3D FPHS. Hence, Δx should be of the same order of magnitude. Planck’s length is 1.616255 × 10^-35 m (CODATA 2018 value).

Therefore, R_i=1.094261 × 10¹¹ m

The second source for the value of Δx is the estimated value of the (curled up) fifth dimension in Kaluza-Klein theory. (As mentioned earlier, the lack of understanding of imaginary numbers led to the requirement of a fifth dimension. However, to reiterate, what Kaluza and Klein assumed to be the fifth dimension actually turns out to be the fourth dimension). They assumed that the fifth dimension takes the form of a circle and the radius of the circular dimension is 23 times the Planck length, which in turn is of the order of 10⁻³⁵ m.

Therefore, in this case the thickness of the 3D FPHS is given by the diameter of the circular fifth dimension and is thus 2 × 23=46 times the Planck length. It follows that

R_i=1.094261 × 10¹¹ × (46)^0.25 m=1.094261 × 10¹¹ × 2.604290687 m=2.84977 × 10¹¹ m

The average value is given by Ri=1.972 × 10¹¹ m. (Averaging two diverse estimates may not be a good idea, but this estimate isonly meant to be a rough one.)

The above calculation shows that the universe did not originate from a singularity, but rather from a hypersphere with a diameter of 3.944 × 10¹¹ m. That is quite large. At that time, no particles existed in the 3D FPHS and the 4D hypersphere consisted only of fields bursting with energy. Then something mysterious (and still unexplained) happened.

The universe changed from a static 4D hypersphere to a dynamic 3D hypersurface and consequently, the perfect symmetry that existed in nature between the time and space dimensions broke and the flow of time began.

Many physicists have claimed that the second law of thermodynamics (which states that any spontaneously occurring process always leads to an increase in the entropy of the universe) is the most fundamental law. They fail to realize that this law itself results from the expansion of the universe, because entropy and probability are directly related and the expansion of the universe leads to an increase in the volume of our 3D space and thus more possibilities. In fact, the expansion of our universe gives time its arrow and is thus the most fundamental aspect.

When a balloon expands, its surface area increases. However, the volume (quantity) of the rubber remains constant. Similarly, as our universe expands, the volume of 3D space increases, while the hypervolume of the (hyper) balloon remains the same. This concept explains why entropy increases, whereas the crucial unitarity condition of Quantum Mechanics (QM) remains intact (giving us the false impression that time is fully reversible at the fundamental level). This characteristic resolves another deep conflict between QM and thermodynamics (classical physics).

In an upcoming paper, it will be shown that the Schwarzchild metric is also a dynamic 3D FPHS (moving with a velocity c in the fourth dimension), just like the MST metric. The Flamm paraboloid is an accurate mathematical representation of the Schwarzchild metric (contrary to popular belief) if the dynamic nature is considered. Hence, the rubber sheet model (which is used to teach GR in schools and colleges) should be taken literally rather than as an analogy, provided that its dynamic nature is also assumed. The dynamic nature of the 3D FPHS causes the flow of time (which appears to vary with the strength of the gravity field due to varying slopes of the Flamm paraboloid at different distances from the massive object). A hint of the (opposing) effects of this slope on the spatial stretching scale and gravitational time dilation lies hidden in plain sight in the Schwarzchild metric. The scale factors in the temporal and radial part of the metric are negative inverses of each other. This sort of negative inverse relation is seen in the slopes (m1 and m2) of two perpendicular lines (m₁. m₂=–1), which suggests the resolution of the slope into cos(θ) and sin(θ) components. Picturing gravity as a stretching of 3D FPHS rather than a warping of 4D space-time provides a key to unlocking the still mysterious aspects of gravity. The impact of a better understanding of gravity on the subjects of dark matter, cosmic structure, and cosmic evolution shall also be addressed.

Conclusion

Our universe is in the form of a hyper-balloon expanding at a radial velocity of c (the velocity of light). This model overcomes the major challenges faced by the SMC and inherits the successes of the Rh=ct model because it is a constant expansion velocity model of the universe. However, it should be clarified that Melia’s Rh=ct model assumes a flat universe, whereas the presented model is of a positively curved and closed universe.

This study may prompt scientists to measure the thickness of the 3D FPHS precisely. However, the limitation is that the fourth dimension is inaccessible to humans, and hence direct measurement of the thickness may not be possible; thus, some assumption must be made.

This study has opened up the possibility of directly measuring the curvature of our universe (using summation of solid angles of a tetrahedron method) to settle the debate of flat versus curved 3D space forever. In the near future, we could send four space instruments (with extremely sensitive equipment), each of them a million miles apart from the other three, to form a tetrahedron in space. Using laser beams, we could measure the sum of four solid angles and compare it with theoretical values for 3D flat space. In addition to directly measuring the size (radius) of the universe from the curvature value, we could also settle the Hubble constant value debate (because we know the value of c quite precisely).

However, a challenge is that the curvature of the 3D FPHS due to gravitational effects of the sun and also the Milky Way galaxy, is far greater than the overall curvature of the universe itself. The curvatures due to the sun and the Milky Way galaxy are both opposite the direction of curvature of the universe (this discussion requires a separate study and hence will not be elaborated here). However, human ingenuity and complicated mathematics might overcome this challenge. It will be better still if someone figures out a clever method of obtaining the sum of solid angles from the CMB spots. One may measure the solid angle at the apex of the cone whose base is the circular CMB spot.

This study has only hinted at the breathtaking achievements that this model has to offer. Interested readers may wish to consult the preprints.

Funding

This research received no external funding.

Acknowledgments

The figures were drawn for me by my colleague Shri Sanjay Kumar Prajapati (Lattice Design Lab., RRCAT). I would also like to thank Editage (www.editage.com) for English language editing.

Dedication

This paper is dedicated to my mother (late) Mrs. Basanti Waugh, my father (Shri Lalji Vittal Waugh) and to my “Jathamosai” (uncle), who had seen this day coming through his prophetic vision before he left.

Conflicts of Interest

The author declares no conflicts of interest.

References

1. Melia F. A candid assessment of standard cosmology. Publ Astron Soc Pac. 2022;134(1042):121001.

   [Google Scholar]

2. Kroupa P, Pawlowski M, Milgrom M. The failures of the standard model of cosmology require a new paradigm. Int J Mod Phys D. 2012;21(14):1230003.

   [Crossref] [Google Scholar]

3. Kroupa P. The dark matter crisis: Falsification of the current standard model of cosmology. Publ Astron Soc Aust 2012;29(4):395-433.

   [Google Scholar]

4. Efstathiou G. Do we have a standard model of cosmology? Astron Geophys. 2023;64(1).

   [Google Scholar]

5. López-Corredoira M. Tests and problems of the standard model in Cosmology. Found Phys. 2017;47(6):711-718.

   [Google Scholar]

6. Melia F. The cosmic horizon. Mem R Astron Soc. 2007;382(4):1917-1921.

   [Crossref] [Google Scholar]

7. Melia F, Abdelqader M. The cosmological space-time. Int J Mod Phys D. 2009;18(12):1889-1901.

   [Crossref] [Google Scholar]

8. Melia F. The cosmic equation of state. Astrophys Space Sci. 2015;356:393-398.

   [Crossref] [Google Scholar]

9. Melia F, Shevchuk AS. The R h=ct universe. Mon Not R Astron Soc. 2012;419(3):2579-2586.

   [Crossref] [Google Scholar]

10. Wei JJ, Wu XF, Melia F, Maier RS. A comparative analysis of the supernova legacy survey sample with ΛCDM and the Rh=ct universe. Astron J. 2015;149(3):102.

    [Google Scholar]

11. Wei JJ, Wu XF, Melia F. The gamma-ray burst Hubble diagram and its implications for cosmology. Astron J. 2013;772(1):43.

    [Google Scholar]

12. Melia F. The premature formation of high-redshift galaxies. Astron J. 2014;147(5):120.

    [Google Scholar]

13. Melia F. High-z Quasars in the Rh=ct Universe. Astron J. 2013;764(1):72.

    [Google Scholar]

14. Melia F. On recent claims concerning the R h=ct Universe. Mon Not R Astron Soc. 2015;446(2):1191-4.

    [Crossref] [Google Scholar]

15. López-Corredoira M, Marmet L. Alternative ideas in cosmology. Int J Mod Phys D. 2022;31(08):2230014.

    [Crossref] [Google Scholar]

16. Gogberashvili M. Hierarchy problem in the shell-universe model. Int J Mod Phys D. 2002;11(10):1635-1638.

    [Crossref] [Google Scholar]

17. Rubakov VA, Shaposhnikov ME. Extra space-time dimensions: Towards a solution to the cosmological constant problem. Phys Lett B. 1983;125(2-3):139-143.

    [Crossref] [Google Scholar]

18. van de Bruck C. Cosmology and brane worlds: A review. Revue Class Quantum Grav. 2003;20:R201-232.

    [Google Scholar]

19. Xu B, Su J, Wang W. An expanding balloon: A small universe. Phys Ed. 2018;53(6):065005.

    [Google Scholar]

20. Zendri G, Rosi T, Oss S. The Hubble party balloon and the expanding universe. Eur J Phys. 2016;37(5):055701.

    [Google Scholar]