Review
, Volume: 10( 2) DOI: 10.37532/2320-6756.2022.10(2).263Scattering of Perfect Optical Vortex Beams: Physical Unclonable Function
- *Correspondence:
- Bikash Kumar Das
Department of Physics, Technion-Israel Institute of Technology, Haifa, Israel
E-mail: bikash.das@campus.technion.ac.il
Received: December 01, 2021, Manuscript No. M- 48847; Editor assigned: December 4, 2021, PreQC No. P-48847; Reviewed: December 24, 2021, QC No. 48847; Revised: January 15, 2022, Manuscript No. R-48847; Published date: February 5, 2022, DOI: 10.37532/2320–6756.2022.10(2).263
Citation: Bikash Kumar Das, Scattering of Perfect Optical Vortex beams: Physical Unclonable Function, J Phys Astron.2022;10(2):263.
Abstract
Now-a-days, data security has become an important part for anyone connected to the web. Data security ensures that data is getting transmitted securely without any modifications or alterations to the intended receiver. To achieve data security, we have focused on the cryptography which helps to protect our information from being stolen or third-party attacks. Encryption techniques demonstrate an excellent deal of data security when implemented in an optical system such as Holography due to the inherent physical properties of light and the precision it demands. Such systems are somehow vulnerable during their digital implementation under various attacks called crypt-analysis due to the predictable nature of security keys used for the encryption. In this work, we are presenting a Physically Unclonable Functions (PUFs) for producing a robust (stable over time) security key for digital encryption systems. More specifically, we have used the correlation functions of scattered perfect optical vortex beams for the generation of keys which can be used for encryption of data. Here, we convert the 2-D correlation function to 1-D key and digitize based on the average value which will be the random sequence of 1s and 0s. In the best of our knowledge, we are reporting this work for the first time. The experiment and simulation results are well matched.
Keywords
Cryptography; Encryption; Decryption; PUF; Security; Cipher
Introduction
Since last several decades, Cryptography has acquired much popularity for secured transmission of information over an insecure channel like the internet. Information, which needs to be sent, is encrypted in the transmission end and is decrypted in the receiving end using appropriate keys (encrypted and decrypted keys may be same or different depending on the type). An algorithm is usually written for encryption of the information which unites original information with certain number of keys (string of bits) and this algorithm is popularly known as cipher [1]. Initially, classical cryptographic techniques such as symmetric key cryptography (Data Encryption Standard or Data Encryption Algorithm) and asymmetric or public key cryptography (RSA) were employed. In symmetric key cryptography, same key is used for encryption as well as decryption. So, some major difficulties get noticed with this cryptographic technique such as the distribution of key and detection of third parties i.e., eavesdropper which was later solved by quantum cryptography. In public key cryptography, the sender uses public key of the receiver to encrypt the information which is decrypted only with the receiver’s private key. Optical encryption of the information offers a low complexity and higher data rates as compared to electronic encryption. Now-a-days, cryptography is commonly used in various fields such as secured bank transactions, health care, social media, the Internet of Things (IoT), government, security protocols etc. For the first time in 1882, Miller introduced the One Time Pad (OTP) technique which basically uses a perfect random key that is at least as long as the original information. Presently, we are witnessing a constant evolution and change in the field of encryption.
Basically, physical unclonable functions (PUFs) is a physical object that for a given input and conditions (challenges) provides a physically defined “digital fingerprint” output (responses) which serves a unique identifier. PUFs are based on unique physical variations (microstructure) which occur naturally during manufacturing. Advantages of PUFs include (1) easy to evaluate (2) stability over time (3) difficult to replicate (4) impossible to duplicate (cloning of PUFs is impossible). These characteristics of PUFs make us believe that ground glass plate, which is being used for scattering of perfect optical vortex beam, can be used as a PUF device which produces a speckle pattern that can never be cloned.
The correlations in light beams are becoming one of the promising fields of study as it plays a vital role in certain applications such as communication [2,3]. The correlation functions that have singularities are named as “coherent vortices” [4,5]. Recently, these coherent vortices are realized in the intensity correlation of two speckle patterns of different orders [5,6].
As a fundamental attribute that describes statistical properties of random light fields, optical coherence has played an important role in understanding and tailoring light-matter interactions [2, 9]. Information encryption with the help of optical technologies has been studied extensively in the past decade due to remarkable multidimensional capabilities and ultrafast modulation speed afforded by the light fields [10, 11]. Numerous protocols for optical information encryption have been proposed since the double random phase encoding (DRPE) was developed by Refregier and Javidi [12]. Rigorous research on optical information encryption has been carried out till now using the DRPE or DRPE related techniques such as a fractional Fourier domain DRPE [13], lens less DRPE in the Fresnel domain [14], and multidimensional random phase encoding [15]. Recent progress in the light field structure engineering [ 16-18], has highlighted the degrees of freedom of a structured light field as the powerful tools for information encoding. The optical encryption protocols based on the phase structure modulation [19] and OAM and polarization state MDM [20-26] have been developed lately.
In this paper, we proposed a simple and effective method for the generation of Perfect Optical Vortex (POV) speckle pattern by scattering of POV beams through a Ground Glass Plate (GGP) and correlated the generated speckle patterns i.e2-D correlation from which 1-D key has been generated and is used for encryption purpose [7]. For efficient generation of keys, we have used Physically Unclonable Functions (PUFs) and then digitize based on average value which will be random sequence of 1s and 0s. Now-a-days, researchers are using optical technologies for encryption of sensitive information due to multidimensional capabilities of light field. In our work, we use an optical encryption protocol where the information to be sent is encoded with the correlation image of a structured POV beam.
Experiment
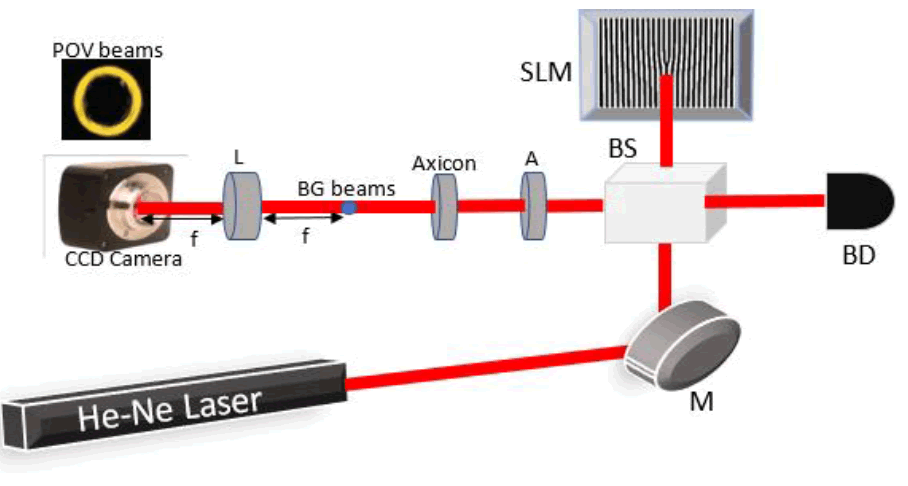
In our experiment, we have proposed the simplest method to generate a perfect optical vortex beam. FIG.1 shows the experimental set up to generate a perfect optical vortex beam and FIG.2 shows the scattering of perfect optical vortex beam through a ground glass plate (GGP) in order to produce perfect optical vortex speckle pattern. A He-Ne laser with a wavelength of 632nm has been used as an optical source which will generate Gaussian beam. The laser beam is made to fall on a reflecting mirror which will be reflected from it and will incident on an unpolarized beam splitter. A spatial light modulator (SLM) in phase only mode has been used which will introduce an optical vortex onto the laser beam. When the spatial light modulator is illuminated by laser beam, an optical vortex beam is produced. The desired beam selected with an aperture (A) is passed through an axicon of apex angle 1780 in order to convert the vortex beam into a non-diffracting Bessel-Gauge (BG) beam. An axicon has been placed at a distance of 50cm from the spatial light modulator. In order to obtain perfect optical vortex beam from Bessel-Gauge beam, a lens of focal length 30cm has been used which will simply perform the Fourier transform (image will be obtained at a very large distance) of BG beam. The intensity distribution of POV beam is recorded through a CCD Camera (FLIR, pixel size 3.45μm) which is placed at the Fourier plane.
Figure 1: (color line) Experimental setup for the generation of perfect optical vortex (POV) beams using a spatial light modulator (in phase only mode) and an axicon. M-Mirror, BD-Beam Dumper, BS-Beam Splitter, SLM-Spatial Light Modulator, A-Aperture, BG-Bessel Gauge, L-Lens, f-Focal Length, CCD-Charge Couple Device.
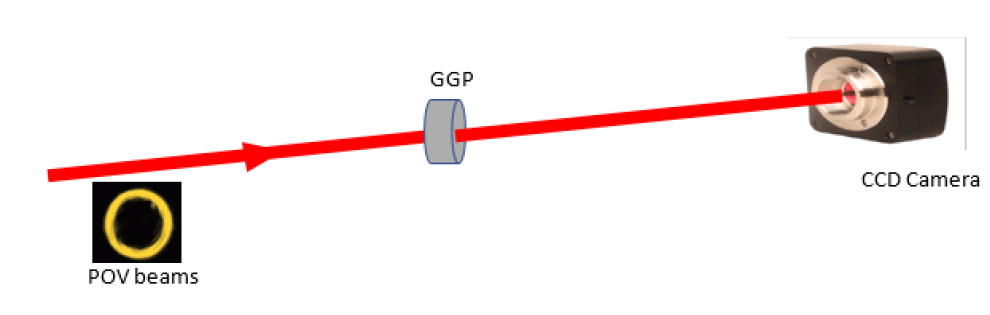
Figure 2: (color line) Experimental set up for generation of speckle from POV beams using ground glass plate and recording the speckle pattern using CCD camera.
The generated POV beams are allowed to pass through a ground glass plate (GGP) (DG10-600, from Thorlabs) for scattering. Ground glass plate is placed at a distance of 72.5 cm from the axicon. Due to interference of many scattered wavefronts, which arise due to the presence of inhomogeneities in GGP, a fine granular pattern of light having randomness is produced and is called as the speckle pattern. Speckle patterns have been recorded at different propagation distances using a CCD camera.
The field which hoists a POV beam having thin annular ring of order m is given by [8],
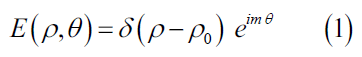
Where ρ0 is the POV beam radius and δ represents the Dirac Delta function having the following properties FIG.3:
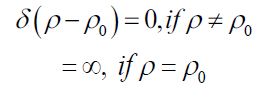
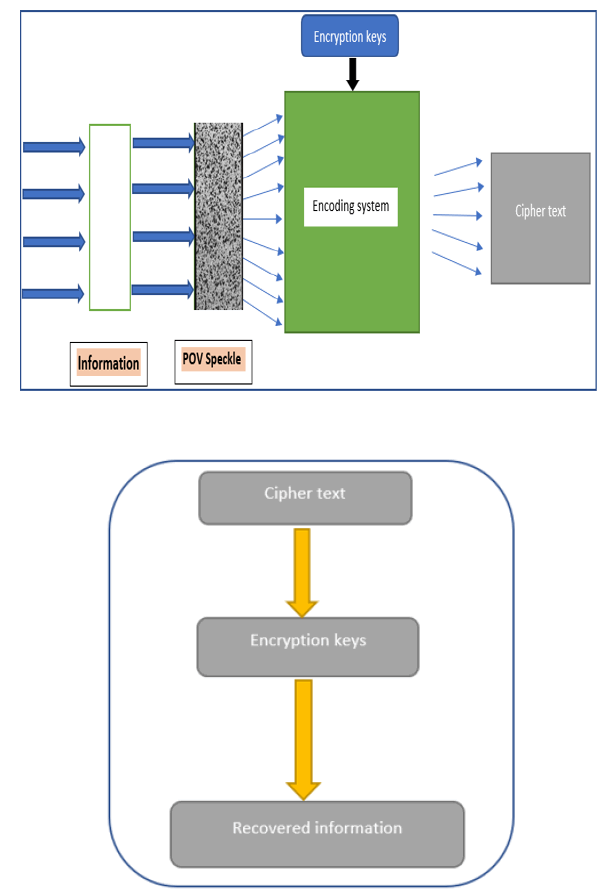
Figure 3: Represents a new optical encryption protocol named as Saroj-Bhusan-Bikash (SBB Protocol) Protocol based on correlation function taken for perfect optical vortex speckles. An information with the correlation function combines with encryption keys forms an encoding system. We generate 2-D correlation image for correlation functions of different order POV beams using MATLAB coding and generate 1-D key from 2-D correlation image using Python. So, after encryption of the piece of information to be sent, cipher text is produced. Same encryption key will be used for decryption of cipher text in order to recover the original information.
A random phase function of eiφ gets introduced in the beam when it is allowed to scatter through a ground glass plate. After scattering of the POV beam through GGP, field distribution of the speckle can be represented as,
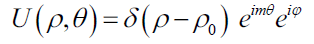
Results and Discussion
In our work, we generate a special class of coherence vortex beam from the scattering of POV beams. The correlation function of the generated coherence vortex is generated by taking the intensity correlation of two speckle pattern corresponding to POV beams of different orders. The generated correlation function is given as,
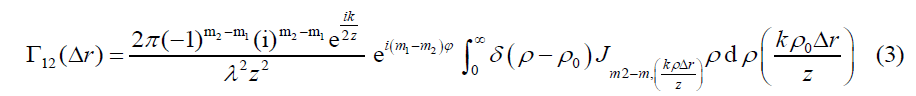
Using equation (2) in the above equation with the help of Anger-Jacobi identity and integral properties of Dirac-Delta function, we get
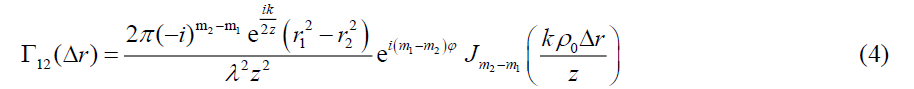
From the above equation, it is clear that the correlation function of two speckle pattern of order m1 and m2 is completely dependent on the Bessel function of order m, where m=m2-m1.
For m1=m2, the cross-correlation function reduces to the auto-correlation function of order 0.
In our work, we have taken different values of m1 and m2 for the generation of correlation image of the speckles and to generate 1-D key from this image. Recent report shows that the Cross Spectral Density (CSD) of a random beam can be viewed as an effective career of an optically encoded information.
We take a ground glass plate as a Physical Unclonable Function (PUF) device which is having random inhomogeneities which are introduced during its manufacturing. PUF devices are difficult to duplicate and unclonable. So, producing two ground glass plates having same randomness is impossible. In our work, we are generating POV speckles by scattering of POV beams through a GGP. So, without the knowledge of the correlation function which depends on Bessel function of specific order and ground glass plate, an eavesdropper can’t access the information which is being sent. In our work, we have used a single encryption key for encoding the information and same key will be used for decoding the information as well FIG.4.
Figure 4: Represents experimentally generated Bessel-Gauss coherence functions of order m=0-2 at a propagation distance of 20 cm from the ground glass plate.
The complexity of measuring the correlation function makes our protocol the best fit for the encryption of the information.
Conclusion
In our work, we have proposed a protocol for optical information encryption into the fourth order correlation of the light fields expressed in terms of the cross spectral density function of the field. We encoded the information with the correlation function of generated POV speckles and found that this protocol enhances the information security as we are taking the help of a ground glass plate as the physical unclonable function device which cannot be cloned further. We found that huge amount of information is needed to reconstruct the cross spectral density distribution. So, the complexity in reconstruction of the cross spectral density distribution enhances the security of the encryption protocol. Our results show that the intensity correlation function of POV speckles of different orders serve as a tool in optical security and optical information security protocol.
References
- Goyal A, Aggarwal S, Jain A. Quantum Cryptography and its Comparison with Classical Cryptography: A Review Paper. In 5th IEEE International Conference on Advanced Computing and Communication Technologies. 2011:1-517.
Google Scholar - Mandel L, Wolf E. Optical coherence and quantum optics. Cambridge university press. 1995.
Google Scholar - Kumar P, Fatima A, Nishchal NK. Image encryption using phase-encoded exclusive-OR operations with incoherent illumination. Journal of Optics. 2019;21(6):065701.
Google Scholar - Wang W, Hanson SG, Miyamoto Y. Experimental investigation of local properties and statistics of optical vortices in random wave fields. Physical review letters. 2005;94(10):103902.
Google Scholar - C R Alves, A J Jesus Silva, EJ Fonseca, Opt Lett. 2015:40;2747.
- Goodman JW. Speckle phenomena in optics: theory and applications. Roberts and Company Publishers. 2007.
Google Scholar - Vanitha P, Lal N, Rani A et al. Correlations in scattered perfect optical vortices. J Optics. 2021.
Google Scholar - Ostrovsky AS, Rickenstorff-Parrao C, Arrizón V. Generation of the “perfect” optical vortex using a liquid-crystal spatial light modulator. Optics letters. 2013;38(4):534-6.
Google Scholar Crossref - AT Friberg, T Setala. Electromagnetic theory of optical coherence (invited), J Opt Soc Am. 2016:33;2431-2442.
Google Scholar Crossref - S Liu, C Guo, J T Sheridan. A review of optical image encryption techniques, Opt Laser Technol. 2014:57, 327-342.
Google Scholar Crossref - Chen W, Javidi B, Chen X. Advances in optical security systems. Adv Opt Photonics. 2014;6(2):120-55.
- Refregier P, Javidi B. Optical image encryption based on input plane and Fourier plane random encoding. Optics letters. 1995;20(7):767-9.
Google Scholar Crossref - G Unnikrishnan, J Joseph, K Singh. Optical encryption by double-random phase encoding in the fractional Fourier domain. Opt Lett. 2000:25;887-889.
Google Scholar Crossref - G Situ, J Zhang. Double random-phase encoding in the Fresnel domain. Opt Lett. 2004:29;1584-1586.
Google Scholar Crossref - O. Matoba, B. Javidi. Encrypted optical memory system using three-dimensional keys in the Fresnel domain. Opt. Lett. 1999:27;762-764.
Google Scholar Crossref - H Rubinsztein-Dunlop, A Forbes, MV Berry, et al. Roadmap on structured light, J. Opt. 2017:19;013001.
- C Rosales-Guzman, B Ndagano, A Forbes, et al. A review of complex vector light fields and their applications. J Opt. 2018:20;123001.
Google Scholar - A Forbes. Structured light from Lasers. Laser Photon Rev. 2019:13;1900140.
Google Scholar Crossref - G Qu, W Yang, Q Song, et al. Reprogrammable meta-hologram for optical encryption. Nat Commun. 2020:11;5484.
Google Scholar - A Trichili, AB Salem, A Dudley, et al. Encoding information using Laguerre Gaussian modes over free space turbulence media. Opt. Lett. 2016:41;3086-3089.
Google Scholar Crossref - X Fang, H Ren, M Gu. Orbital angular momentum holography for high-security encryption. Nat Photon. 2019:14;102-108.
Google Scholar - Z Qiao, Z Wan, G Xie,t al. Multi-vortex laser enabling spatial and temporal encoding. Photoni X. 2020:1;13.
Google Scholar - Y Zhao, J Wang. High-base vector beam encoding/decoding for visible-light communications. Opt Lett. 2015:40;4843-4846.
Google Scholar Crossref - G Milione, TA Nguyen, J Leach, et al. Using the nonseparability of vector beams to encode information for optical communication. Opt Lett. 2015:40;4887-4890.
Google Scholar - M Xian, Y Xu, X Ouyang, et al. Segmented cylindrical vector beams for massively-encoded optical data storage. Sci Bull. 2020:65;2072-2079.
Google Scholar Crossref - H. Larocque, A. D Errico, MF Ferrer-Garcia, et al. Optical framed knots as information carriers. Nat Commun. 2020:11;5119.
Google Scholar