Image Article
, Volume: 13( 1) DOI: 10.37532/2320-6756.2025.13(1).406Newton’s Second Law and Relativistic Hamiltonian Part II. Atomic Terms
- *Correspondence:
- Yuriy Zevatskiy
Department of Astronomy, Saint Petersburg State Institute of Technology, St Petersburg, Russia
E-mail: yuri@newchem.ru
Received: September 14, 2023, Manuscript No. TSPA-23-113826; Editor assigned: September 18, 2023, PreQC No. TSPA-23-113826 (PQ); Reviewed: October 03, 2023, QC No. TSPA-23-113826; Revised: January 09, 2025, Manuscript No. TSPA-23-1 TSPA-23-113826 (R); Published: January 16, 2025, DOI. 10.37532/2320-6756.2025.13(1).406.
Citation: Zevatskiy Y. Newton’s Second Law and Relativistic Hamiltonian Part II. Atomic Terms. J Phys Astron. 2025;13(1).406.
Introduction
The first part of this study reports the calculation of five expressions of relativistic Hamiltonians of particles moving in the field of potential forces depending on the notation of the Newton’s second law. The results obtained were used to calculate terms of ground states of hydrogen-like atoms.
When studying the expression for the range of the proper (local) time Δτ of a moving particle invariant under Lorentz transformations, the first part of this study [1] reports five types of relativistic Hamiltonians. Results are given in Table 1.
| Notation of the Newton’s second law | Expression of the Hamiltonian | |
|---|---|---|
| Fdr ≠ 0 (I) | Fdr = 0 (II) | |
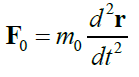 |
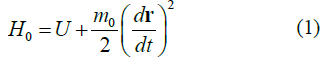 |
|
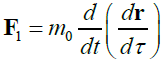 |
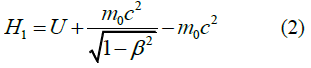 |
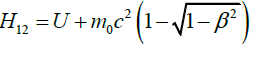 |
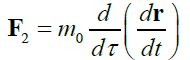 |
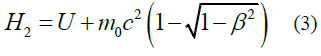 |
|
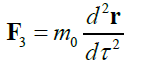 |
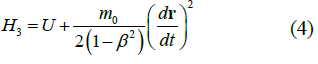 |
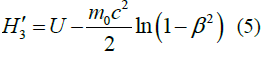 |
TABLE 1. The expression of the Hamiltonian of the particle motion depending on the notation of the Newton’s second law and characteristics of its path.
Discussion
Second summands in equations (1-5) are expressions of the kinetic energy of a particle in the field of potential forces at the value of its potential energys U.
On expanding in a power series β, these summands give the series in which only the first members of the equation coincide (m0v2/2). The difference in values of the kinetic energy, calculated for example by equations (1) and (5), at β=0.1 equals 0.3 %, while at β=0.5 it reaches 7.5 %.
The applicability of the considered formulas to calculate the Hamiltonian can be assessed in the context of calculating the terms of hydrogen-like atoms. Clearly, due to the fact that electrons in the atom have no trajectory, it is impossible to accurately determine Fdr ≠ 0 or Fdr=0 in their state. It can be only assumed that for electrons with a high orbital quantum number (l), the second condition Fdr=0 (II) is more satisfied than the first one Fdr ≠ 0 (I). It can also be affirmed that the terms of hydrogen-like atom will be within the range of Hamiltonian values, corresponding to conditions (I) and (II) regardless of the quantum numbers of the electron. To verify this provision, one can use the results of the study [2], where it was proved that regardless of the kind of the electron kinetic energy, the atomic term takes on a minimum when the distance from any electron to the nucleus ri is related to its principal quantum number ni and nucleus charge Z, by the equation

Unless otherwise noted, hereinafter atomic units will be used. Values of fundamental constants h=1, e = 1, me=1, c=α-1 is a fine structure constant), energy is expressed in Rydberg.
Shall the quantum conditions of the state of an electron in an atom be satisfied, one has the equation

It follows that
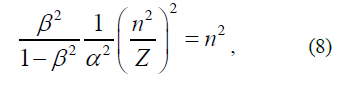
Wherefrom we find
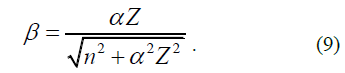
The term of a hydrogen-like electron T is calculated as a sum of kinetic energies of an electron (Ee) under its motion relative to the nucleus, the potential energy of their charges (U) and the kinetic energy of the relative motion of the atom (E). Preliminary calculations showed that the kinetic energy E can be taken into account classically:
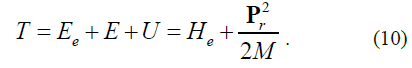
M - atomic mass in terms of the electronic mass.
Below are the formulas to calculate terms using all fives expressions of the Hamiltonian (1-5) of the electron He in hydrogen atoms (M=938.272 MeV), deuterium (M=1875.613 MeV) and tritium (M=2808.921 MeV [3]).
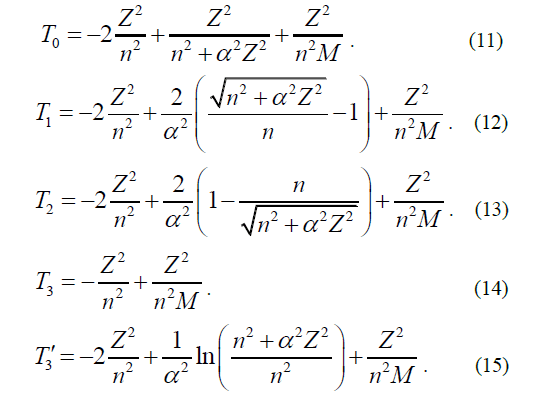
When calculating the limiting values of the terms of H, D and T, it should be assumed that Z=1 and n=1, since this corresponds to the deepest state of 1S electron.
The calculation results in comparison with the experimental data [4] are shown in Table 2.
The listed data shows the discrepancy between the estimated and experimental values of terms, thus it can be seen that the term with the use of the Hamiltonian H1 gives the best agreements with the experiment. The estimated faulty proportion in order of appearance corresponds to the amount of the Lamb shift in the atom, however it exceeds its value.
| Atom | Hydrogen (H) | Deuterium (D) | Tritium (T) | |||
|---|---|---|---|---|---|---|
| Term | Value | Texp–T,10-6 | Value | Texp–T,10-6 | Value | Texp–T,10-6 |
| – Texp | 0.9994665084 | - | 0.9997384561 | - | 0.99982894 | - |
| – T0 | 0.9995089279 | 42.4195 | 0.9997808790 | 42.4230 | 0.99987136 | 42.4216 |
| – T1 | 0.9994689919 | 2.4835 | 0.9997409430 | 2.4869 | 0.99983143 | 2.4856 |
| – T2 | 0.9994956161 | 29.1077 | 0.9997675673 | 29.1112 | 0.99985805 | 29.1098 |
| – T3 | 0.9994556794 | -10.8290 | 0.9997276305 | -10.8256 | 0.99981811 | -10.8269 |
| – T3' | 0.9994823041 | 15.7957 | 0.9997542552 | 15.7992 | 0.99984474 | 15.7978 |
TABLE 2. Estimated and experimental values of low-lying terms of hydrogen-like atoms (are expressed in Rydberg).
Based on the above-mentioned considerations on the uncertainty of the electron motion in an atom, we can assume that the observed state of an electron is a superposition of states corresponding to the adherence to specifications (I) and terms (II). Thus, the observed Hamiltonian of the electron in the atom.
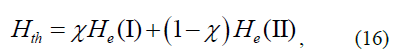
where χ is the contribution of the state (I), while (1-χ) is the contribution of state (II) to the electron motion? It is obvious that it is impossible to use this state under the classical (1) and inverse relativistic (3) expressions of the Newton’s second law, as in these cases Hamiltonians I and II are degenerated.
H0(I)=H0(II), H2(I)=H2(II)=H12 (Table 1).
A pair of states (I) and (II) cannot serve this purpose when using the Newton’s second law (2) in the forms, suggested by Lorentz because of the difference between H1(I) and H1(II) with experimental values of the same op-erator (Table 2).
Only a pair of Hamiltonians H3 and H3' can provide the full correspond-ence of Hth, calculated by the formula (16) to experimental values. Assuming
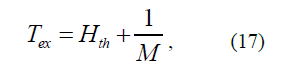
one can get values χ for 1S electrons in considered atoms.
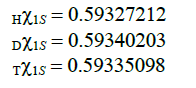
By similar considerations, one can seek the Lamb shift in atoms. Under that logic, one can assume that for P-electrons the contribution of the state (II) to the motion is higher than that for S-electrons. Consequently, the in equation χs>χp will be fulfilled at one value for the principal quantum number n. The conclusion matches up with the observed facts. Shall all other conditions (quantum numbers) be equal, the kinetic energy of S-electrons will be slightly higher than that of P-electrons. In particular, it will result in splitting of the terms of hydrogen-like atoms with electron 2S and 2P at the same value of j–total angular momentum of the electron in the atom. Formulas to calculate the atomic terms in the indicated states are (14) and (15), where Z=1, n=2:
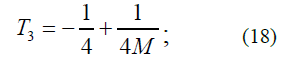
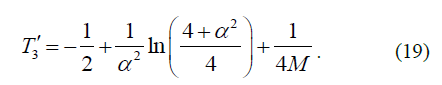
The observed value of the term of the state of an atom with the principal quantum number n=2 is found according to equations (16) and (17) using the formula:
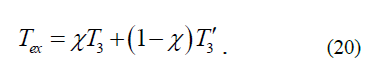
However, a comparison of the precision experimental values of the terms of hydrogen and deuterium atoms [5] in the state with n=2, l=1, j=½ and in the state with n=2, l=0, j=½ revealed the following (l is an orbital quantum number). All these values turned out to be outside the range of the energy values [T3, T3'], determined by formulas (18) and (19). Nevertheless, the experimental values of terms of hydrogen and deuterium atoms in the state with n=2, l=1, j=3/2 turned out to be almost surely in the middle of the range [T3, T3'].
The comparison of estimated results and experimental data [5] are shown in Table 3. Values Hχ2P and Dχ2P, determined by the formula (20) for hydrogen and deuterium atoms in the state with n=2, l=1, j=3/2, almost coincided up to the sixth significant figure:
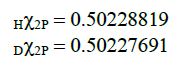
In the same place, Table 3 shows the values of the terms, calculated using the equation (12) (Lorentz formula), in which it is assumed: Z=1 and n=2. The value of the Rydberg constant R∞·c=3,2898419602508·1015 Hz.
Noteworthy is the rather low error in calculating the atomic terms in the state with n=2, l=1, j=3/2 using the Lorentz formula (12). However, the indicated error for the hydrogen atom (12531 kHz) exceeds the error of the experimental determination (5,5 kHz) [5] by several orders of magnitude. The indicated error of the deuterium atom (12469 kHz) also exceeds the error of the experimental determination (5,5 kHz).
Therefore, the final answer to the question concerning the applicability of the Hamiltonians in the form (2) or (4) and (5) to solve the problem of atomic terms is possible only after solving the problem of calculating the Lamb shift for states with j=½.
| Atom | Hydrogen (H) | Deuterium (D) | ||
|---|---|---|---|---|
| Term | Value | Texp–T | Value | Texp–T |
| – Texp, kHz | 82201553274.3 | - | 822239201737.3 | - |
| – Texp, Ryd | 0.2498647481 | - | 0.2499327359 | - |
| – T1, Ryd | 0.2498647519 | -3.8089·10-9 | 0.9997409430 | -3.7902·10-9 |
| – T3, Ryd | 0.2498639199 | 8.2824·10-7 | 0.9997276305 | 8.2826·10-7 |
| – T3', Ryd | 0.249865584 | -8.3585·10-7 | 0.9997542552 | -8.3583·10-7 |
TABLE 3. Estimated and experimental values of terms of hydrogen-like atoms in states with n=2, l=1, j=3/2.
References
- Yuriy Zevatskiy. Newton's Second Law and Relativistic Hamiltonian II: Atomic Terms (May 18, 2021).
- Zevatskii YE. Technical Physics, 2006, Vol. 51, No. 3, pp. 378-382.
- Nuclear Wallet Cards database version of 7/10/2019
- NIST. Atomic Spectra Database. NIST Standard Reference Database 78. Version 5.8.
- NIST. Energy Levels of Hydrogen and Deuterium. NIST Standard Reference Database 142. Last Update to Data Content: July 2005.

