Current opinion

, Volume: 10( 1) DOI: 10.37532/2320-6756.2022.10(1).259

• View PDF
• Download PDF

Different Approaches to the Fundamentals of General Relativity

*Correspondence:

Ali Riza Sahin
Istanbul Ataturk Anatolian High School, Istanbul, Turkey,
E-mail: arizasahin@gmail.com

Abstract

While efforts to find solutions to the famous problems of general relativity theory continue, we ask three new fundamental questions that can be considered in addition to these problems without getting lost in the depths of general relativity theory. These questions involve the principle of equivalence (the most basic principle of the theory), the boundary condition between general relativity and Newtonian gravity, and the Schwarzschild metric, which is accepted as the simplest solution in general relativity theory. When we try to address these questions, we see that the answers contradict the foundations of general relativity.

Keywords

General relativity; Gravitation; Metric; Metric tensor; Einstein equations; Schwarzschild metric; Equivalence principle; Stress-energy tensor

Introduction

Einstein's general theory of relativity is generally accepted as correct in the scientific world, and despite the problems associated with it, scientists have preferred not to move away from the general structure of the theory. Although efforts to address these problems and to find solutions have an important place in the scientific world, the general tendency is to remain within the basic structure of the general theory of relativity. However, as this understanding continues, it is clear that the problems that have persisted in the scientific world for nearly a century will continue. The complexity of the mathematical foundations on which the general theory of relativity is based, the difficulty of testing the results of scientific studies based on this theory, and the reluctance of other scientists to criticize the theory developed by the world's most famous physicist may be among the reasons for this situation. In the literature, there are many studies dealing with general relativity problems. These include [1-3], and a huge list of others. This is significant, as it shows that there is an obvious problem with the general theory of relativity. However, although most of these studies are in the same vein as this study in that they address the problems with general relativity, they do not have a great deal of similarity with this study in terms of the problems we deal with and the results. In this paper, we will try to express some of the contradictions in the basic assumptions and results of the general theory of relativity, since many physicists have tried to raise questions about the general theory of relativity in other ways. Unlike these scientists, we will not plumb the depths of the theory, but will start from the very beginning. In order to make our work easier to understand, we will try to do this as far as possible without getting stuck in mathematical calculations or equations, and without getting lost in the complexity and depths of general relativity theory. We believe that enough work has been done to address the profound and complex problems of the general theory of relativity. In short, our priority is to be understandable. First of all, we consider Einstein's equivalence principle. Next, we will consider the boundary condition in which general relativity converges to Newtonian gravity. Finally, we will look at the Schwarzschild metric, which is the most well-known solution to general relativity theory and which plays the most important role in the acceptance of this theory, from a different perspective.

Three Confusing New Questions and Problems for General Relativity

Is the principle of equivalence valid only for gravitation?

It is well-known that the principle of equivalence is the most important starting point for the general theory of relativity. Rather than considering the validity of this principle and the extent to which it is true, it would be wiser to ask the questions that Einstein did not ask: Does the equivalence principle only apply to gravity? Or would any interaction produce the same effect? In Einstein's famous thought experiment of the free-falling elevator, if we cannot distinguish whether the elevator is in free fall due to gravity or is in motion under acceleration, we also cannot distinguish whether this elevator is an electrically charged object and whether it is attracted by electricity. Likewise, we cannot distinguish whether it is under the influence of other forces, either known or unknown. We can clarify this with an alternative thought experiment. Let the earth be positively charged and all objects on it be negatively charged. Assuming that the electric field outside the earth is constant, in the same way as we assume that the gravitational acceleration g is constant, a person in a free-falling elevator will perceive both scenarios as being the same, regardless of whether the drop is due to gravity or the electric field. Now that we have solved this problem in our minds, let us get back to the answer to our question. The answer is no the equivalence principle must be valid not only for gravity, but also for other interactions. However, this expectation will bring many new results. For example, if gravity bends space-time, other interactions must also bend space-time. The Einstein tensor should not only include gravity, but should be more general. Hence, Einstein’s equations should not only explain gravity, but should also explain all interactions in general, or at least in the realm of electrodynamics. In fact, the idea we have expressed above is not far from the truth, as the operations performed to calculate the curvature of space-time are purely mathematical and there are no restrictions on interactions. Since the curvature of space-time is calculated independently of any interaction, this curvature is related to the interactions that take place in that space-time and the properties of matter there. If only mass exists, we can be sure that the curvature of space-time is related to gravity, but if there is a charge and/or electric current in space-time (assuming no mass for now), then we can say that the space-time curvature we calculated is directly related to electrodynamics. In the second case mentioned above, i.e., if there is an electric charge and current in space-time, it is inevitable that there will be a result that we know very well. Although we do not know what kind of metric tensor or metric to use for space-time in case of electric charge and current, the Einstein equations we will find as a result of complex operations should give us the stress-energy tensor for electrodynamics. This means that there must be a metric or metric tensor by which we can express the electrodynamics [4].

Is there a different way for the boundary condition between general relativity and Newtonian gravity?

We know that the equations by which Einstein relates the curvature of space-time to gravity take the form,

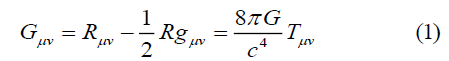
where G_μν is the Einstein tensor, gμν is the metric tensor, R_μν is the Ricci curvature tensor, R is the scalar curvature (or the Ricci scalar),G is the Newtonian constant of gravitation, c is the speed of light in vacuum and T_μν is the stress-energy tensor.

The middle term of (1), which is calculated by complex mathematical operations, is completely independent of any interaction, and covers the most general case (we ignore the cosmological constant here, as it does not affect our purpose). However, the rightmost term 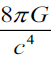, also known as the Einstein gravitational constant, is entirely based on Einstein's assumption that the bending of spacetime is a result of gravity, and is therefore somewhat arbitrary. We mentioned in the previous section that we can also apply this arbitrariness to other interactions, but what we really want to do here is examine the boundary condition that takes us to the rightmost term of (equation 1). After Einstein assumed that Gμν was related to gravity, he used Newton gravity as a boundary condition to connect it to gravity mathematically and physically. Einstein thought that Newton's gravity was correct for a weak gravitational field, and that general relativity should approximate Newton's results for a weak gravitational field. These approaches can be summarized mathematically as:

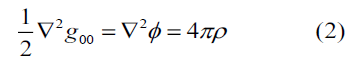
∇ is the Laplacian, φ is the Newtonian gravitational field and ρ is the density of matter. As can be seen from (equation 2), in general relativity, metric tensor elements play the role of fields. This is a result of Einstein's weak gravitational field approach, in which the weak field allows us to write the metric tensor as the sum of a flat space-time and a space-time metric to give the gravity, as follows:

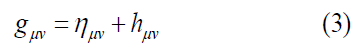
Where,

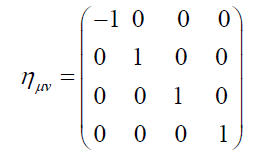
and h_μν is a perturbation term due to weak gravity. If we examine (equation 3) carefully, ignoring the approaches offered as solutions in general relativity, it is quite unusual to construct a metric tensor that is the sum of two terms, as the metric tensor is usually obtained by multiplying several terms. For example, for the line element of a space, this takes the form

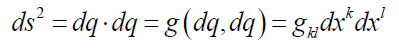
Hence, instead of writing the metric tensor as the sum of the two tensors, we prefer to write it as the product of the two terms, as follows:

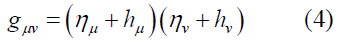
where η = (1,1,1,1) and h is a perturbation term due to weak gravity. The term η denotes flat space-time, whereas the term h_μ denotes the perturbative effect of the mass on g_μν , which creates a weak gravitational field in this space-time. Since our focus here is on g₀₀ , the other elements of h_μ are not very important. Note that (4) gives the Newtonian boundary condition as follows:

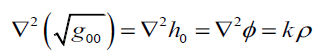
Where k is a constant coefficient. Thus, we have presented an alternative to Einstein's idea that g_μν serves as a field for gravity. Our approach also has a more important consequence: it demonstrates a new way of positioning fields in the metric tensor, or general relativity. In particular, the fact that 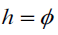indicates that expressing the metric tensor as the product of several fields may be a more appropriate link between general relativity and field theory [4].

Does the Schwarzschild metric contradict itself?

There is no doubt that the Schwarzschild metric, the best known and simplest solution to Einstein's equations, has a special place in the general theory of relativity. This metric, which strengthened support for general relativity and Einstein's reputation in the scientific world, has been used to predict events such as redshift, perihelion, time delay and light aberration with results that are very close to observations. Naturally, it is quite difficult to call this criterion, which has existed for more than a century and cannot be changed, problematic. However, we will ask whether there is a problem with the Schwarzschild metric, and will answer this question after recalling several points.

The well-known Schwarzschild metric is given by

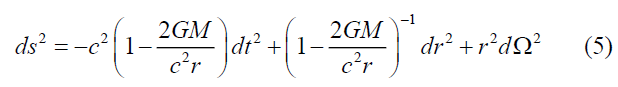
Since (5) was derived for weak gravitational field, it is also based on Einstein’s Newtonian boundary condition; that is, there is a static, constant mass that generates a weak gravitational field. Briefly, we are sure that there is a Newtonian gravitation field in space. We can rewrite (5) in terms of as

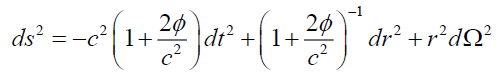
Even within the confines of classical mechanics, if a Newtonian gravitational field 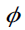exists, it must satisfy 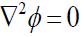in space outside the mass. The stress-energy tensor that gives this equation of motion is then as follows:

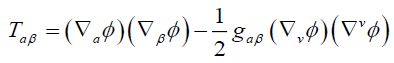
Although we have written as 4 × 4 tensor, we will only deal with T₀₀ for weak gravity (g_μ = diag (−1,1,1,1) due to weak gravitation). This is expressed as:

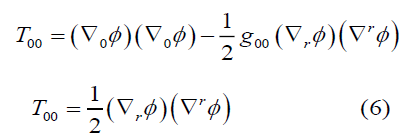
As can be seen, T₀₀ is not zero in the weak field approximation. In fact, this is the equivalent of the approach proposed in the previous section. Although the approach set out in the previous section is purely a mathematical choice, we see here that there is a physical necessity that the stress-energy tensor does not disappear if there is mass in space (if T₀₀ = 0 , this means that 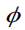= constant). Logically, we believe that this should be the correct Einstein boundary condition between general relativity and Newtonian gravity. Returning to the Schwarzschild metric, we are faced with a very serious contradiction. The Schwarzschild metric is a solution to Einstein’s equations in a vacuum, and it is therefore accepted that G_μν=kT_μν = 0 However, as mentioned earlier, even if there is a weak gravitational field in space, 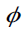displays itself in metric and other places. In brief, G_μν = kT_μν ≠ 0 . Hence, the Schwarzschild metric contradicts itself, and is therefore rather problematic.

Conclusions

In the previous section, we touched upon the points that we see as missing or wrong in the general theory of relativity by means of three separate questions. The first point is that we should consider the equivalence principle for all interactions; if we do this, the idea that we can express electrodynamics through the curvature of space becomes inevitable. The second is that we could express the boundary condition between general relativity and Newtonian gravity in a different way. If we do not do this, we come to the conclusion that new paths are opened regarding the place of fields in the metric tensor and in general relativity, and that we can reduce general relativity to some fields from the metric tensor. Our final result was that the Schwarzschild metric contradicts itself.

Regardless of whether the interaction is strong or weak, if there is a mass that creates a gravitational field, G₀₀ = T₀₀ = , where T₀₀ is an element of (equation 6).

Obviously, we could add more general relativity problems at a higher and more complex level, but this would not contribute to finding solutions to the existing problems. Over the last century, there have been many studies that have supported basic relativity or have reported new results based on it, as well as studies that have focused on the problems of general relativity. Unfortunately, the group of scientists working in support of general relativity hope to solve the problems of this theory by complicating the theory even further. The main problem is with the general theory of relativity itself, and it is introduced at the very beginning of the theory. Despite the revolutionary changes it has wrought in our understanding of science and its success in explaining events that classical mechanics could not explain, it falls short of opening up new horizons for science. In addition to the shortcomings of the general theory of relativity, it almost completely separates gravity from other interactions, and plays a negative role in unifying the four fundamental interactions. Moreover, its incompatibility with field theory does not allow for an analysis of general relativity within the framework of quantum mechanics. Every idea or theory that has been used or has offered benefits throughout human history is like a train that carries humanity from one station to another. The general theory of relativity has revolutionized our understanding of physics and nature and has moved us many stations forward. Clearly, it is time to take a new train and travel to new stations. The thoughts that we express may be very speculative, inaccurate, or not important at all. However, the obvious truth that many scientists have been trying to articulate for years is clear: the general theory of relativity is inadequate and obstructs us from attaining new scientific information.

References

1. Hatch RR. A new theory of gravity: Overcoming problems with general relativity. Physics Essays. 2007;20(1):83-100.
   

   [Google Scholar]          [Crossref]

2. Havas P. Foundation problems in general relativity. In delaware seminar in the foundations of physics. Springer, Berlin, Heidelberg. 1967:124-148.
   

   [Google Scholar]         [Crossref]

3. Smarandache F, Yuhua F, Fengjuan Z. Unsolved problems in special and general relativity. Infinite Study. 2013.
   

   [Google Scholar]         [Crossref]

4. Ali R?za Sahin, New Horizons in Mathematical Physics. 2021;5(2):1-10.
   

   [Google Scholar]             [Crossref]