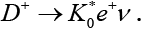Original Article
, Volume: 5( 1)D Meson Decays and New Physics
- *Correspondence:
- Kabuswa Davy M, Institute of Particle Physics, Central China Normal University, China, Tel: +862767863760; E-mail: davymanyika@yahoo.com
Received: April 17, 2017; Accepted: April 27, 2017; Published: May 2, 2017
Citation: Kabuswa Davy M, Xiao BW. D Meson Decays and New Physics. J Phys Astron. 2017;5(2):110.
Abstract
On one hand, we investigated the decay rates of meson decays from the basic computations of the Feynman diagrams. Under this approach, we derived analytically expressions for the square amplitudes of leptonic and semileptonic decays and finally used them to determine the analytical and numerical results for the decay rates. With decay rates results at our disposal, we determined the branching ratios of leptonic and semileptonic decays separately within the standard model (SM) compared our results to the latest theoretical and experimental results. On the other hand, we focused on the effective Lagrangian (EL) under weak interaction from a general approach and used it in our calculation of differential decay rates of mesons. Thereafter, we calculated the total decay rates via integration with respect to. In addition, using the total decay rates results, the branching ratios and the contributions from the new physics (NP) operators were investigated resulting in some phenomenologies of physics beyond the SM.
Keywords
Dmeson; Leptonic decay; Semileptonic decay; New physics
Introduction
From theory and experiments, there are several arguments to believe that the SM is just the low energy limit of a more fundamental theory. This is not necessarily true because the SM has been successfully tested at an impressive level of accuracy and provides at present our best fundamental understanding of the phenomenology of particle physics. During the 20th century, physicists made tremendous progress in observing smaller and smaller objects and today’s accelerators allow us to study matter on length scales as short as 10 m to 18 m [1].
The basic questions of particle physics are:
1. What is the world made of?
2. What is the smallest indivisible building block of matter?
3. Is there such a thing?
A major goal of physics is to find a common ground that would give an integrated approach and understanding on how to solve these questions surrounding nature [2].
Despite the high level of consistence and accuracy within the SM, it does leave some phenomena unexplained and it falls short of being a complete theory of fundamental interactions [3]. Therefore, the answer to these challenges lie in probing more of physics beyond the SM [4].
D Meson Decays
D mesons contain quarks and are one of the lightest particles in this family [5].
Leptonic Decays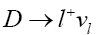
The purely leptonic charged D meson decays are the easiest to analyze among its decays. The factorization of its hadronic dynamics is given by
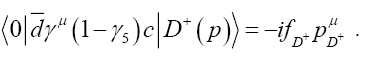 (1)
(1)
Figure 1 shows the process of a D+ meson decaying into a lepton and a neutron pair. Starting with the computation of the amplitude from the Feynman diagram, we arrive at the structure of the decay width to lowest order as
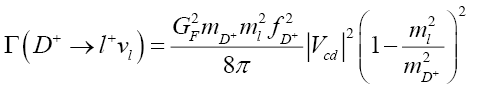 (2)
(2)
From equation (2) the Fermi constant is given by GF , the D+ From equation (2) the Fermi constant is given by GF , the D+ meson mass by 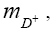 and the lepton mass by
and the lepton mass by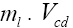 is the CKM matrix element and
is the CKM matrix element and 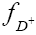 is the decay constant.
is the decay constant.
Analyzing equation (1), it is evident that there are no leftover variables in our decay rate calculation under the leptonic decay in question. Thus, the branching ratio is determined straight forwardly without any integration by multiplying the decay rate to the mean life, 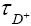
Semileptonic Decays
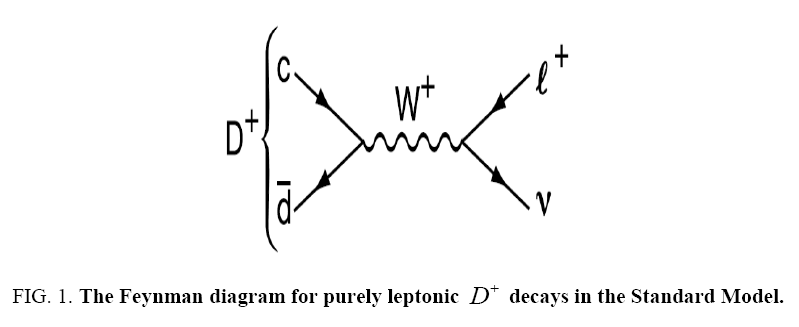
Due to the fact that leptons do not involve strong interaction, the lepton pair is free from the strong binding effects in the semileptonic decays. Consequently, we can factor them out and arrive at
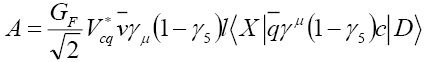 (3)
(3)
In the above expression, 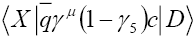 include all strong interactions. Leptonic and semileptonic D meson decays are ideal laboratories to study non-perturbative QCD, and to determine important quark mixing parameters. In addition, they may provide additional constraints on physics beyond the SM.
include all strong interactions. Leptonic and semileptonic D meson decays are ideal laboratories to study non-perturbative QCD, and to determine important quark mixing parameters. In addition, they may provide additional constraints on physics beyond the SM.
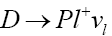 Decay: Within the Standard Model, the D meson semileptonic decay amplitude is given by [6]
Decay: Within the Standard Model, the D meson semileptonic decay amplitude is given by [6]
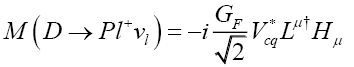 (4)
(4)
with 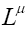 being the leptonic current and
being the leptonic current and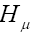 the hadronic current describing weak and strong dynamics of the interaction, respectively. Here the leptonic current is defined as
the hadronic current describing weak and strong dynamics of the interaction, respectively. Here the leptonic current is defined as
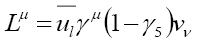 (5)
(5)
Where u1 and vv are the lepton and neutrino Dirac spinors, respectively. On the other hand, the hadronic current can be written as
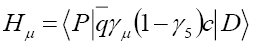 (6)
(6)
It is vivid that D semileptonic decays involve the non-perturbative effects of quantum chromodynamics (QCD). As a result, this matrix element cannot be solved analytically. However, it can be parameterized by expanding the current in terms of all possible independent 4-vectors that can describe the decay, with each of these multiplied by a Lorentz-invariant form factor.
In our case, there are only two independent 4 -vectors, which can be taken to be 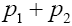 and
and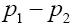 . Moreover, there is only one Lorentz invariant quantity, which is traditionally taken to be the invariant mass squared of the virtual W boson,
. Moreover, there is only one Lorentz invariant quantity, which is traditionally taken to be the invariant mass squared of the virtual W boson,
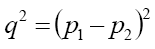
Thus,  can take a decomposed in the form
can take a decomposed in the form
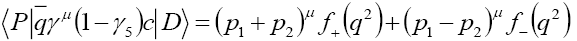 (17)
(17)
with p1 and p2 being the initial D momenta and and pseudoscalar meson in the final state, respectively. From above, the form factors are given by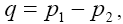 and
and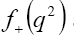 and
and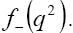 We can also express the decomposition in the form
We can also express the decomposition in the form
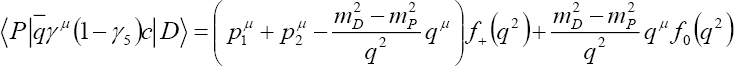 (8)
(8)
with 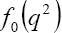 being the scalar and
being the scalar and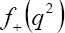 the vector form factors, respectively.
the vector form factors, respectively.
Here we note that 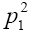 and
and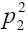 are not variables since the initial and final particles are on-the-mass-shell;
are not variables since the initial and final particles are on-the-mass-shell;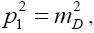
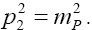 The form factors depend only on
The form factors depend only on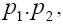 and hence for we can write an equivalently relation as
and hence for we can write an equivalently relation as
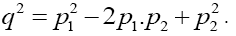 (9)
(9)
With an electron in the final state, its mass is much less with respect to parent D, therefore, only 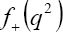 contributes. As a result, taking the limit
contributes. As a result, taking the limit 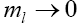 is an excellent approximation, and the current is further simplified to
is an excellent approximation, and the current is further simplified to
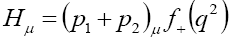 (10)
(10)
Using these expressions for the hadronic and leptonic currents, we arrive at the partial decay width:
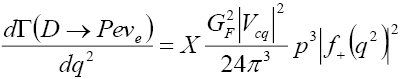 (11)
(11)
with p and X being the hadronic momentum and multiplicative factor, respectively. By neglecting lepton masses and plugging in all the necessary parameters we arrive at
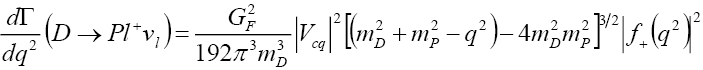 (12)
(12)
with only 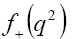 contributing.
contributing.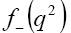 contributions are neglected due to its proportionality relation with
contributions are neglected due to its proportionality relation with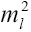 . Here
. Here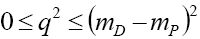 gives the q2 distribution range.
gives the q2 distribution range.
Experimental studies measure 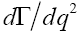 integrated over several q2 bins in each semileptonic mode. In order to compare these with theoretical predictions, which provide estimates of
integrated over several q2 bins in each semileptonic mode. In order to compare these with theoretical predictions, which provide estimates of 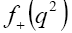 at one or several points in q2 , it is convenient to fit the results using parameterizations of
at one or several points in q2 , it is convenient to fit the results using parameterizations of 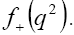 Theoretically, a number of parameterizations of
Theoretically, a number of parameterizations of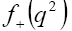 have been suggested. The most theoretically motivated one is known as the "series" parameterization [7] and follows from a dispersion relation:
have been suggested. The most theoretically motivated one is known as the "series" parameterization [7] and follows from a dispersion relation:
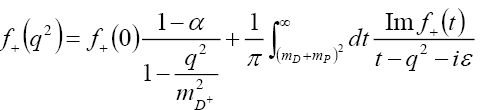 (13)
(13)
with 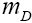 and
and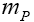 being the parent and daughter masses, respectively, and α is related to the relative meson contribution to
being the parent and daughter masses, respectively, and α is related to the relative meson contribution to 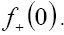
Here we are not going to dwell much on this one but on another parameterization called ‘simple pole’ model which suggests that the dispersion relation given in Eq. (13) is described by
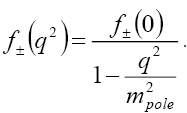 (14)
(14)
While this model can provide reasonable fits when both 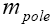 and
and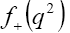 are allowed to float, experimental fits of
are allowed to float, experimental fits of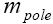 are far away from the expected value of
are far away from the expected value of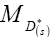 , indicating the higher-order poles are not negligible [8].
, indicating the higher-order poles are not negligible [8].
The semileptonic decay branching ratio is determined by integration with respect to q2 as
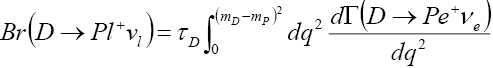 (15)
(15)
with 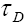 being the mean life of the D meson.
being the mean life of the D meson.
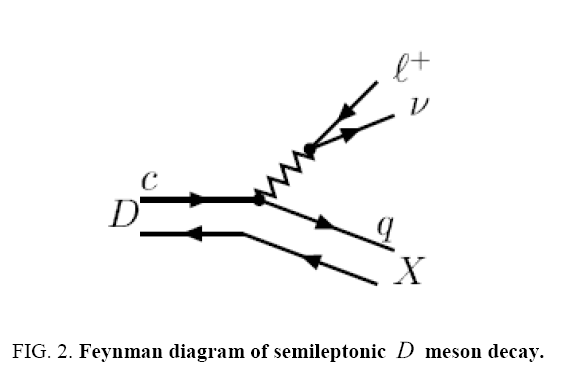
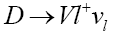 Decay:For the transitions to vector mesons, the structure of the hadronic matrix element of the process
Decay:For the transitions to vector mesons, the structure of the hadronic matrix element of the process 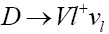 ( Figure 2), according to its Lorentz structure, is given by
( Figure 2), according to its Lorentz structure, is given by
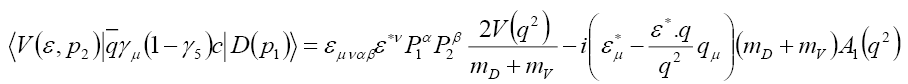
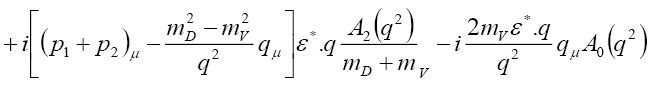 (16)
(16)
where form factors 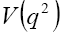 originate from
originate from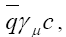 and
and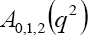 from
from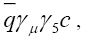 respectively.
respectively.
By decomposing equation (16) we obtain the differential and total decay rate for 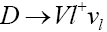 decay. Here we note that there are three polarization states namely: longitudinal and two transverse polarization states. The longitudinal polarization state differential decay rate is given by
decay. Here we note that there are three polarization states namely: longitudinal and two transverse polarization states. The longitudinal polarization state differential decay rate is given by
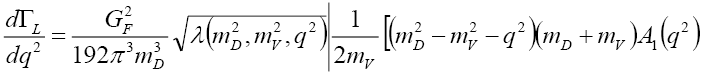
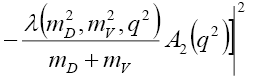 (17)
(17)
Where
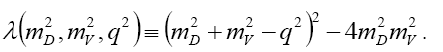 (18)
(18)
On the other hand, we obtain the differential decay rate with respect to transverse state as,
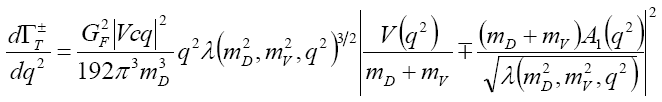 (19)
(19)
with the symbols " +"and " -"denoting the right-handed and left-handed states, respectively. We can therefore deduce from above that the combined transverse decay rate takes the form;
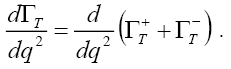 (20)
(20)
Finally, the total differential decay rate becomes
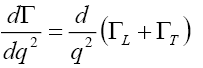 (21)
(21)
Where 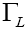 and
and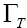 are the longitudinal and the combined transverse decay rates, respectively.
are the longitudinal and the combined transverse decay rates, respectively.
Physics Beyond the Standard Model
Physics beyond the Standard Model (BSM) refers to the theoretical developments needed to explain the deficiencies of the SM. These include aspects such as the origin of mass, the strong CP problem, neutrino oscillations, matter-antimatter asymmetry, and the nature of dark matter and dark energy [9].
Another problem lies in the mathematical framework of the SM itself due to the fact that the SM is inconsistent with that of general relativity, to the point that one or both theories break down under certain conditions, for example, within known space-time singularities like the Big Bang and black hole event horizons.
The SM is inherently an incomplete theory. There are fundamental physical phenomena in nature that the SM does not adequately explain. The first area involves phenomena not explained which include gravity, dark matter and dark energy, neutrino masses, and matter-antimatter asymmetry. Secondly, most theoretical predictions have not been observed up to date.
The Effective Lagrangian and Decay Amplitude
The most general effective Lagrangian for 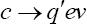 in presence of New Physics (NP), where
in presence of New Physics (NP), where 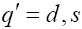 can be written as [10,11]
can be written as [10,11]
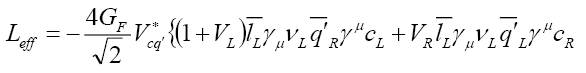
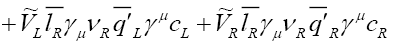
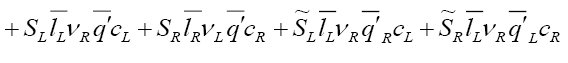
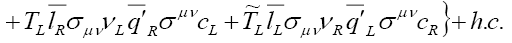 (22)
(22)
where GF is the Fermi constant, 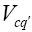 is the relevant CKM Matrix element, and
is the relevant CKM Matrix element, and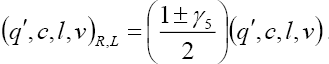 The NP couplings denoted by
The NP couplings denoted by 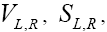 and
and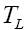 involve left-handed neutrinos, whereas, those denoted by
involve left-handed neutrinos, whereas, those denoted by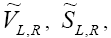 and
and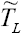 involve right-handed neutrinos. We assume the NP couplings to be real in our analysis. The projection operators are given by
involve right-handed neutrinos. We assume the NP couplings to be real in our analysis. The projection operators are given by 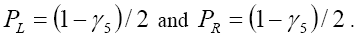 Furthermore, we neglect the NP effects coming from the tensor couplings
Furthermore, we neglect the NP effects coming from the tensor couplings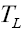 and
and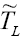 in our analysis. With this simplification, we obtain
in our analysis. With this simplification, we obtain
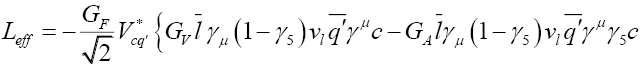
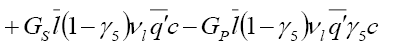
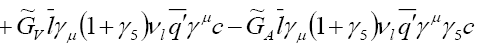
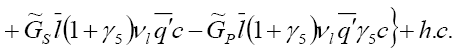 (23)
(23)
where
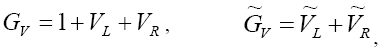


 (24)
(24)
The SM contribution can be obtained once we set 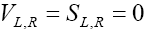 in Eq. (22) This implies that
in Eq. (22) This implies that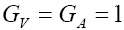 and all other NP couplings are zero. In order to compute the branching fractions and other observables for
and all other NP couplings are zero. In order to compute the branching fractions and other observables for 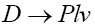 and
and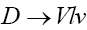 decay modes, we need to find various hadronic form factors that parametrizes the hadronic matrix elements of vector (axial vector) and scalar (pseudoscalar) currents between the initial D and final state mesons.
decay modes, we need to find various hadronic form factors that parametrizes the hadronic matrix elements of vector (axial vector) and scalar (pseudoscalar) currents between the initial D and final state mesons.
Therefore, from above, we see that expressions for 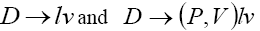 decay amplitude depends on nonperturbative hadronic matrix elements that can be expressed in terms of D meson decay constants and
decay amplitude depends on nonperturbative hadronic matrix elements that can be expressed in terms of D meson decay constants and 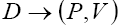 transition form factors, where P denotes a pseudoscalar meson and V a vector meson, respectively [12-15]. From the Lorentz and parity invariance we obtain
transition form factors, where P denotes a pseudoscalar meson and V a vector meson, respectively [12-15]. From the Lorentz and parity invariance we obtain
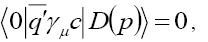
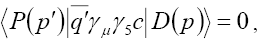
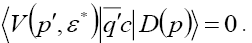 (25)
(25)
To find the scalar and pseudoscalar matrix elements, we use the equation of motion and thus we have
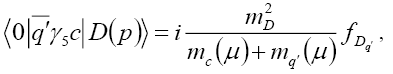
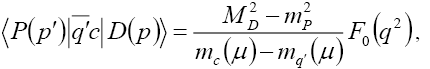
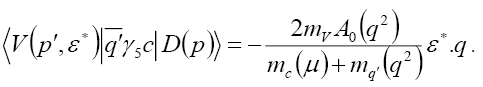 (26)
(26)
Decay Widths
Finally, using the effective Lagrangian of Eq. (23) in the presence of NP, we are capable of computing the partial decay widths of  and
and beyond the SM.
beyond the SM.
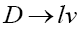
In the case of leptonic decay in the presence of NP, starting with Eq. (23) we arrive at
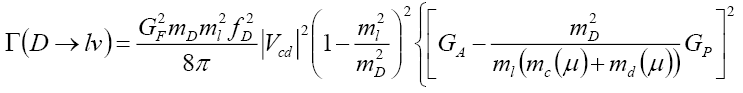
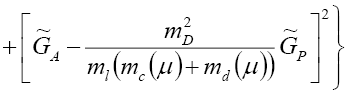 (27)
(27)
where, in the SM, we have 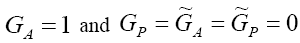 , so that we have
, so that we have
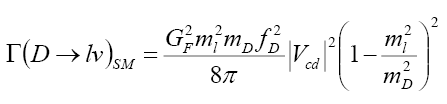 (28)
(28)
At this point, it is important to note that the right-handed neutrino couplings denoted by 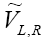 and
and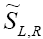 appear in the decay width quadratically, whereas, the left-handed neutrino couplings denoted by
appear in the decay width quadratically, whereas, the left-handed neutrino couplings denoted by 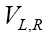 and
and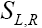 appear linearly. The linear dependence, arising due to the interference between the SM couplings and the NP couplings, is suppressed for the righthanded neutrino couplings as it is proportional to a small factor
appear linearly. The linear dependence, arising due to the interference between the SM couplings and the NP couplings, is suppressed for the righthanded neutrino couplings as it is proportional to a small factor 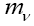 and hence is neglected.
and hence is neglected.
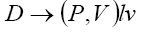
Let us now proceed to discuss the 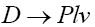 and
and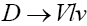 decays. In this section, we follow the helicity method of Refs. [16,17] for the semileptonic B meson decays and apply it to our case of the Dmeson decays. Therefore, the differential decay distribution can be written as
decays. In this section, we follow the helicity method of Refs. [16,17] for the semileptonic B meson decays and apply it to our case of the Dmeson decays. Therefore, the differential decay distribution can be written as
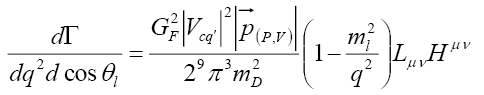 (29)
(29)
where 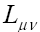 and
and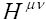 are the usual leptonic and hadronic tensors, respectively.
are the usual leptonic and hadronic tensors, respectively.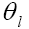 is the angle between P(V) meson and the lepton three momentum vector in the
is the angle between P(V) meson and the lepton three momentum vector in the 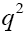 rest frame. The three-momentum vector
rest frame. The three-momentum vector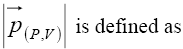
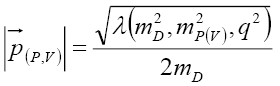
where
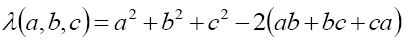 (31)
(31)
Furthermore, the differential decay distribution for 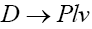 in terms of helicity amplitudes
in terms of helicity amplitudes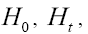 and
and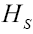 is given by
is given by
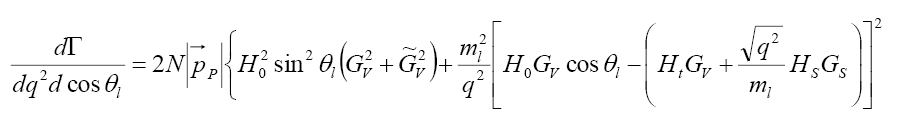
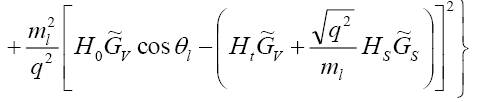 (32)
(32)
where
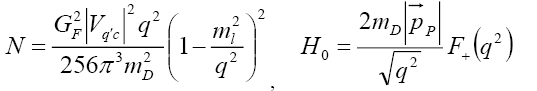
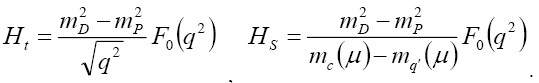 (33)
(33)
Performing the integration over 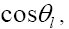 we can determine the differential decay
we can determine the differential decay 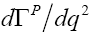 rate and arrive at
rate and arrive at
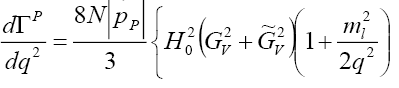
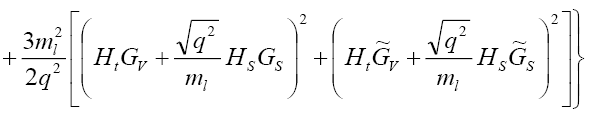 (34)
(34)
In the SM, we have ?1 V G and the rest of the NP couplings are equal to zero and henceforth we Obtain
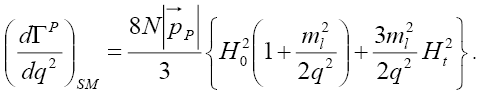 (35)
(35)
On the other hand, let us now draw our attention to the differential decay distribution for 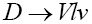 in terms of the helicity amplitudes
in terms of the helicity amplitudes 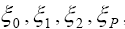 , and
, and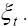 After a series of derivations, we arrive at a more simplified expression
After a series of derivations, we arrive at a more simplified expression
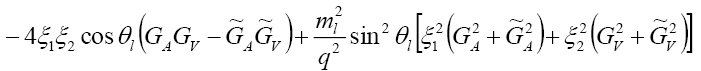
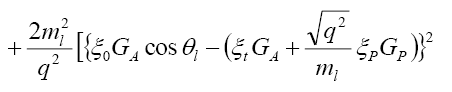
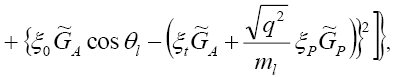 (36)
(36)
where from Eq. (36) we have
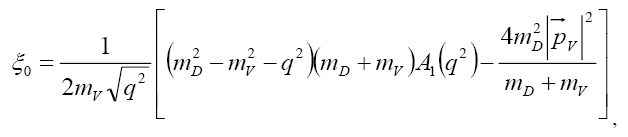
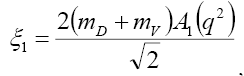
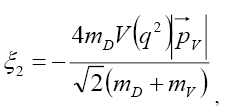
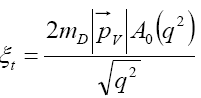
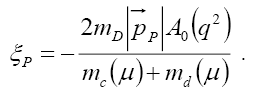 (37)
(37)
At this stage, we now perform the integration with respect to 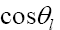 and arrive at the differential decay rate
and arrive at the differential decay rate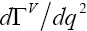 in its simplicity form given by
in its simplicity form given by
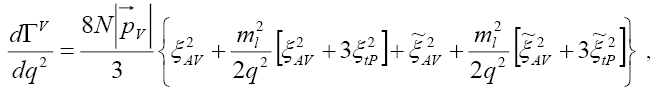 (38)
(38)
Where
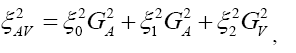
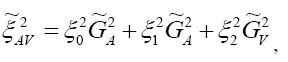
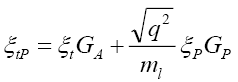
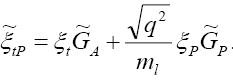
It is wise to remind ourselves at this stage that in the SM, 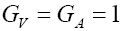 and all the other NP couplings are zero. As a result Eq. (3.17) simplifies to
and all the other NP couplings are zero. As a result Eq. (3.17) simplifies to
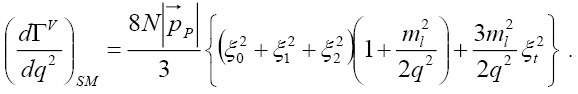 (40)
(40)
Having obtained this gigantic task of deriving the analytical results for the decay rates, we now define a very important physical observable called the differential branching ratio (DBR). This is given by
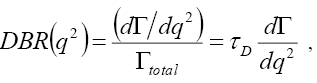 (41)
(41)
where 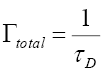 is the total decay width of D meson.
is the total decay width of D meson.
Results and Discussion
For definiteness, we first present all the inputs that are pertinent for our calculation from Ref [4]. For the quark and lepton masses we use 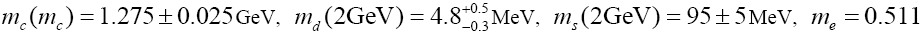
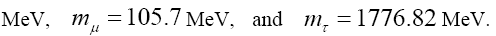 In addition, for the meson masses and lifetime we use
In addition, for the meson masses and lifetime we use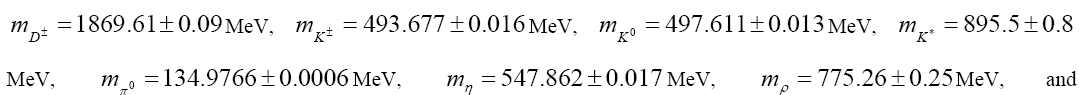
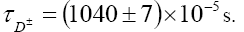
From Ref [14] we obtain the input values for decay constant and the Fermi constant as 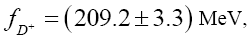
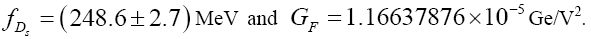 On the aspect of the CKM matrix elements, we used numerical values given in Table 1.
On the aspect of the CKM matrix elements, we used numerical values given in Table 1.
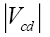 |
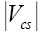 |
References |
|---|---|---|
| 0.222±0.008 | 0.986±0.016 | [14] |
Table 1: Numerical values of 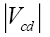 and
and 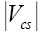 .
.
Table 2. shows some of the decay modes considered in this work and their numerical values obtained with a comparison from theory. Our results are in the same range with those obtained by other scholars who has worked in the same line of research. The differences in the numerical values may be due to variation in our input values. Secondly, differences may also be due to the process of calculating resulting from rounding off figures.
| Mode | 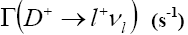 |
||
|---|---|---|---|
| This work | Decay width | Reference | |
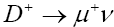 |
6.754*10-13 | 4.72*10-13 | [17] |
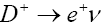 |
3.122*10-13 | 1.79*10-13 | [17] |
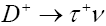 |
5.706*10-13 | - | - |
Table 2: Leptonic decay width.
From Eq. (15) we obtained the branching ratios shown in Table 3.
| Mode | This work | Branching ratio | Experiment | References |
|---|---|---|---|---|
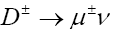 |
4.12*10-4 | (3.82±0.32±0.09)*10-4 | CLEO | [18] |
| (3.71±0.19±0.06)*10-4 | BES III | [19] | ||
| 2.2*10-4 | - | [20] | ||
| 2.87*10-4 | - | [17] | ||
| 4.3*10-3 | - | [21] | ||
| 3.82*10-4 | Exp[2] | [16] | ||
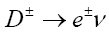 |
9.42*10-8 | <8.8*10-6 | CLEO | [18] |
| 1.0*10-8 | - | [21] | ||
| 0.5*10-8 | - | [20] | ||
| <8.8*10-6 | Exp[2] | [16] | ||
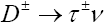 |
9.73*10-4 | <1.2*10-3 | CLEO | [18] |
| 1.5*10-3 | - | [20] | ||
| 7.54*10-4 | - | [17] | ||
| 1.05*10-3 | - | [21] | ||
| <1.2*10-3 | [2] | [16] |
Table 3: Leptonic branching ratios.
The pseudoscalar semileptonic 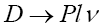 decay width for the K channel via the mode
decay width for the K channel via the mode 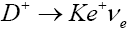 was found to be
was found to be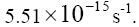 Furthermore, some comparison of the branching ratios was looked at and the numerical values obtained are under Table 4. The numerical values obtained in the SM appear to be different from experimental values as a result of computation of the decay rates as this process encompassed a good number of constants determined theoretically and experimentally.
Furthermore, some comparison of the branching ratios was looked at and the numerical values obtained are under Table 4. The numerical values obtained in the SM appear to be different from experimental values as a result of computation of the decay rates as this process encompassed a good number of constants determined theoretically and experimentally.
| Mode | This work | Experiment | References |
|---|---|---|---|
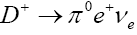 |
3.91*10-2 | (0.44±0.06±0.03)% | [15] |
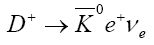 |
9.98*10-2 | (8.71±0.38±0.37)% | [15] |
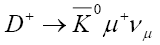 |
10.45*10-2 | (9.3±0.7)% | [4] |
Table 4: Branching ratios for 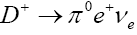 ,
,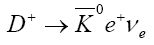 and
and 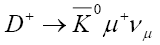
There are other  to pseudoscalar semileptonic decay channels which deserve further studies. Our calculations and experimental measurements are listed in Table 5. The calculations under these channels were taken with different trial of different decay mode and then compared to theoretical and experimental numerical values. As clearly seen our values seem to be in the accepTable range of values numerically despite the difference being so much especially with respect to the theoretical values cited under the same Table Without much clarification, it is clear that our values are a bit nearer to experimental than theoretical values. It is vital to mention that this work did not deal much on the computation of form factors under pseudoscalar decays as well as other forms of D meson decays.
to pseudoscalar semileptonic decay channels which deserve further studies. Our calculations and experimental measurements are listed in Table 5. The calculations under these channels were taken with different trial of different decay mode and then compared to theoretical and experimental numerical values. As clearly seen our values seem to be in the accepTable range of values numerically despite the difference being so much especially with respect to the theoretical values cited under the same Table Without much clarification, it is clear that our values are a bit nearer to experimental than theoretical values. It is vital to mention that this work did not deal much on the computation of form factors under pseudoscalar decays as well as other forms of D meson decays.
| Mode | BR | BR(%) | References | |
|---|---|---|---|---|
| This work | Theoretical | Experiment | ||
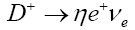 |
2.01*10-2 | 0.10 | <0.5 | [15] |
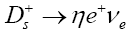 |
3.15*10-2 | 1.7 | 2.5±0.7 | [15] |
Table 5: Branching ratios for D+and Ds+to η
For the vector 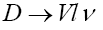 decays, we took into consideration are
decays, we took into consideration are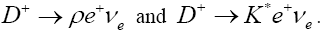 Table 6 shows a comparison of the values obtained with other theoretical values. In addition to the partial decay rates under Table 6, this work also computed total decay width for
Table 6 shows a comparison of the values obtained with other theoretical values. In addition to the partial decay rates under Table 6, this work also computed total decay width for 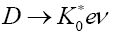 and arrived at
and arrived at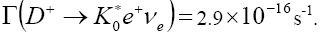 On the other hand, the branching ratio was found to be
On the other hand, the branching ratio was found to be 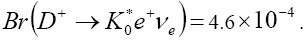
| Mode | Branching ratios | References | |
|---|---|---|---|
| This work | Theoretical | ||
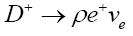 |
3.12*10-3 | 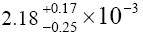 |
[4] |
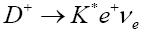 |
4.98*10-2 | (3.68±0.10)% | [4] |
Table 6: Branching ratios for 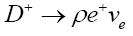 and
and 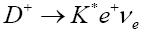
We have seen the transition from Eq. (27) to Eq. (28) via fixing of our NP couplings by assigning ? A G 1 and the rest of the couplings equal zero. The same approach applies BSM.
It is vital to note that experiments on a general view do not follow any theory hence making us check our results both from the theoretical aspect as well as experimental results. With this in mind, we now set the standard value of our NP coupling constants as per theory. The standard is usually set at 1.25 ± 0.04 where 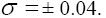
Now for our work, we needed to set the NP coupling constants in such a way as to arrive at the constraint contribution of each one of them. We began by focusing on the pure leptonic decay 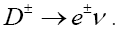 We used Eq. (27) and by setting the NP coupling constants appropriately, we checked the contribution of each. The first step was to vary A G and set the rest of the couplings to zero.
We used Eq. (27) and by setting the NP coupling constants appropriately, we checked the contribution of each. The first step was to vary A G and set the rest of the couplings to zero.
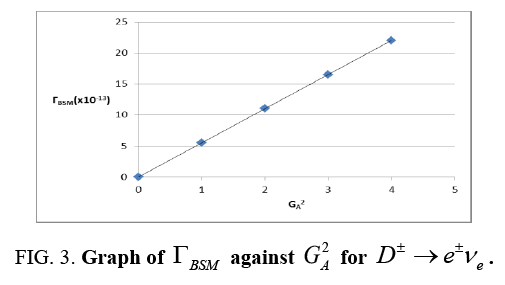
From Figure 3. we see the dependence of the decay rate BSM on the NP coupling constant 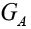 . For
. For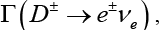 the constraint for
the constraint for 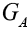 is found to be
is found to be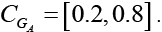 The same method was applied to the other couplings and the results were as shown in Table 7.
The same method was applied to the other couplings and the results were as shown in Table 7.
| NP coupling constant | Constraints |
|---|---|
| GA | [0.2,0.8] |
| GP | [0.9,1.4] |
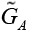 |
[0.2,0.8] |
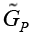 |
[0.9,1.4] |
Table 7: NP coupling constraints for leptonic decay 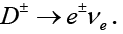
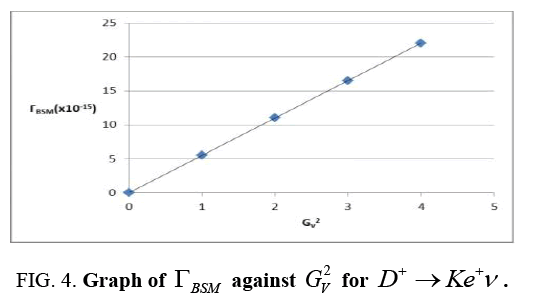
On the other hand, we looked at the pseudoscalar decay mode 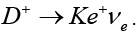 Figure 4 shows the dependence of the decay width on the NP coupling constant
Figure 4 shows the dependence of the decay width on the NP coupling constant 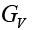 . Like-wise, this was achieving by varying
. Like-wise, this was achieving by varying 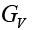 and setting the rest of the NP coupling constants to zero. Thereafter, varying each one of then and setting the rest to zero in order to attain the constraints for each constant.
and setting the rest of the NP coupling constants to zero. Thereafter, varying each one of then and setting the rest to zero in order to attain the constraints for each constant.
It was deduced that the constraint for 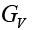 is
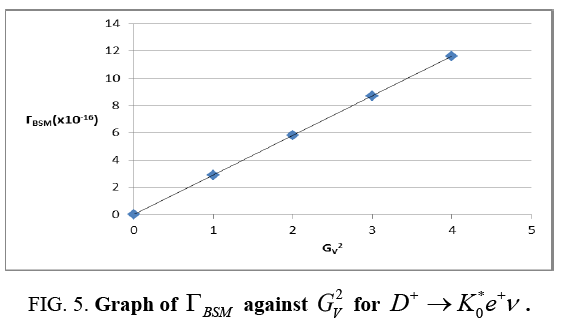
is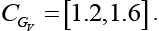 The contribution of the rest of the couplings are shown in Table 8. Finally, we considered the decay mode
The contribution of the rest of the couplings are shown in Table 8. Finally, we considered the decay mode 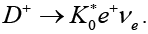 The dependence of the decay width on
The dependence of the decay width on 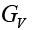 is shown in Figure 5.
is shown in Figure 5.
| NP coupling constant | Constraints |
|---|---|
| Gv | [1.2,1.6] |
| GS | [1.3,1.8] |
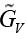 |
[1.1,1.7] |
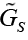 |
[0.8,1.5] |
Table 8: NP coupling constraints for pseudoscalar decay 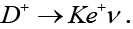
The constraint for 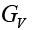 were estimated to be
were estimated to be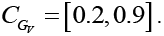 The rest of the constraints for the other couplings are shown in Table 9.
The rest of the constraints for the other couplings are shown in Table 9.
| NP coupling constant | Constraints |
|---|---|
| GV | [0.2,0.9] |
| GA | [0.5,1.6] |
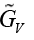 |
[0.6,1.2] |
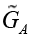 |
[0.3,1.4] |
Table 9: NP coupling constraints for vector decay 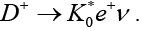
Conclusion
The leptonic, pseudoscalar and vector decays have been studied under this work with the aid of the effective Lagrangian by including the allowed direct NP couplings. Charm decays has been and still is an exciting field for both theoretical and experimental investigations. Charm quark transition amplitudes, described in this work, represent a crucial tool to understand strong interaction dynamics in the non-perturbative regime. Complementary information that constrains model building and lattice gauge calculations is coming from the rich spectroscopy of charmed mesons and baryons, which is beyond the scope of this paper.
Coming to our results, we see from our results that more needs to be done in order to understand the real phenomenology of physics BSM. Parameterization of decay constants into physical numerical values still remain a challenge among theorists. Nevertheless, more progress has been made in recent years to try and fuse in the gaps that the SM has left scholars with more questions than answers.
From our results, we can see that a search for NP under D meson decay is equally important as well as that of the B meson. The results obtained under this work do not entail pure accuracy as earlier on mentioned as they are equally prone to errors just like those from experiments too.
Acknowledgment
I also wish to thank all the Professors that taught me during the course of my study for their guidance, support, and their efforts to teach and equip me for this task. I wish to thank Professor Xin-Qiang Li for his expertise in the field and his advice there on.
References
- Oerter R. The theory of almost everything: The standard model, the unsungtriumph of modern physics (Kindle ed.). Penguin Group. 2006:2.
- Barbier R, Berat C, Besancon M, et al.R-parity violating supersymmetry. Phys Rept. 2005;1:420.
- WuCS. Experimental test of parity conservation in beta decay. PhysRev. 1957;105:1413-15.
- Olive KA. (Particle Data Group), Chin Phys. 2014; C38 090001(URL: http://pdg.lbl.gov).
- Hitlin D. D Meson Decay Studies at the ψ. Pasadena, California 91125. 1984
- Richman JD, BurchatPR. Rev Mod Phys. 1995;67:893.
- Petrov AR, Alexey A. Hadronic D and Ds mesondecays. Rev Mod Phys. 2012;84:65
- Davies CTH, McNeile C, Follana E, et al.Rapid Communications. Phys RevD. 2010;82:114504
- Pati JC, Salam A. Phys. "Natural" left-right symmetry. Rev Lett. 1973;31:661.
- Bhattacharya T, Cirigliano V, Cohen SD, et al. New precision measurements of free neutron beta decay with cold neutrons. Phys RevD. 2012;85:054512.
- Cirigliano V, Jenkins JM, Gonzalez A. Chiral effective theory methods and their application to the structure of hadrons from lattice QCD. Nucl Phys. 2010;830:95.
- Korner JG,SchulerGA.Exclusive semileptonic heavy meson decays including lepton mass effectsZ. Phys C. 1990;46:93.
- Kadeer A, Korner JG, MoosbruggerU.Helicity analysis of semileptonic hyperon decays including lepton-mass effects. Eur Phys J C. 2009;59:27.
- Sezione di TV. FLAG: Lattice QCD tests of the standard model and forestate for beyond. University of Rome. I-00133 Rome. 2015;6:45
- Ma HL, Rong G, Yang YD. Leptonic Semileptonic D(Ds)decays and CKM matrix. 2014
- Alexander JP, Cassel DG, DuboscqJE, et al. CLEO Collab Phys Re.2009;79:52001.
- Artuso M.CLEO Collab Phys Rev Lett. 2007;99:071802.
- Hakan C, Huseyin K. Meson decay in an independent quark model. Int J Mod Phys. E9;2000:407.
- Eisenstein BI. (CLEO Collaboration). Phys Rev. 2008;78:052003.
- Ablikin M. (BES III Collaboration). Phys Rev. 2014;89:51104.
- Bhavin P, Vinodkumar PC. Decay properties of D and Ds mesons in coulomb pluspower potential (CPP). Chin Phys. 2010;34:1497.
- Wirbel M, Bauer SB.Evidence of New States Decaying into Ξ*cπ Z. Phys. 1985;29:637.
 against
against for
for
 for
for 
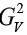 for
for