Review

, Volume: 7( 1) DOI: 10.37532/2320-6756.2019.7(1).174

• View PDF
• Download PDF

Beyond Einstein’s Special Theory of Relativity

*Correspondence:

Theodore G Pavlopoulos Physicist, USA, Tel: 541-505-8089; E-Mail: ted.pavlopoulos@gmail.com

Abstract

Quantum mechanics and the Special Theory of Relativity (STR) are the cornerstones of modern physics. For some time, however, researchers have argued that these theories are either individually or jointly incomplete. For instance, they do not provide a means for calculating the masses of elementary particles, such as the electron, proton, and neutron. Here, we assume that STR is only an approximation, which thus require an extension. The extended theory proposed requires high-energy electromagnetic radiation, such as gamma-rays, to propagate superluminally, as recent astronomical observations suggest. These gamma-ray-bursts are characterized by hartto-soft spectral evolution.

Keywords

Gamma-ray bursts; Superluminal velocities for gamma-rays; Lorentz violation; space travel

Introduction

While monitoring the nuclear test ban treaty, Gamma-Ray Bursts (GRBs) were first observed by the Vela military satellite during 1969-1971 and were first reported in the literature in 1973. GRBs are sudden and intense flashes of gamma rays, which, for a few seconds, outshine all other astronomical sources. Gamma-rays have been observed to last for only a few seconds, but more often take the form of strings of pulses that last up to 1000 seconds. This long duration of GRBs requires an explanation. Gamma-rays are travel billions of light years to reach earth. The energy of GRBs ranges from a few keV to several MeV. According to the STR, all electromagnetic radiation, regardless of wavelength (energy), should travel at the same speed “c.” Hence, we should observe the shape of GRBs as they first originated. However, this is not the case. As gamma-rays travel cosmic distances, they follow a hard-to-soft spectral evolution pattern. The hardest (highest-energy) gamma-rays in the burst will separate from the softest (lowest-energy) gamma rays and arrive first, followed by the lower-energy rays, X-rays, and an afterglow. In their publication, the authors Deng and Zhang state that this hard-to-soft evolution pattern of gamma rays fourteen times [1]. The authors state that “…the widely-observed hard-to-soft Ep evolution across broad pulses cannot be accounted for unless a contrived condition is invoked.” Time lags are common in GRBs and the time lag Δt will increase with distance (time) traveled (positive time-lags).

Pavlopoulos [2], was the first to predict superluminal velocities for gamma-rays. Further, Pavlopoulos explained the hard-tosoft pattern observed as Lorentz violation [3]. Negative time lags have also been observed in GRBs. In these cases, the time lag between the leading gamma-ray pulse and the second pulse of higher energy decreases with the time of travel. Pavlopoulos [3] also explained as Lorentz violation.

Methodology

New physics

• This hyperbolic wave equation (1) describes almost all electrodynamics:

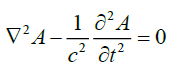(1)

The Lorentz transformation leaves equation (1) invariant. The static, spherically symmetrical case (2A=0) has the following solution:

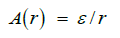(2)

This is an undesirable solution because, for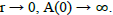

• This means that an electron should explode. This suggests that equation (1) needs to be expended

According to Heisenberg [4], any theory that can be used to calculate the masses of elementary particles must contain a constant with the dimension of length (ℓ₀). This follows from dimensional considerations. With de Broglie’s relation, with p standing for impulse and λ for wavelength.

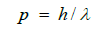(3)

As dimensions for the impulse, we have p=mc=h/ℓ₀ and m=h/cℓ₀. Here, we face an interesting question: c and h are universal constants, and both are Lorentz invariants, but the length ℓ₀ is not [5]. This leads to the following speculation: Is equation (1) only an approximation? How can one construct an extended version of the STR that also contains ℓ₀ as a second universal constant in addition to c? Furthermore, such an equation should reduce to the STR for ℓ₀ → 0. Pavlopoulos [2], proposed a theory that extended the STR. In addition to c, the extended theory contains a length ℓ₀ as a second universal constant.

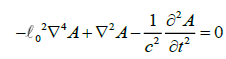(4)

This theory predicts superluminal velocities for gamma-rays.

With the “ansatz” A=A0 e^i(ωt+kx), one obtains from the equation (4) the dispersion relation

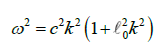(5)

and the signal (group) velocity v_gr,

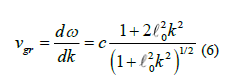
For 1 >> ℓ₀²k², we obtain

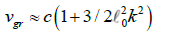(7)

Contrary to the STR, very short electromagnetic waves (gamma-rays) propagate faster than the speed of light c.

New Observations of Gamma-Ray Bursts

• The major result of the study by Chincarini et al. [5], is that: “Every flare seems to have a memory of the previous events so that as time progresses, each flare is weaker and softer than the preceding one.” This finding suggests a Lorentz violation. Furthermore, the hard-to-soft evolution is a strong indication that X-ray flares and gamma-ray pulses have a common origin. According to the abstract by Margutti et al. [6], whatever produces each X-ray flare keeps a memory of the GRB’s history, starting from the prompt emission. This result, together with the related work on early time flares, provides a set of clear observational properties that every model aims to explain. In addition, according to Margutti [7], there is direct evidence that gamma rays, X-rays, and lower-energy radiation are produced by the same mechanism. This suggests that whichever mechanism is at work in the gamma-ray prompt emission may also be the source of the X-ray flare emission hundreds of seconds later. This lag-luminosity relationship has been proven to be a fundamental law extending ~5 decades in energy and ~5 decades in time. Again, this suggests Lorentz violation

• Hakkila and Preece [8], made the following observation: “The large degree of similar spectro-temporal behavior within GRB indicates that a single process is responsible for producing pulses spanning a tremendous range of durations, luminosities, and spectral hardness.” Here, we propose this process is produced by Lorentz violation. Further, these authors claim that the most difficult issue affecting GRB pulse fitting is the confusion caused by overlapping pulses. This can also be explained by invoking Lorentz violation. Here, a higher energy pulse catches up with the lower energy pulse (negative time leg) and overlapping it

• It was noted by Hakkila et al. [9], that empirical approaches demonstrate that GRB pulse light curves can be generally presented by a hard-to-soft spectral evolution. Pulses are generally hardest at the first instant they appear, and they continue to soften during the pulse rise, past the pulse peak, and through the pulse decay. And continue: “We note the rather remarkable result that the hardness evolution seems to differ for hard pulses and soft pulses. Specifically, hard pulses seem more likely to evolve hard-to-soft, while soft pulses are less likely to show this behavior.” Again, this can be explained by Lorentz violation. Hard gamma-rays obey equation (4), while longer wavelength electromagnetic radiation can still be presented with equation (1)-the STR

• According to Broadbent [10], “Hard-to-soft spectral evolution is so central to the GRB pulse structure that it can be used as a defining characteristic in rigorous statistical modeling techniques. The harder a pulse is, the more pronounced the evolution typically is”

• Sanchez et al. [11], investigated the effects of the Lorentz invariance violation and aimed to determine the distance to PG 1553+113, an astronomical object in the Serpens Caput constellation that emits high-energy radiation in the 100 MeV<E<300 GeV range. The goal of their study was to put constraints on possible Lorentz invariance violations manifesting as the energy dependence of the velocity of light in vacuum and to set limits on the energy scale at which quantum gravity effects causing Lorentz invariance violation. The authors firstly examined non-zero dispersion parameters like time separation and for the energy parameters such as of these flares to determine the distance of PG1553+113 without using optical (redshift) measurements. Significantly, after optical data were used, a good agreement between the two distance measurements was obtained. This is an important observation. Astronomical distance measurements without optical redshift measurements are only possible if dispersion (Lorentz violation) is present

• Summary: (a) Hard-and-soft gamma rays, X-rays, and longer wavelength radiation are all generated and emitted about the same time over a short time interval. After traveling over cosmological distances, we observe a hard-to-soft energy development. These observations are difficult to explain without implying Lorentz violation (b) Furthermore, recent years, have seen several publications carrying titles such as “Long GRBs as Standard Candles?” This is possible only if gamma rays undergo dispersion during their long travel through space. Thus, this entails Lorentz violation

Superluminal Velocities and Space Travel

The history of space exploration began when the Russians successfully launched the Sputnik 1 satellite in October 1957. The first U.S. Moon landings took place on July 20, 1969. By this time, a large part of the world’s population had become space-flight enthusiasts. The public then became aware that Venus and Mars might be also reachable, however, it was understood that considerable length time to reach these two planets. Rocket-propulsion systems could only propel spacecraft to speeds of about 20,000 km/hr. Parallel to the early successes in space, the prospect that other Earth-like planets harboring life may exist further ignited humankind’s fantasy. Our galaxy, the Milky Way, contains billions of stars, and a certain percentage of these stars (suns) should have planets orbiting them. Further, besides our Milky Way, there are also billions of galaxies in the universe. This increases the probability of human-like beings inhabiting planets exponentially. Unfortunately, the unimaginable distances between our solar system and others and the relative brevity of a human’s lifetime seem to present insurmountable obstacles to space travel. Although light travels 300,000 km per second, Alpha Centauri is about 4.4 light-years away. The only solution to this challenge would be to be to have the ability to travel at superluminal speeds. However, a real challenge seems to have been overlooked by many space-enthusiasts. Following the above-described approach, a spacecraft would have to reach the speed of light c, and then surpass c to reach superluminal velocities. Thus, ignoring the problem of the propulsion system being able to reach the speed of light c, superluminal velocities are not possible according to Einstein’s STR. Nothing can move faster than the speed of light c. The spacecraft seen in Star Wars and Star Trek must have been able to travel faster than the speed of light c in order to bridge the unimaginable distances separating stars positioned in different galaxies. Significantly, if gamma-rays can travel at superluminal speeds, it should also be possible to accelerate a mass (a spaceship) to superluminal velocities, which is a very exciting finding for humankind, as it will create a realistic possibility of future space travel (exploration).

Acknowledgment

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

References

1. Deng W, B Zhang. Cosmological implications of fast radio burst/gamma-ray burst associations. ApJL. 2014;785:15.
2. Pavlopoulos TG. Breakdown of lorentz invariance. Phys Rev. 1967;159:1106.
3. Pavlopoulos TG. Are we observing Lorentz violation in gamma-ray bursts? Phys Lett B. 2005;625:13-18.
4. Heisenberg W. About the universal length occurring in the theory of elementary particles. Ann Phys. 1938;32:20.
5. Chincarini G, Mao J, Margutti R, et al. Unveiling the origin of X-ray flares in gamma-ray bursts. MNRAS. 2010;406:2113-48.
6. Margutti R, Guidorzi C, Chincarini G, et al. Lag-luminosity relation in γ -ray burst X-ray flares: a direct link to the prompt emission. MNRAS. 2010;406:2149-67.
7. Margutti R. Lag‐luminosity relation in gamma‐ray burst X‐ray flares. 2010;1279:372.
8. Hakkila J, Preece RD. Gamma-ray burst pulse shapes: evidence for embedded shock signatures? ApJ. 2014;783:88.
9. Hakkila J, Lien A, Sakamoto T, et al.Swift observations of gamma-ray burst pulse shapes: grb pulse spectral evolution clarified. ApJ. 2015;815:134.
10. Broadbent MF. 2014 Ph.D. Thesis
11. Sanchez DA, Brun F, Couturier C, et al. Probe of lorentz invariance violation effects and determination of the distance of PG 1553+113.