Research
, Volume: 11( 1) DOI: 10.37532/2320-6756.2023.11(1).315A Possible Role of the Energetically Excited Quantum Vacuum in Cosmology: A Potential Solution to the Horizon and Flatness Problems- The Excitation Energy Dominated Era
Received date: 09-January-2023, Manuscript No. tspa-23-86173; Editor assigned: 10-January-2023, PreQC No. tspa-23-86173 (PQ); Reviewed: 12-January-2023, QC No. tspa-23-77938 (Q); Revised: 13-January-2023, Manuscript No. tspa-23-86173 (R); Published: 21- January-2023, DOI. 10.37532/2320-6756.2023.11(1).315
Citation: Marosi L.A. A Possible Role of the Energetically Excited Quantum Vacuum in Cosmology: A Potential Solution to the Horizon and Flatness Problems–The Excitation Energy Dominated Era.2023;11(1):315.
Abstract
The cosmological model presented here rests on the postulate that the universe can be described as an interacting attraction (exerted by matter) and repulsion (exerted by the excitation energy of the quantum vacuum) system in viral equilibrium. The basic parameters of the model, the matter density and the excitation energy of the quantum vacuum are determined by observations and are not adjusted to the model. The model requires only a few assumptions that can be deduced from the laws of conventional physics and from the rules of quantum field theory. Existing problems in standard cosmology, such as the flatness and the horizon problems, among others, can be resolved in a straightforward way without inflation and without recourse to dark matter and dark energy.
Keywords
Flatness problem; Horizon problem; Cosmic microwave background anisotropy; Isothermization; Thermalization
Introduction
Development of the ΛCDM cosmological model
In 1917 Einstein applied his theory of general relativity (GR) to the universe as a whole, and found the surprisingly simple solution [1]:

Equation (1) describes an expanding universe, where the expansion velocity v is a function of the mass density ρM.
Einstein believed in a static universe and accepted the expanding universe hypothesis only in 1929 after Hubble published his famous “relation between distance and radial velocity among extra-galactic nebulae” [2]

which is usually expressed as a redshift-velocity law:

where z is the redshift, v is the expansion velocity, c is the speed of light, H0 is Hubble’s constant and d is the co-moving distance of the emitting object.
In 1931 the Einstein–deSitter (EdeS) model of an expanding universe was developed and this became the standard model of the universe for many decades [3].

This model describes a flat universe expanding with velocity Ht, with a critical density ΩM = ρcr, and curvature term k = 0.
Due to the difficulty in finding detectible amount of intergalactic matter and subluminous stellar objects etc., direct observation of the matter density is difficult. With a firm belief in the velocity interpretation of H0, the argument and the function value in Equation 1 were exchanged as follows:

with serious consequences for the further development of the cosmological model. A number of fatal contradictions arose between observation and the predictions of the theory such as the missing mass and age problems. The Lambda Cold Dark Matter (ΛCDM) model, which contains variable amounts of Dark Matter (DM) and Dark Energy (DE) and a fixed value of H0, was devised in order to make the model compatible with observations. The dynamic of the universe can be described by the Friedman Equation [4].

where a is the scale factor, Λ is Einstein’s cosmological constant, ρM is the mass density containing both luminous and dark matter and k can take the values +1, -1, or 0 for representing a closed, open, or flat universe, respectively.
Convinced by the ‘three evidences of proof’, i.e., the existence of the Cosmic Microwave Background (CMB), the Big Bang Nucleosynthesis (BBN) and the Hubble Law and in view of the excellent agreement between the concordance model and astronomical observations the majority of astronomers believe that the ΛCDM model is a correct description of the beginning and evolution of the universe.
Objections against the ΛCDM model
Despite its great success for explaining cosmological and astronomical observations we should bear in mind that the ΛCDM model consists of a large number of unexplained and in partially unprovable hypotheses such as the still elusive DM and dark energy DE, negative pressure, the actual tiny value of the cosmological constant, and the redshifts (RS) of spectral lines emitted by distant galaxies is due to expansion, among others.
It is important to note that in its present form the ΛCDM model is incomplete in that without pre-BB fine–tuning it cannot explain the horizon and flatness problems on its own. These problems were solved by inflation as put forward by Guth 1981 [5]. The inflationary theory, however, is not generally accepted. In order to work inflation requires a pre-inflationary fine tuning of the initial conditions in order of 10-15, every other number would lead to “bad inflation” [6]. In addition to this, the theory is based on a number of subsequent, mutually substantiating hypotheses and assumptions without profound physical basis. For these reasons inflation is object to serious criticism [7–10]. Dispensing with inflation, however, would mean that the fine-tuning and horizon problems cannot be explained within the standard model and this shortfall remains an unsolved conundrum of current cosmology.
The Hubble constant dilemma
The problem with the Hubble constant is twofold. Firstly, redshift from local measurements (calculated from the redshift of spectral lines emitted by distant galaxies) and redshift from global measurements (calculated from the CMB power spectrum) lead to different results: h=72-73 as compared to h=67.8 (h=(km s-1 Mpc-1)/100). The problem is that the error bars of these two independent measurements do not overlap. The significant difference between the local and global measurements is taken so seriously that the need for new physics beyond the current standard model has been discussed in order to explain this discrepancy [11, 12].
Secondly, it was demonstrated that simpler EdeS models with zero cosmological constant fit the CMB power spectrum as well as,
or even better, than the concordance model [13, 14]. The calculation of h from various EdeS models without the cosmological
constant leads to a substantially lower value of 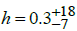 [13]. A Hubble constant of h=0.3 is completely inconsistent with h ~ 0.7
and attempts to bring together these two values have been unpromising. Both values cannot mean expansion and hence the
possibility has been considered that the RS of the spectral lines and the RS derived from the CMB may have different physical
origins [15]. This idea may appear controversial, but the Hubble Diagram (HD) tests suggest that this reasoning is correct.
[13]. A Hubble constant of h=0.3 is completely inconsistent with h ~ 0.7
and attempts to bring together these two values have been unpromising. Both values cannot mean expansion and hence the
possibility has been considered that the RS of the spectral lines and the RS derived from the CMB may have different physical
origins [15]. This idea may appear controversial, but the Hubble Diagram (HD) tests suggest that this reasoning is correct.
• The representation of the shape of the HD in the more sensitive linear d/z instead on the strongly dumped logarithmic μ/z scale in the RS range of 0.0104–8.1 does not follow the prediction of the ΛCDM model but clearly shows an exponential slope that is characteristic for energy decay with a constant rate [16-19].
• In contrast to the global-scale isotropic and homogeneous CMB radiation in thermal equilibrium, starlight is a local property of the vacuum, far away from the thermal equilibrium, that, expectedly, as every excited quantum mechanical system, has the tendency to roll down towards the energy equilibrium state, that is the Planckian-type black-body radiation. This process means there is no loss of energy, but only an energy transfer of starlight into the equilibrium blackbody radiation and the law of energy conservation is not violated. In this case the RS of the starlight does not represent the velocity of expansion (in km s-1 Mpc-1), but the velocity of thermalizaton (in kHz s-1 3.08×1024Hz-1). For convenience, the energy loss by thermalization is expressed in the numerical range of the velocity interpretation.
• There are further reasons to consider the case that the value of h=0.3 could be the right one. Various tests based on observational data have been performed to provide evidence for the expansion hypothesis, and the results show that static universe models fit the observational data better than the ΛCDM model [20-29]. It is important to point up that within measurement errors, slowly expanding universe models are also compatible with the results of the expansion tests, and hence should not be excluded from further considerations [30].
Aim
The large number of hypothetical objects and unprovable hypotheses raises legitimate doubts about the validity of the underlying ΛCDM theory, and suggest the need for alternative theories that can account for cosmological observations without DM and/or DE and without resorting to unprovable hypotheses. In recent years a number of papers have appeared in the literature explaining CMB anisotropy, flat rotation curves of galaxies and further astronomical observations as well as proposals of new universe models without DM or DE or both [14, 31-45].
The present paper is an attempt to investigate if alternative models based only on forms of matter and the Excitation Energy of the Quantum Vacuum (EEQV) above the ground energy state, which is equivalent to the energy of the CMB photons contained, and known to be present in the universe, could explain astronomical observations without invoking improvable constituents and hypotheses. I will show that models based on ordinary matter and EEQV can explain the flatness and the horizon problems, the energy conservation problem of the red shifted radiation and the BBN.
The EEQV Governed Cosmological Model-Basic Postulates
Postulate 1
The presented cosmological model (abbreviated as the PB model in the following discussion) rests on the basic postulate that the universe can be described as an interaction attraction (exerted by matter, baryons (B)) and repulsion (exerted by the excitation energy of the quantum vacuum (P)) in a virial equilibrium.
Postulate 2
The Excitation Energy of the Quantum Vacuum (EEQV), i.e., the energy of excitation above the ground energy state, is represented by the energy of the Photons (P) contained in the universe.
Supporting line of reasoning:
• A vacuum is thought of as an entity of dynamical, intimately interacting quantum fields filled with virtual particles that are in continuous energy fluctuation according to Heisenberg’s uncertainty principle. Photons are the dominant virtual particles and can be interpreted as elementary excitations of interacting quantum fields, where the energy of the photons represents the measure of the excitation energy above the ground energy state.
• Empty space possesses a repulsive force that expands space. The existence of a repulsive force working in the universe is a generally accepted hypothesis and supported by astronomical observations [46-48]. For example, the peculiar velocities of galaxies on the surface of empty spaces (voids) reveal an unexplained, additional velocity component: the empty or lessdense region inside voids expands faster than the background, due to the suspected Hubble flow. Whereas regular energy and matter always attract other energy and matter, the empty space repels [49]. This special feature of void expansion leads to the conclusion that the energy of empty space must be repulsive. The physical nature of this force, however, is unknown. The most widely accepted hypothesis is that DE, the energy of the QV, is the source of this energy, and, thus, the repulsive force is a property of empty space itself. However, the discrepancy between the vacuum energy calculated from quantum field theory and the observed vacuum energy from cosmology exceeds the observed value by some 120 orders of magnitude. This result suggests that the energy of the vacuum cannot account for the low actual value of the cosmological constant.
• In the following discussion I assume that it is not the almost infinite energy of the QV but only the excitation energy above the ground energy state represents the cosmological constant. In contrast to the constant energy density of the true vacuum, which exists at a global minimum state and unlike the constant energy density of the false vacuum, which exists at a local minimum of energy and hence exerts a negative pressure, the EEQV does not represent a minimum energy, and in the same way as every excited quantum mechanical system its energy has the tendency to decrease towards the ground energy state. According to conventional physics, the EEQV will exert a positive pressure, i.e., a repulsive force, which is equal to the excitation energy density.

The most natural way for the excitation energy to decrease is through the expansion of space, acting against the gravitational attraction of the baryons, and this expansion is accompanied by an equivalent RS.
Notes on postulates (1) and (2): The repulsive force of the EEQV, expressed by the energy of the photons, is to be seen as an inherent property of the excited QV–light entity itself and must not be confused with the mechanical nature of radiation pressure exerted upon any surface exposed to electromagnetic radiation, where individual photons are pushing on something substantial.
The Attraction, Repulsion Governed Universe
Marosi was the first to point out the striking fact that the total energy of the CMB contained in the universe has a value close to the gravitational energy GM2 /R, i.e. [39, 40],

MU is the total mass contained in the universe, RU is the radius of the universe and the subscript U is an abbreviation for Universe. In Equation (8) the attractive gravitational force of baryons is balanced by the repulsive force of the EEQV (expressed by the energy of the CMB) rather than by the kinetic energy of expansion.
The radius RU of a flat universe with 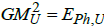 can be inferred from,
can be inferred from,
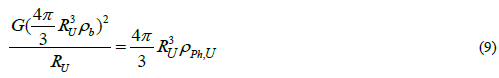
To give,

In Equations (9) and (10) ρB is the baryon mass density, ρPh the energy density of the photons and RU the radius of the universe. The cosmological parameters used for these calculations and the results for the different mass densities are shown in TABLE 1 and TABLE 2.
TABLE 1. Cosmological parameters used for calculation.
| Parameter | Accepted range |
|---|---|
| Nphoton cm-3 | 413 |
| Ephoton ergs cm-3 | 4.2×10-13 |
| Ρbaryon g cm-3×10-31 | Broad: 1.0 - 5; sensible: 1.7-4.1 |
| NB/NPh×10-10 | 2.5 - 6 |
| Energy photon/particle (ergs) | 1.017×10-15 |
TABLE 2. Parameters calculated using the values in TABLE 1.
| ρB, g cm-3×10-31 | 1 | 1.7 | 2 | 3 | 4 | 5 |
| Ru (cm × 1028 ) | 1.22 | 0.71 | 0.6 | 0.41 | 0.3 | 0.24 |
| MU (g×1053) | 77.1514 | 15.7035 | 9.64392 | 2.85746 | 1.20549 | 0.61721 |
| NB/NPh×10-10 | 1.43 | 2.43 | 2.85 | 4.29 | 5.71 | 7.14 |
| H0 km s
|
7.28 | 9.49 | 10.29 | 12.6 | 14.55 | 16.27 |
It is indeed puzzling that the radius of the universe as inferred from Equation (10) roughly corresponds with the radius of the visible universe calculated on basis of the ΛCDM model.
Basic Equations: A Return to Einstein’s Repulsive Force
In its simplest form, general relativity predicts that the universe must either expand or contract. Einstein thought the universe was static, so he added a repulsive term (the cosmological constant Λ) to the theory of general relativity in order to and obtain a static solution. In Einstein’s original idea, the cosmological constant represented a repulsive force counterbalancing the attractive force of gravitation.
Einstein assigned the cosmological constant Λ to the left-hand side of Equation (11) which represents the geometrical part of the gravitational field,
In Equation (11) Rik is the Ricci tensor, Rgik is the Ricci scalar, Tik is the matter tensor and Λ is Einstein’s cosmological constant.
This stands in contradiction to the currently preferred interpretation of the matter tensor according to every form of energy, including the energy of the quantum vacuum, that contributes to gravitation is thus part of the matter tensor [50].
My interpretation, however, is not entirely arbitrary, since it is completely consistent with Einstein’s original reasoning. Since GR never defined the exact nature of matter both interpretations of the matter tensor could turn out to be more successful when applying GR to the universe as a whole. Observations and experiments are needed to determine what matter means and the appropriate interpretation that generates the real world [51].
In this work I investigate the case that the cosmological constant in Equations (11) is actually a time-dependent quantity, i.e., the decaying excitation energy of the quantum vacuum,

which, similar to Einstein’s repulsive force, is not part of the matter tensor.
By rearrangement of Equation (11) one can set Λ on the right-hand side and thus the cosmological constant appears as an additional matter tensor,

And hence we have,
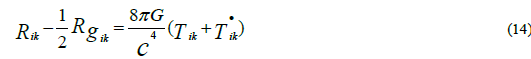
The matter term in Equation (14) consists of two different sources of energy: the term Tik, which represents the gravitational energy
of the baryonic matter, and a repulsive term 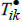 the excitation energy of the quantum vacuum that is represented by the energy of
photons. Thus, when applied to the universe as a whole, the Friedman solution of equation (14) obtains the following form:
the excitation energy of the quantum vacuum that is represented by the energy of
photons. Thus, when applied to the universe as a whole, the Friedman solution of equation (14) obtains the following form:
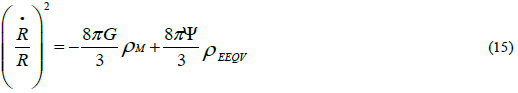
or in an equivalent representation,
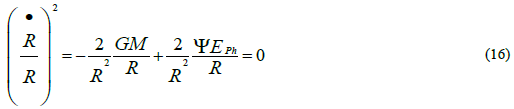
The first term on the right-hand side of Equation (15) is Einstein’s matter tensor. The second term is a new repulsive term; the excitation energy of the quantum vacuum above the ground energy state, expressed by the energy density of the CMB, ρPh, which is considered to be a property of space-time itself and consequently not part of the matter tensor. Ψ is a constant used to convert the total energy of the CMB into energy per unit mass. For a flat universe the numerical value of Ψ can be inferred from Equation (9) for every mass density ρM and the corresponding radius RU.
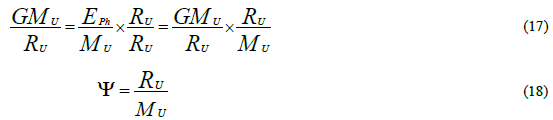
The results are shown in TABLE 3.
TABLE 3. Normalization factor Ψ for different matter densities.
| ρM×10-31g cm-3 | 1 | 1.7 | 2 | 3 | 4 | 5 |
| Ψ cm g-1 | 1.89E-22 | 2.70E-21 | 3.18E-21 | 4.77E-22 | 6.36E-21 | 7.94E-21 |
Equation (15) describes a flat, static universe in which the attractive (gravitational) and repulsive (EEQV) forces maintain an exact balance for every radius RU>RSch (where RSch is the Schwarzschild radius) suggesting a static universe.
For radii RU=RSch the gravitational potential (8πG/3)×ρM increases to c2 which is the maximum value allowed by GR and remains constant c2 for any radii RU<RSch. The repulsive force of the EEQV overwhelms the gravitational attraction, meaning that the universe becomes EEQV (radiation) dominated.

Physical Processes Occurring During the EEQV (Radiation) Dominated Era, Ru < Rsch
According to speculations regarding the emergence of the universe, the infant universe was an extremely hot, dense sphere of rapidly expanding radiation and some massless, relativistic particles and it began with zero baryon number. The physical processes occurring in this very early era of expansion are described by the Planck era, the grand unifying epoch and the inflationary epoch (if there was any inflation at all). About 1028 K the strong interaction becomes distinct from the electroweak interaction, and the universe expanded as assumed in the standard cosmology; it is sensible to start discussion at this temperature.
Quasi inflation and instantaneous isotropization of radiation simultaneously with the big bang event
Expanding universe models consider the universe to be homogeneous and isotropic on a large scale; however, this approach is physically incomplete. The incompleteness follows from the reasonable prediction that without fine-tuning of the initial conditions the Big Bang event must have produced regions with different radiation densities and temperatures, which were not in causal contact via either radiative or gravitative forces. Accordingly, the initial universe was neither homogeneous nor isotropic at the outset; rather, it must be considered as consisting of a large number of individual patches (approximated by spheres) with different radiation densities ρPh, each of which expanded independently according to their own energy density. From this it follows that according to Equation [16] regions with higher energy density must have expanded faster than regions with lower density, and this process is accompanied by prompt isotropization of primordial radiation. Setting 3/(2×t)=constant=1 in Equation (20), for equal expansion times t the redshift ratios for the different Hubble constants, H0=10, 15, 20 km s-1 Mpc-1, for example, can be inferred as 1: 0.832: 0.687

For H0=10, 15, 20 km s-1 Mpc-1 at the RS rations of 1: 0.832: 0.687 the expansion time (inferred from Equation (21)), the Hubble constant (inferred from Equation 22) and the critical mass density (inferred from Equation (23)) have the same value, regardless of whether the separate spheres are in causal contact or not.

The results are shown in TABLE 4 and TABLE 5.
TABLE 4. Cosmological parameter used for calculation.
| H0 kms-1 Mpc-1 | ρ0 kgm-3×10-28 | Ru cm | Mug | Ψ cmg-1 |
|---|---|---|---|---|
| 10 | 1.878 | 6.53E+32 | 2.19E+58 | 2.98E-21 |
| 15 | 4.226 | 2,90E+27 | 4.32E+57 | 6.72E-22 |
| 20 | 7.514 | 1.63E+32 | 1.37E+57 | 1.19E-20 |
TABLE 5. RS rations at the same expansion times, and Hubble constants and densities.
| H0 | z | Age universe at z, sec. | H(t) at z | ρ at z | ergs g-1 | Age universe | |
|---|---|---|---|---|---|---|---|
| Epoch | km s-1 Mpc-1 | at z, sec | km s-1 Mpc-1 | kg m-3 | at z=1090, sec | ||
| Isotropisation | 10 | 1,09E+28 | 1,8E-24 | 1.14E+46 | 2,46E+53 | 1.36E+47 | |
| 15 | 8,32E+27 | 1,8E-24 | 1.14E+46 | 2,46E+53 | 1.36E+47 | --- | |
| 20 | 6,87E+27 | 1,8E-24 | 1.14E+46 | 2,46E+53 | 1.36E+47 | ||
| Nucleosynthesis | 10 | 1,09E+10 | 5,7E+4 | 3,6E+14 | 2,46E-6 | 1.36E-10 | |
| 15 | 8,32E+9 | 5,7E+4 | 3,6E+14 | 2,46E-6 | 1,36E-10 | --- | |
| 20 | 6,87E+9 | 5,7E+4 | 3,6E+14 | 2,46E-6 | 1.36E-10 | ||
| Recombination | 10 | 1090 | 5,7E+13 | 3,6E+5 | 2,46E-22 | 1.36E-28 | 5,7E+13 |
| 15 | 832 | 5,7E+13 | 3,6E+5 | 2,46E-22 | 1.36E-28 | 3,8E+13 | |
| 20 | 687 | 5,7E+13 | 3,6E+5 | 2,46E-22 | 1.36E-28 | 2,85E+13 |
It can be seen from TABLE 5 that due to the high value of the Hubble variable H(t)=1.138×1043 km s-1 Mpc-1 at z=1.09×1028, for example, immediately after the BB the expansion is accompanied by a proceeding simultaneous and instantaneous leveling of the density fluctuations (occurring in a few quadrillionths of second). The energy distribution becomes isotropic and the universe consists of a number of spheres of different sizes; however, all the spheres have now equal expansion times, expansion velocities, gravitational potential and mass densities and this equality is preserved for the duration of the entire period of expansion.
Thermalization of the Isotropic Radiation
Following isotropization, thermalization of the primordial radiation can take place at any point of the henceforward isotropic universe, thereby creating the perfect black-body spectrum of the same temperature in all spheres. At redshifts 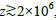 , effective thermalization mechanisms have been proposed that are capable of thermalizing almost any amount of radiation via Compton scattering, double compton emission and the up-scattering of photons to high frequencies [52, 53].
, effective thermalization mechanisms have been proposed that are capable of thermalizing almost any amount of radiation via Compton scattering, double compton emission and the up-scattering of photons to high frequencies [52, 53].
Primordial Big–Bang Nucleosynthesis
After about 10-6 sec. the universe cooled down to ~109 K and the BBN started. The most important parameters that allow for successful synthesis of the light elements H, D, He and Li are the photon-to-baryon ratio and the density of the baryonic matter. The accepted limits are NB/NPh=(2.5-6) ×10-10 corresponding to ρB=(1.7–4.1)×10-31 gcm-3. Because the critical density depends upon the Hubble constant, ρcrit=3H2/8πG, the contribution of the baryons to the critical density is constrained by the Hubble constant. When the universe is at its critical density, then, for h>0.2 nonbaryonic matter is required. Calculating BBN on basis of the presented model with h=0.126 and with ρB=3×10-31 g cm-3 leads to ΩBh2=0.0158, a value that is within the range of ΩBh2=0.01-0.025 in which nucleosynthesis can successfully take place without the need for DM.
The Cosmic Microwave Background
The next cosmological important event is the decoupling of the radiation of matter at z≈1090, thereby releasing the cosmic microwave background with remarkable properties. The CMB has perfect thermal blackbody spectrum with a temperature T0=2.725 K and minor local fluctuations from a perfect isotropy of δT/T=10-4. The question therefore arises as to how it is that different regions of the universe that were not in causal contact with each other following the BB can have the same temperature. In order to explain this cosmological conundrum, standard cosmology assumes that the uniformity of the radiation temperature should actually exist since the BB; however, this requires an extremely precise fine-tuning of the initial conditions. This is the horizon problem of standard cosmology.
Is the horizon problem a real problem at all?
Due to the isotropization of the radiation during the very first instant of expansion means that the horizon problem has astraightforward explanation: as discussed in previous sections, due to the individual expansion rates of each non-interacting sphere,there is a necessary leveling of the density fluctuations and this process takes place without the need for causal contact between thevarious non-interacting spheres. The universe becomes homogeneous without causal contact of the non-interacting spheres. Neitherthe presented model, nor the standard cosmological model requires inflation or fine tuning of the initial conditions, the answer tothe horizon problem is derived from the physics and mathematical interpretation of the expansion hypothesis itself.
Solution of the Flatness Problem
The area of the visible universe (CMB) shows no measurable curvature of space implying a flat universe. The flatness of the universe requires that the matter density and the kinetic energy of expansion must be fine-tuned in an order of magnitude of 1055:1. Within the frame of the PB model this outstanding puzzle in standard cosmology (i.e., the flatness or the fine-tuning problem) has a straightforward solution and no supernatural initial conditions are necessary to explain the fine tuning of the matter density ρM : H0 of 1:1055. Regardless of what the photon-to-baryon ratio was at the beginning, with decaying photon energy (increasing RU) the universe will automatically settle down at a radius RU=RSch to an exactly flat, static state with exact balance of the attractive and repulsive forces according to Equation (15) and hence the total energy of the universe will have zero net value. This result is also in agreement with the law of energy conservation which requires that the total energy in the universe, as measured by the space curvature, GMU/RU− ψEPh/RU, has zero net value.
Evolution of the Static Universe
The formally static universe as represented by Equation (16) is instable and underwent numerous structuring processes under the formation of huge voids with an extension of 100 Mpc and beyond. The three-dimensional distribution of luminous matters observed today has a soup bubble-like appearance with the galaxies located on the surface of the soup bubbles. Since voids are regions of suppressed gravity, the repulsive force of the EEQV overwhelms the gravitational attraction within the voids, and consequently the voids expand. Results indicate [39] that the universe expands with a velocity of h≈0.04 comparable to the expansion rate of the local void. The age of universe can therefore be inferred as ≈100 billion years, and galaxies can be formed in a regular way without the need for DM and/or DE.
Conclusions
The proposed PB model is based on the postulate that the universe can be described as an interacting attraction (gravitation)-repulsion (EEQV) system. Rather than presupposing repulsive scalar fields of unknown physical origin, I have introduced the excitation energy of the QV, expressed in terms of the energy density of the CMB, as a repulsive force. The basic parameters ρM and ρPh are determined from observations and not adjusted to the model and no free parameters are necessary. The model provides a straightforward explanation for the flatness and horizon problems without the need for DM and DE and without inflation or supernatural fine-tuning of the initial conditions. Flatness follows from the ratio of photons to baryons and this process is governed by microphysics and has nothing to do with the initial conditions.
The consideration of the separate development of gravitationally non-connected primordial density fluctuations immediately after the Big Bang and the rapid isotropization of radiation accompanying this process allows a subsequent thermalization of the radiation to a perfect Planckian-type energy distribution regardless whether or not the regions are in causal contact.
No funding was acquired for this research.
The author declares no conflicts of interest.
The author confirms that the data supporting the findings of this study are available within the article and the reference list.
References
- Sheldon E. Albert Einstein’s relativistic road ‘less traveled’ A review The road to relativity: the history and meaning of Einstein’s ‘The Foundation of General Relativity’, by Albert Einstein (Facsimile German Manuscript) and foreword by John Stachel, with annotations and commentary by Hanoch Gutfreund and Jürgen Renn. Contemp. Phys. 2016;57(2):250-4.
- Hubble E. A relation between distance and radial velocity among extra-galactic nebulae. Proceedings of the national academy of sciences. 1929;15(3):168-73.
- Albert Einstein’s relativistic road ‘less traveled’
- Friedmann, A. Über die Krümmung des Raumes. Zeitschrift für Physik. 1922;10, 377-86
- Guth AH. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D. 1981;23(2):347.
- Penrose R. Difficulties with inflationary cosmology. Annals of the New York Academy of Sciences. 1989;571:249-64.
- Steinhardt PJ. Is the theory at the heart of modern cosmology deeply awed?. Scientific American. 2011.
- Ijjas A, Steinhardt PJ, Loeb A. Inflationary paradigm in trouble after Planck2013. Phys. Lett. B. 2013;723(4-5):261-6.
- Turner MS, Weinberg EJ. Pre-big-bang inflation requires fine-tuning. Phys. Rev. D. 1997;56(8):4604.
- McCoy CD. Does inflation solve the hot big bang model׳ s fine-tuning problems?. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 2015;51:23-36.
- Freedman WL. Cosmology at crossroads: Tension with the Hubble constant. arXiv preprint arXiv:1706.02739. 2017.
- Mörtsell E, Dhawan S. Does the Hubble constant tension call for new physics?. J. Cosmol. Astropart. Phys. 2018;2018(09):025.
- Lineweaver CH, Barbosa D, Blanchard A, et al. Cosmic Microwave Background Observations: Implications for Hubble’s Constant and the Spectral Parameters n and Q. Astrophysics. 2008.
- Blanchard A, Douspis M, Rowan-Robinson M, et al. An alternative to the cosmological “concordance model”. Astron. Astrophys.2003;412(1):35-44.
- Marosi LA. Is the Velocity Interpretation of the Redshift of Spectral Lines in Accordance with Astronomical Data?. Int. J. Astron. Astrophys. 2017;7(4):248-54.
- Marosi LA. Hubble diagram test of 280 supernovae redshift data. J. Mod. Phys. 2014.
- Marosi LA. Modelling and Analysis of the Hubble Diagram of 280 Type SNIa Supernovae and Gamma Ray Bursts Redshifts with Analytical and Empirical Redshift/Magnitude Functions. Int. J. Astron. Astrophys.2016;6(3):272-5.
- Marosi LA. Extended Hubble diagram on the basis of gamma ray bursts including the high redshift range of z= 0.0331-8.1. Int. J. Astron. Astrophys. 2019;9(01):1.
- Vigoureux JM, Vigoureux D, Vigoureux P, et al. Analysis of the Hubble diagram of type SNe Ia supernovae and of gamma-ray bursts. A comparison between two models. arXiv preprint arXiv:1804.03519. 2018.
- Sandage A, Munch G, Mamaso A, et al. The universe at large. Key issues in astronomy and cosmology.
- Sandage A, Perelmuter JM. The surface brightness test for the expansion of the universe. II-Radii, surface brightness, and absolute magnitude correlations for nearby E galaxies. Astrophys. J. 1990;361:1-20.
- Sandage A, Lubin LM. The Tolman surface brightness test for the reality of the expansion. I. Calibration of the necessary local parameters. Astrophys. J. 2001;121(5):2271.
- Hubble E, Tolman RC. Two methods of investigating the nature of the nebular redshift. Astrophys. J. 1935;82:302.
- LaViolette PA. Is the universe really expanding?. Astrophys. J. 1986;301:544-53.
- Hartnett JG. Is the Universe really expanding?. arXiv preprint arXiv:1107.2485. 2011.
- Lerner EJ. Observations contradict galaxy size and surface brightness predictions that are based on the expanding universe hypothesis. Mon. Not. R. Astron. Soc. 2018;477(3):3185-96.
- Crawford DF. Observational evidence favors a static universe. arXiv preprint arXiv:1009.0953. 2010.
- Crawford DF. Is the universe static?. arXiv preprint arXiv:1804.10274. 2018.
- Orlov VV, Raikov AA. Cosmological tests and the evolution of extragalactic objects. Astron. Rep. 2016;60(5):477-85.
- La Violetta, Personal communication [Google Scholar] [Crossref]
- Brownstein JR, Moffat JW. Galaxy rotation curves without nonbaryonic dark matter. Astrophys. J.. 2006;636(2):721.
- Moffat JW. Modified gravitational theory as an alternative to dark energy and dark matter. arXiv preprint astro-ph/0403266. 2004.
- Moffat JW, Toth VT. Cosmological observations in a modified theory of gravity (MOG). Galaxies. 2013;1(1):65-82.
- Moffat JW, Toth VT. Observationally Verifiable Predictions of Modified Gravity. InAIP Conference Proceedings 2010;Vol. 1241, No. 1, pp. 1066-1073. Am. Inst. Phys.
- Milgrom M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983;270:365-70.
- Milgrom M. Does dark matter really exist?. Scientific American.2002;287(2):42-52.
- Rozgacheva IK, Agapov AA. Is Dark Matter Needed in Galaxies?. Astronomy Reports. 2018;62(9):551-6.
- Sivaram C, Arun K, Rebecca L. MOND, MONG, MORG as alternatives to dark matter and dark energy, and consequences for cosmic structures. J. Astrophys. Astron. 2020;41(1):1-6.
- Marosi LA. The Photon-Baryon Governed Universe. Phys. Res. Int. 2012.
- Marosi LA. Influence of the Soup-Bubble Structure on the Stability of a Static, Flat Universe Consisting of Matter and a Repulsive with 1/R Decaying Scalar Field. Apeiron: Studies in Infinite Nature. 2008;15(2).
- Moffat JW, Toth VT. Modified Gravity: Cosmology without dark matter or Einstein's cosmological constant. arXiv preprint arXiv:0710.0364. 2007.
- Bartlett JG, Blanchard A, Silk J, et al. The Case for a Hubble Constant of 30 km s–1 Mpc–1. Science. 1995;267(5200):980-3.
- Vigoureux JM, Vigoureux P, Vigoureux B. Cosmological applications of a geometrical interpretation of “c”. Int. J. Theor. Phys. 2008;47(4):928-35.,
- Maeder A. An alternative to the ΛCDM model: The case of scale invariance. Astrophys. J. 2017;834(2):194.
- Magain P. An expanding universe without dark matter and dark energy. arXiv preprint arXiv:1212.1110. 2012.
- Cole, K. C. Los Angeles Times: Data Back Einstein Theory of a Repelling Force, (Diskussion Riess, A., Krauss, L. and Kolb, R.) 1998.
- Krauss LM. Cosmological antigravity. Scientific American. 1999;280(1):52-9.
- Kraan-Korteweg RC, Lahav O. The universe behind the Milky Way. Astron. Astrophys. Rev. 2000;10(3):211-61.
- Peebles PJ, Ratra B. The cosmological constant and dark energy. Rev. mod. phys. 2003;75(2):559.
- Harrison, E. R. Cosmology: The Science of the Universe (Cambridge University Press). 1981
- Chluba J, Sunyaev RA. The evolution of CMB spectral distortions in the early Universe. Mon. Not. R. Astron. Soc. 2012;419(2):1294-314.
- Burigana C, De Zotti G, Danese L. Analytical description of spectral distortions of the cosmic microwave background. Astron. Astrophys. 1995;303:323.
- Landy, S. D. Mapping the universe, Scientific American. 1999; 280, 38-45

