Original Article

, Volume: 5( 4)

• View PDF
• Download PDF

Investigation of Stabilities and Instabilities at Tokamak Plasma Behaviour and Machine Learning with Big Data

*Correspondence:

Rastovic D Control Systems Group, Cetingradska, 10110 Zagreb, Croatia, Tel: +972 1-800-660-660; E-mail: dr.rastovic@excite.com

Abstract

We investigate the problem of stability and instability at tokamak plasma behaviour. Generally, Jaynes maximum entropy method and Bayesian decision can be applied for recognizing the shape of the plasma. In the case of the power law behaviour and the instabilities of plasma we introduce a new method. The maximization of mathematical expectations for events and fuzzy entropy is used for applications of fuzzy Bayesian neural networks for optimization and simulation without assumption on recurrence. In this case, it is possible to consider also the non-Gibbsian probability distribution functions with the power law case. The new calibration method for the non-equilibrium systems has been given.

Keywords

Stability; Instability; Tokamak; Bayesian learning

Introduction

Whether driven by magnetic or electrostatic turbulence, anomalous transport causes a large increase in the energy losses, and poses severe constraint on the amount of auxiliary power required to heat up the plasma to the high temperatures required for thermonuclear ignition.

The possible way to simulate the turbulence is given by a system of equations. We can consider all possible types of motions regular motion, Gaussian diffusion and Levy walk diffusion. At non-equilibrium systems the entropy can decrease with the step of the time.

Experimental Procedure

We introduce a new kind of entropy that is always monotonic and increasing as it is the case with the classical entropy for the equilibrium systems.

In many cases actual plasma are far from thermal equilibrium, being inhomogeneous or having non-Maxwellian velocity distributions, features which significantly complicate the analysis of experimental data.

Understanding and predicting turbulent transport is a key issue on the way toward commercially, viable fusion reactors. Indeed, turbulence controls the confinement control of any magnetically confined plasmas.

Externally applied, non-axisymmetric magnetic fields form the basis of several relatively simple and direct methods to control magnetohydrodynamic (MHD) instabilities in a tokamak, and most present and planned tokamaks now include a set of non-axisymmetric control coils for application of fields with low toroidal mode numbers. Saturated magnetic islands are manipulated directly with non-axisymmetric fields [1].

The properties of turbulence

Dynamical system can reach spontaneously a steady state exibiting some anologies with a thermodynamic system at a critical point. The system is driven to a stationary state where avalanches are distributed according to a power law. This phenomenon is called Self-Organized-Criticality (SOC) [2].

The development of fault diagnosis and sensor validation technique must face: the non-linearity of the process, the uncertain knowledge about the phenomena, often expressed in a linguistic fashion. The central problems are: plasma position, current and shape control.

The variational principle states that the entropy is maximal at equilibrium. There is no natural Gibbs distribution nor free energy in SOC system. It is not possible to analyze the out-of-equilibrium stationary state via a local equilibrium hypothesis where one decomposes the system into mesoscopic cells, locally at equilibrium.

Step-by-step new regimes of plasma operation have been identified, wherely turbulence can be externally controlled, which led to better and better confinement. Turbulence as a whole is not an equilibrium phenomenon. In the framework of mesoscopic non-equilibrium thermodynamics has been obtained a generalized Fokker-Planck equation, incorporating memory effects through time-dependent coefficients.

Anomalous transport has been found where turbulent processes of various kind are responsable for enhanced transport. Fluctuations are in many cases driven by nonlinear instability mechanisms, not by the linear instability mechanisms. Turbulent states do not satisfy the equipartition law. Therefore, even if plasmas are in thermodynamical equilibrium, the conventional statistical theory may not be sufficient. One formal way of the statistical theory is to extend the definition of entropy. We consider the fuzzy entropy.

For the most complicated cases of long interactions of the tokamak plasma, the approach with long memory effects can be applied via the theory of fuzzy neural Bayesian networks. The goal is, with localized control, to overcome the problems of non-equilibrium in plasma. In the case of stochastic turbulence, we define the fuzzy information entropy by:

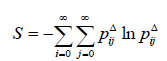(1)

where S is the spatiotemporal fuzzy Shannon Ent,.

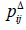is the fuzzy component that has a membership function.

As final criteria we take the maximal amount of mathematical expectations over the tree of events. Non-extensive statistical mechanics appears as a powerfull way to describe complex systems. With S(i) we shall denote for each time step i, the fuzzy spatial entropy:

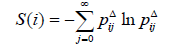(2)

Turbulent transport in tokamak is very challenging scientific problem. Our goal is to develop quantitative predictions of tokamak turbulence and to use them in design of future fusion reactors.

We can consider the control system of the linearized Vlasov-Poisson-Fokker-Planck equations:

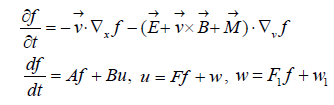(3)

Where A is,

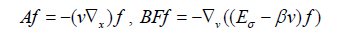
and

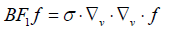(4)

E (t, x) is the force field acting on particles. The strictly positive parameters β and α model a certain type of interaction between particles. The control of plasma transport, laminar and turbulent has been investigated.

We have the optimal control of tokamak resistive wall mode in the presence of noise. The effect of the finitely conducting wall is to reduce the ideal mode to a slow growing resistive wall mode, which needs to be feedback stabilized for high performance. Instead of “state” feedback one may consider use of multiple independent simple single mode (N) controllers acting on spatially filtered several N modes. However, these are often coupled at tokamak.

We can introduce feature regularization during feature selection for value function approximation. The smoothness prior is effective in the feature selection setting and present closed form smoothness, regularizers for the Fourier base [3].

We have general formalism of optimal control. Optimal feedback design that is based on deterministic model, is minimization of total fluctuation energy of the instabilities, as well as minimization of control power:

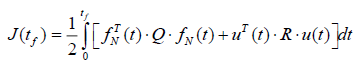(5)

For Lagrangian,

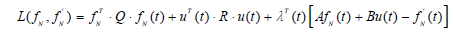(6)

It holds that, 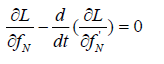(7)

with optimal control 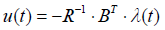(8)

which is easily obtained from Hamiltonian H. The Hamiltonian represents the total energy of the system, which is the sum of kinetic and potential energy. According to the Pontrjagin’s principle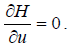

When a magnetically confined plasma is heated strongly and a threshold heating power level is exited, it may make spontaneously transition from a low-confinement (or L-mode) state to a high confinement (or H-mode) state. In the H-mode, the energy confinement time is significantly enhanced, i.e., typically by a factor of 2 or more. H-mode profiles have a characteristic edge pedestal. Improved confinement regime, or H-mode, first discovered by Fritz Wagner on ASDEX tokamak, is primarily due to the formation of an insulating region at the plasma edge, where step pressure gradients can form. A feature of H-mode operation is a series of explosive plasma events, called Edge Localized Modes or ELMs. There is the present understanding of these ELMs in terms of ideal magneto-hydrodynamic instabilities.

The magneto-hydrodynamic (MHD) stability of burning plasma is a key issue for operations of ITER. One key of MHD instability that can affected by alpha particles is the sawtooth oscilation. The prevention of core impurity accumulation is to apply neutral beam injection (NBI) heating in the opposite direction to the plasma current.

At the ASDEX tokamak experiment, a new feedback control loop is under construction with the aim of stabilizing MHD instabilities, such as neoclassical tearing modes and sawteeth. At the sawtooth behavior in the comiter – NBI regime is attributed to a subtle balance of the competing stabilization from the toroidal rotation and destabilization from the presence of energetic ions [4,5] Broadening the internal transport barriers can improve MHD stability.

Stochasticity of magnetic field lines is paramount to understanding particle transport and mixing. In the paper [6] is studied magnetic field separation in turbulent plasmas, which feature so-called super-diffusion, where field lines separate faster than diffusively.

The starting point of theoretical treatment of plasma confinement in tokamak is the equilibrium configuration. Any magnetic field that breaks the exact axisymmetric of the equilibrium tokamak field is a non-integrable perturbation [7]. The KAM (Kolmogorov-Arnold-Moser) theory predicts that, for those irrational surfaces with safety factors sufficiently far from rational m/n, the topology is preserved and the surfaces are only slightly deformed from the unperturbed tori (KAM surfaces). Similar effects can be obtained by the theory of Landau damping.

The equilibrium code solves the Grad-Shafranov equation:

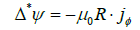(9)

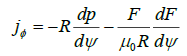(10)

where Ψ is the poloidal flux function, j_φ is the toroidal current density, p is the pressure, and F = RB_φ is the toroidal field function.

The “standard model “ of classical plasma physics is the Vlasov-Poisson-Fokker-Planck equation, here written with periodic boundary conditions and in dimensionless units:

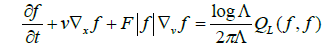(11)

where f=f (t, x, v) is the electron distribution function.

The nonlinear Landau damping for general interactions has been obtained by Mouhot and Villani [8]. The unique solution of the nonlinear Vlasov equation satisfies:

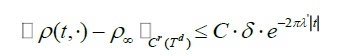(12)

where 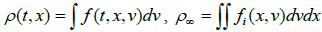(13)

Again, here we have some kind of exponential behavior.

Let us consider fuzzy entropy for controlled fuzzy stochastic process:

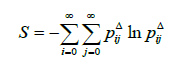(14)

enerally, even for non-equilibrium systems, the maximum of fuzzy entropy should be obtained without techniques of Jaynes’ constraints, with Bayesian learning rules for infinite fuzzy logic controller,

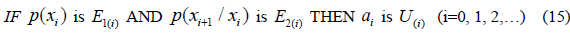[9].

The goal is, with localized control, overcome the problem of non-equilibrium in plasma. The aim is converting the anomalous diffusion to the exponentially stabilizable diffusion, when it is possible [10].

The Monte Carlo algorithm we are concerned with can be understood as a numerical method of solving the drift kinetic equation. Fuzzy probability theory, a theory in the process of development, is just standard probability theory with the generalized concept of random variables.

More investigations are needed to establish the nature of instabilities and driving mechanism involved. For a detailed analysis of turbulence, adequate analysis tools are required. In the core of tokamak plasmas, the turbulence is believed to govern transport processes.

It is shown that for some cases, the control system of the linearized transport equation with a controllable unstable part is exponentially stabilizable [11] As generalization, the asymptotic stability of a certain class of integrated semigroups is discussed by means of Lyapunov functionals [12]. In this case, we obtain the exponentially bounded behavior in the sense that,

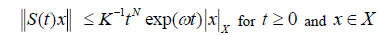(where K denotes n factorial) (16)

The possible interconnection between of the equilibrium and of the anomalous transport has been discussed.

A nice example of construction of fuzzy probabilistic distribution and the fuzzy entropy has been given in [13].

There is a method for solving the Fokker-Planck equation in tokamak plasmas [14]. The code provides a set of powerful tools for studying radio frequency wave heating and current drive in tokamak plasmas.

Results and Discussion

Fuzzy Bayesian computation

Approximate Bayesian Computation is a family of computational techniques which offer an almost automated solution in situations where evaluation of the posterior likelihood is computationally prohibitive or whenever suitable likelihoods are not available [15]. We consider the fuzzy Bayesian computation. The basic idea is that using a representative enough summary statistic coupled with a small enough tolerance level ε should produce a good approximation of the posterior distribution. Power laws are well known from the work by Pareto for the distribution of income. For example (short-time) particle travel behavior can be well described by a decreasing power law of distance x, that is, 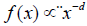with positive decay parameter d. An important characteristic of this power law is its slow convergence to zero, which in application enables long-range actions in addition to principal short-range actions. They describe the distribution of earthquake magnitudes and many other natural phenomena. An alternative spatial interaction function of an isotropic Gaussian kernel 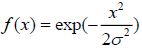with scale parameter σ allows for occasional long-range actions: a power law. The shifted version known as Pareto type II has density kernel 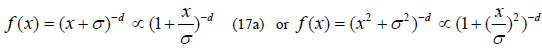(17b) Extreme learning machine (ELM) is a new approach for learning the parameters of the hidden layers of a multilayer neural network (as a multilayer perceptron or the radial basis function neural network). Its main advantage is the lower computational cost. The research on Bayesian methods for neural models has become very intense currently. These methods introduce a probability distribution on the network parameters and the committed errors. The Bayesian ELM has the advantages of both ELM and Bayesian models [16]. Bayesian linear regression is optimizing the weights of the output layer.

Any Bayesian modeling is carried out in two steps:

1. Inference of the posterior distribution

2. Calculation of the output distribution

The Bayesian approach involves the use of some parameters (hyper-parameters) that allow regularization. The use of confidence intervals increases the reliability of a model’s output. A priori knowledge can be introduced in the models by means of error distribution and parameter distributions that must be defined when applying Bayes’ theorem. This knowledge can improve the performance of the model.

Normal distributions emerge naturally when formulating a central limit theorem, as solution of linear Fokker-Planck (FP) equations. Similarly, q-Gaussian distributions are related to generalized central limit theorem, are solutions of a kind of nonlinear FP equations and maximize non-extensive Tsallis entropy and a generalized second order moment constraints to obtain oscillatory behavior. There is the equivalent formulation of such phenomena inside of the theory of fuzzy Jaynes entropy.

Fuzzy controlled Markovian process can be obtained from general non-Markovian stochastic process via artificial fuzzy neural networks in some cases. Many current models for long-memory are non-Markovian. The turbulent flux constitutes a random process with significant deviations from Gaussian statistics. Detailed information concerning the turbulent fluxes can be obtained by conditioned averaging.

We understood entropy as a measure of uncertainity of Markov process. The “uncertainity of uncertainity” is unavoidable in non-equilibrium systems. It is the case which is obtained by fuzzy entropy. For controlled fuzzy Markov chain we use the following infinite fuzzy logic controller with Bayesian learning rules:

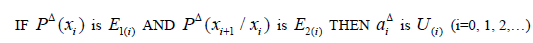(17)

As “defuzzification“ on 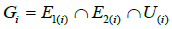we can take the following reason: the actions 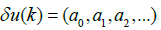(18) are given on such a way that the maximum of information fuzzy entropy 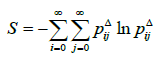is obtained, where 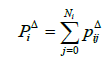is possible uncertain clustering, for global optimization in time domain [17].

For actions ai we can take fuzzy neural network to memorize the past (history) at given moment i.

For times longer than the relaxation times, the correlation function for anomalous diffusion becomes a power law for broadband noise. Anomalous transport to be induced by the plasma turbulence caused various instabilities. In the fusion-related research using toroidal plasmas, the suppression of turbulence has been main problem to make confinement time longer. Two major challenges remain in clustering methods. One is efficient sampling. The other major challenge is posterior inference.

We can use Bayesian inference.

Let us consider an ill-posed inverse problem where a physical quantity needs to be recovered from an indirect measurement modeled by 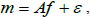where ε is white noise taking values in R^k.

In Bayesian inversion, the quantities m_n , f_(n) and ε where ε is white noise, taking values in R^k These quantities are considering as random variables. We use the fuzzy Bayes formula:

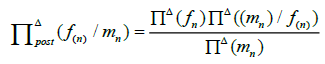(19)

Given a realization 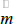, after appropriate defuzzification, the maximum a posteriori estimate 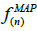defined by:

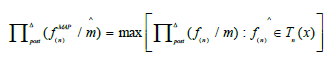(20)

The Bayesian inversion generalizes deterministic regularization and yields information about the structure of ill posed inverse problem.

The plasma evolution solver involves more physics of uncertainity than the equilibrium solver [18].

The aim was to obtain the maximum of information fuzzy entropy by fuzzy Bayesian rules, that generalizes the Jaynes method for equilibriums [19] to the case of non-equilibriums.

In a tokamak reactor, several magnetic fields have to be applied to confine the plasma. These are combined toroidal and poloidal magnetic fields. They are necessary to both: achieve the desired plasma configuration and to control the plasma shape and position [20].

With the methods of artificial neural networks with back-propagation it is possible recognize the solutions of Grad-Shafranov equations [21].

Conclusion

We have described how to determine the optimal a posteriori probability distribution and the appropriate actions. Examples of particularly popular estimation approaches include regularized variants of the Expectation-Maximization algorithm. We have explored the effects of specifying white noise (no memory), autoregressive (short memory) and long-memory correlation structures for error processes. The prior level allows for Bayesian inference by providing prior distributions for all unknown parameters in the data-and process-levels [22].

The Bayesian,modeling framework is closely related to the stochastic filtering methods, for example classical Kalman filtering.

The Bayesian approach allows for all parameters to be estimated while avoiding the known estimation difficulties inherent to filtering. When estimating the spline coefficients, no information on levels or trends during the observation period was exchanged if it was possible [23]. In the case of changes in plasma evolution it has been shown that with Bayesian learning and maximum of fuzzy entropy can be reached all probabilistic distributions, including non-Gibbsians distributions [24,25].

References

1. Strait EJ. Magnetic control of magnetohydrodynamic instabilities in tokamaks. Phys Plasmas. 2015;22:21803.
2. Cessac B, Blanchard PH, Kruger T, et al. Self-organized criticality and thermodynamic formalism. Jrl of Stat Phys. 2004;115:1283-326.
3. Wookey DS, Konidaris GD. Regularized feature selection in reinforcement learning. Mach Learn. 2015;100:655-676.
4. Sen AK, Nagashima M, Longman RW. Optimal control of Tokamak resistive wall modes in the presence of noise. Phys Plasmas. 2003;10:4350.
5. Rastovic D. Fuzzy scaling and stability of tokamaks. J Fusion Energy. 2009;28:101-6.
6. Beresnyak A. Asymmetric diffusion of magnetic field lines in turbulence. Phys Scr. 2014;89:118001.
7. Garabedian PR. A unified theory of tokamaks and stellarators. Comm Pure Appl Math. 1994;47:281-292.
8. Mouhot C, Villani C. Landau damping. J Math Phys. 2010;51:015204.
9. Rastovic D. Targeting and synchronization of tokamak with recurrent artificial neural networks. J Neural Comp & Appl. 2012;21:1065-69.
10. Rastovic D. On stochastic control of tokamak and artificial intelligence. J Fusion Energy. 2007;26:337-42.
11. Rastovic D. Feedback stabilization of some classes of nonlinear transport systems. Rend Circ Mat Palermo. 2002; 51:325-32.
12. Rastovic D. A note on stability properties of integrated semigroups. Acta Math Inf Univ. Ostraviensis. 1995;3:61-65.
13. Kaufmann A. Introduction to the Theory of Fuzzy Subsets. Academic Press Inc. New York. 1975.
14. Zheng P. Fully implicit iterative solving method for the Fokker-Planck equation in tokamak plasmas. Plasma Sci Technol. 2014;16:1000-9.
15. Biau G, Cerou F, Guyader A. New insights into approximate Bayesian computation. Annal Inst Henri Poincare. 2015;51:376-403.
16. E Soria-Olivas. BELM: Bayesian Extreme Learning Machine. IEEE Trans. Neural Networks. 2011;22:505-510.
17. Rastovic D. From non-Markovian processes to Stochastic real time control for Tokamak plasma turbulence via artificial intelligence techniques. J Fusion Energy. 2015;34:207-215.
18. Morabito FC. Equilibrium parameters recovery for experimental data in ASDEX upgrade elongated plasmas, Neural Networks. Proc IEEE Int Conf. 1995;27.
19. Rastovic D. Infinite fuzzy logic controller and maximum entropy principle. InterStat. Virginia. 2003.
20. Ambrosino G. Plasma vertical stabilization in the ITER tokamak via constrained static output feedback. IEEEE Trans Control Systems Technology. 2011;19:376-389.
21. Lister JB, Schnurrenberger H. Fast non-linear extraction of plasma equilibrium parameters using a neural network mapping. Nucl Fusion. 1991;31:1291-1300.
22. Dong Li, Yi Liu, Svensson J, et al. Bayesian soft x-ray tomography and MHD mode analysis on HL-2A. Nucl Fusion. 2016;56:036012.
23. Rastovic D. Approach with different entropies to the problem of plasma confinement. Journal of Physics & Astronomy. 2016;4:1-5.
24. Rastovic D. Physics electronics and entropies for plasma confinement. Journal of Physics & Astronomy. 2013;2:75-80.
25. Rastovic D. Tokamak design as one sustainable system. Neural Network World. 2011;6:493-504.