Short communication
, Volume: 6( 2)Who Invented the Mass-Energy Equivalence Principle
Received: June 01, 2018; Accepted: June 07, 2018; Published: June 14, 2018
Citation: Főfai S. Who Invented the Mass-Energy Equivalence Principle. J Phys Astron. 2018; 6(2):157
Abstract
The most famous equation in the world is probably the one defining the relation between mass and energy. Every student attending secondary grammar schools knows it, and names Albert Einstein, as its inventor, adding that the equation is the result of Einstein’s Special Relativity Theory. However problems arise when the simply equation should be derived with Lorentz’s factor according to Special Relativity, because the factor has no upper limit when the velocity of a mass (v) nears the speed of light (c), while E=mc2 has definite value. Only a few knew, that the story of mass-energy equivalence, began with Newton in 1704, and the famous equation was derived with classical, Newtonian method in the 19th century, well before Special Relativity was created.
Keywords
Mass; Energy; Relativity theory
Introduction
Light-material interaction, mass-energy equivalence as it began
In 1704 Sir Isaac Newton wrote in his book “Opticks” [1]:
“Do not Bodies and Light act mutually upon one another that is to say, Bodies upon Light in emitting, reflecting, refracting and inflecting it, and Light upon Bodies for heating them, and putting their parts into a vibrating motion wherein heat consists?”
"Gross bodies and light are convertible into one another...",
With this words Newton created the mass-energy equivalence principle, which urged later scientists to find mathematical solutions for his logical hypothesis.
Mass – Energy Transformation
In 1873 Nikolay Umov a Russian physicist and mathematician created an equation for mass energy transformation [2]:
E=kmc2 where 0,5 ≤ k ≤ 1
We can calculate the transformation too by using the equation of kinetic energy: E=½mv2
Let’s presume a photon leaves an object with the speed of light, decreasing the mass at the same time:
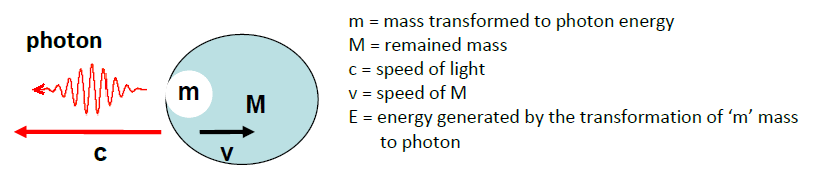
Total energy of transformation: E = mc2 /2+ Mv2/2
If M →m then v → c and E→ mc2 ;
If m << M then v → 0 and E →mc2 /2;
so E = kmc2 where 0,5 ≤ k ≤ 1
We got the equation of Umov. It can be seen, that when all the mass turns into Energy then k=1 and E= mc2.
Because nobody before Umov published this equation he is the real inventor of the E=mc2 formula.
In 1900 H. Poincare and in 1903 Olinto de Pretto concluded too, that the relation between energy and mass is E=mc2. Notice, that the equation of E=mc2 is a classical Newtonian relation in this context.
The Relativistic Interpretation of E=mc2
In 1905 Albert Einstein claimed that E = mc2 is a consequence of his Special Relativity Theory.
However the relativistic values of energy, mass and momentum have no upper limit, because of Lorentz’s factor used in Special Relativity Theory:
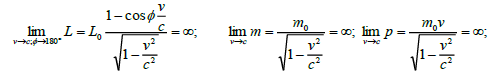
where: L=Light Energy (used by Einstein [3] ), ф=angle of movement,
p = relativistic momentum, m = relativistic mass, m0 = mass in rest.
Many accuse Einstein with plagiarism on account of his claim, because the equation of E=mc2 existed earlier. However it can be seen, that the relativistic interpretation equals with the classical equation multiplied by Lorentz’s factor, so Einstein modified the earlier formula:
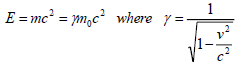
where: E = relativistic energy, m = relativistic mass,
m0 = mass in rest, γ = Lorentz’s factor.
Discussion
In fact there is a classical equation of mass-energy equivalence: E=mc2 invented first by Nikolay Umov and there is a relativistic equation: E= γmc2 created by Einstein, (where m=mass in rest). The problem is that that the classical equation is interpreted as the relativistic one invented by Einstein, despite the fact, that it cannot be derived with Lorentz’s factor. The usage of the two equations isn’t separated either, generally the classic one is used or referred to. Although there is a significant difference between the two equations, their status hasn’t been settled yet.
Example:
Let’s presume that a 1kg object travels with 290 000 km/s velocity. Calculating the energy of its mass, we get different results with relativistic and classic methods. mass m0=1kg; velocity of mass v= 290 000 000 m/s; Speed of light = 300 000 000 m/s
Classical energy of mass: E=m0c2 = 9 × 1016J
Relativistic mass m = γm0 = 3,9 kg
Relativistic energy of mass at 290 000 km/s: E=mc2 = 3,5 x 1017 J that is 3,9 times of the classical Energy.
Nearing the speed of light, the relativistic mass, momentum and energy are increasing limitless.
Relativistic energy of mass: when v → c then E= γmc2→∞
References
- Isaac NS. Opticks, Dover Publications, Inc., New York, p. CVX. 1704.
- Mass - Energy equivalence.
- Einstein, W, A Ann. Physik.1905;18:639.

